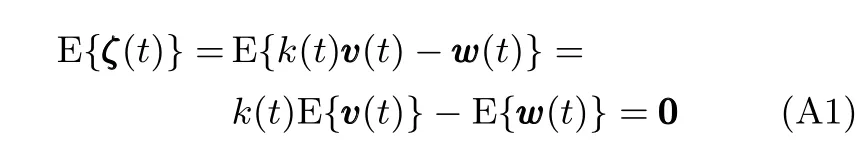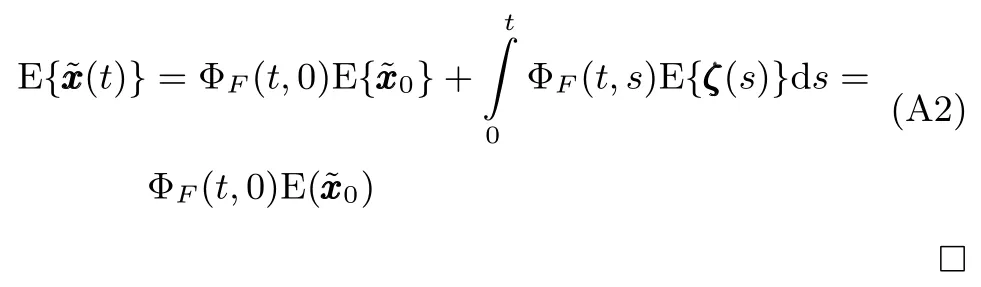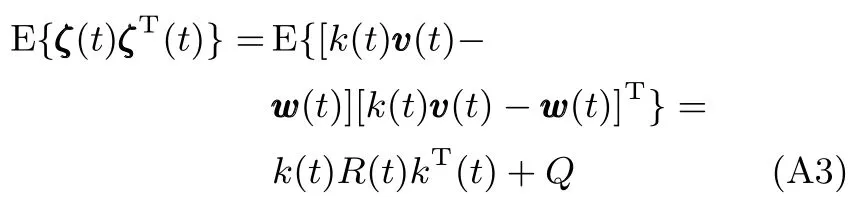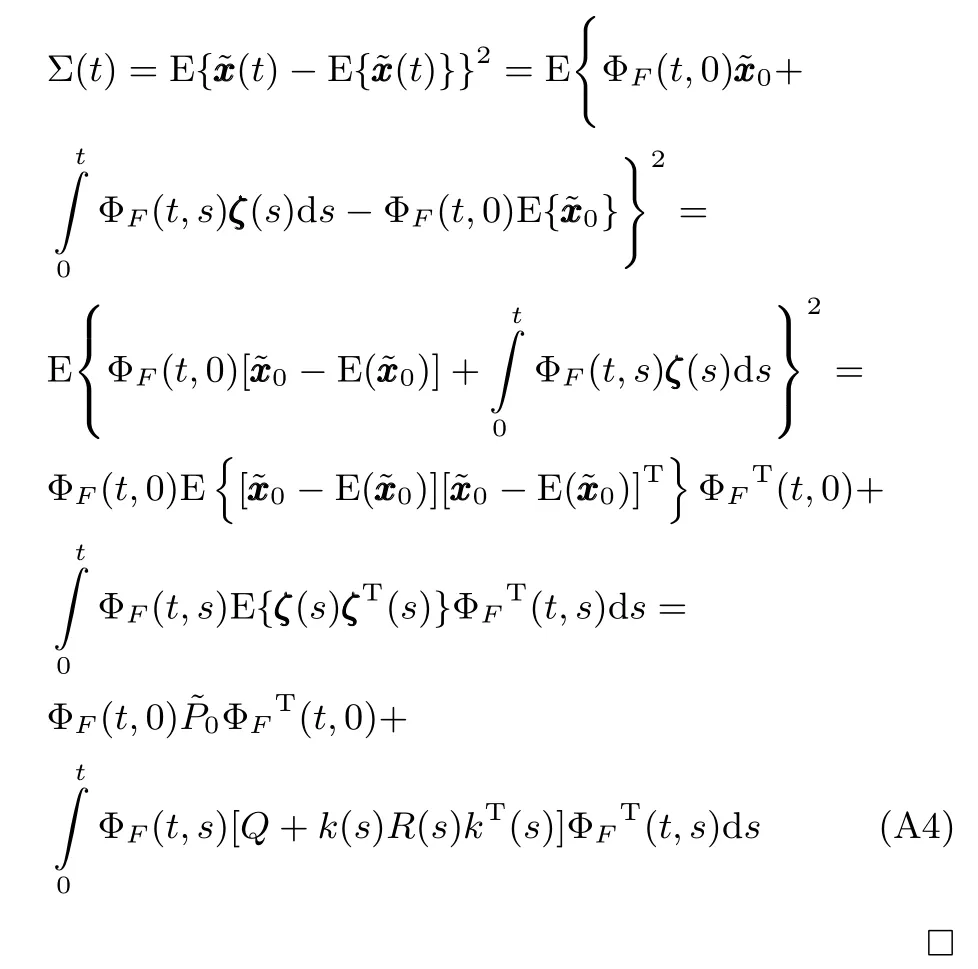模式失配条件下连续时间控制系统的零控脱靶量估计误差分布
项盛文 范红旗 付强
海湾战争以后,战术弹道导弹(Tactical ballistic missiles,TBM)逐渐成为防空系统的拦截对象,而具有潜在机动能力的TBM 的出现,则给现有防空系统提出严峻的挑战.当前,高速大机动目标拦截问题引起了国内外各研究团队的广泛关注,其中最具代表的是以色列的Shinar团队[1−4].此类目标拦截的最大挑战在于它要求特别小的脱靶量(Miss distance,MD)甚至是直接碰撞.对于该问题,由于导弹加速度饱和、非高斯噪声以及系统的非线性,确定性等价原理[5]已不再适用.然而,当导弹和目标的相对状态满足可观测性条件时,部分分离定理仍然成立,此时估计器仍可独立于导引律进行设计[6].
在估计器给定后,建立零控脱靶量(Zero-effort miss distance,ZEM)的估计误差模型便具有重要意义.一方面,ZEM是导引律中的一项关键输入参数,不同导引律间的区别仅在于不同的ZEM 计算方式.因此,ZEM的估计精度将直接影响制导性能,合适的ZEM估计误差模型可以有效指导制导系统的设计.另一方面,作为评价高度大机动目标拦截性能的重要指标,脱靶量的解析计算方法中需要用到ZEM的估计误差模型[7−10].
目前,在给定系统动态模型、估计器、控制策略、以及具体的扰动和噪声模型后,ZEM 的估计误差分布主要通过大量蒙特卡洛仿真得到.然而,这种后验方法在控制系统设计阶段并不十分适用.Moldavskaya等[11]提出了一种求解ZEM 估计误差分布的解析方法.采用成形滤波器技术近似目标加速度指令,近似的指令由白噪声通过一个一阶线性系统后得到,且与原指令具有相同的自相关函数.假定初始的估计误差为零,测量噪声和状态噪声为互相独立的零均值高斯白噪声,则得出ZEM 的估计误差服从零均值高斯分布,其中状态估计误差的方差矩阵满足Riccati方程.
在末制导系统中,由于系统误差、观测噪声等不确定因素以及不完全的状态观测,估计器需同时扮演观测器和滤波器的角色,即要求其同时兼顾未知状态重建及测量噪声滤波这两方面的性能,但使用固定带宽的成形滤波器难以同时兼顾估计精度和响应速度.相关的研究工作表明,组合使用独立模式辨识器和一个低带宽高精度估计器更适合高速大机动目标的拦截问题,可显著提升制导性能[12−14].实际上,对于高速大机动目标拦截,雷达和光电导引头能够观测到目标的特征信息,这些特征为模式辨识器的设计提供了额外的信息且可改善系统对目标机动的响应速度[15−18].Fan等在引入独立模式辨识器的基础上,分析了状态估计的误差特性[19].考虑到ZEM对大机动目标拦截的重要意义,本文在此基础上推导模式失配条件下ZEM的估计误差分布.
1 问题描述
1.1 系统运动模型
与大多数机动目标拦截文献类似[7−11,20],本文仅考虑一弹一目的平面拦截情形.如图1所示,用P和E分别表示导弹(追方)和目标(逃方),并作如下假设[11,19−21]:
1)P和E的控制动态可用一阶转移函数来近似,相应的时间常数分别为τp和τe;
2)P和E的速度是恒定的,分别用Vp和Ve表示;
3)P和E的横向加速度有界,其最大横向加速度分别用表示.
在图1中,X轴沿弹目初始视线方向;Y垂直于X轴;(xp,yp)和(xe,ye)分别为P和E的当前坐标;φi,i=p,e分别是P和E的偏航角,它表示速度矢量和X轴的夹角.假设偏航角满足(sinφp=φp,sinφe=π − φe),则弹目运动轨迹可以沿着初始视线进行线性化.假定接近速度恒定,起始时刻t0=0s,给定弹目起始距离r0后,拦截的终止时刻满足:

剩余飞行时间定义为tgo=tf−t.
定义状态矢量x= [x1,x2,x3,x4]T=[y,y˙,aey,apy]T.基于上述三条假定,整个拦截过程的时间t∈[0,tf],且具有下述线性动态模型:
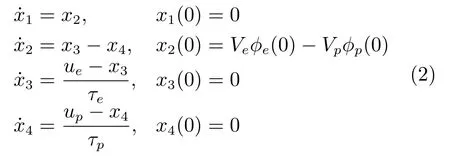
其中,x1=ye−yp为P和E之间沿Y轴的相对距离;x2为相对的横向速度;aiy,ui,i=p,e分别为i的横向加速度和加速度指令且满足:

定义

其中,γ称为机动过载比,ε通常称为敏捷系数.为了保证较好的拦截精度,传统最优控制框架下的导引律如OGL(Optimal guidance law)通常需要过载优势满足γ>3,比例导引和增广比例导引则需要4到5倍的过载优势,本文面向TBM拦截应用,考虑过载比γ<2.5的大机动目标且ε≈1.

图1 平面拦截几何Fig.1 Planer interception geometry
将动态模型写成矢量形式

其中

对状态方程(6)采用终端投影变换
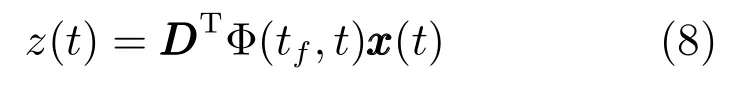
则可将平面拦截问题转换为一个标量问题.系统的新状态变量为零控脱靶量z(t),而系统的脱靶量则为终止时刻tf的z(t),即z(tf).式(8)中,D=[1,0,0,0]T;Φ(tf,t)为满足齐次方程的状态转移矩阵,求解得到:

因此,可将零控脱靶量z(t)表示为


1.2 马尔科夫跳变的加速度指令模型
与采用成形滤波器不同,本文引入一个独立的模式辨识器,采用马尔科夫跳变模型来描述目标的横向加速度控制指令:
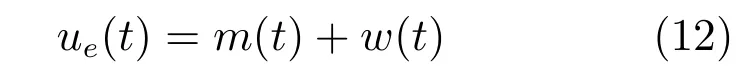
如图2所示,这里将目标横向加速度指令所在的控制空间量化为一系列离散点构成的模式集.假定:ue(t)在这些点之间跳变;m(t)为离散化的目标横向加速度指令,即目标的运动模式;w(t)为量化误差,假定其为零均值的高斯白噪声,功率谱密度为sw.有关机动目标跟踪模型集的设计方法可以参见文献[15,22−24].

图2 目标横向加速度指令模型集Fig.2 Mode-set of the evader's lateral acceleration command
不失一般性,假定[0,tf]内目标只发生一次模式切换,令tsw表示模式切换时刻,m1,m2分别表示模式切换前后目标的运动模式量,则m(t)可表示为
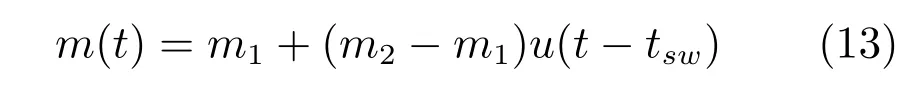
其中,u(t)为阶跃函数,定义为

1.3 系统观测模型
与文献[19]类似,本文采用的观测模型为
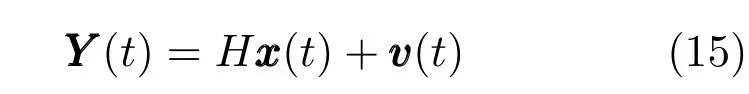
其中观测矩阵
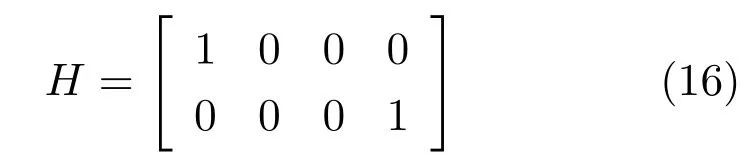
观测噪声v(t)为零均值的高斯白噪声,其协方差矩阵为R(t).
2 ZEM估计误差模型的推导
考虑如图3所示的一种典型的制导系统结构.图3中,独立的模式辨识器为估计器和导引律的设计提供目标的运动模式信息.文献[14]基于该架构给出的导引律为基于逻辑的联合估计导引律.本文在这个框架下推导模式失配条件下ZEM的估计误差分布形式.
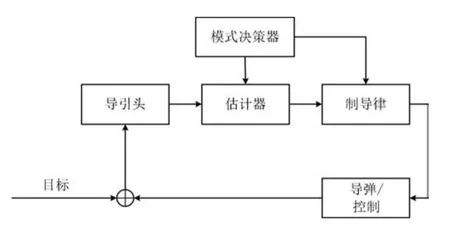
图3 一种典型的制导系统结构Fig.3 A typical structure of guidance system
在此,我们对模式辨识器的行为作如下假定:目标运动模式切换后经过∆t的时间延迟,模式辨识器可给出正确的模式估计结果.目标模式切换和模式辨识器的模式决策过程如图4所示.

图4 模式切换和模式辨识器输出示意图Fig.4 Diagram of mode switch and decision-maker output
将式(12)的目标加速度指令代入系统状态方程,可以得到:

估计器采用Kalman滤波器,由图4可知估计器的动态方程为
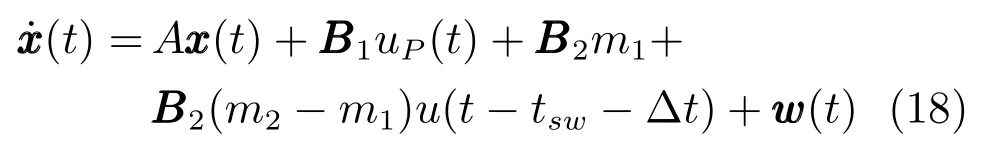
下面分三种情况讨论:
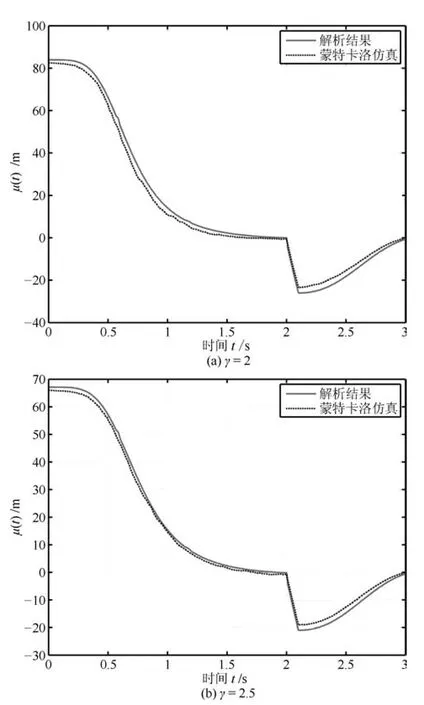
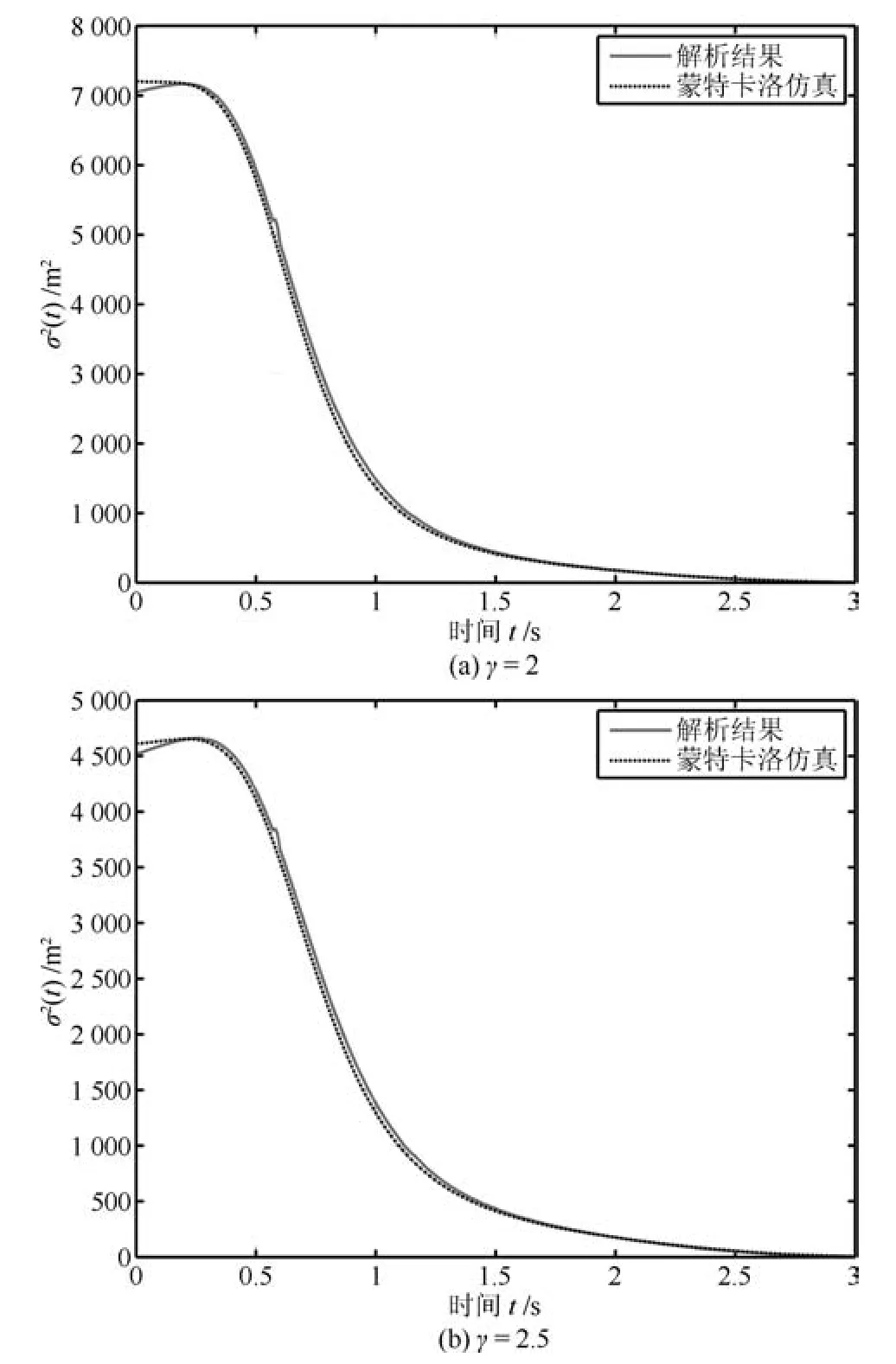
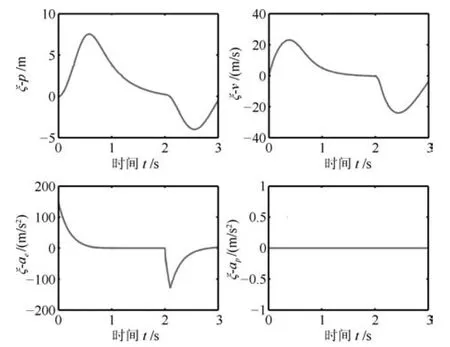
情形1.tf 结合式(15)观测模型可以得到下述滤波方程 其中,k(t)为系统的连续Kalman增益矩阵且满足 P(t)为预测误差的协方差矩阵,满足下述Riccati方程 情形2.tsw≤tf 1)t∈[0,tsw),此时估计器一直保持正确的模式,状态估计误差的均值和方差矩阵分别如式(25)和(26)所示. 2)t∈[tsw,tf],此时存在模式失配,系统的状态方程为 估计器的滤波方程仍为式(20).根据定义,可以得到状态估计误差的时间传递方程: 求解方程(28)得到 利用式(24)可得: 将其代入式(29),则 根据定义,状态估计误差的均值为 状态估计误差的方差矩阵同式(26).详细的推导过程见附录A. 情形3.tsw+∆t≤tf.需要分三段进行讨论: 1)t∈[0,tsw),此时系统的状态方程和估计器的滤波方程分别如式(19)和(20)所示,状态估计误差的均值和方差矩阵则分别见式(25)和(26). 2)t∈[tsw,tsw+∆t),存在模式失配,此时系统的状态方程和估计器的滤波方程分别如式(27)和(20)所示,状态估计误差的均值和方差则矩阵分别见式(32)和(26). 3)t∈[tsw+∆t,tf],估计器回到正确的目标模式上,此时的系统状态方程为式(27),而估计器的滤波方程为 根据定义,可以得到状态估计误差满足方程 求解得到 由式(31)可得: 代入式(35)后得到 根据定义,状态估计误差的均值为 状态估计误差的方差矩阵满足式(26),详细推导见附录A. 其中,ψ(θ)=exp(−θ)+θ−1. 因此,存在模式失配时每一时刻ZEM 的估计误差均服从有偏的高斯分布,其均值和方差分别为µ(t)和σ2(t).从式(40)和(41)的结果来看: 1)制导系统对ZEM估计误差的的影响主要体现在导引律、弹目时间常数、剩余飞行时间tgo以及观测精度4个方面;目标的影响则主要体现由机动导致的模式失配上. 2)模式失配只影响ZEM估计误差的均值µ(t),对σ2(t)没影响. 3)µ(t)和σ2(t)与系统所用的导引律无关,在后面的仿真验证中,不失一般性,导引律选用DGL/1. 4)tgo的估计精度及弹目时间常数τe和τp通过投影向量g(t)影响脱靶量.在具体的拦截问题中,弹目时间常数通常可假定为确定已知的,而雷达导引头可直接获得高精度的tgo测量,因此本文分析中不考虑它们对ZEM估计误差的影响. 5)估计器的观测精度将直接影响到Kalman增益系数k(t),见式(21),进而影响ZEM估计误差的均值和方差. 本节通过一个典型的TBM拦截场景验证前面理论推导的正确性,仿真参数设置如表1,蒙特卡洛仿真次数设置为1000. 表1 仿真参数Table 1 Simulation parameters 图5给出了两种不同过载比γ=2和γ=2.5下ZEM估计误差的均值变化曲线.从实验结果可以看出,本文推导的理论结果与蒙特卡洛仿真的曲线基本吻合.由图5还可以看出,当目标的运动模式改变时(t=2s),ZEM的估计误差会迅速增大,当运动模式被正确识别后(t=2.1s),ZEM的估计误差将逐渐减小.图6给出了这两种情形下ZEM估计误差的方差分布,可以看出本文理论推导结果与蒙特卡洛仿真的曲线同样也是吻合的.图5和图6的仿真结果充分说明了本文理论推导的正确性. 图5 ZEM估计误差的均值Fig.5 Mean of ZEM estimation error 图7给出了各状态分量的估计误差.由该图可见,当目标运动模式改变后,各状态分量的估计误差都迅速增大,当模式匹配后,估计误差逐渐减小;导弹自身加速度估计误差分量不受模式失配的影响,这与导弹自身的加速度模型是完美可知且可精确测量的假设相一致. 图6 ZEM估计误差的方差Fig.6 Variance of ZEM estimation error 图7 各状态估计误差Fig.7 Estimation error of every state 本文针对高速大机动目标拦截问题,推导了模式失配条件下ZEM估计误差的分布形式.在过程噪声和测量噪声均为零均值高斯白噪声且相互独立的假定下,每一时刻ZEM 的估计误差服从有偏的高斯分布.本文得到了各时刻ZEM估计误差均值和方差的解析表达式,并与蒙特卡洛仿真实验进行了对比,验证了理论推导的正确性. 将本文的ZEM估计误差模型应用于模式失配条件下脱靶量模型的推导,以及研究基于特征辅助的目标运动模式辨识算法将是下一步工作的方向. 附录A 情形1中ξ(t)和Σ(t)形式证明: 因为 所以 同理,很容易推出式(32)和(38),这里不再赘述. 同理,很容易得出在情形2和情形3下,Σ(t)的表达式与式(26)相同,这里不再赘述. 附录B
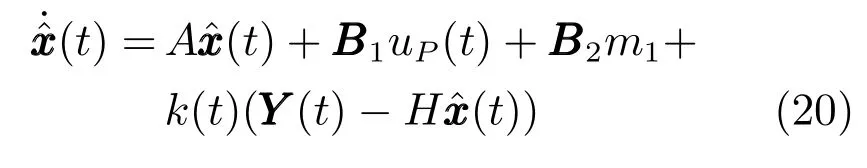







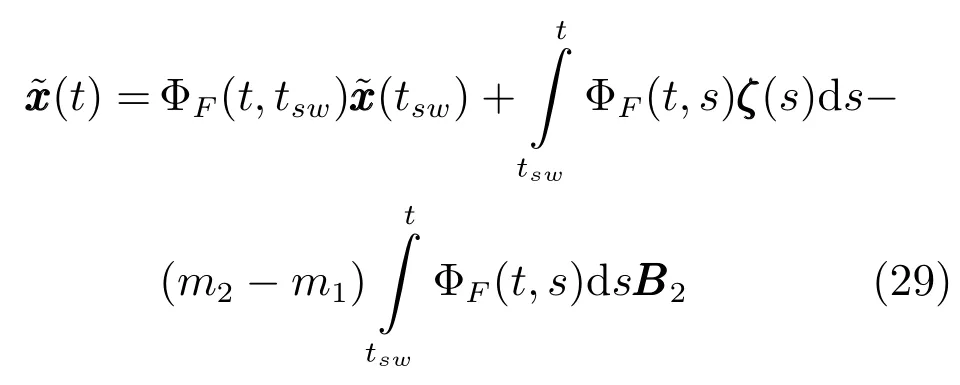

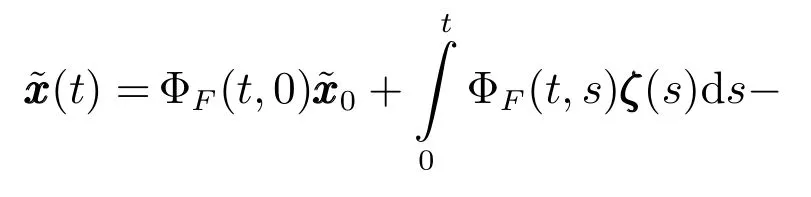
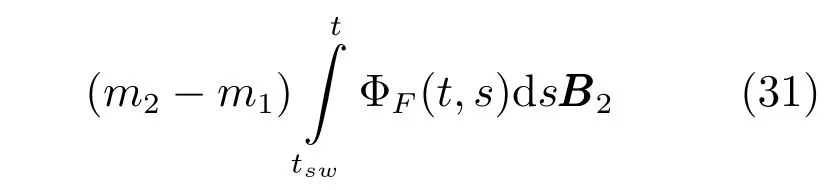




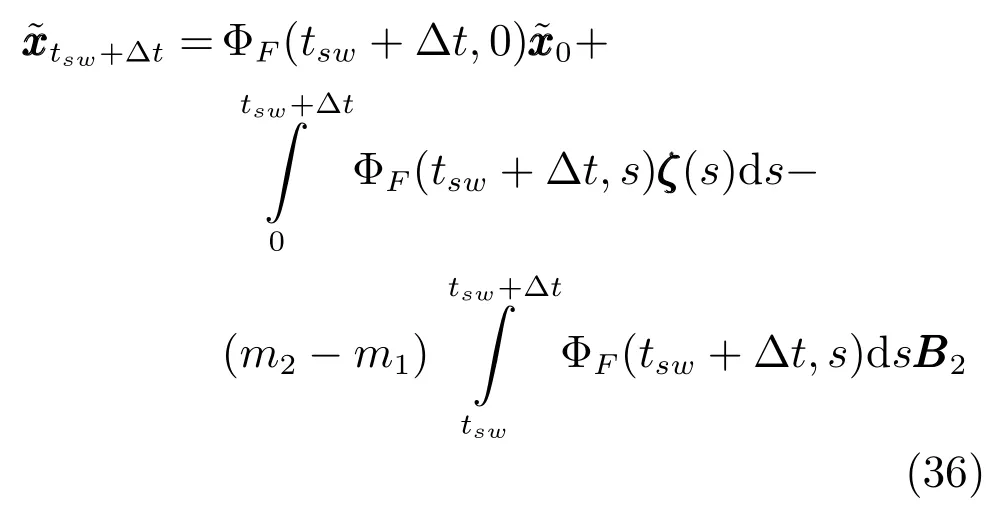
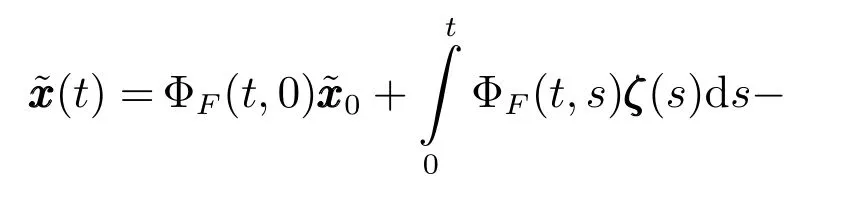
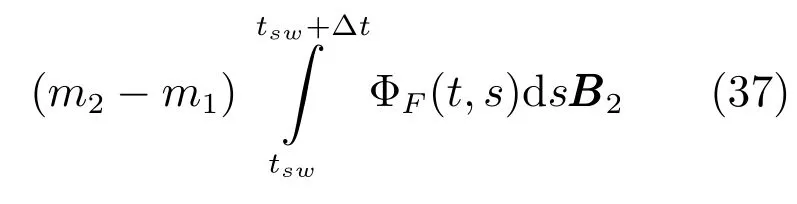


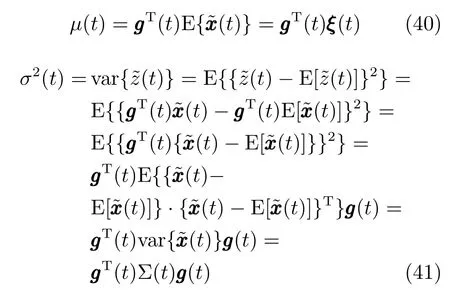
3 仿真实验

4 结论