F-粗糙集视角的概念漂移与属性约简
邓大勇 李亚楠 黄厚宽
现实中的数据往往随着时间推移而变化,例如,证券交易数据、微博、微信、视频、传感器数据等,这种类型的数据称为数据流[1].数据流具有按照时间顺序排列、快速变化、海量甚至无限,并且可能出现概念漂移现象等特征[2−3].概念漂移目前尚无统一定义,是指数据流中概念(或目标变量的统计特性)的不稳定性、不确定性,以及随着时间变化而变化的特征.数据流挖掘是当前数据挖掘研究的一个热点,数据流分类和概念漂移探测是当前数据流挖掘的主要研究方向.
数据流的分类策略主要有:单一分类器[4−6]和集成分类器[3,7−11].概念漂移的探测准则主要有:分类准确率和联合概率.无论是单一分类器还是集成分类器都常用分类准确率(或分类错误率)判断概念漂移,将分类准确率低的分类器进行淘汰或改进,从而提高分类效率.除了分类准确率外,联合概率也常用于探测概念漂移[12−14].分类准确率往往用于通过实验分析探测概念漂移,联合概率则往往用于从理论上对概念漂移进行分析或探测.
粗糙集理论[15−17]是一种处理不精确、不完全、含糊数据的有效数学工具,是数据挖掘和分类的重要方法.属性约简与不确定性分析是粗糙集理论的两个重要应用.传统的粗糙集理论不太适合研究海量的、动态变化的数据,也不太适合研究数据流;F-粗糙集[18−19]是第一个动态粗糙集模型,它将粗糙理论从单个信息表或决策表推广到多个.与F-粗糙集相对应的属性约简方法是并行约简.F-粗糙集和并行约简比较适合研究动态变化的数据,能够研究数据流和概念漂移.
利用粗糙集理论研究数据流和概念漂移比较少见.文献[20−21]利用粗糙集上下近似的变化去度量概念漂移,这种从数据的结构角度度量概念漂移的方法,难以进行移植和扩展,也难以推广应用;文献[22]把每个滑动窗口看成是一个决策子表,利用F-粗糙集和并行约简的方法整体删除冗余属性,通过比较不同子表之间的属性重要性变化探测概念漂移,不受上下近似结构的限制,具有很好的移植性和扩展性.除了并行约简之外,粗糙集理论中还有很多种类的约简,例如,Pawlak约简、互信息约简[23]、条件熵约简[24−25]等.粗糙集属性约简准则往往是不确定性分析的有力工具,例如,对应Pawlak约简、互信息约简、条件熵约简等的属性依赖度、互信息、条件熵等,都是粗糙集理论分析数据不确定性的有力工具.但是,能否直接用粗糙集属性约简准则探测概念漂移?属性约简与概念漂移有什么关系?受文献[22]启发,本文努力揭示粗糙集理论的属性约简和概念漂移之间的内在联系.
本文首先从概念漂移的角度讨论了粗糙集的属性约简与概念漂移之间的联系和区别;其次,探讨粗糙集属性约简观点下的概念漂移准则与传统的概念漂移准则(包括分类准确率和联合概率)之间的区别与联系.在此基础上,提出了属性依赖度和条件熵的概念漂移探测准则,分析了条件熵和联合概率在探测概念漂移方面的联系.理论分析和实验结果显示,与分类准确率一样,属性依赖度和条件熵能有效地探测概念漂移.属性依赖度和条件熵具有联合概率进行理论分析的优点,又具有分类准确率进行实验分析比较的优点,并且可以增加可重用性、减少工作量.
1 基础知识
本节简单介绍粗糙集[15−17]、F-粗糙集和并行约简[18−19]的基本知识.
1.1 粗糙集
IS=(U,A)是一个信息系统,其中U是论域,A是论域U上的条件属性集.对于每个属性a∈A都对应一个函数a:U→Va,Va称为属性a的值域,U中每个元素称为个体、对象或行.
对于每一个属性子集B⊆A和任何个体x∈U都对应一个如下的信息函数:

B-不分明关系(或称为不可区分关系)定义为

任何满足关系IND(B)的两个元素x,y都不能由属性子集B区分,[x]B表示由x引导的IND(B)等价类.
对于信息系统IS=(U,A)、属性子集B⊆A和概念X⊆U,有
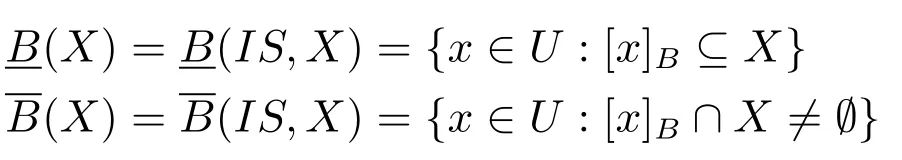
分别称为B-下近似和B-上近似.B-下近似也称为正区域,记为POSB(X).序偶称为粗糙集.
在决策系统DS=(U,A,d)中,决策属性d将论域U划分为块,U/{d}={Y1,Y2,···,YM},其中Yi(i=1,2,···,M) 是等价类. 决策系统DS=(U,A,d)的正区域定义为POSA(d)
有时决策系统DS=(U,A,d)的正区域POSA(d)也记为POSA(DS,d)或POS(DS,A,d).
定义1[15−17].在决策系统DS=(U,A,d)中,称决策属性d以程度h(0≤h≤1)依赖条件属性集A,其中,

符号|·|表示集合的势.
1.2 F-粗糙集
F-粗糙集[18−19]和其他任何粗糙集模型不同,它是关于信息系统簇或决策系统簇的粗糙集模型,这个粗糙集模型比较适合并行计算,也适合研究事物的动态变化.
下面用FIS={ISi}(i=1,2,···,n) 表示与决策系统簇F={DTi}相对应的信息系统簇,其中ISi=(Ui,A),DTi=(Ui,A,d).
定义2[18−19].假设X是一个在不同情形下可能发生变化的概念(即X是一个概念变量),N是一种情形,X|N表示在情形N下的概念X.在一个信息系统簇中,.如果不引起混淆,X|N可以缩写为X.
假设X是信息系统簇FIS中的一个概念,那么X关于属性子集B⊆A的上近似、下近似、边界线区域和负区域的定义如下:
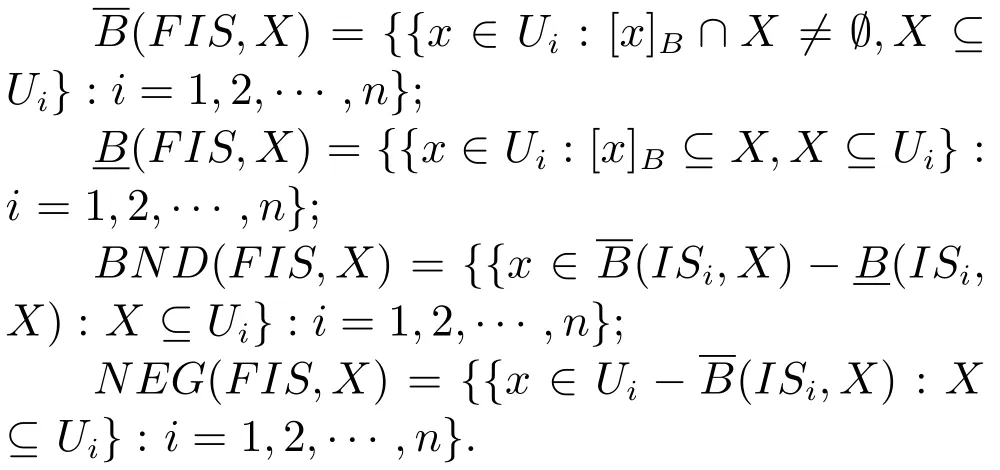
概念X关于信息系统簇FIS的上下近似、边界线区域、负区域分别是FIS中的信息子系统关于概念X的上下近似、边界线区域、负区域组成的集合.序偶称为F-粗糙集.如果则称序偶是精确的.
定义3[18−19].设F是一个决策系统簇,F的正区域定义如下:
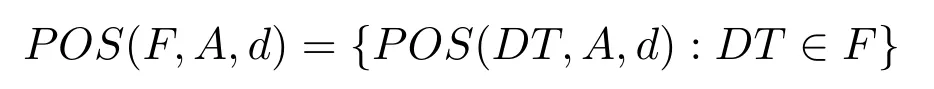
定义4[18−19].设F是一个决策系统簇,称B⊆A为F的并行约简当且仅当满足下面条件:
1)POS(F,B,d)=POS(F,A,d);
2)对任意S⊂B,都有.
2 概念漂移准则分析与比较
概念漂移的评判准则主要分析比较以下三种:
1)分类准确率(或分类错误率).如果分类器对数据集的分类准确率有较大的变化,一般情况下是指分类准确率下降,而且超过了一定的阈值,则称发生了概念漂移.分类准确率是最常用的一种概念漂移探测准则,常常用于实验分析中.
使用分类准确率的变化判断是否发生概念漂移,是一种使用概念漂移的结果进行判断的方法,也是使用最广泛的方法.这种方法依赖实验或实际应用,能够从总体上把握概念漂移,无论是在单一分类器还是集成分类器中都使用最广泛.但是,对于同一训练集得到的分类器,对于同一测试集,如果特征选择不同,则实验结果可能不同.
2)联合概率.联合概率p(X,Y)=p(X)p(Y|X)(其中,X表示由条件属性诱导的概念,Y表示由决策属性诱导的概念)发生变化,而且超过一定的阈值.用联合概率作为概念漂移检测准则又分为虚拟漂移和真实漂移.虚拟漂移[12,14]是指在联合概率中p(Y|X)不发生变化,仅p(X)变化;真实漂移[13−14]是指在联合概率中p(X)不发生变化,而p(Y|X)发生变化.
联合概率的准则也较常用.这种准则因为有较强的数学理论基础(统计理论与概率论),所以,从理论方面研讨概念漂移,人们喜欢使用联合概率的准则.但是,这个准则局限于某些概念,缺乏灵活性,对于整个数据集而言就不太实用.这是因为联合概率p(X,Y)只能针对某些特定的研究其变化,而整个数据集可能是一系列的有序对,它们的概率分布并不相同,也很难用同一个表达式表示,如果用联合概率p(X,Y)研究其变化,难以从总体上把握概念漂移.
3)属性重要性.用属性重要性变化探测概念漂移是文献[22]新提出来的.属性重要性是数据的内部属性,是概念的内涵.用属性重要性准则探测概念漂移,分析属性重要性随着数据的变化而变化,不直接依赖于概念的外延,而且用并行约简进行特征选择,统一了比较准则,避免了特征选择不同对概念漂移探测产生的负面影响,所以,用属性重要性准则探测概念漂移,既有确定性,又有灵活性;既能用于实验检测,又能用于理论分析,兼具有分类准确率准则和联合概率准则的优点.
文献[22]定义的基于属性重要性的概念漂移准则,探测了并行约简后各个属性重要性的变化而引起的概念漂移,但是文献[22]中单个属性重要性的变化不能全面反映数据流中的概念漂移.为了更好地与分类准确率、联合概率分布进行比较,本文定义和使用属性依赖度和条件熵作为概念漂移探测准则.
3 属性约简与概念漂移的对比与分析
粗糙集中有很多种类的属性约简,其中最常用的是基于正区域的属性约简和基于互信息的属性约简.这些属性约简的准则,从概念漂移的角度看,就是在同一数据集中保持在属性约简准则下不发生概念漂移的最小属性子集.但是各种准则并不一定兼容,有时一个准则可能违背另一个准则,也就是说,在一个准则下不发生概念漂移的约简,在另一个准则下可能发生概念漂移.实际上,基于互信息的属性约简等价于基于条件熵的属性约简,但是因为条件熵比互信息更接近联合概率,所以,本文以基于正区域的属性约简和基于条件熵的属性约简为例进行阐述.
定义5[15−17].给定一个决策系统DS=(U,A,d),B⊆A称作决策系统DS的一个约简当且仅当B满足如下两个条件:
1)POS(DS,B,d)=POS(DS,A,d);
2)对任意S⊂B,都有POS(DS,S,d)(DS,A,d).
定义6[15−17].给定一个决策系统DS=(U,A,d),B⊆A称作决策系统DS的一个约简,当且仅当B满足如下两个条件:
1)γ(DS,B,d)=γ(DS,A,d);
2)对任意的S⊂B,均有γ(DS,S,d)(DS,A,d).
定义5从正区域的结构出发定义了属性约简,定义6从属性依赖度角度定义了属性约简;定义5适合理解,定义6适合计算.从概念漂移角度看,定义5的条件属性约简保证决策系统正区域不发生改变,保证正区域部分的条件概率p(Y|X)=1,即正区域部分不发生真实概念漂移;定义6的条件属性约简保证了决策系统的属性依赖度不发生概念漂移;定义5只适合于单个决策表本身,不适合推广.定义6可以从决策子表簇角度进行推广,适合于探测决策子表簇中概念漂移.所以,在决策子表簇中可以将基于属性依赖性的概念漂移准则定义如下:
定义7.在决策子表簇F中,DTi,DTj∈F相对于属性依赖度的概念漂移定义为

定义8[24−25].给定一个决策系统DS=(U A,d),设A和{d}在论域U上导出的划分分别为X和Y,其中,的信息熵分别定义为

{d}相对于A的条件熵定义为

定义9[24−25].给定一个决策系统DS=(U,A,d),若B⊆A满足下列两个条件:
1)H(DS,{d}|A)=H(DS,{d}|B);
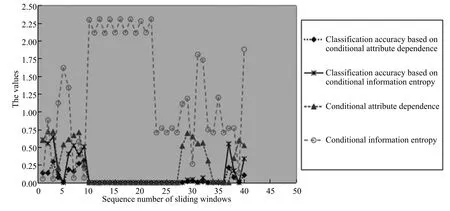
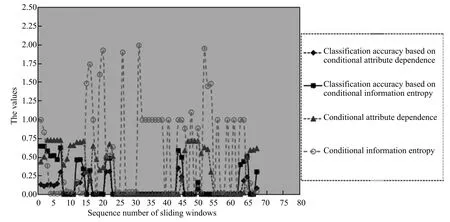
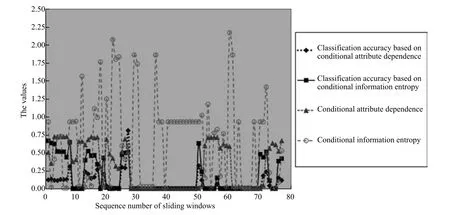
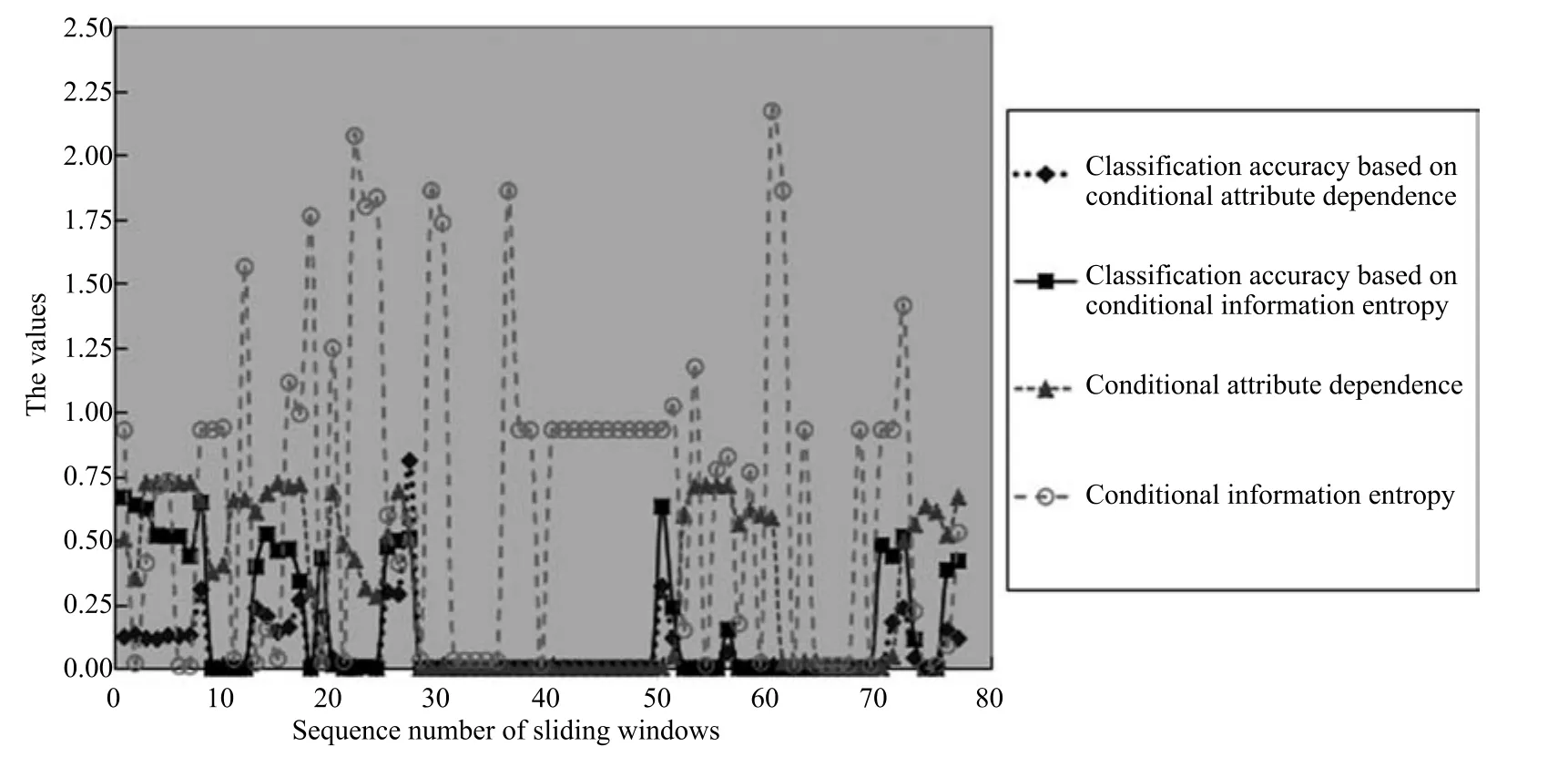
2)对任意b∈B,都有H(DS,{d}|B) 则称B是A的一个基于条件熵的相对约简. 定理1.给定一个决策系统DS=(U,A,d),B1⊂B2⊆A,由B1,B2导出的划分分别为U/B1={X1,X2,···,XN},U/B2={X1',X2',···,XM'},则联合概率有如下关系:p(Xl',Yj)≤p(Xk,Yj),其中Xl'=[x]B2∈U/B2,Xk=[x]B1∈U/B1,Yj∈U/{d}. 证明.对于中的每一块,要么等于中的某一块,要么是某几块的并.不失一般性,有,所以有,即 关于在一个系统中的条件熵随条件属性的变化,有下面引理: 引理1[25].给定一个决策系统DS=(U,A,d),B1⊂B2⊆A,则有 成立. 定理1和引理1说明,在一个决策系统中,联合概率与条件熵都是随着条件属性的增加而单调不增.根据文献[26]的属性约简准则,条件熵可以作为属性约简的准则,联合概率也可以作为属性约简的准则;类似地,联合概率可以作为概念漂移的准则,条件熵也可以作为概念漂移的准则. 定义10.在决策子表簇F中,DTi,DTj∈F相对于条件熵的概念漂移定义为 定理2.在决策子表簇F中,B⊆A是F相对于条件熵的并行约简,DTi,DTj∈F,则约简后相对于条件熵的概念漂移等于约简前的概念漂移,即 定理3.在决策子表簇F中,B⊆A是F相对于属性依赖度的并行约简,DTi,DTj∈F,则约简后相对于属性依赖度的概念漂移等于约简前的概念漂移,即 定理2和定理3根据相关定义可以非常容易证明.定理2和定理3说明,在条件熵和属性依赖度等属性约简的条件下,并行约简不会影响概念漂移的度量和探测,并且并行约简可以将冗余属性删除,减少计算量,彰显对概念漂移发生起作用的条件属性. 通过以上分析和论述,粗糙集和F-粗糙集的属性约简准则可以推广用于概念漂移的度量和探测.概念漂移和属性约简存在一定的内在联系,属性约简是保证单个决策表或决策表簇内部不发生概念漂移的最小属性子集,而一般情况下的概念漂移则是不同的数据集或变化的数据集之间某种度量发生变化而产生的. 定义11.在决策子表簇F中,,其中,并设内涵相同(即它们对应的属性值相等),则的条件熵概念漂移定义为 下面讨论联合概率与条件熵在探测概念漂移方面的关系. 定理4.在决策子表簇F中,,其中,并设X与X'、Y与Y'内涵相同(对应的属性值相等).用联合概率准则探测发生虚拟概念漂移,则用条件熵准则也发生虚拟概念漂移;若用联合概率准则发生真实概念漂移,则用条件熵准则也同样发生真实概念漂移. 证明.反设用联合概率准则没有发生概念漂移,即, 1)在p(X)不变,即的情况下: 2)在p(Y|X)不变,即的情况下. 定理4说明,用联合概率分布能探测到的虚拟概念漂移和真实概念漂移都能用条件熵探测.从上述推理过程可知,定理4的逆定理也成立. 例1.设F={DT1,DT2},如表1和表2所示.a,b,c是条件属性,d是决策属性. 表1 决策子系统DT1Table 1 A decision subsystemDT1 表2 决策子系统DT2Table 2 A decision subsystemDT2 显然,F的并行约简为 于是, 从例1可以看出,无论是从属性依赖度还是从条件熵的角度,只要选取的参数δ<1/3,两种标准都发生了概念漂移. 由此可见,概念漂移和属性约简具有内在的联系.概念漂移探测的有些准则(例如联合概率)能够用于属性约简,反过来,属性约简的准则(例如属性依赖度和条件熵)也能用于概念漂移探测.属性约简就是保证某种准则下不发生概念漂移的删除冗余属性过程.然而,作为不确定性度量指标的属性依赖度仅考虑正区域部分的数据,不考虑非正区域部分的数据,无论是在属性约简方面还是在探测概念漂移方面都忽略了非正区域数据的变化;而条件熵则把所有的数据都考虑在内,在属性约简和概念漂移探测上全盘考虑了数据的变化.所以,我们推测,大部分条件属性约简准则能够用于概念漂移探测,能够用于数据流概念漂移探测的属性约简准则应该满足不依赖于数据的结构,但不同的不确定性指标在属性约简和概念漂移探测方面各具特色.深入分析其他的属性约简准则是否能够用于概念漂移探测,以及研究它们在概念漂移探测方面的区别与联系,是我们下一步研究的内容. 下一节将通过实验比较属性依赖度、条件熵和两种特征选择(属性约简)后的分类准确率作为概念漂移探测准则.这两种特征选择分别是基于属性依赖度的属性约简和基于条件熵的属性约简. 实验数据为KDD-CUP991http://kdd.ics.uci.edu/databases/kddcup99/kddcup99.html网络入侵检测数据10%的子集.该数据包含494021条记录,42个属性.实验中滑动窗口的大小分别为5000和10000,相邻窗口之间有或无10%的重复率,实验中将第一个数据集(滑动窗口)当成训练集,其余的数据集都是测试集. 理论分析和实验结果显示,分类准确率和属性依赖度都属于[0,1],而条件熵的值可以大于1,实验结果也证实了这一点. 图1~4虽然只是显示了这几种准则相对于训练集的值,没有直接显示概念漂移,但只要这些指标数值和训练集相应的指标数值相减,然后取绝对值,并与阈值(可以根据需要自己设定)进行比较,就可以很容易判定是否发生概念漂移.而且图1∼4非常明显地显示,特征选择不同,对同一个数据集的分类准确率不同. 图1~4显示基于属性重要度/条件熵的分类准确率和属性依赖度的整体变化趋势不如条件熵明显,所以条件熵能更加准确地探测概念漂移. 图1显示在第10~27个滑动窗口,基于属性重要度/条件熵的分类准确率的值为0,属性依赖度的值接近于0,变化趋势不明显,均不利于探测概念漂移;在第10~22个滑动窗口,条件熵的变化也不明显,但在探测概念漂移过程中,条件熵优于分类准确率和属性依赖度. 图2显示在第25~43个滑动窗口,基于属性重要度/条件熵的分类准确率的值为0,属性依赖度的值接近于0,变化趋势很不明显,不利于探测概念漂移;虽然在第32~38个滑动窗口,条件熵的变化趋势很小,但是在探测概念漂移的过程中,条件熵优于上述三种方法. 图3显示在第30~50个滑动窗口,基于属性重要度/条件熵的分类准确率的值为0;在第35~65个滑动窗口,属性依赖度的值趋近于0,且变化趋势不大;在第40~50个滑动窗口,条件熵的变化趋势也不明显.但是,条件熵变化不明显的滑动窗口数目较少,因此,条件熵作为概念漂移的探测准则较优. 图4显示在第15~33个滑动窗口,基于属性重要度/条件熵的分类准确率的值为0,属性依赖度的变化较小,均不利于探测是否发生了概念漂移;条件熵的变化能有效的探测概念漂移. 图1 滑动窗口的大小为10000,且相邻窗口之间没有重复Fig.1 The size of sliding windows is 10000 without repeat 图2 滑动窗口的大小为5000,且相邻窗口之间没有重复Fig.2 The size of sliding windows is 5000 without repeat 图3 滑动窗口的大小为5000,且相邻窗口之间有10%的重复Fig.3 The size of sliding windows is 5000 with 10%repeat 图4 滑动窗口的大小为10000,且相临窗口之间有10%的重复Fig.4 The size of sliding windows is 10000 with 10%repeat 从图1~4可以看出,使用这些指标都可以在一定的程度上判定是否发生概念漂移,但分类准确率只能与训练集比较,相邻两个滑动窗口(数据集)之间相对于分类准确率是否发生概念漂移,只能以一个为训练集,另一个为测试集,工作量相当大,而且没有对称性;如果将两个相邻滑动窗口相对于训练集的分类准确率之差进行概念漂移探测,那么很多时候都不利于探测概念漂移.然而使用属性依赖度和条件熵作为概念漂移的判定标准,在元素个数和属性集不发生变化的情况下,每个决策表的属性依赖度和条件熵都是不变的,属性约简也不影响它们的值,任何两个数据集(滑动窗口)之间都可以进行比较,而且具有对称性和可重用性,从而可以减少工作量. 本文从F-粗糙集和概念漂移的角度,揭示了概念漂移和粗糙集属性约简之间的区别与联系.属性约简是在一个信息表内部保持不发生概念漂移的最小属性子集.本文提出了基于属性依赖度和条件熵的概念漂移探测准则,理论分析显示粗糙集的属性约简准则大部分都可用于度量概念漂移,属性依赖度和条件熵具有联合概率分布可进行理论分析的优点,又具有分类准确率可进行实验分析的优点,即将粗糙集的属性约简准则用于概念漂移的探测兼具两种传统的的概念漂移准则的优点.此外,属性依赖度和条件熵作为概念漂移探测准则还具有对称性和可重用性,从而可以减少工作量.所以,F-粗糙集是研究数据流分类和概念漂移,进行数据流分析的非常好的理论和实践工具.将F-粗糙集和粗糙集属性约简准则用于数据流挖掘及概念漂移探测,丰富了数据流挖掘和概念漂移探测的工具,同时,对粗糙集及粒计算理论的发展与应用将起促进作用. 下一步研究重点是将F-粗糙集进一步运用于概念漂移探测和数据流分类,特别是集成分类器的分类研究,并深入研究这些概念漂移准则之间的关系.
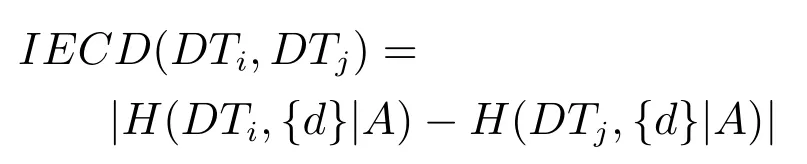


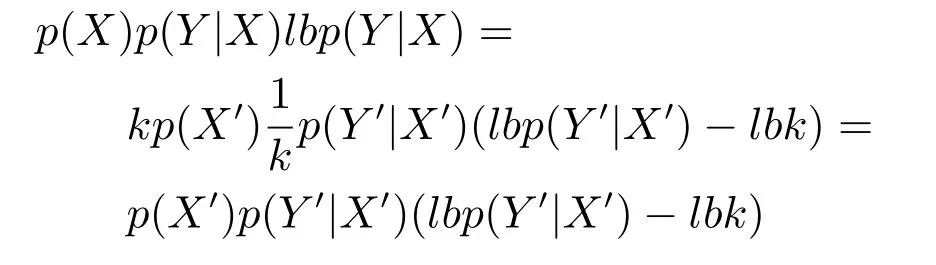
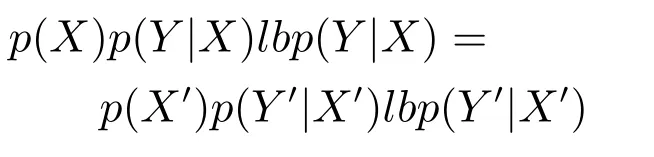






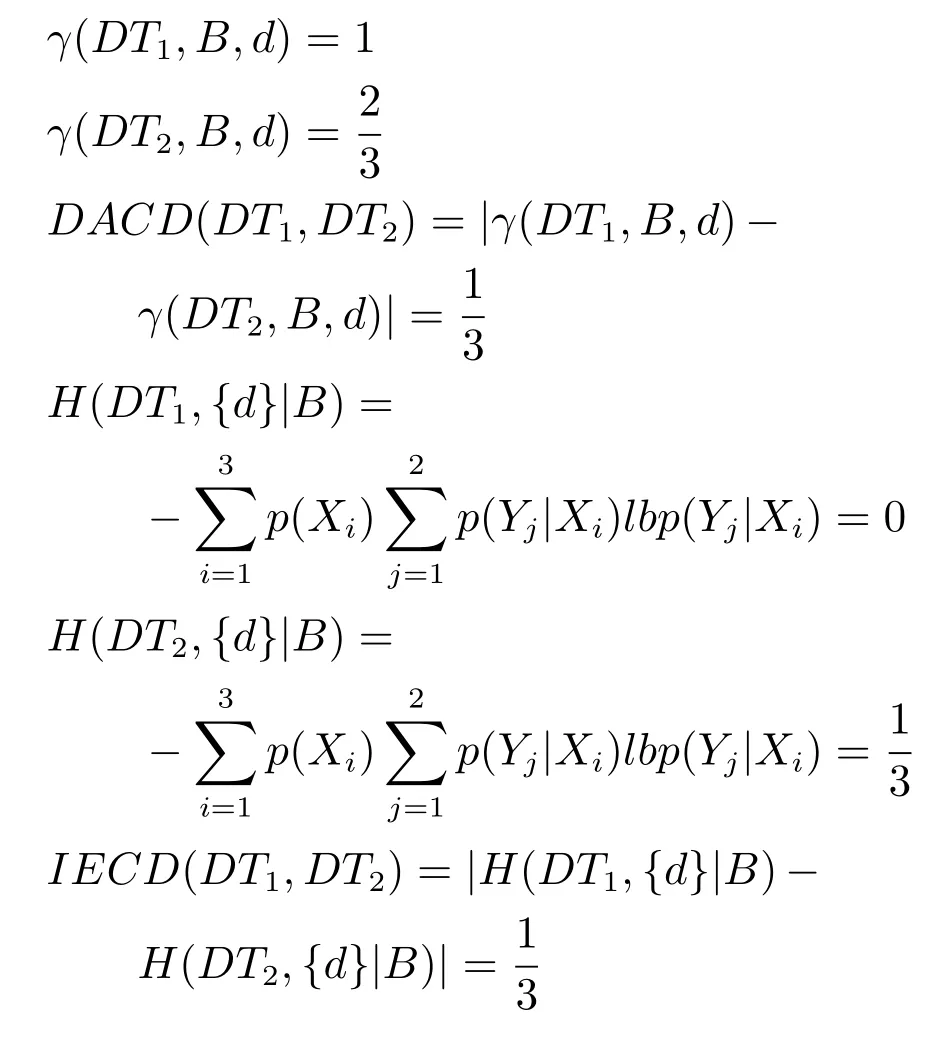
4 实验结果与分析
5 结论与展望

