基于路面一致激励车桥耦合非平稳随机振动分析*
桂水荣, 陈水生, 万 水
(1.华东交通大学土木建筑学院 南昌,330013) (2.东南大学交通学院 南京,210096)
引 言
路面不平顺是影响车桥耦合振动的主要因素之一,因路面不平顺激励可以看成高斯平稳随机过程,考虑车辆在桥上的变速行驶,路面不平顺激励将引起车桥耦合非平稳随机振动。Chatterjee等[1]根据桥面随机不平顺激励样本,计算桥梁冲击系数的均值和偏差。Li等[2]认为桥面不平顺样本的峰值位置对冲击系数有很大影响。经典Monte-Carlo法计算工作量大,工程实践中,人们不但关心响应标准差,而且重视样本的均值及最大值,仅进行少量样本分析,计算结果可信度降低。目前研究车桥耦合随机振动除Monte-Carlo法外,演变随机过程[3]、概率密度演化分析[4]及虚拟激励法[5]也是常用数值方法。
车辆在桥梁上变速行驶,彭献等[6]认为加速度对梁横向振动影响不可忽略。殷新锋等[7]认为车辆制动初期对桥梁的冲击系数较制动末期冲击系数大。方志等[8]认为车辆加速度、前后轮输入激励相关性对桥梁及车辆振动均产生影响。目前研究车辆变速引起的车桥耦合振动响应主要以单次性确定响应为主,单次性确定响应难以有效体现非平稳随机响应的统计效应。彭献等[9]运用虚拟激励法研究车辆变速与共振空间频率关系,认为低频对人体和车辆振动起主要作用。韩万水等[10]分析认为路面一致激励和非一致激励输入对桥梁跨中动响应及频谱特性存在差异。上述文献主要研究车辆变速行驶引起的车辆振动响应或路面输入激励时滞效应对车桥耦合振动影响,车辆变速行驶引起的车桥耦合非平稳随机振动响应相对较少。
基于路面不平顺一致激励输入模型,笔者采用虚拟激励法建立车辆变速行驶的三维车桥耦合非平稳随机振动模型,以江西某高速公路梁桥为背景,通过与Monte-Carlo法结果对比验证文中模型的正确性,重点研究车辆行驶的初速度、加速度对桥梁跨中竖向位移、加速度均方根值及频谱特性的影响。
1 车-桥耦合振动模型
1.1 车辆振动方程
目前,行驶在公路桥梁上的载重汽车主要有两轴、三轴自卸汽车及多轴挂车,笔者选取三轴自卸汽车作为研究对象,考虑车体竖向振动、纵向点头、侧翻以及车轮振动,将车辆简化为“弹簧-质量-阻尼”的三维九自由度振动体系,车辆简化模型如图1所示。

图1 整车模型Fig.1 3D vehicle model with nine degrees of freedom
图中车辆各自由度表示如下:ks1,ks2为前轴悬架弹簧刚度;kt1,kt2为前轴车轮刚度;ks3;ks4为中轴悬架弹簧刚度;kt3,kt4为中轴车轮刚度;ks5,ks6为后轴悬架弹簧刚度;kt5,kt6为后轴车轮刚度;cs1,cs2为前轴悬架阻尼系数;ct1,ct2为前轴车轮阻尼系数;cs3,cs4为中轴悬架阻尼系数;ct3,ct4为中轴车轮阻尼系数;cs5,cs6为后轴悬架阻尼系数;ct5,ct6为后轴车轮阻尼系数;m1,m2为前轴悬架系统质量;m3,m4为中轴悬架系统质量;m5,m6为后轴悬架系统质量;mhb为车体质量;Ihp为车体仰俯转动惯量;Ir为车体侧翻转动惯量;θb为仰俯角;φ为侧倾角;zb为车体竖向位移;z1,…,z6为车辆悬架位移坐标;Bf为前轴宽度,Br后轴宽度;a为前轴到车辆质心距离;b为中轴到车辆质心距离;c为后轴到车辆质心距离。
建立九自由度整车模型振动方程为
(1)

1.2 桥梁振动方程
运用有限元方法将桥梁结构进行离散,建立三维空间有限元模型。对桥梁进行离散时,桥梁振动方程可以写成
(2)

使用典型Rayleigh阻尼,利用模态综合叠加技术,式(2)可以改写为
(3)
其中:I,X,Ω分别为对角质量、阻尼及刚度矩阵;Φ为模态向量矩阵。
1.3 车桥耦合振动方程
假设车辆行驶过程中,车轮与桥面保持不脱离,车辆与桥梁通过车轮与桥面接触点处的位移协调和相互作用力的平衡条件相联系。车辆荷载与桥面板的接触关系可以表示成如图2所示,考虑桥面不平顺激励的影响,汽车荷载通过车轮与桥面接触关系如图3所示。

图2 车辆荷载与桥面板单元接触示意图Fig.2 An example to illustrate the interaction between bridge deck and vehicle

图3 车辆与桥面接触示意图Fig.3 Sketch map of a vehicle running on bridge deck
第i个车轮与桥梁之间相互作用力可表示为
(4)
dvb,i=zi-ri-ϖi(i=1,2,…,6)
(5)
其中,dvb, i为第i个车轮相对于桥面的垂直位移;ϖi为i车轮处桥面板初始竖向位移量;ri为i车轮处的桥面不平顺幅值,zi为i车轮的竖向振动位移。
车辆在三维空间桥梁模型上行驶时,时间积分步内,车辆轮胎作用于桥面板的力,需通过插值函数等效到节点。有限元建模时桥面板及铺装层采用shell63单元进行离散,其插值函数N可表示成
N= [NiNjNkNm]
(6)
(7)
其中:ξ=(x-xc)/a,η=(y-yc)/b;ξ0=ξξs;η0=ηηs;a,b为单元长度;xc,yc为单元形心坐标。
车轮作用于板单元荷载向节点等效,第i车轮相对于桥面的位移及速度可以表示成
dvb,i=-NbiΦq-ri+zi
(8)
(9)
其中,Nbi为i车轮插值函数。
考虑路面不平顺激励后,将式(8)和式(9)代入式(4),可得车辆作用于桥梁的惯性力为


(10)
车轮荷载作用于桥梁的荷载矩阵可以写成
(11)
其中:nl为车轮总数。
单个车轮作用于桥梁的荷载写成向量形式
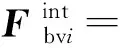
(12)
将式(11)代入式(3)可得
(13)
联立式(12)和式(1),建立车桥耦合振动方程
(14)
其中:Mbv,Cbv,Kbv分别为车桥耦合振动模型的质量、阻尼及刚度矩阵;u为车桥耦合坐标向量,u={q1,q2,…,qr,z1,…,z6,zb,θb,φ}T;Fg为车辆自重引起的动荷载;Fw为路面不平顺激励引起的动荷载。
(15)
2 车桥耦合非平稳随机虚拟激励模型
2.1 六轮路面谱输入模型
设l1和l2为中轮和后轮距前轮距离,B为车辆左右轮的间距,三轴六轮车平面布置如图4所示。

图4 三轴车辆平面布置示意图Fig.4 Plan sketch of a vehicle with three triaxial
路面空间功率谱密度为静态时,其垂直激励可近似看作一种平稳随机过程,因车辆行驶过程中,车速不断变化,输入路面激励实际上是动态非平稳的随机过程。路面不平度系数、左右轮间距、左右轮相干函数,都将影响着各车轮输出的路面不平顺激励响应。六轮相关路面激励功率谱密度矩阵可以表示为
Gq(n) =

(16)
其中:coh(n)=e2πnB为左右轮路面谱激励输入相干函数;Gq(n)为路面不平度系数;n为空间频率。
2.2 车辆匀加速行驶路面谱激励
当车辆以速度v作匀速行驶时,车速与频率时空关系有ω=Ωv,即f=nv。其中,f和n分别表示时间频率和空间频率,v为车速。当车辆以匀加速a行驶时,由t时刻车速vt=v0+at与时间频率和空间频率关系,可得t时刻时间频率函数f=n(v0+at)。其中,v0为初始速度。

(17)
时间频域内的功率谱密度函数可转化成圆频率域内的功率谱密度函数为
(18)
2.3 路面一致激励车桥耦合虚拟激励模型
若不考虑左右车轮轨迹的相干性及各车轴之间路面谱激励输入的时间滞后效应,即输入各车轮的路面谱激励完全不相干,则相干系数coh(n)=0,时滞效应系数为0,相干系数矩阵ρ=diag{1,1,1,1,1,1}。ρ为单位对角矩阵,可以表示成ρ=IIT,I为单位矩阵。设S为各车轮路面输入谱激励幅值矩阵,路面激励的输入矩阵可以表示成
Gq(ω)=SIITS=P*PT
(19)

由式(16)和式(19)构造路面不平顺激励的虚拟激励荷载

(20)
其中:Ie为单位列向量;Tb0,Tb1,Tv0,Tv1为车桥耦合虚拟激励荷载系数矩阵。
将式(20)代入式(14),由路面虚拟荷载激励引起的确定性运动方程可以写成:
(21)
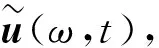
(22)
其中:u*为u的复共轭。
响应方差可通过功率谱密度函数积分求得
(23)
式(23)为无穷限的广义积分,可借助数值积分方法进行求解。实际数值积分计算中的上限一般取有限值,假设取积分区间为[0,ωb],若采用等间距梯形积分公式,式(23)可以写为
其中:m为离散频点数;Δω=ωb/m;ωk=kΔω(k=0,1,2,…,m)。
3 算例分析
3.1 车辆及桥梁动力特性参数
3.1.1 车辆参数
为研究虚拟激励法求解整车模型在路面随机激励作用下车桥耦合振动响应的准确性,选取一辆三轴载重汽车单向行驶,分析装配式简支梁桥竖向振动响应。车辆模型各参数如表1所示。桥面不平顺激励选用GB7031-2005[11]建议的B级路面不平度功率谱(B级路面不平度系数Gq(n0)为64 mm2·m)。

表1 车辆模型参数
3.1.2 桥梁结构参数及动力特性
以某预应力混凝土简支T梁桥为研究对象,主梁跨径30 m,上部结构横向由6片T梁组成,T梁高2 m,单片梁宽2.10 m,桥面铺装为10 cm厚C50混凝土桥面铺装层+10 cm改性沥青混凝土。采用ANSYS软件建立桥梁三维空间有限元模型,运用板单元模拟桥面铺装层,板-壳实体单元模拟主梁。桥面铺装层及横隔板采用shell63板单元,主梁结构采用solsh190板-壳实体单元,有限元模型如图5所示。对结构进行模态分析,提取简支梁桥前10阶自振频率和振型,简支梁桥前十阶自振频率及振型特征如表2所示。

图5 简支梁桥有限元模型Fig.5 The FEM of simple supported beam bridge

模态阶数1234频率/Hz4.1755.37211.3914.28振型特性竖弯(正)竖弯(正)+横向扭转竖弯(反)+横向扭转竖弯(反)模态阶数5678频率/Hz17.2819.4322.3925.60振型特性竖弯(反)+横向扭转横向弯曲+微弱竖弯(反)竖弯(正)微弱竖弯(正)+桥面板局部扭转模态阶数910频率/Hz30.5133.01振型特性竖弯(反)+桥面板局部扭转竖弯(正)+桥面板局部扭转
从表2可以看出,简支梁桥前5阶频率均以竖弯为主,第2阶频率伴随竖向弯曲振型,主梁出现了横向扭转振型;从第6阶振型开始出现横向弯曲,进入第8阶频率后,桥面板开始出现局部扭转振动,随自振频率增大,桥面板局部扭转振动愈明显。
3.2 车桥耦合随机响应校验
3.2.1 车辆加载
为验证笔者提出的整车非平稳随机振动模型及算法正确性,运用虚拟激励法(pesudo-excitation method, 简称PEM)和Monte-Carlo法(运用三角级数叠加法模拟路面不平顺样本,计算单次确定性响应,然后进行统计分析),采用精细积分算法(precise intergration method, 简称PIM)数值迭代格式求解,对比分析单车荷载在简支梁桥上匀速行驶时,各片梁跨中及四分之一位置(L/4)的竖向动位移、加速度时程响应及功率谱密度曲线。根据车辆在桥梁上行驶特性及《桥规》[12],研究车辆按偏载和正常行车道两种工况行驶,PL1(偏载工况):车辆距路缘石0.5 m;BL1(标准行车道工况):车辆按左侧标准行车道行驶。主梁横断面及车辆加载示意图如图6所示。经分析,车辆按PL1工况行驶,边梁及次边梁所承受荷载最大,为车辆行驶最不利工况。文中仅分析车辆按PL1工况行驶的响应。
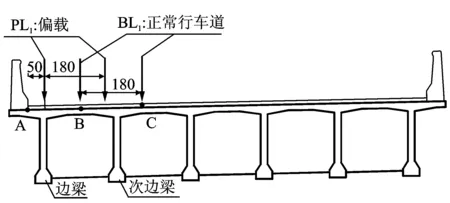
图6 主梁横断面及加载示意图(单位:cm)Fig.6 Sketch map of girder cross section and loading (unit:cm)
3.2.2 车桥耦合随机响应校验
图7 为车辆以25 m/s匀速按PL1工况行驶在B级路面上,Monte-Carlo法及PEM法计算边梁跨中及L/4位置因路面不平顺激励引起的竖向位移均方根响应曲线。Monte-Carlo法统计次数较少时,位移均方根曲线围绕着PEM计算结果上下波动,随着统计次数增加,跨中及L/4位置竖向位移均方根曲线趋近于PEM计算结果。笔者提出的基于PEM整车车桥耦合随机模型准确可行。

图7 Monte-Carlo法与PEM法结果对比Fig.7 Comparison of PEM and Monte-Carlo results for the root mean square curves of the different bridge point
图8给出了车辆按PL1工况以25 m/s匀速通过简支梁桥,路面不平顺激励时滞效应对边梁跨中位置竖向位移均方根的影响。从图8可知,PEM法不考虑路面激励输入的时间滞后效应,Monte-Carlo法与PEM法计算结果接近;PEM法考虑路面输入激励的时滞效应后,跨中竖向位移均方根响应曲线与未考虑时滞效应的Monte-Carlo法及PEM法计算结果存在一定的偏差;车辆未进入跨中之前,时滞效应的跨中位移均方根最大值比未考虑时滞效应大,车桥耦合进行空间分析,需考虑车辆前后各车轮输入路面激励的时滞效应。

图8 时滞效应对跨中位移均方根影响Fig.8 The displacement RMS curve concerning time-lag effect at mid-span
3.3 变速非平稳随机响应分析
图9和图10为车辆以10 m/s 的初速度、不同加速度通过简支梁桥B级路面,边梁跨中竖向位移、加速度均方根响应及加速度功率谱密度曲线图。车辆行驶加速度为零时,即车辆匀速通过简支梁桥,跨中位移及加速度均方根响应曲线峰值均最小。车辆行驶加速度为6 m/s2,跨中最大位移均方根为0.411 6 mm,匀速行驶时的跨中最大位移均方根为0.141 5 mm,随着加速度增加,位移峰值逐渐增大,且出现最大响应时车辆加载位置接近。与位移响应变化规律不同,加速度响应峰值并不随车辆行驶加速度单调增大。车辆加速度为4 m/s2时,跨中加速度均方根响应最大值均较加速度为2,6 m/s2均小,出现加速度峰值的车辆加载位置并不相同。同时,从图10可以看出,随着车辆行驶加速度增大,路面激励与车桥耦合共振的空间频率区间加大,共振功率谱幅值降低。车辆匀速行驶引起的共振频率与匀加速行驶引起的共振频率有偏离;匀速行驶的共振频率区间较小、且峰值较大。车辆匀加速行驶,梁底加速度功率谱在低阶频率未出现共振频率峰值;车辆匀速行驶在桥梁基频4 Hz处出现较小的共振频率峰值。车辆匀加速行驶,梁底在12 Hz与路面空间频率出现共振峰值,匀速行驶则在14 Hz处出现共振峰值;行驶加速度大小直接影响路面激励与车桥耦合共振频率的大小及区间长度。

图9 车辆行驶加速度对跨中动响应的影响Fig.9 The dynamic response of mid-span concerning different vehicle acceleration

图10 车辆行驶加速度对跨中加速度功率谱曲线的影响Fig.10 The acceleration power spectrum of different vehicle acceleration
图11给出了车辆以不同初速度和加速度行驶时,跨中竖向位移和加速度均方根最大值随行车速度变化关系图。相同行驶加速度下,车辆行驶初速度越大,跨中位移和加速度均方根最大值逐渐增大,初速度达到20 m/s时,位移及加速度均方根随车速变化平稳,这主要是因车辆在桥上行驶时间较短,车辆加速行驶效应未能有效体现;桥梁跨中位移及加速度均方根最大值随车辆行驶加速度呈现先快后缓的增长趋势,但并不成线性关系。

图11 车辆变速行驶对跨中动响应最大值的影响Fig.11 The maximum dynamic response of variable vehicle at mid-span
4 结束语
基于路面不平顺一致输入激励,采用虚拟激励法建立车辆变速行驶三维车桥耦合非平稳随机振动模型。以某简支梁桥为例,分析车辆变速通过简支梁桥随机振动响应,结果表明:PEM法与Monte-Carlo法计算结果能较好吻合,表明笔者提出的算法有效;研究空间车桥耦合随机振动响应,路面激励输入的时滞效应不可忽略;车辆行驶最大瞬时速度是决定跨中位移和加速度响应的主要因素;路面激励与车桥耦合的共振频率峰值车辆匀速行驶比匀加速度明显。
——走进广东富华重工制造有限公司

