基于量子遗传支持向量机的流体惯容预测模型*
沈钰杰, 陈 龙, 刘雁玲, 杨晓峰, 张孝良, 汪若尘
(江苏大学汽车与交通工程学院 镇江, 212013)
引 言
传统机械隔振网络以“质量-弹簧-阻尼器”为基础。然而,质量元件在应用中需以地心为参考系,是单端点机械元件,其隔振潜能及推广应用受到限制。针对上述缺陷,Smith[1]最早提出“惯质”概念,并给出具有两个端点的惯容器实现装置,其隔振潜力已在车辆悬架[2-6]、火车悬架[7-8]、建筑物隔振[9]及机械隔振系统[10-11]得到证实。目前常见的惯容器实现形式有滚珠丝杠式、齿轮齿条式[12]、液压-泵式[13]。文献[14]建立了包含滚珠丝杠惯容器背隙、摩擦力及丝杠弹性效应的惯容器非线性模型,讨论了非线性因素对悬架性能的影响。文献[15]对液力式惯容器进行仿真测试,研究了摩擦力及流动压力损失对惯容器力学性能的影响,并开展了试验研究证明了理论模型的正确性。孙晓强等[16]最早提出应用人工智能算法对滚珠丝杠式惯容器进行力学性能预测,取得了较好效果。
Swift等[17]利用流体流经细长管径而产生的惯性效果,设计了一种新型流体式惯容器,然而,由于受摩擦、压力损失及流体非线性因素的影响,无法建立其准确的数学模型。为准确掌握流体惯容器的力学性能,笔者研制了流体惯容器装置并开展了台架试验,在深入分析流体惯容器受非线性因素的影响基础之上,为解决传统神经网络在小样本预测精度不够理想的难题,将量子遗传算法与支持向量机相结合,构建流体惯容器力学性能的智能预测模型,并利用台架测试数据检验所建模型的预测精度。
1 流体惯容器的工作原理
1.1 流体惯容器的结构
理想惯容器的动力学模型可表示为
F=b(a1-a2)
(1)
其中:F为施加在惯容器两端点的一对力;a1,a2为两端点的绝对加速度;b为惯质系数,kg。
流体惯容器主要由机械式液压缸与细长的螺旋管组成,其结构示意图如图1所示。

图1 流体惯容器结构示意图Fig.1 Structure diagram of fluid inerter
图1中,当流体惯容器两端点受到一对力F的作用时,活塞杆连同活塞推动液压缸筒左侧的流体进入细长螺旋管,流经细长螺旋管的过程中,流体的惯性效应为惯容器的实现提供了可能。可以看出,与现有的惯容器实现方式相同,流体惯容器利用细长的螺旋管实现将流体在液压缸内的平动转化为螺旋管中的旋转运动,由此形成“液体飞轮”的作用效果。流体惯容器与现有的滚珠丝杠惯容器、齿轮齿条惯容器相同,均具有两个自由运动的端点,可作为独立的隔振元件融合设计于隔振系统结构中,其提供的惯性作用力可有效阻隔低频段振动的传递,具备有效的减振效果。
1.2 惯质系数的确定
理想状况下,假定液压缸装置密封良好,且油液不可压缩。液压缸内的有效截面积S1为
(2)
其中:r1为活塞杆半径;r2为液压缸内半径。
细长螺旋管的有效截面积S2可表示为
(3)
其中:r3为螺旋管半径。
因此,螺旋管中流体的质量m可表示为
m=ρS2l
(4)
其中:l为螺旋管长度;ρ为流体密度。
当活塞移动位移x时,根据流体体积守恒原则,得到
(5)
其中:h为螺旋管螺距;r4为细长螺旋管的螺旋半径;θ为流体进入螺旋管中相应的转角。
流体在螺旋管中转动产生的转动惯量J为
(6)
根据能量守恒定理,可得
(7)
由此可以确定惯质系数的表达式为
(8)
由式(8)可以看出,流体惯容器的惯质系数取决于螺旋管中的流体质量、螺旋管的螺距、螺旋半径与截面积以及液压缸的有效截面积。因此,可以通过以上设计参数以获取符合工程需要的惯质系数数值。文中研制的流体惯容器结构参数如表1所示。

表1 流体惯容器结构参数
根据式(8)计算得到流体惯容器的惯质系数为370 kg。
2 台架性能测试
2.1 试验方案
文中的流体惯容器力学性能试验在美国INSTRON8800单通道液压激振台上进行,试验中,流体惯容器的上端与激振台固定,下端与自由端激振头固定,具体布置方案如图2所示。

图2 台架测试Fig.2 Bench Test
在力学性能试验[16]中,采用典型的正弦位移型信号作为激励输入,惯容器两端点的力作为响应输出。为避免输入振幅过大导致激振台超负荷,在高频时使用小振幅输入,具体试验方案为0.1~1 Hz的位移输入为20 mm,2~9 Hz的位移输入为10 mm,10~15 Hz的位移输入为5 mm。试验中,通过激振头自带的力传感器信号可实时采集力信号并存储到控制台。
2.2 结果分析
表2给出了流体惯容器的力学性能试验幅值Fe与理论幅值Ft对照结果。

表2 力学性能测试结果
图3~5给出了激振频率为0.1, 5与10 Hz时流体惯容器力学响应的时域图。
根据表2及图3~5可以看出,流体惯容器的力学性能输出呈现出强非线性的特点。在低频段,试验得到的幅值与理论幅值相差较大,这主要是由于流体惯容器在低频段受摩擦力影响显著,此处的摩擦力主要来源于液压缸内壁与活塞之间的滑动摩擦。然而,与机械式滚珠丝杠惯容器不同的是,在低频段输入激振频率为0.1 Hz时,流体惯容的力学输出并非单纯的近似方波[18],而是呈现出正弦型曲线模式,说明此时除了摩擦力外,液压缸内的流体阻尼效应也起着重要作用。若阻尼效应为零,则输出力即为滑动摩擦力,其形状近似方波,而阻尼效应的存在使得原有的滑动摩擦力产生畸变而形成正弦型曲线,当阻尼效应逐渐增大,滑动摩擦力占据的比重越来越小,流体惯容器的输出力均为正弦型曲线。
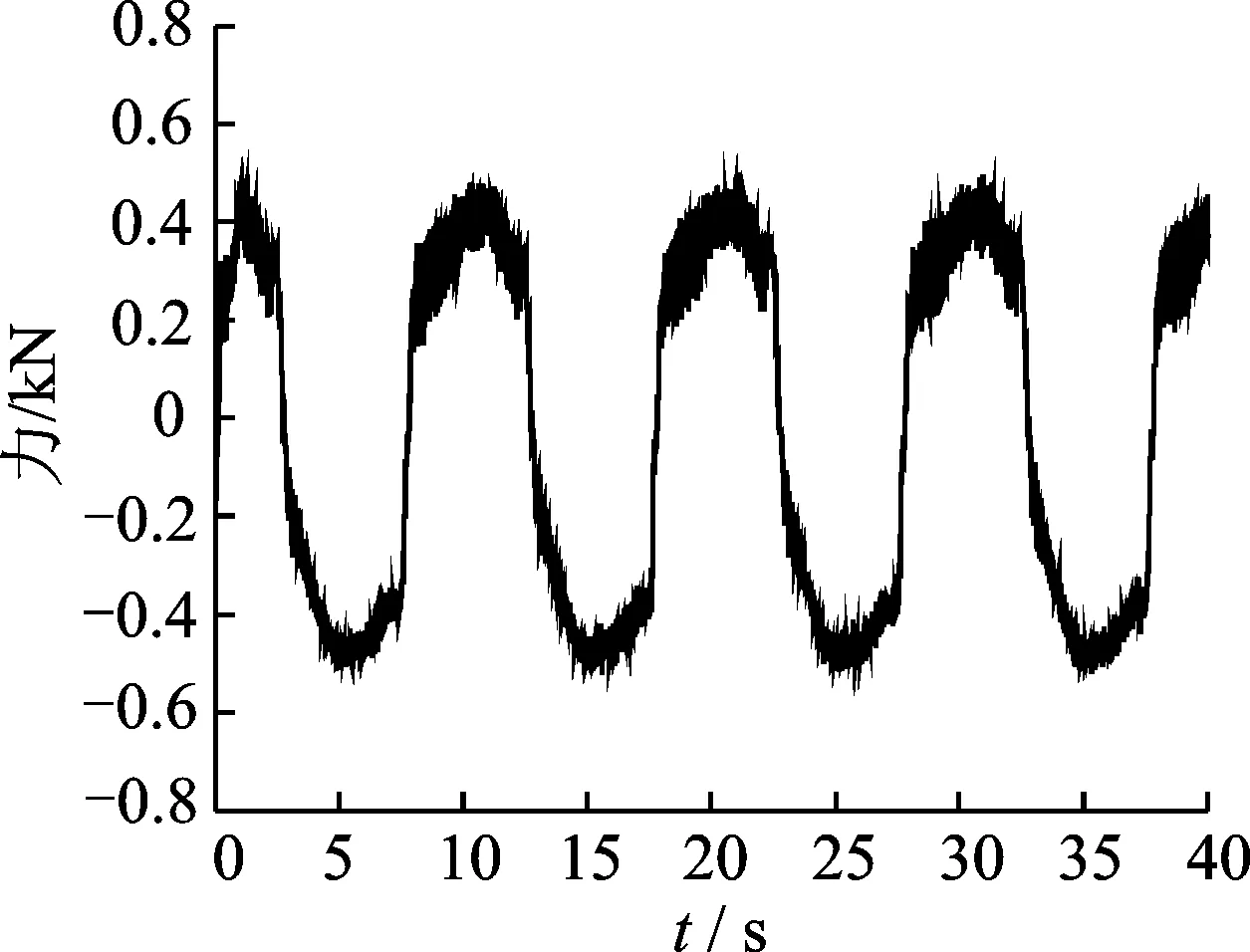
图3 0.1 Hz力学响应
Fig.3 Force response under 0.1 Hz
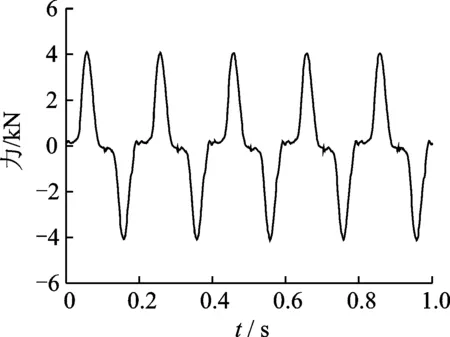
图4 5 Hz力学响应
Fig.4 Force response under 5 Hz
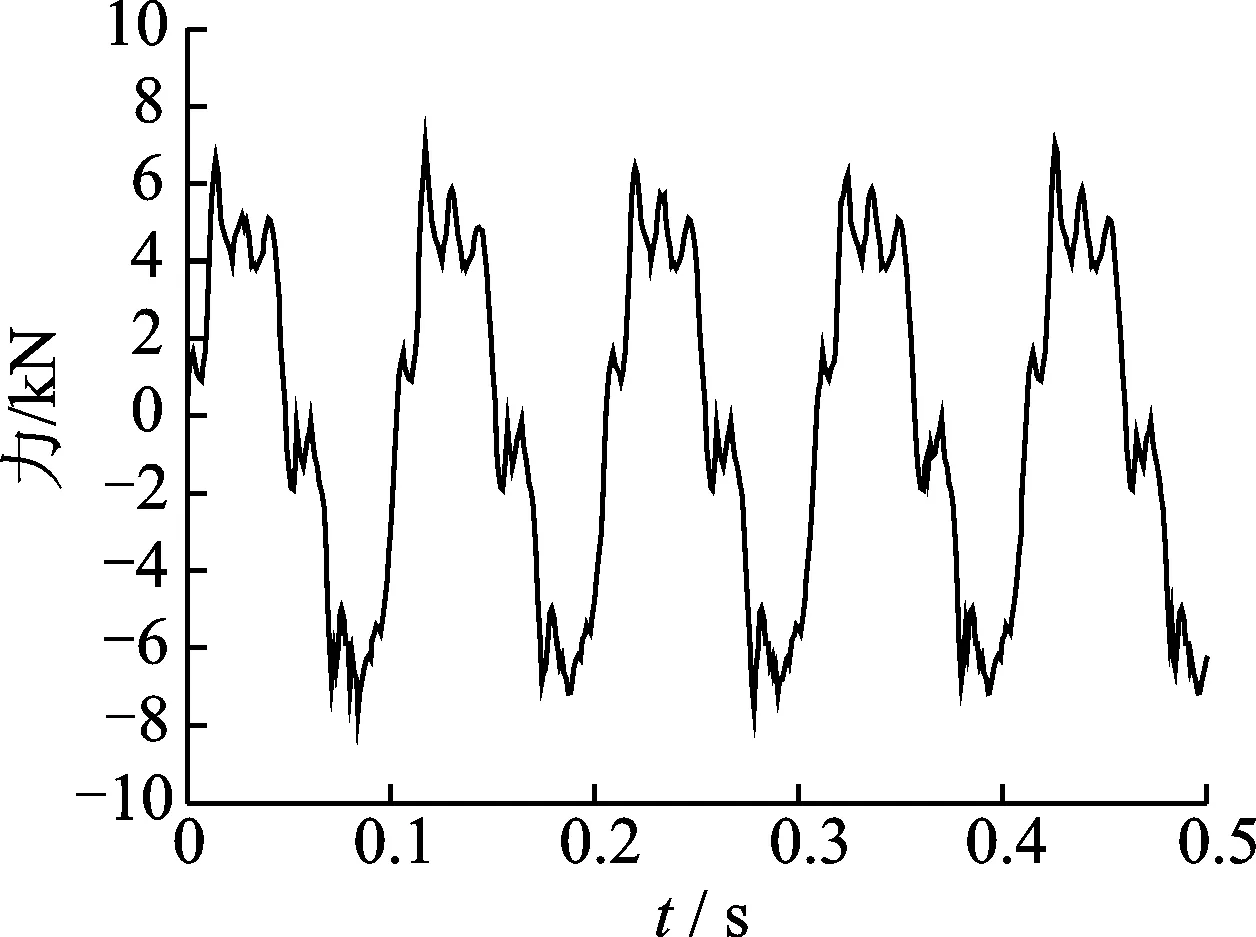
图5 10 Hz力学响应
Fig.5 Force response under 10 Hz
随着激振频率的增加,试验得到的力学输出幅值与理论幅值较为接近,但通过图4及图5可以看出,流体惯容器的力学输出在周期性正弦曲线的基础上出现了许多非线性影响因素,包括油液的泄露、间隙及弹性效应等,主要集中在平衡位置(速度最大)与位移极限位置(振幅最大)处,其力学响应曲线均出现一定程度的波动。在平衡位置处,由于此时处于振动的速度最大处,流体的阻尼效应使得产生较大的阻尼力,同时油液的泄露与空隙会导致空程畸变[19-20]的产生。而在极限位置处,由于此时振幅处于最大位置,加速度也处于最大位置处,流体惯容器的换向运动与间隙、弹性效应的影响,造成了力学输出曲线的波动。
通过上述分析可知,流体惯容器的力学性能输出受摩擦力、间隙非线性、弹性效应等综合影响,仅从数学解析的角度无法准确获取流体惯容的力学性能输出,因此,拟运用在分类、模式识别等领域广为运用的支持向量机对流体惯容器的力学性能进行预测。
3 量子遗传支持向量机预测模型
支持向量机(support vector machine,简称SVM)是一种基于统计学习理论的机器学习方法,其突破了数据维数的限制,可实现样本误差与结构风险的双最小化,具有较强的泛化能力,因此被广泛应用在故障诊断[21-22]与预测技术[23-24]上。
首先,建立含有n个训练样本的训练样本集{(xi,yi),i=1,2,…,n},其中:xi(xi∈Rd)为第i个训练样本的输入列向量;yi∈Rd为对应的输出值。
对于非线性系统而言,可以通过选择核函数来代替点积运算,从而减小计算量。常见的核函数有线性、d阶多项式、径向基核函数与Sigmoid核函数。笔者选取泛化能力与模型预测正确率均较优的径向基核函数进行预测模型的构建,其表达式为
(9)
由此可以得到最优分类函数的表达式为
(10)
模型的预测效果可以通过均方误差E与决定系数R2来决断
(11)
(12)

为减小训练误差并提升预测模型的准确性,对采集的样本数据进行归一化处理,并引入惩罚因子C。在模型的构建中,模型参数g(径向基核函数中的方差)与惩罚因子C的选取对模型的预测性能有较大影响,因此考虑利用全局搜索能力较强的量子遗传算法对C与g进行优化求解。
量子遗传算法[25-26](quantum genetic algorithm,简称QGA) 将量子计算与遗传算法进行有效结合,采用量子比特作为信息的储存单元,并运用量子旋转门作为粒子的更新操作,具备比常规遗传算法更好的寻求效果。量子旋转门的调整操作为
(13)

现结合流体惯容器力学性能试验工况构建基于量子遗传支持向量机的预测模型,但所构建的预测模型方法不局限于所采用的试验工况。在优化过程中,为确保算法的有效性,并能够快速收敛得到优化解,设定遗传算法的种群大小为50,进化代数为100。惩罚因子C越大,所得的支持向量数越多,导致计算量增大,为简化计算,优化变量的取值范围均设置为[0,10],利用训练样本进行训练,以均方误差E作为遗传优化的适应度函数,经过优化求解,得到惩罚因子C的取值为0.4,核函数中的方差g取值为0.6。
在样本的采集输入中,以流体惯容器自由端在时间序列中某时刻的位移输入、速度输入与加速度输入组成的列向量构成输入样本,以惯容器两端点的力信号作为输出向量。由于激励输入为正弦型位移输入,可通过位移型输入表达式推导得到速度输入与加速度输入的曲线表达式。为提高预测精度,每个工况采集100组数据点,在不同频率下对流体惯容器的力学性能进行预测输出。在Matlab环境下读取采集到的样本数据,利用Svmpredict函数进行仿真测试,并对输出的预测值进行对比。
4 结果分析
为便于分析,文中采用在每个工况测试的100组数据点中,随机抽取70组样本数据作为支持向量机训练样本,另外30组数据作为测试数据。图6~8给出了激振频率为0.5, 3, 10 Hz下的流体惯容器预测输出。

图6 0.5 Hz力学预测输出
Fig.6 Predict force under 0.5 Hz

图7 3 Hz力学预测输出
Fig.7 Predict force under 3 Hz
图8 10 Hz力学预测输出
Fig.8 Predict force under 10 Hz
表3给出了3种频率下流体惯容器力学预测输出的均方误差E与决定系数R2。
分析可知,激振频率在0.5 Hz下,采用量子遗传算法优化的QGA-SVM预测模型的决定系数由97.04%提升至99.01%,均方误差由0.004 852降至0.002 373,降幅达51.09%;激振频率在3 Hz下,QGA-SVM预测模型相较于SVM预测模型的决定系数由97.61%提升至99.41%,均方误差由0.002 945降至0.001 138,降幅达61.36%;在激振频率为10 Hz情况下,相较于SVM预测模型,改进的QGA-SVM预测模型的决定系数由97.35%提升至99.32%,均方误差由0.003 779降至0.001 475,降幅达60.97%。综上可以看出,虽然SVM预测模型已具备较好的预测精度,但在工程应用中,能够准确实现目标输出的跟踪具有实际的工程应用价值,采用笔者提出的QGA-SVM预测模型具备更高的预测精度,更适应于工程应用。

表3 预测输出参数
5 结束语
流体惯容器作为一种新型的惯容器实现方式,其力学性能受摩擦力、流体寄生阻尼、装置弹性效应等因素的影响,呈现出复杂的非线性特征,通过力学性能试验可有效揭示非线性因素对流体惯容力学输出的影响机理。利用支持向量机对小样本数据进行训练,笔者构建的流体惯容器预测模型可对流体惯容器的力学性能输出进行准确预测。经由量子遗传算法优化后的支持向量机预测模型具备更高的预测精度,训练集的均方误差最高可下降61.36%。采用智能算法对流体惯容器的力学性能进行预测,可有效掌握惯容器的力学性能输出与输入变量的对应关系,为准确建立惯容器的动力学模型提供新思路。在工程应用中,可有效构建流体惯容器输入与输出之间的对应关系,为工程隔振系统的精确建模提供新方法。

