超深水钻井船波浪载荷计算分析

，，

(中远海运重工有限公司 技术研发中心，辽宁 大连 116600)

由于钻井作业的需要，钻井船在船舯附近会布置垂向贯穿船体，与海水相连通的月池结构，而该处往往是钻井船总纵弯矩最大的位置。同时，月池开口打断了船体纵向构件的连续性，对船体结构强度造成了不利影响[1]。此外，月池角隅点具有较大的应力集中系数，是疲劳评估重点关注的区域。因此，波浪载荷预报的准确度对钻井船结构的可靠性评估非常重要[2-3]。波浪载荷的预报理论和计算手段已经比较成熟。其中三维线性理论是工程中应用最为广泛的方法[4]。

考虑以一艘无限航区的超深水钻井船为研究对象，应用WASIM软件对目标船的波浪弯矩进行直接计算。将波浪弯矩直接计算值与规范计算值进行比较，以论证对于钻井船这类工程型船舶进行波浪载荷直接计算的必要性。

1 钻井船模型概述

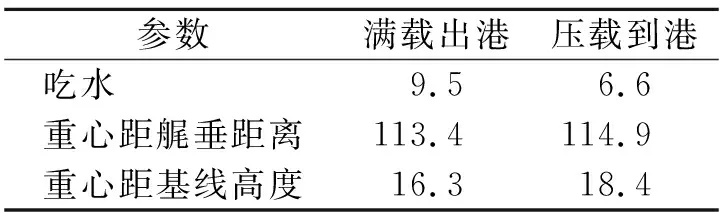
目标钻井船为一艘超深水钻井船，作业水深可达3 658 m，最大钻井深度为15 240 m，可变载荷为35 000 t。其主尺度见表1，月池形状见图1。

钻井船满载与压载计算工况信息见表2。

1.1 船体网格模型

钻井船船体元面网格为正交性很好的四边形网格，半船体湿表面网格数为2 088个，网格精度满足计算要求。见图 2。

表1目标船主尺度m

型长233.0 型宽 43.4 型深 22.4 月池长度 34.3 月池宽度 11.2 设计吃水 9.5

m

波浪载荷计算所需的质量模型以沿船长分布质量点的形式输入，质量模型的重心纵向位置与面元模型的浮心纵向位置相同，质量模型的重量与面元模型的排水量一致，质量模型的横摇、纵摇和首摇惯性半径应与相应的装载工况一致。

钻井船波浪载荷计算的剖面位置分布见表3，全船共有20个剖面。

表3 波浪载荷计算剖面

1.2 计算浪向与周期

浪向和波浪周期参数见表4。浪向定义：从船尾到船首为0度浪向；从右舷到左舷为90度浪向。波浪周期的计算范围应能准确代表计算海域波浪能的分布范围和船体的响应特性。

表4 波浪方向与周期

1.3 月池的影响

进行钻井船波浪载荷计算时，在月池活塞和晃荡共振频率点处，月池内流体的共振运动会导致在月池结构处船体横剖面上波浪载荷RAO出现异常峰值，造成计算结果失真。对于月池的处理，相关文献[4]和船级社推荐作法是，全船湿表面面元模型中不建立月池结构。

1.4 粘性横摇阻尼

粘性横摇阻尼对船体的横摇运动有重要影响，其与船体的舭部形状、舭龙骨尺寸，以及横摇运动速度密切相关。不同回复周期的横摇运动幅值对应的黏性横摇阻尼是不同的，应用随机线性化方法对粘性横摇阻尼进行线性化[6]。

1.5 长期预报

根据挪威船级社规范[7]的要求，无限航区钻井船在航行工况下，波浪弯矩长期预报的海浪条件为北大西洋波浪散布图，海浪谱为PM谱，应用威布尔分布进行长期拟合，海浪谱方向函数为二次余弦函数，其他参数见表5。

1.6 短期预报

根据北大西洋波浪散布图，20年 一遇的海况查阅美国船级社指南[8]，目标海况的有义波高为15.1 m，对应的平均上跨零周期在11～12 s附近。在这样的极端海况下，为了避免钻井船发生过大的横摇运动而导致船体倾覆，在DP-3动力定位系统的帮助下，目标船的艏向角会保持在±30°的范围内。因此，目标船波浪弯矩短期极值计算的浪向角范围为150°～180°。其他海况参数见表6。

表5 长期波浪载荷预报的波浪环境条件

在有义波高为15.1 m的恶劣海况下，船体摇荡运动十分剧烈，而且还会遭受严重的波浪增阻，这些因素都会导致钻井船失速，故计算分析时，只考虑零航速情况。

表6 航行工况海况条件

2 结果与讨论

2.1 短期极值与长期极值

目标船压载状态不同平均上跨零周期海况时，波浪弯矩短期预报极值(即，短期预报最有可能的最大值)沿船长的分布见图3。满载工况下，不同周期短期海况下的波浪弯矩极值则见图 4。由图3、4可知，不论是压载状态还是满载状态，目标船波浪弯矩的最大短期极值都发生在平均上跨零周期为TZ=10.5 s的海况，而且随着周期的增加，船中处波浪弯矩极值逐渐变小。

在平均上跨周期为10.5 s的海况以及3种不同浪向下，钻井船在压载和满载状态波浪弯矩极值分布信息分别见图5、6。如图所示，180°浪向下，波浪弯矩短期极值最大；而且150°浪向下，波浪弯矩短期极值最小。故以平均上跨零周期Tz=10.5 s，180°浪向下的海况作为目标船的设计海况，并以此设计海况下波浪弯矩的短期极值与长期统计极值进行对比分析。

在压载和满载2种状态下，波浪弯矩长期与短期预报极值的对比情况分别见图7、8。选取沿船长分布最大的波浪弯矩计算值作为波浪弯矩的设计值。由此可知，不论是压载状态还是满载状态，波浪弯矩长期设计值与波浪弯矩的短期设计值都出现在距船艉108 m处的剖面上。压载状态，波浪弯矩短期设计值为4.52×109N·m，波浪弯矩长期设计值则为4.27×109N·m，相对误差为5.85%；满载状态下，波浪弯矩短期设计值增加到4.90×109N·m，对应的长期设计值为4.65×109N·m，相对误差为5.4%。相同概率水平下，波浪弯矩的长期设计值小于其短期设计值，但是相对误差不超过6%。

除了波浪弯矩短期设计值大于长期设计值外，还有一个现象值得注意：两种装载状态下，目标船前半部分船体，波浪弯矩的短期极值明显高于长期极值。造成两者之间出现明显差距的原因是两种统计方法对浪向角处理方式的不同：目标船进行波浪载荷长期预报时，计算了0～180°全部浪向下波浪弯矩的传递函数，并且以等概率水平考虑了全部浪向对波浪弯矩的影响；而开展波浪载荷短期预报时，只进行了180°顶浪状态下波浪载荷的计算，没有考虑其他浪向对波浪弯矩计算的影响。在顶浪状态下，船体前半部分的纵摇运动会明显大于其他浪向下的计算结果，进而具有较大的垂向加速度；而且顶浪状态下波浪弯矩也大于其它浪向下的值。所以，同概率水平下波浪弯矩的短期设计值会大于长期设计值，以及目标船前半部分的波浪弯矩短期极值会明显大于长期极值。

2.2 波浪载荷长期计算值及与规范值的比较

参照挪威船级社规范[9]给出的钻井船垂向波浪弯矩的规范计算公式。

中垂波浪弯矩为

Mwo,s=-0.11CwL2B(Cb+0.7)

中拱波浪弯矩为

Mwo,h=0.19CwL2BCb

式中：Cw为波浪系数，对于目标船取值为10.11；L为规范船长，226.017 m；B为型宽；Cb为相应吃水下的方形系数，但是不能小于0.6。

根据挪威船级社规范[10]要求，在极限海况下，由线性理论计算得到的波浪弯矩应该进行非线性修正，修正系数见表7。

表7 波浪弯矩非线性修正系数

考虑非线性修正后，满载状态下波浪弯矩的长期极值与规范值的对比见表8。

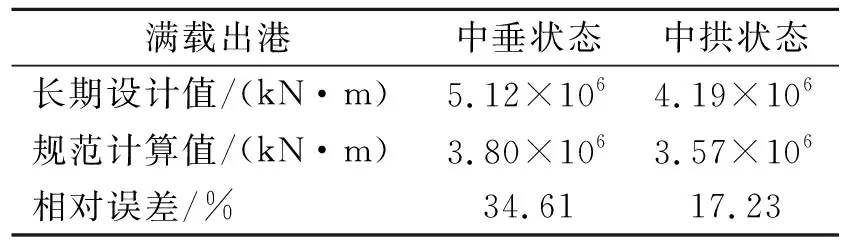
表8 满载出港波浪弯矩直接值与规范值对比

压载到港波浪弯矩直接值与规范值对比见表9。如表9所示，压载状态波浪弯矩的长期计算值与规范计算值的对比关系与满载时的情况相同，即波浪弯矩长期预报极值大于规范值。

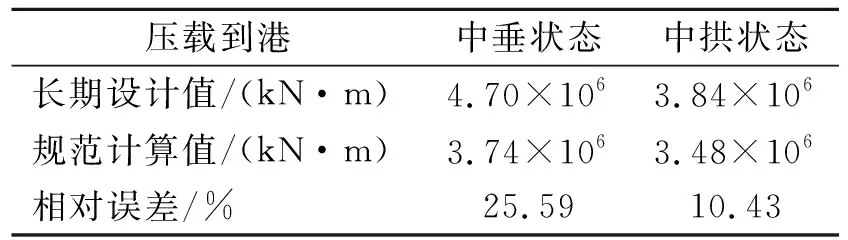
表9 压载到港波浪弯矩直接值与规范值对比

综上所述，航行工况下，目标钻井船波浪弯矩的长期统计极值远大于规范计算值，两者之间的最大相对误差为34.61%，而最小相对误差为10.43%。由此可见，规范计算值不能作为钻井船的波浪载荷的设计值，对于此类工程型船舶必须进行波浪载荷直接计算。

3 结论

1)无论是采用长期预报法还是应用短期计算法来确定钻井船波浪弯矩设计值时，应对比分析同概率水平下波浪载荷的长短期预报极值，以增加计算结果的可靠性。

2)相同概率水平下，目标船波浪弯矩短期预报极值一般会大于长期预报极值。主要原因在于，两种方法对浪向处理方式不同。短期预报只考虑导致目标船波浪弯矩最恶劣的浪向，即顶浪浪向；而长期预报还会计及其他浪向的影响。

3)钻井船波浪弯矩的规范计算值比直接计算值小20%～30%，规范计算值不能作为目标船波浪弯矩的设计值。如果在前期输入条件不足的情况下，采用规范公式计算值时，建议乘以1.2～1.3的安全系数。