基于马氏距离的数据处理方法及其在高速公路改扩建工程定额中的应用

袁剑波，毛红日



基于马氏距离的数据处理方法及其在高速公路改扩建工程定额中的应用

袁剑波1,2，毛红日1

(1. 长沙理工大学 交通运输工程学院，湖南 长沙 410004； 2. 长沙理工大学 城南学院，湖南 长沙 410076)

针对高速公路改扩建定额编制中的数据处理，应用马氏距离法、2分布及分布，建立多元和单元的异常数据检测模型。将该模型应用于高速公路改扩建工程定额编制，减少干扰因素导致的实测数据的异常性，提高定额编制的精度，保证数据处理的科学性。

改扩建工程；马氏距离；卡方分布；分布；异常数据

高速公路改扩建工程与新建工程相比，更具复杂性，影响因素更多。相应地，定额原始数据的观测更困难，所观测的数据异常性更高。因此，编制高速公路改扩建定额时，需要科学、合理的原始数据处理方法。以检测原始数据中的异常数据，减少定额成果与现实情况的偏差。目前，异常数据的检测方法多为以下几种：莱茵达准则、狄克逊准则、格拉布斯准则、肖维勒准则以及罗马诺夫斯基准则(t检验)[1]。王首绪等[2]在新疆养护定额编制时采用t检验检测原始数据中的异常数据。QI等[3]采用修正格布拉斯法检测火电机组多个测试点异常性。王华等[4]在公路定额编制中采用格拉布准则检测异常数据[4]。以上方法主要是以欧氏距离为基础的检测。由于欧氏距离受量纲、变量相关性的影响[5−6]，该方法可以进一步通过马氏距离改进。理论上，马氏距离比欧氏距离、闵氏距离、兰氏距离更加优异[7]。马氏距离是一种距离度量方法，考虑了不同参数间的相关性，对各种参数间的变化敏感，由于使用归一化参数计算，它对所监控参数的不同量纲不敏感[8]，已经用于诸如异常检测、模式识别和过程控制[9]，在其他行业已得到广泛应用[10−13]。而传统马氏距离在小样本数据检测中，常出现协方差非奇异，导致无法求得马氏距离。本文应用协方差∑的−逆∑+的改进马氏距离，并结合卡方分布，建立了基于数组间的异常数据检测模型；马氏距离常应用于多元异常数据检测，为解决数据间的异常性，应用马氏距离与分布，建立了基于数据间的异常数据检测模型。因此，本文应用马氏距离法，结合统计分布的方法，从多元和单元的角度分析、处理数据，以达到减少实测数据中的异常性，提高定额精度的目的。

1 异常数据产生的原因

1.1 高速公路改扩建工程技术复杂性

高速公路改扩建工程中，应用路基拓宽、路面拼接、路面加铺及沥青再生、桥梁拆除、桥梁顶升、桥梁拼接等新技术。导致高速公路改扩建工程相比于新建公路，具有工作面不连续(较分散，有的为确保不中断交通需跳段施工)、工期长、成本高、施工风险高、施工环境复杂(施工干扰、交通组织等影响因素较多)等特点。因此，新技术的应用增长了原始数据观测时间、增加了原始数据观测的不连续性、增大了原始数据观测难度，同时缺乏相关经验及统计资料，导致异常数据产生的可能性更高。

1.2 观测的地理环境以及观测对象的差别

观测的地理环境以及观测对象的差别都可能导致所测定的原始数据出现较大的误差。高速公路改扩建相比新建公路，社会、人文和自然环境更加复杂，主要体现：高速公路改扩建工程是在原有高速公路基础上进行的，其附近经济走廊、管线工程已经形成，周围建筑物密集，导致工程变更量更大、工期更紧张、施工成本更高、前后工作紧密程度更低；高速公路改扩建采取边施工边通车原则，通车和施工并存，相互干扰，增加了施工工期、影响工序施工的连贯性；其他环境、社会因素也会高速公路改扩建施工过程造成干扰，进而影响观测数据的准确性。

1.3 检测者的原因

除去测量错误、读数错误、记录错误等检测者行为导致异常数据产生外，检测者对改扩建工程技术复杂性的认知水平也将导致异常数据产生，尤其是改扩建工程特有项目(新老路基拼接、桥梁拼接等)的施工工艺、施工方法和施工方案等方面认知水平的好坏，将导致观测数据的异常与否；改扩建工程现场情况复杂，合理的测时方法与合适的观测地点也会导致异常数据的产生。此外检测人员混乱、虚报、瞒报等原因也会导致原始数据的异常。

2 基于马氏距离的异常数据检测模型

2.1 马氏距离的定义

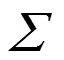
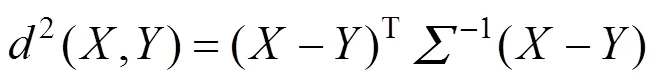
即马氏距离。

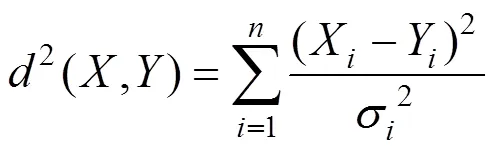
式中：σ为总体的标准差。

2.2 基于数组间异常的马氏距离检测模型

可以通过上述单位化数据来分析不同检测人员所观测数据间的差异度，差异度是描述两数组的相似程度。当差异度越小时，数组也就越接近，数组的异常性就越小。对于任意的2个检测人员的数组的马氏距离可用式(4)表示。

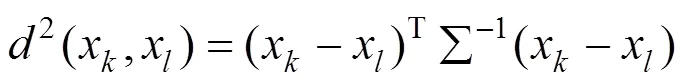
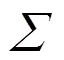
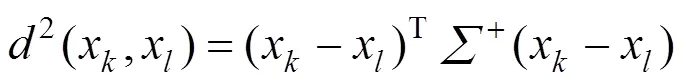
马氏距离是一种重要的多元异常数据检测的方法，是识别多元异常较好的综合指标，而马氏距离近似服从自由度为的卡方分布[19−20]，所以可以构建某个置信水平下的判别式(6)。

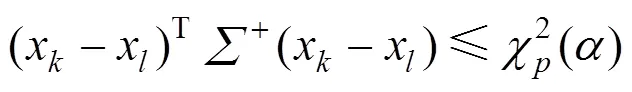
故最终判别式可为式(7)。

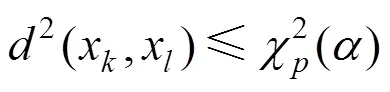
对于满足式(7)的数据，可认定数组间的差异度较小，不存在检测人员间受主、客观原因的影响。当数组不满足式(7)时，以多数原则选取合理的数组。

2.3 基于数据间异常的马氏距离检测模型

在考虑数组间的差异度后，也要考虑随机误差和系统误差等所引起的数据的异常性，即对满足式(7)的数组进行数据间的异常性检测。马氏距离多应用于多元异常数据的检测，为对单个测定值异常性作出判断，首先目的是构建数据间异常性检测的马氏距离模型，进而确定异常性检测的判别式。

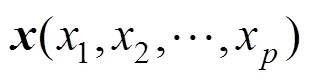
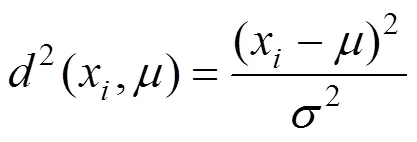
根据式(8)分析，以马氏距离构造统计量，见 式(9)。

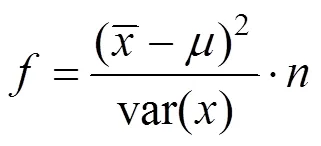
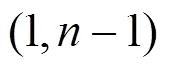
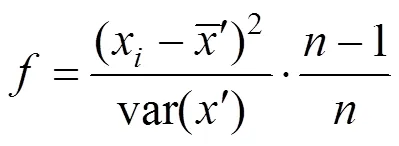
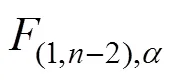
成立。

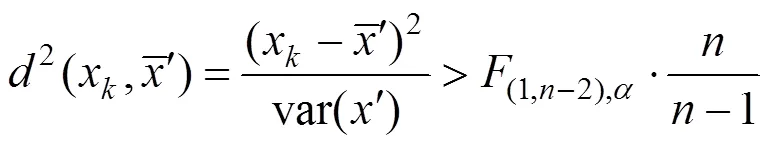
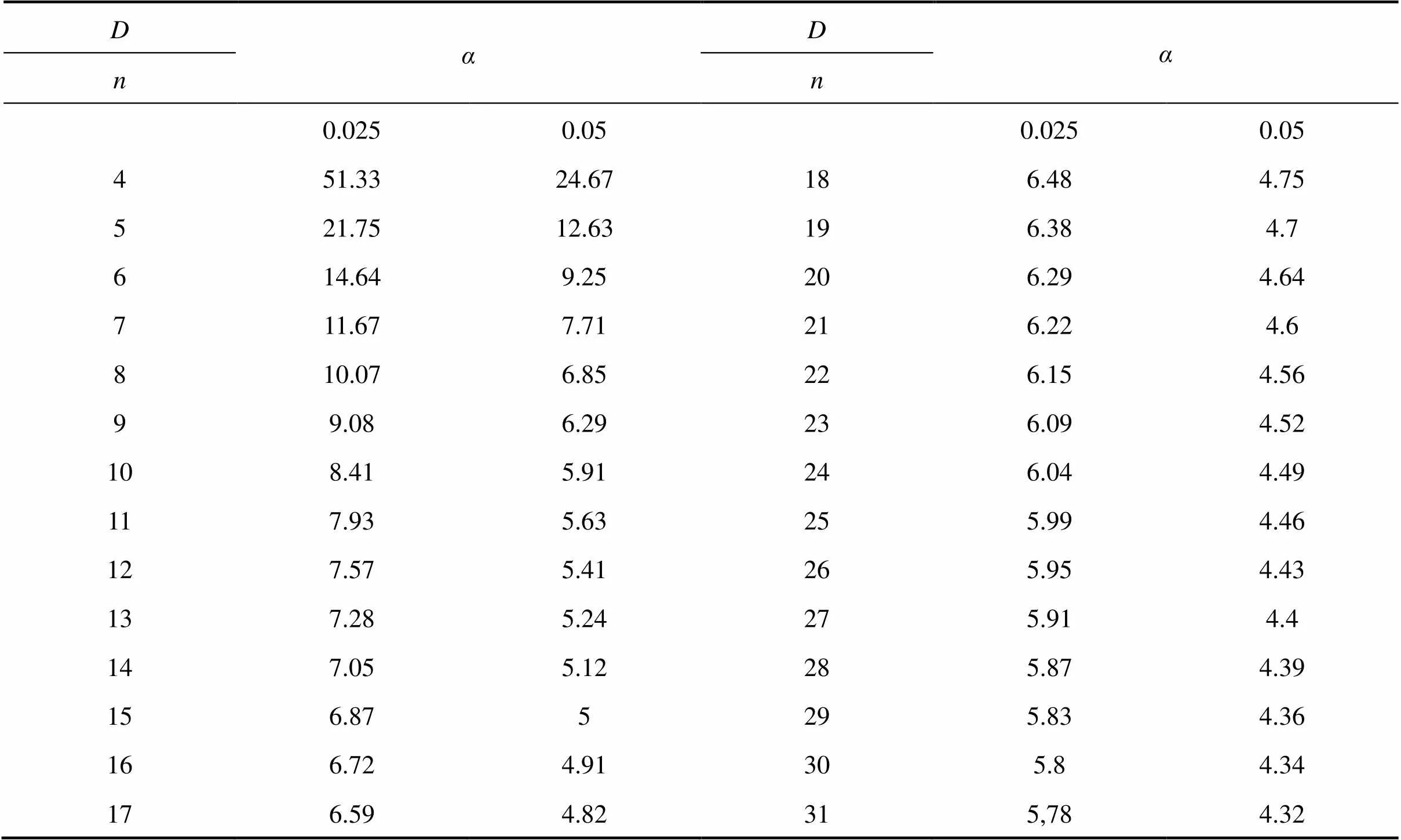
表1 准则参数M(n,α)

3 基于马氏距离模型的异常数据检测方法

3.1 数组间异常性的检测

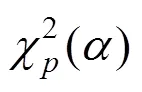
3.2 数据间异常性的检测

1) 多元数据的一元化，在个实测值中找到相对平均值偏差最大的观测值x，作为可疑数据；

2) 对不包括可疑数据x在内的(−1)个观测值，计算平均值以及样本方差；

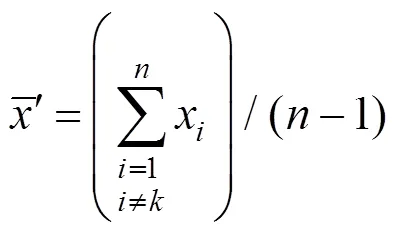
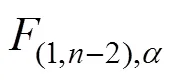
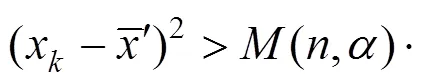
5) 如果x为异常数据，采用各种方法进行处理，然后对剩下的(−1)个观测数据按上述步骤进行检测，直至观测数据中不再有异常值。

4 实例分析

在高速公路改扩建定额编制中，不同的检测人员以工作日写实法观测“汽车吊吊梁”。其工作内容为：平板车运梁，人工绑扎吊绳，起吊、移位、定位和焊接等工作。观测数据以式(3)单位化，得到机械台班产量数据如表2。

表2 定额实测某工序中机械台班产量数据

1) 检测数组间的异常性，两两组合有3种情况(1,2)，(1,3)和(2,3)，并计算彼此的马氏距离。通过matlab编程[18]计算，结果如表3。

表3 数组间马氏距离

2) 单个数据的异常性检测，先将上述3个记录员的数据向量整理成一元的数据向量(从小到大)，如表4。

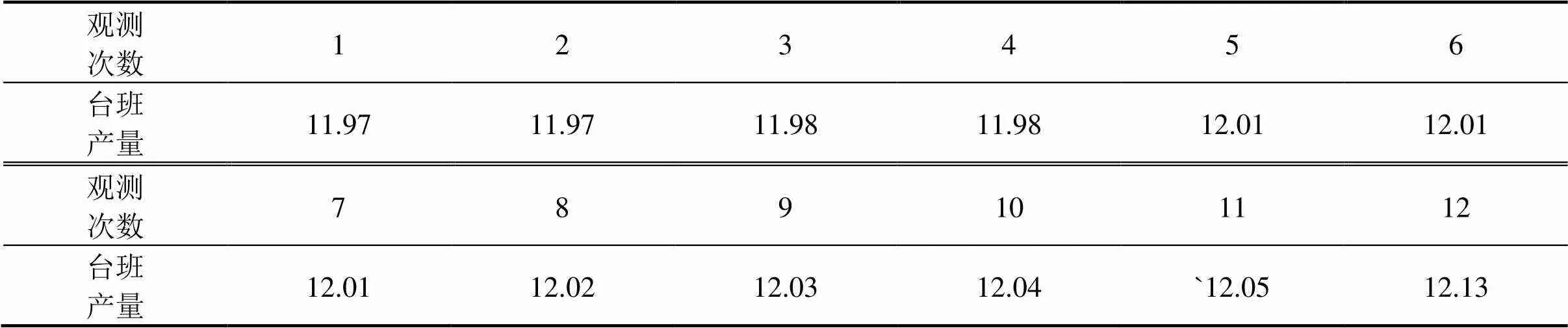
表4 定额实测某工序中机械台班产量数据

根据上述-准则的判别步骤，可以计算数据间的马氏距离如表5，表中主要是列出了检测到两端可疑点。

表5 数据间的马氏距离

根据上述表格中的单个数据间的马氏距离，通过查表1可以得到1,8是正常数据，而9是异常数据，从而对于异常数据予以处理(剔除、替换等)。

5 结论

1) 高速公路改扩建工程异常数据处理需从多元和单元的角度出发，综合考虑数组和数据间的异常性，通过减少干扰因素的影响提高定额的准确度。

2) 应用马氏距离法和2分布，构建了多元异常数据检测模型，考虑了多元样本间的相关性，排除了变量之间的不同量纲干扰。应用马氏距离法和分布，构建了单元异常数据检测模型，确定了不同的置信水平下和观测次数的准则参数值。

3) 从实例应用结果分析，多元检测过程中未检测到异常性，而在单元检测中检测到了异常数据。说明多元检测弱化了数据间的关系，主要考虑因素间联系，而单元检测主要考虑数据间的关系，忽略了多因素的影响，多元和单元双重检测下减少了异常性，提高了定额编制的精度。

[1] 费业泰. 误差理论与数据处理[M]. 北京: 机械工业出版社, 2004. FEI Yetai. Error theory and data processing[M]. Beijing: Mechanical Industry Press, 2004.

[2] 王首绪, 龙琰, 郭四泽. 基于t分布理论的公路定额数据小样本容量的收敛条件[J]. 长沙理工大学学报(自然科学版), 2007(2): 13−15, 20. WANG Shouxu, LONG Yan, GUO Size. Convergence condition of individual sample size about data among the road quota based on the theory of student distribution[J]. Journal of Changsha University of Science and Technology (Natural Science), 2007(2): 13−15, 20.

[3] QI Minfang, FU Zhongguang, CHEN Fei. Outliers detection method of multiple measuring points of parameters in power plant units[J]. Applied Thermal Engineering, 2015, 85(7): 297−303.

[4] 王华, 乔鹏. 公路定额测定异常数据剔除方法研究[J]. 中外公路, 2013, 33(6): 354−356. WANG Hua, QIAO Peng. Study on the method of eliminating abnormal data of highway quota[J]. Journal of China & Foreign Highway, 2013, 33(6): 354−356.

[5] 黄飞, 周军, 卢晓东. 基于马氏距离的一维距离像识别算法仿真[J]. 计算机仿真, 2010, 27(3): 31−34, 84. HUANG Fei, ZHOU Jun, LU Xiaodong. The simulation of one-dimensional range profile recognition based on Mahalanobis distance[J]. Computer Simulation, 2010, 27(3): 31−34, 84.

[6] 吴香华, 牛生杰, 吴诚鸥, 等. 马氏距离聚类分析中协方差矩阵估算的改进[J]. 数理统计与管理, 2011, 30(2): 240−245. WU Xianghua, NIU Shengjie, WU Chengou, et al. An improvement on estimating covariance matrix during cluster analysis using Mahalanobis distance[J]. Journal of Applied Statistics and Management, 2011, 30(2): 240− 245.

[7] Kumar S, Chow T W S, Pecht M. Approach to fault identification for electronic products using Mahalanobis distance[J]. IEEE Transactions on Instrumentation and Measurement, 2010, 59(8): 2055−2064.

[8] De Maesschalck R, Jouanrimbaud D, Massart D. The Mahalanobis distance[J]. Chemom Intell Lab Syst, 2000, 50(1): 1–18.

[9] 岳朝龙, 黄永兴, 严忠. SAS系统与经济统计分析[M].合肥: 中国科学技术大学出版社, 2003: 413−446. YUE Chaolong, HUANG Yongxing, YAN Zhong. SAS system and economic statistical analysis[M]. Hefei: University of Science and Technology of China Press, 2003: 413−446.

[10] 韩涵, 王厚军, 龙兵, 等. 基于改进马氏距离的模拟电路故障诊断方法[J]. 控制与决策, 2013, 28(11): 1713−1717, 1722. HAN Han, WANG Houjun, LONG Bing, et al. Method for analog circuit fault diagnosis based on improved Mahalanobis distance[J]. Control and Decision, 2013, 28(11): 1713−1717, 1722.

[11] Patil Nishad, Das Diganta, Pecht Michael. Anomaly detection for IGBTs using Mahalanobis distance[J]. Microelectronics Reliability, 2015, 55(7): 1054−1059.

[12] Penny Kay I. Appropriate critical values when testing for a single multivariate outlier by using the Mahalanobis distance[J].Journal of the Royal Statistical Society, Series C: Applied Statistics, 1996, 45(1): 73.

[13] Jaffel I, Taouali O, Faouzi Harkat M, et al. A fault detection index using principal component analysis and Mahalanobis distance[J]. IFAC-Papers on Line, 2015, 48(21): 1397−1401.

[14] Mahalanobis Prasanta Chandra. On the generalised distance in statistics[J]. Proceedings of the National Institute of Sciences of India, 1936, 2(1): 49–55.

[15] Gnanadesikan R, Kettenring J R. Robust estimates, residuals, and outlier detection with multiresponse data[J]. Biometrics, 1972, 28(1): 81−124.

[16] 交通部公路工程定额站. 公路工程定额的编制与管理[M]. 北京: 人民交通出版社, 2001. Ministry of Transportation Highway Engineering Quota Station. Construction and management of highway engineering quota[M]. Beijing: People’s Transportation Press, 2001.

[17] 陈欢, 黄德才. 基于广义马氏距离的缺损数据补值算法[J]. 计算机科学, 2011, 38(5): 149−153. CHEN Huan, HUANG Decai. Missing data imputation based on generalized Mahalanobis distance[J]. Computer Science, 2011, 38(5): 149−153.

[18] 曹慧荣, 张宝雷. 协方差阵奇异时马氏距离的一种改进[J]. 数学的实践与认识, 2015, 45(1): 226−230. CAO Huirong, ZHANG Baolei. An improvement definition of Mahalanobis distance with singular covariance matrix[J]. Mathematics in Practice and Theory, 2015, 45(1): 226−230.

[19] 王斌会, 陈一非. 基于稳健马氏距离的多元异常值检测[J]. 统计与决策, 2005(6): 4−6. WANG Binhui, CHEN Yifei. Multivariate anomaly detection based on robust Mahalanobis distance[J]. Statistics & Decision, 2005(6): 4−6.

[20] 陈永良, 路来君, 李学斌. 多元地球化学异常识别的核马氏距离方法[J]. 吉林大学学报(地球科学版), 2014, 44(1): 396−408. CHEN Yongliang, LU Laijun, LI Xuebin. Kernel mahalanobis distance for Multivariate geochemical anomaly recognition[J]. Journal of Jilin University (Earth Science Edition), 2014, 44(1): 396−408.

(编辑 蒋学东)

The data processing method based on Mahalanobis distance and its application in highway reconstruction engineering quota

YUAN Jianbo1, 2, MAO Hongri1

(1. School of Traffic and Transportation Engineering, Changsha University of Science & Technology, Changsha 410004, China; 2. Chengnan College, Changsha University of Science & Technology, Changsha 410076, China)

The abnormal data detection model of multivariate and unit is established by applying the Mahalanobis distance, chi-square distribution and F-distribution to the data processing in the establishment of quota for highway reconstruction engineering. The model is applied to the establishment of quota for highway reconstruction engineering, which reduces the abnormality of measured data caused by interference factors, improves the accuracy of quota establishment, and ensures the scientificity of data processing.

reconstruction project; Mahalanobis distance; Chi-square distribution;distribution; abnormal data

10.19713/j.cnki.43−1423/u.2018.10.035

U415.13

A

1672 − 7029(2018)10 − 2715 − 06

2017−08−27

国家自然科学基金资助项目(51578080)

袁剑波(1964−)，男，湖南益阳人，教授，博士，从事工程经济、项目管理研究；E−mail：yuanjb01@163.com