基于图参数估计法和IPSO的地铁列车关键设备检修决策模型研究

葛超，贺德强，谭文举



基于图参数估计法和IPSO的地铁列车关键设备检修决策模型研究

葛超1，贺德强1，谭文举2

(1. 广西大学 机械工程学院，广西 南宁 530004； 2. 南宁轨道交通集团有限责任公司广西 南宁 530029)

为了提高地铁列车关键设备检修决策能力，建立服从三参数威布尔分布，利用图参数估计法和IPSO算法求解可靠度函数，从而达到优化修规程目的的检修决策模型。通过图参数估计法求解得到故障数据的三参数威布尔分布初始估计值和搜索空间；采用IPSO算法进行迭代计算获得最优参数，并进行K-S检验；结合可靠度衍变规律和故障数据对关键设备的检修决策进行优化。研究结果表明：提出的决策模型能够优化关键设备的修规程，且IPSO算法适用于解决三参数威布尔参数估计问题，为地铁列车关键设备的检修提供新的方法。

地铁列车；检修；图参数估计法；IPSO算法；可靠性；三参数威布尔分布

地铁列车是城市轨道交通的重要装备，为了安全完成运输任务，必须使列车设备处于良好的技术状态。地铁列车每运行一段时间或相应里程后会执行检修工作，以恢复故障设备的功能，保证正线运营。以可靠性为中心的维修[1](RCM)提高了维修工作的针对性和效率，受到学术界的关注。马亮等[2]提出了一种地铁车辆预防性检修多目标优化模型和求解算法，提高了地铁车辆检修工作的效率；王红等[3]提出了一种基于维护方式多样性的地铁列车设备预防性维护决策模型，该模型能够制定合理的维护计划，降低维护成本；吕德峰等[4]建立了地铁车辆系统检查周期变化的检查优化模型，车辆可用度和检修经济性得以提高；孙超等[5]针对城市轨道交通车辆设备维修模式的不足，提出了基于可靠度的最佳维修周期确定方法，该方法未使用优化算法求解分布参数。夏军等[6]通过可靠性分析确定了地铁车门系统危害较大的故障模式，但未提出具体的车门检修优化方法。王莹等[7]基于列生成算法，根据动车组运用维修规程特点，建立了动车组检修计划优化模型；王灵芝等[8]研究了基于RCM的多部件成组预防性维修策略，建立了对应的维修费用优化模型；Doostparast等[9]研究了系统衰退设备的预防性维护问题，以保持可靠性及降低维修费用为目标提出了维修优化模型；Tsai等[10]研究了基于可用度的多部分系统的预防性维护，提出了可靠度模型，该模型基于可靠度最大优化维修时间间隔。目前，关于地铁列车RCM的研究相对较少，针对列车关键设备检修的研究更是罕见。为此，本文提出一种新的检修决策模型，该模型假设设备故障规律服从三参数威布尔分布，利用图参数估计法和IPSO算法求解最优参数并进行K-S拟合优度检验，从而得到故障设备的可靠度模型，结合可靠度衍变规律和故障检修数据对地铁列车关键设备的检修进行优化，为地铁列车检修科学决策提供依据。

1 三参数威布尔分布函数及其似然函数

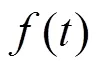
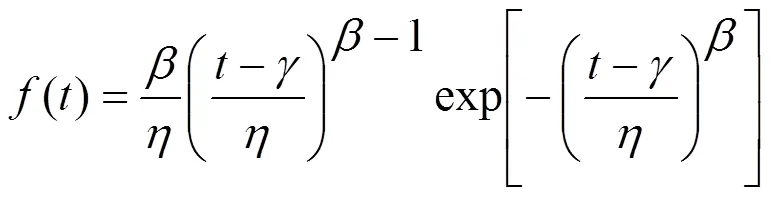
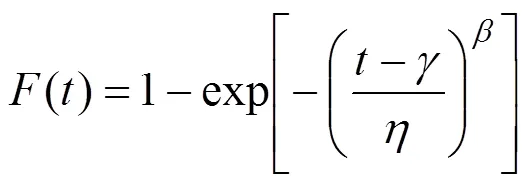
由式(1)可得样本的似然函数为

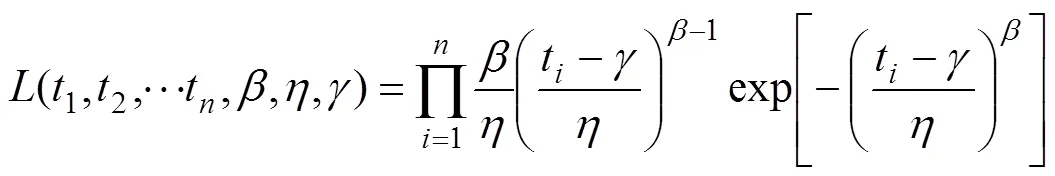
对式(4)取自然对数后可得：

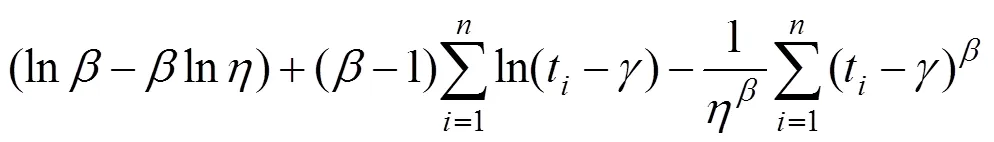
2 参数估计与假设检验法

2.1 图参数估计法

图参数估计法是三参数Weibull分布参数估计常用的方法，具有简单、直观、方便等优点。本文利用图参数估计法为算法提供解的初始估计值以及搜索空间。

对式(3)进行2次自然对数变换后转换为：

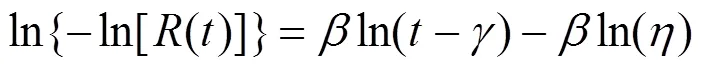
三参数威布尔分布利用图参数估计法估计参数的步骤如下：

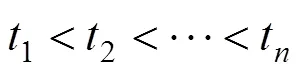
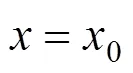
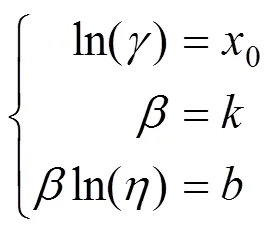
求方程组(7)可得基于图参数估计法的威布尔分布3个参数的估计值分别为：

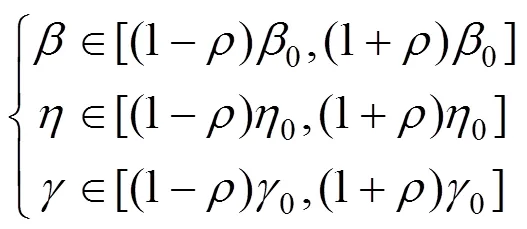
2.2 IPSO算法

基本PSO(Particle Swarm Optimization)算法是一类随机优化进化算法，其核心思想是模拟鸟群觅食的社会行为，通过鸟之间的竞争与协作在飞行空间中寻得食物，即寻找最优解的过程[12−13]。该算法由于具有较少的可调参数，易编程实现等特点，得到了深入的研究和广泛应用。

IPSO(Improved Particle Swarm Optimization)算法在基本PSO算法的基础上引入先进的理论，极大地提高了算法的收敛性、全局寻优性及收敛速度等性能。带时变惯性权重的IPSO算法能够控制算法的探测和开发能力，影响到全局和局部寻优性。

本文采取的IPSO算法进化方程为：

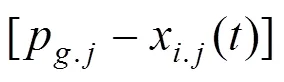
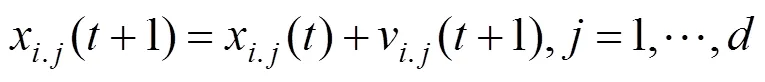
式中：1和2为加速常数；1和2为服从[0,1]区间均匀分布的随机数；为粒子序数；为当前迭代步数；为目标搜索空间的维数；x()为第步时第个粒子所处的位置；v()为第步时第个粒子的进化速度；p为第粒子历史最优适应度位置；p为全体粒子历史最优适应度位置；为惯性权重。

2.3 K-S拟合优度检验

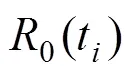
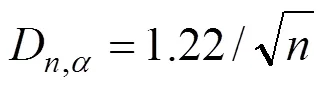
3 地铁列车关键设备算例分析

3.1 关键设备及其故障数据

地铁列车一般被分成多个子系统，各个子系统下包含一系列设备，其中故障频率较高和故障后果严重的为“关键设备”，应当是检修工作的重点。本文以南宁轨道交通1号线全部列车故障检修数据为研究对象。1号线运营工作由30列B2型车承担，该列车共有13个子系统，即：供风与制动、转向架、车门、车钩、贯通道、空调、车体及内装、牵引/制动、乘客信息、列车通信控制、主电路、照明子、辅助系统。对2016−03~2017−03(含试运营)30列列车的故障数据进行整理和统计，统计结果如图1所示，发现在全部子系统中，车门系统的故障次数占比(子系统故障次数/所有子系统故障次数之和)最高达17%，说明车门系统具有较高的故障率。线上营运列车车门出现故障很可能造成列车延误、掉线甚至严重的安全事故，影响乘车人的舒适度和人身安全。

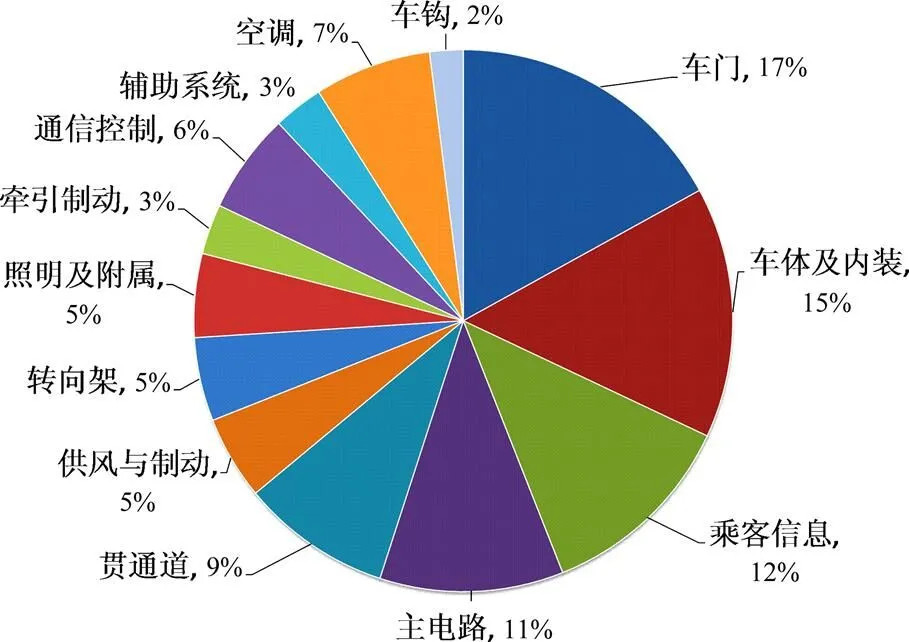
图1 各子系统故障数据统计

本文选择以客室车门关键设备的运营故障记录为故障样本，进行可靠性分析。根据故障数据，选取故障次数较多的设备进行统计，结果如图2 所示。

由图2可见，平衡压轮和门控器发生故障最为频繁，选择其为客室车门的关键设备，下面以这2种设备为例进行分析，检验上述决策模型的有效性。对平衡压轮压力和门控器的故障数据进行图参数估计初步计算的结果如表1和表2所示。

图2 客室车门故障统计

表1 平衡压轮故障数据

Table 1 Fault data of balance pressure wheels

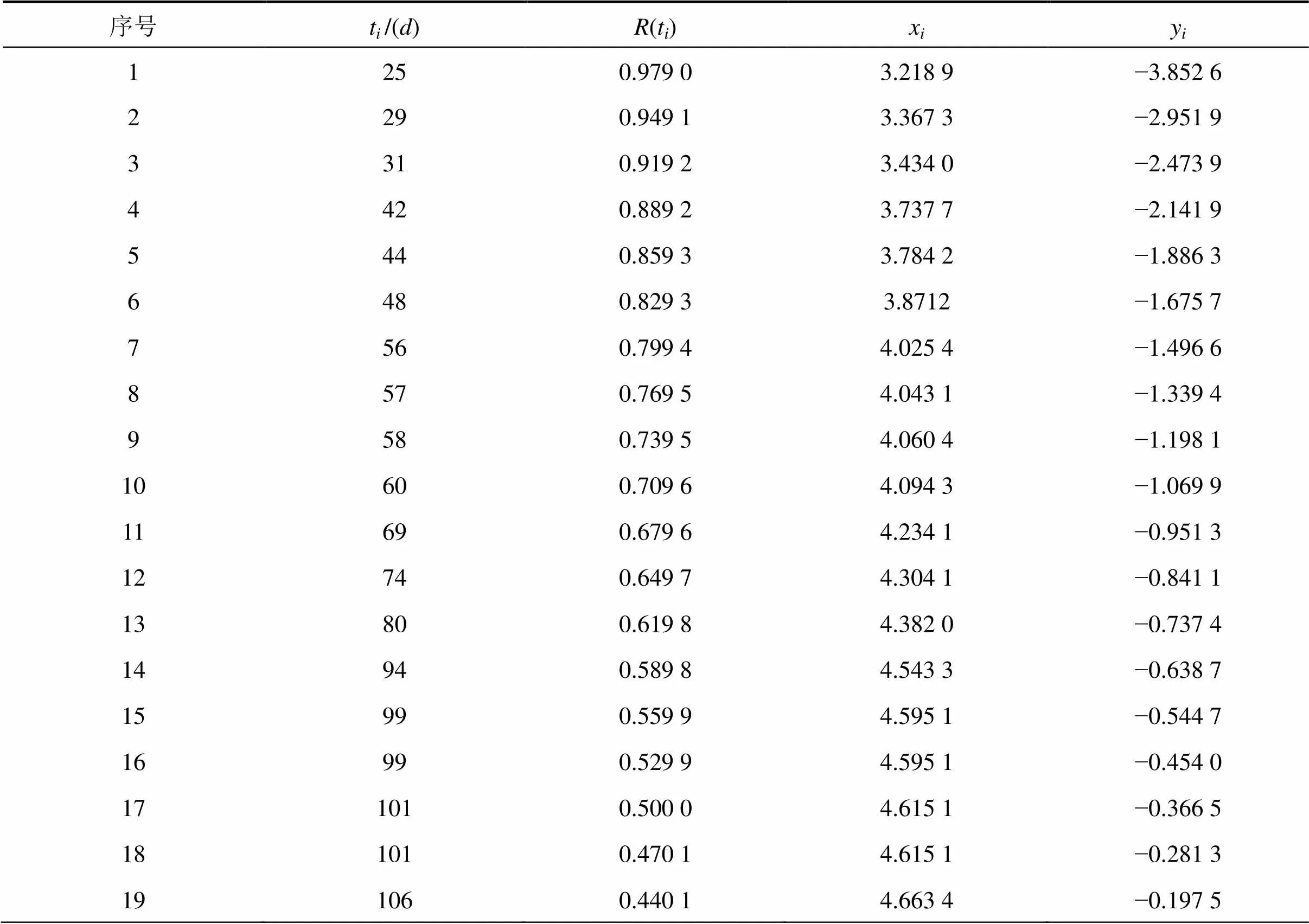
序号ti /(d)R(ti)xiyi 1250.979 03.218 9−3.852 6 2290.949 13.367 3−2.951 9 3310.919 23.434 0−2.473 9 4420.889 23.737 7−2.141 9 5440.859 33.784 2−1.886 3 6480.829 33.8712−1.675 7 7560.799 44.025 4−1.496 6 8570.769 54.043 1−1.339 4 9580.739 54.060 4−1.198 1 10600.709 64.094 3−1.069 9 11690.679 64.234 1−0.951 3 12740.649 74.304 1−0.841 1 13800.619 84.382 0−0.737 4 14940.589 84.543 3−0.638 7 15990.559 94.595 1−0.544 7 16990.529 94.595 1−0.454 0 171010.500 04.615 1−0.366 5 181010.470 14.615 1−0.281 3 191060.440 14.663 4−0.197 5

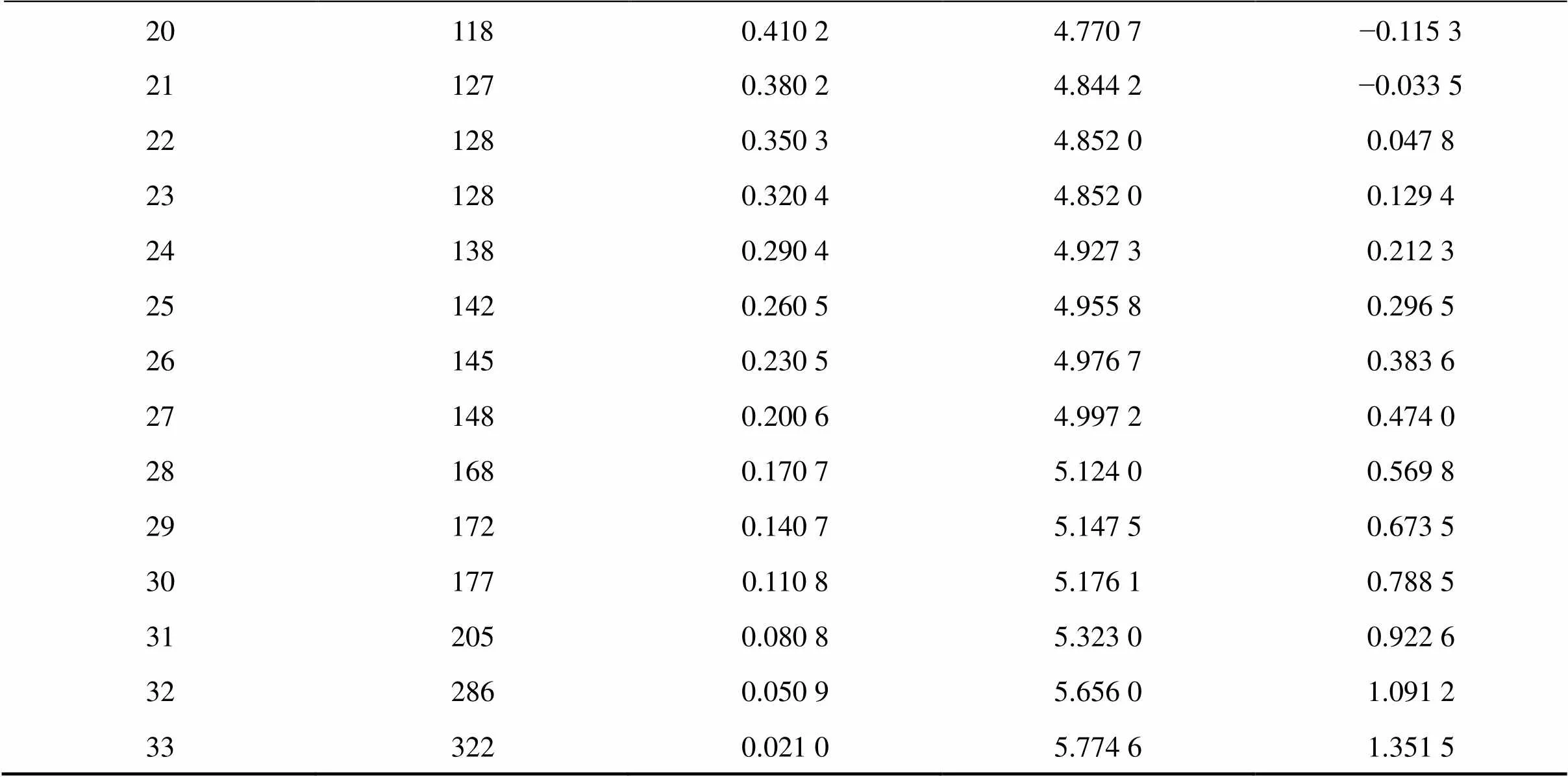
201180.410 24.770 7−0.115 3 211270.380 24.844 2−0.033 5 221280.350 34.852 00.047 8 231280.320 44.852 00.129 4 241380.290 44.927 30.212 3 251420.260 54.955 80.296 5 261450.230 54.976 70.383 6 271480.200 64.997 20.474 0 281680.170 75.124 00.569 8 291720.140 75.147 50.673 5 301770.110 85.176 10.788 5 312050.080 85.323 00.922 6 322860.050 95.656 01.091 2 333220.021 05.774 61.351 5

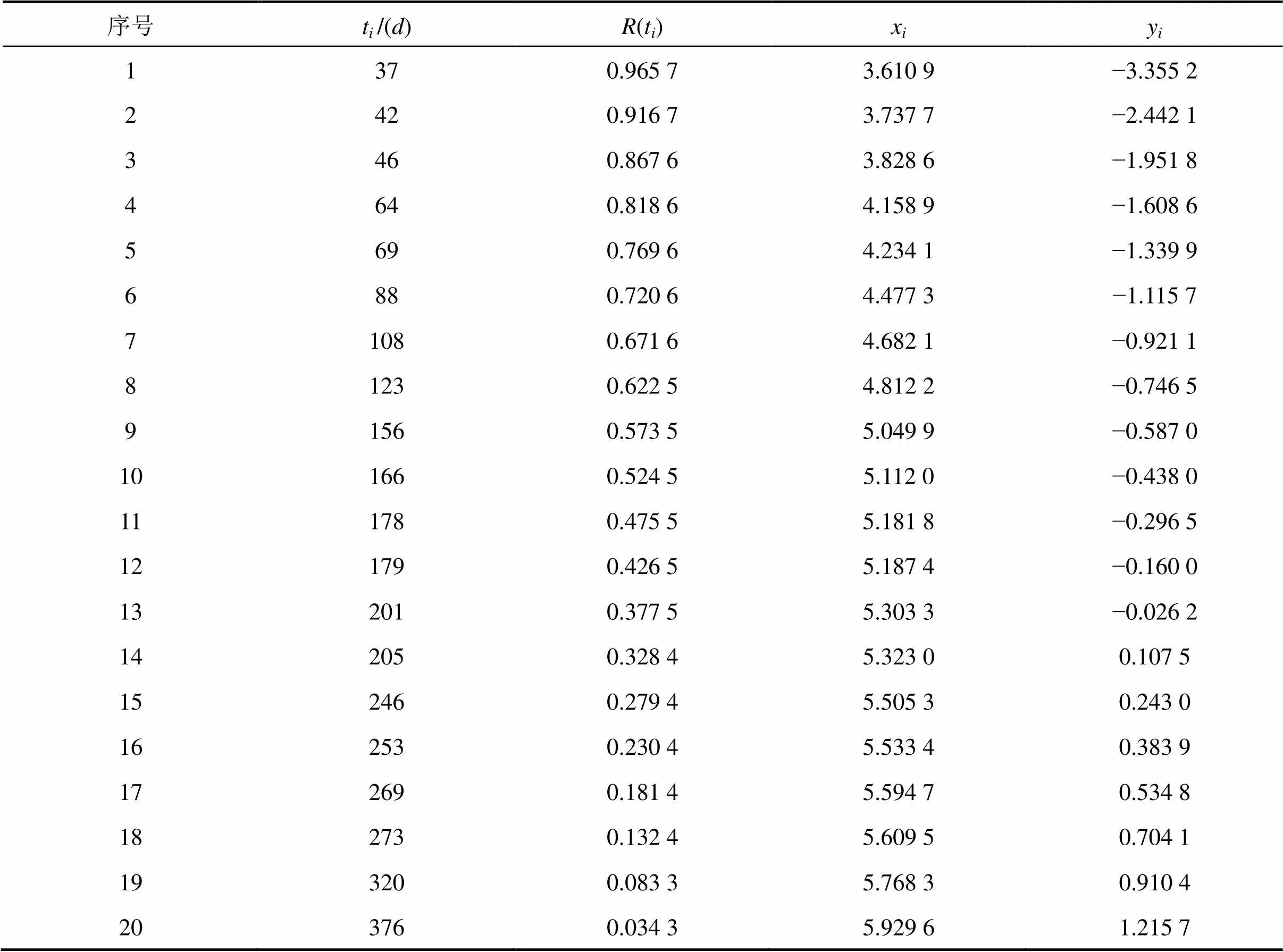
表2 门控器故障数据

3.2 参数求解和假设检验

根据表1和表2，绘制故障数据的散点图，如图3和图4所示。

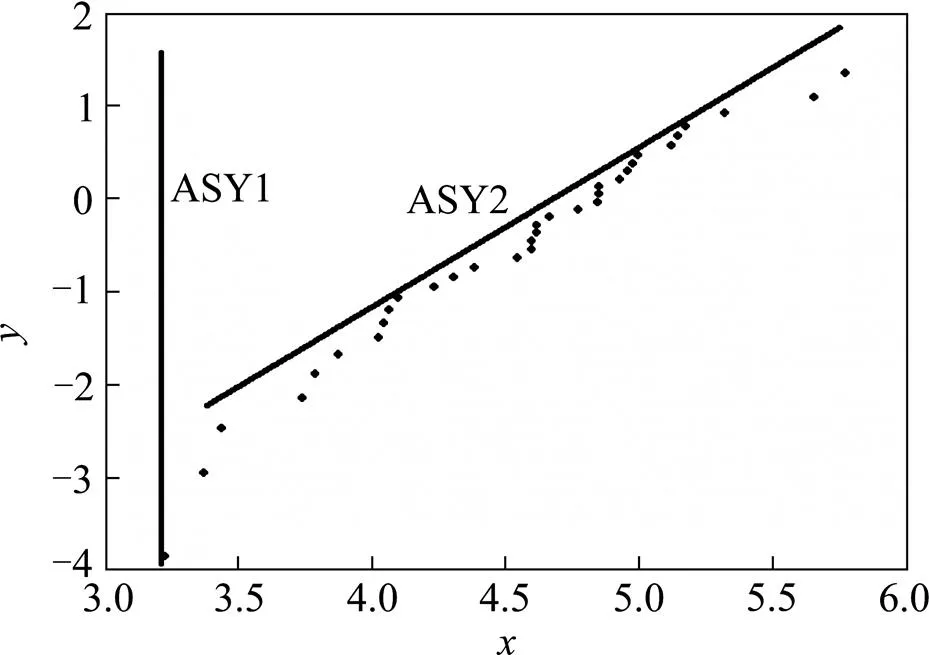
图3 平衡压轮的故障数据WPP及渐近线图

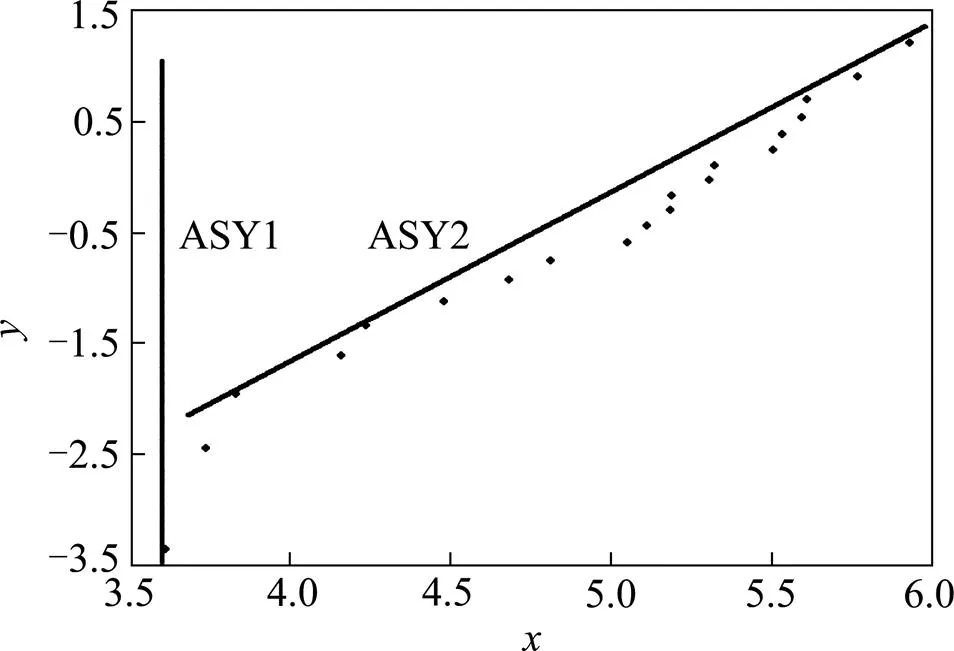
图4 门控器的故障数据WPP及渐近线图

分析图3和图4，发现散点并非分布于同一条直线，而是呈曲线波动状，且存在明显的拐点，即存在显著的凹凸性变化，这与三参数威布尔分布的特征相契合。由此可以假定故障数据符合三参数威布尔分布。在图3和4中作直线ASY1和ASY2，分别为散点的铅垂渐近线和斜渐近线。通过拟合计算得到平衡压轮和门控器的渐进线方程：

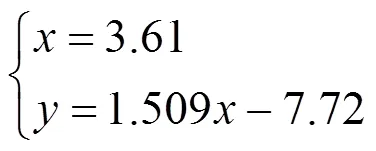
方程组(13)为平衡压轮的渐近线，方程组(14)为门控器的渐近线。

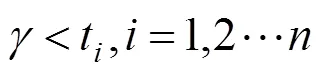
平衡压轮故障数据的初始估计值及搜索空间为：

门控器故障数据的初始估计值及搜索空间为：

根据IPSO算法编写程序对目标函数进行迭代寻优计算，得到平衡压轮和门控器的迭代过程，如图5和6所示。

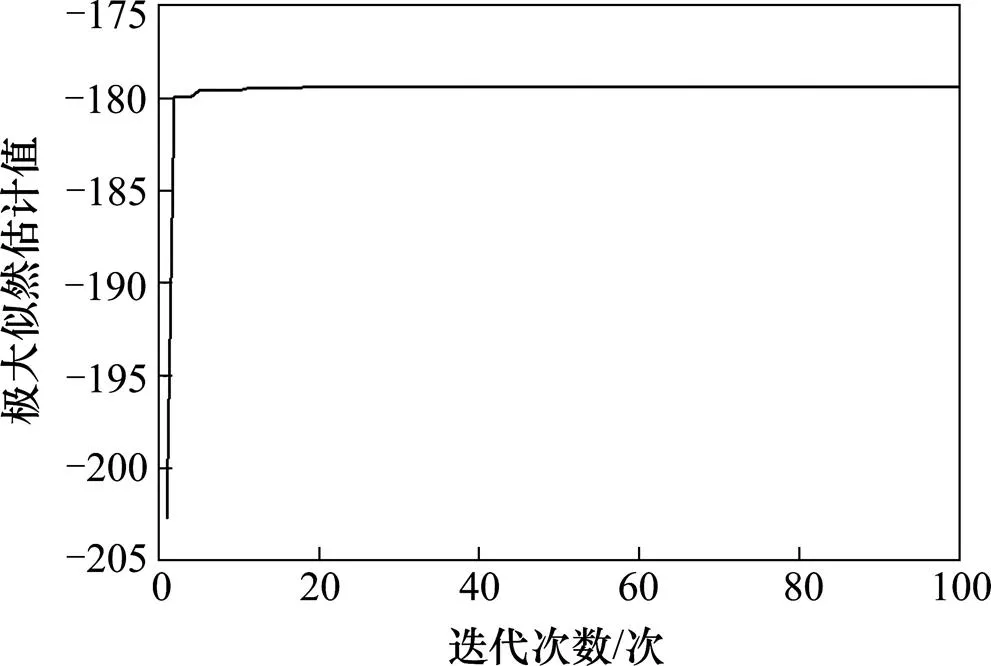
图5 平衡压轮的迭代寻优结果

IPSO算法的具体求解流程如图7所示。

算法中各参数取值如下：加速常数1和2都取2；目标搜索空间的维数取3；迭代次数取100；惯性权重采用线性递减方式，最大值和最小值分别为0.9和0.6；粒子数为40。

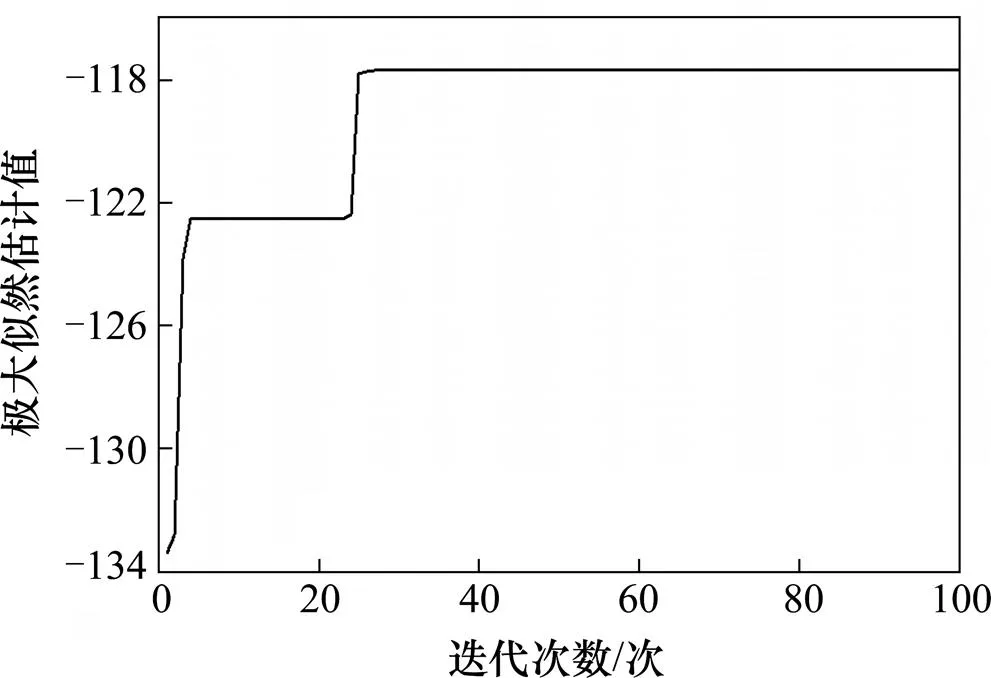
图6 门控器的迭代寻优结果

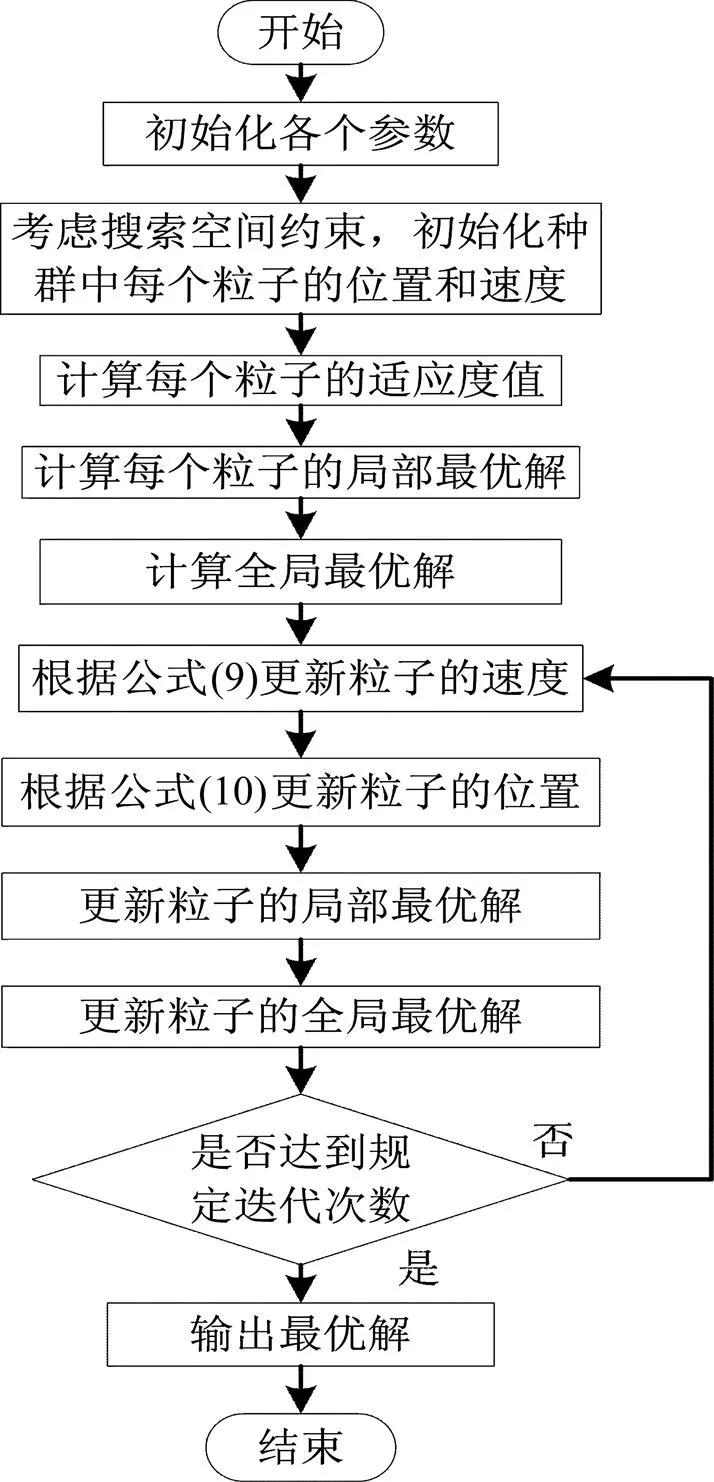
图7 IPSO算法具体流程

平衡压轮K-S检验结果：

门控器K-S检验结果：

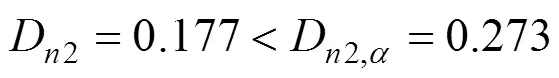
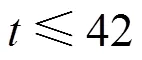
从式(15)及(16)可以看出，检验条件完全成立，因此可以判定平衡压轮和门控器的故障时间间隔服从三参数威布尔分布。

由式(3)得：

平衡压轮可靠度函数如下：

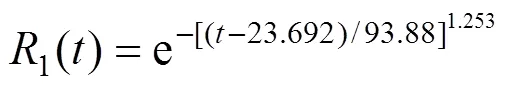
门控器可靠度函数如下：

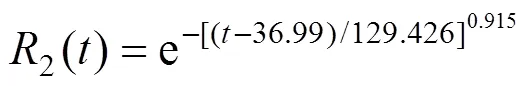
根据可靠度函数和故障数据，在同一张图中绘制可靠度衍变曲线，如图8~9所示。

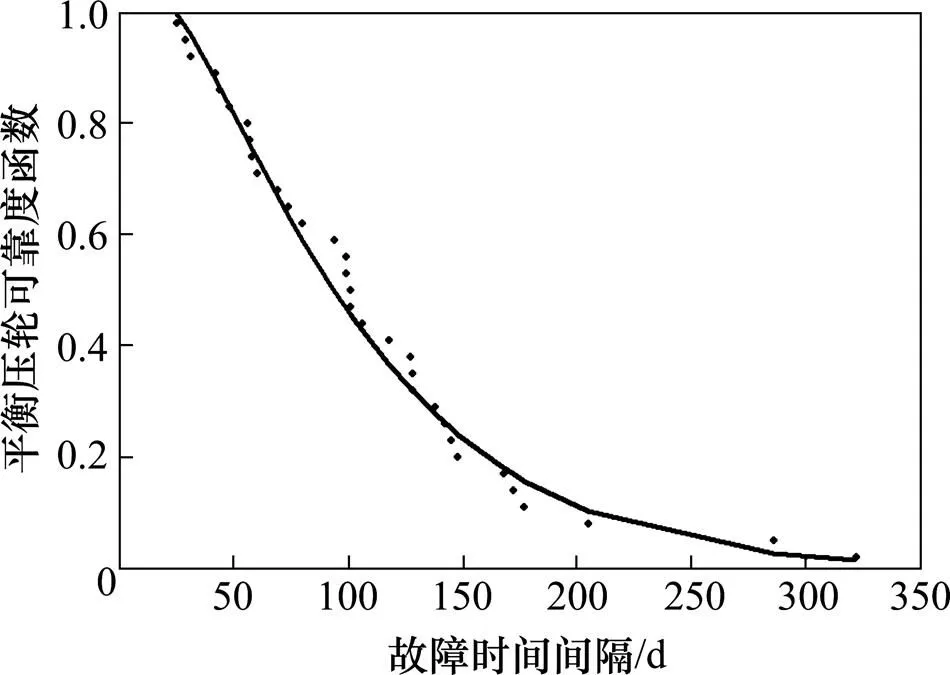
图8 平衡压轮故障间隔时间可靠度函数图

3.3 计算结果分析

分析图8~9，发现实际故障数据均匀分布于可靠性函数曲线的两侧，且变化趋势相同。门控器拟合图中的某些故障点的拟合效果较差，与人为检修误差影响了数据精度有关。总体来看，这进一步证明了地铁列车关键设备的故障时间间隔分布规律与三参数威布尔分布相吻合，同时也表明本文提出的决策模型有效。

可靠度是衡量设备在规定条件下实现预定功能能力的重要指标，并且二者之间呈正比例关系。保证设备维持在高可靠度重要手段就是进行高效的预防性定期检修，因此，必须考量检修策略的合理性。

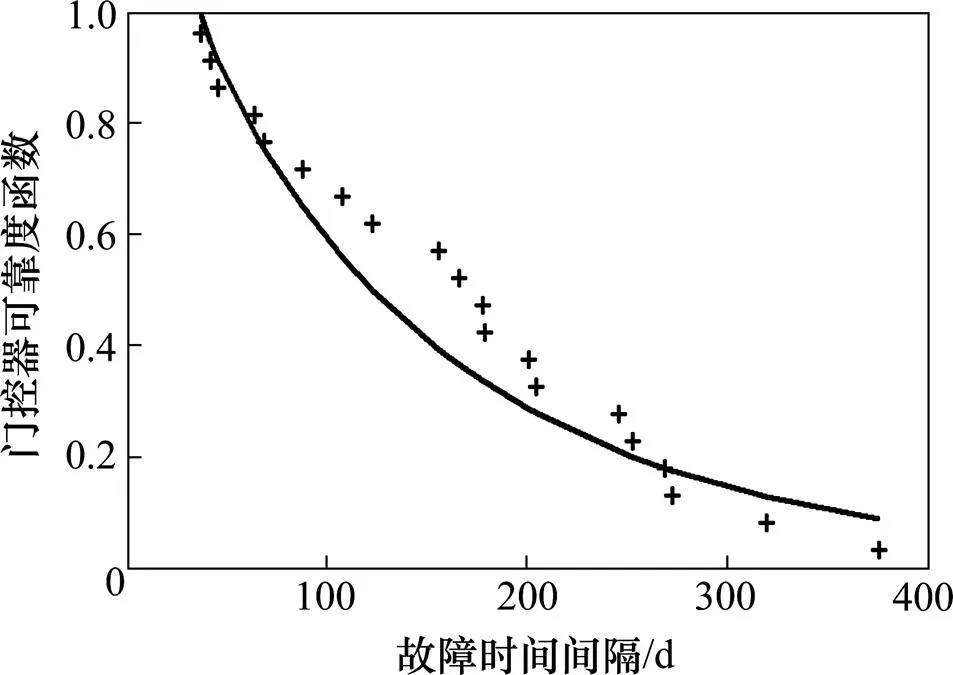
图9 门控器故障间隔时间可靠度函数图

本文从平衡压轮和门控器的可靠度衍变规律和故障数据记录入手，结合当前的检修修程和规程，优化地铁列车关键设备的检修策略。平衡压轮和门控器检修内容如表3所示。

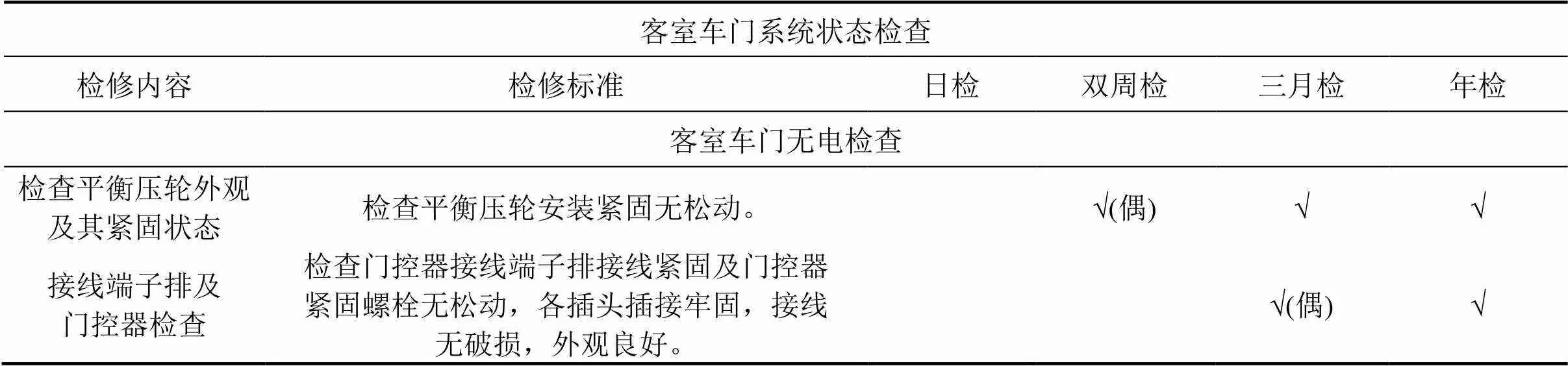
表3 平衡压轮和门控器检修内容

3.4 IPSO算法适用性分析

为了证明IPSO算法对于解决本文参数估计问题的适用性，选择使用另一种群优化算法IABC (Improved Artificial Bee Colony)算法对目标函数进行迭代寻优，所得的计算结果如图10~11所示。

图10 平衡压轮故障数据优化迭代结果

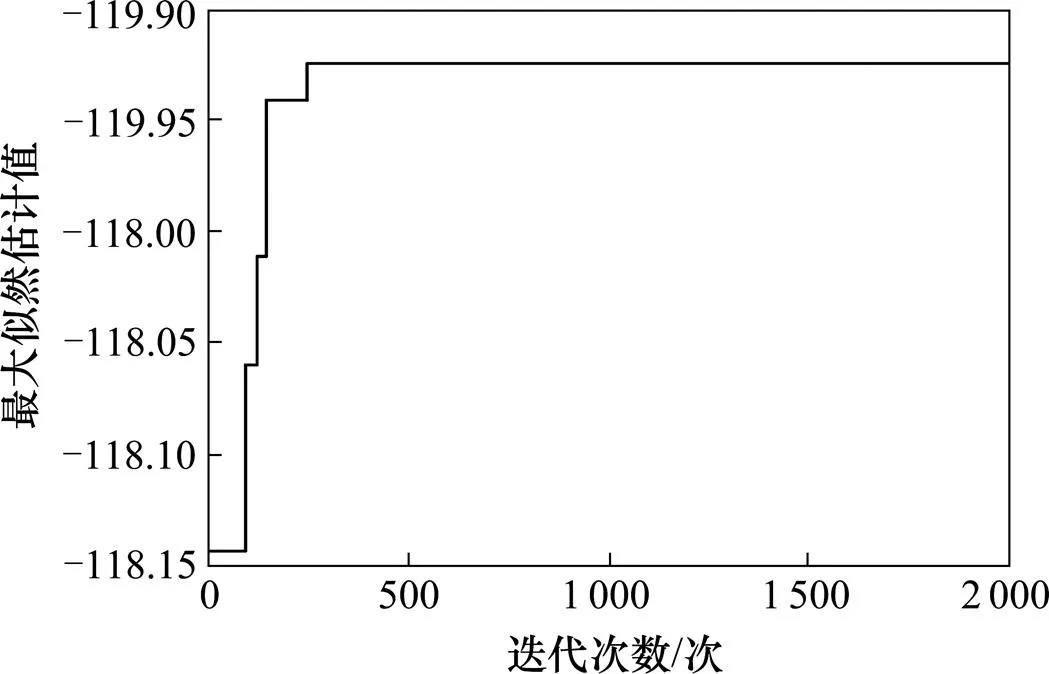
图11 门控器故障数据优化迭代结果

把2种算法的迭代过程和结果进行对比，结果如表4所示。从表中可以看出，2种算法的求解精度基本相同，但是在收敛速度上迥异。IPSO算法的收敛速度明显快于IABC算法，就平衡压轮的最快收敛迭代次数来看，二者相差34倍。同时，IPSO算法的收敛速度稳定，通过25~30次迭代即可得到最优解，而IABC算法收敛速度极不稳定，最快收敛迭代次数相差750次。较快的求解速度和稳定性得益于ISPO算法本身特点及算法参数的合理选择。因此，本文提出的IPSO算法用于解决本文的参数估计问题更具适用性。

表4 IPSO和IABC的迭代效果

4 结论

1) 三参数威布尔分布在设备寿命可靠性分析中具有重要意义，对于故障数据具有强大的拟合能力。结合图参数估计法和IPSO算法求解威布尔分布三个最优参数，进而得到故障设备的可靠度函数，建立起检修决策模型。

2) 分析实际地铁列车的故障数据，选取关键设备，并应用决策模型进行解算，验证了决策模型的有效性。通过算法对比，证明了IPSO算法适用于解决三参数威布尔参数估计问题。

3) 根据关键设备的可靠度模型和故障数据，对列车检修进行优化，证明了决策模型具有一定的实际应用价值，为地铁列车检修决策提供了新方法。

[1] 贾希胜. 以可靠性为中心的维修决策模型[M]. 北京:国防工业出版社, 2007. JIA Xisheng. The deision models for reliability centred maintenance[M]. Beijing: National Defence Industry Press, 2007.

[2] 马亮, 郭进, 张晓霞. 地铁车辆预防性检修计划优化模型与算法[J]. 铁道学报, 2016, 38(7): 8−14. MA Liang, GUO Jin, ZHANG Xiaoxia. Optimation model and algorithm of preventive maintenance schedule for metro rolling stock[J]. Journal of the China Railway Society, 2016, 38(7): 8−14.

[3] 王红, 刘志龙, 杜维鑫, 等. 基于多种维护方式的地铁车辆设备预防性维护策略及维护模型[J]. 中国铁道科学, 2016, 37(4): 108−114. WANG Hong, LIU Zhilong, DU Weixin, et al. Preventive maintenance strategy and model for metro vehicle equipment based on various maintenance methods[J]. China Railway Science, 2016, 37(4): 108−114.

[4] 吕德峰, 过秀成, 孔哲, 等. 基于可用度的地铁车辆维修检查间隔优化方法[J]. 东南大学学报(自然科学版),2011, 41(4): 877−881. LÜ Defeng, GUO Xiucheng, KONG Zhe, et al. Maintence inspection interval of metro vehicle based on availability[J]. Journal of Southeast University (Natural Science Edition), 2011, 41(4): 877−881.

[5] 孙超, 徐永能. 城市轨道交通车辆走行部维修周期优化模型[J]. 城市轨道交通研究, 2015, 31(1): 71−73. SUN Chao, XU Yongneng. Optimum maintenance circle model for rail transit vehicle’s running gear[J]. Urban Mass Transit, 2015, 31(1): 71−73.

[6] 夏军, 郭翔, 邢宗义, 等. 地铁车门系统故障模式可靠性分析[J]. 组合机床与自动化加工技术, 2014, 55(3): 49−52.XIA Jun, GUO Xiang, XING Zongyi, et al. Failure mode critically analysis of metro door system[J]. Modular Machine Tool & Automatic Manufacturing Technique, 2014, 55(3): 49−52.

[7] 王莹, 刘军, 苗建瑞. 基于列生成算法的动车组检修计划优化[J]. 中国铁道科学, 2010, 31(2): 115−120.WANG Ying, LIU Jun, MIAO Jianrui. Column generation algorithms based optimation method for maintenance scheduling of muitiple units[J]. China Railway Science, 2010, 31(2): 115−120.

[8] 王灵芝, 徐宇工, 张家栋. 以可靠性为中心的多部件系统预防性维修优化研究[J]. 计算机集成制造系统, 2008, 126(10): 2042−2046. WANG Lingzhi, XU Yugong, ZHANG Jiadong. Optimization of reliability-centered preventive maintenance for multi-component systems[J]. Computer Integrated Manufacturing Systems, 2008, 126(10): 2042−2046.

[9] Doostparast M, Kolahan F, Doostparast M. A reliability-based approach to optimize preventive maintenance scheduling for coherent systems[J]. Reliability Engineering & System Safety, 2014, 126(126): 98−106.

[10] Tsai Y T, Wang K S, Tsai L C. A study of availa- blity-centered preventive maintenance for multi- componet systems[J]. Reliability Engineering & System Safety 2004, 84(3): 261−270.

[11] 杨谋存, 聂宏. 三参数Weibull分布参数的极大似然估计数值解法[J]. 南京航空航天大学学报, 2007, 39(1): 22−25. YANG Moucun, NIE Hong. Advanced algorithm for maximum likelihood estimation of three parameter weibull distribution.[J]. Journal of Nanjing University of Aeronautics & Astronautics, 2007, 39(1): 22−25.

[12] Kennedy J, Eberhart R. Particle swarm optimization[C]// IEEE International Conference on Neural Networks, 1995. Proceedings. IEEE, 2002: 1942−1948.

[13] Eberhart R, Kennedy J. A new optimizer using particle swarm theory[C]// International Symposium on MICRO Machine and Human Science. IEEE, 2002: 39−43.

[14] 孙妍婷. 动车组关键零部件维修决策模型的研究[D]. 北京: 北京交通大学, 2012. SUN Yanting. The research on maintenance decision model of EMU key components[D]. Beijing: Beijing Jiaotong University, 2012.

[15] 麻晓敏, 张士杰, 胡丽琴, 等. 可靠性数据威布尔分析中秩评定算法改进研究[J]. 核科学与工程, 2007, 27(2): 152−155. MA Xiaomin, ZHANG Shijie, HU Liqin et al. An improved rank assessment method for Weibull analysis of reliability data[J]. Chinese Journal of Nuclear Science and Engineering, 2007, 27(2): 152−155.

(编辑 蒋学东)

Research on overhaul decision model of key equipment of metro train based on graph parameter estimation method and IPSO algorithm

GE Chao1, HE Deqiang1, TAN Wenju2

(1. College of Mechanical Engineering, Guangxi University, Nanning 530004, China; 2. Nanning Rail Transit Co., Ltd, Nanning 530029, China)

For the improvement of key equipment overhaul decision ability of metro trains, the graph parameter estimation method and IPSO algorithm are used to solve the reliability function, and the maintenance decision model which is subject to the three-parameter Weibull distribution is established, achieving the purpose of optimizing repair procedure. Graph parameter estimation method is first used to obtain the initial estimated value and the search space of three parameter Weibull distribution of fault data, then IPSO algorithm is used to get optimum parameters by iterative computation, and then K-S test is employed, at last, key equipment overhaul is optimized by combining evolution law of reliability with fault data. Simulation analysis of actual metro train fault data shows that the decision model can optimize the class of repairs and procedures of key equipment, IPSO algorithm is suitable to solve three parameter Weibull distribution parameter estimation problem and a new method is provided for the overhaul of metro train key equipment.

metro trains; overhaul; graph parameter estimation method; IPSO algorithm; reliability; three parameter Weibull distribution

10.19713/j.cnki.43−1423/u.2018.10.028

TP391.9；U279

A

1672 − 7029(2018)10 − 2661 − 09

2017−07−27

国家自然科学基金资助项目(51765006)；广西科技攻关资助项目(桂科攻1598009-6)；南宁市科技攻关资助项目(20151021)；广西制造系统与先进制造技术重点实验主任资助项目(15-140-30S003)

贺德强(1973−)，男，湖南桃江人，教授，博士，从事机车车辆故障诊断与智能维护、列车网络与控制、网络化制造研究；E−mail：hdqianglqy@126.com