基于抗差估计的BDS/ODO组合列车定位方法

蔡煊，王长林



基于抗差估计的BDS/ODO组合列车定位方法

蔡煊1，王长林2

(1. 西南交通大学 牵引动力国家重点实验室，四川 成都 610031； 2. 西南交通大学 信息科学与技术学院，四川 成都 610031)

根据列车定位的实际需求，采用北斗卫星导航系统和里程计构建列车组合定位系统，利用二者的优势进行互补。针对传统的Kalman滤波算法用于列车组合定位融合估计存在的问题，提出一种基于抗差估计理论的列车组合定位方法。对各传感器观测信息应用抗差估计进行融合解算，利用等价权函数自适应地调节各传感器观测值的比重，有效降低粗差观测值对融合结果的影响。研究结果表明：在传感器观测值含有粗差的情况下，基于抗差估计的组合定位解明显优于常规Kalman滤波解和扩展Kalman滤波解。抗差估计法能增强系统的鲁棒性，提高滤波实时性，保证列车定位的精确性和可靠性。

列车定位；组合定位；北斗卫星导航系统；里程计；抗差估计；等价权函数

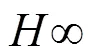
1 BDS/ODO组合定位

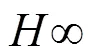
BDS是我国自主研发、独立运行的全球卫星导航系统，该系统与第3代GPS定位精度相当。BDS与GPS在导航定位原理、系统构置、星历数据结构、调制方式等方面基本相似，都是采用发射扩频测距码，测量接收机与导航卫星之间的伪距来实现导航定位。但相对于GPS，BDS系统具有空间混合星座、自带广域差分增强、导航定位与通信一体化等独特优势。目前，BDS已可为亚太地区提供功能完整的导航定位服务，2020年全面建成后可提供覆盖全球的精准定位、导航和授时(Positioning，Navigation and Timing，PNT)服务。作为我国具有自主控制权的卫星导航系统，扩大和深化BDS在我国交通、通信、国防等关键部门的应用具有极为重要的战略意义[17−18]。

本文根据北斗卫星导航系统和里程计的定位特性，构建基于BDS和ODO的列车组合定位系统，利用2种传感器的优势进行互补。里程计定位是一种典型的相对定位方式，只能测量相对于某一绝对位置的里程信息，无法确定列车的初始位置，传统方式大多依靠地面应答器或轨道电路为列车完成初始定位。而卫星定位是一种典型的绝对定位方式，可以连续确定运动载体的绝对位置，且其定位误差不累积，因此可利用BDS的绝对位置信息为ODO提供列车初始位置，以及利用BDS定位信息解算的运行里程不断修正ODO的里程累积误差，使其收敛至较低水平。采用BDS进行列车定位可对目前主流的里程计定位法进行有效补充，将列车定位系统主要建立在车载环境中，显著减少应答器等地面辅助设备，以较低的成本实现列车运行控制系统对列车定位的需求。

另外，BDS低频特性较好、高频特性较差，而ODO正好相反，利用ODO的高频输出可弥补BDS低频测量的不足和卫星信号受遮挡时无法准确定位的缺陷。当列车运行在平原等卫星信号较好的区域时，采用BDS/ODO组合定位方式；当列车运行于隧道、山区等卫星信号减弱或消失的区域时，采用ODO单独测速定位，保证列车定位的连续性，当重新接收到可靠的卫星信号时，利用BDS定位结果对ODO误差进行校正。可见，BDS和ODO具有良好的互补性，是一种较为理想的列车组合定位方案。

2 基于抗差估计的BDS/ODO组合定位融合算法

2.1 传感器定位解算

里程计通过记录车轮的累计转数，再结合轮径(车轮直径)值即可求得列车运行速度和里程。第周期，里程计测量的里程增量为：

根据里程增量可以得到列车运行速度：

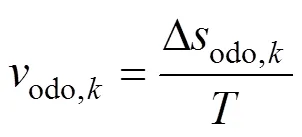
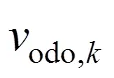
北斗卫星定位系统在测得每个周期的列车绝对位置信息后，可通过相邻周期的位置信息导出该周期内的列车里程增量：

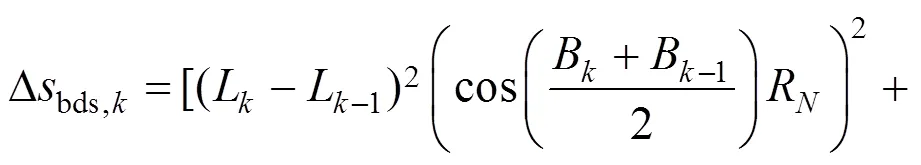
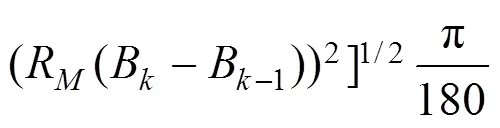
由于BDS采样周期较小，这段时间内的卫星钟差、星历误差等都很小，使得相邻周期的BDS定位结果具有较强相关性，由此导出的里程信息的误差一般小于定位误差。但在可视卫星数明显减少时，BDS里程观测值存在较大粗差。

2.2 基于抗差估计的融合解算

针对传统Kalman滤波估计存在的缺陷，本文提出一种基于传感器观测信息抗差估计的BDS/ ODO组合定位融合算法。抗差估计是一种既能抵制模型偏差又能抗拒异常观测值扰动的稳健估计法。该方法将抗差等价权函数引入到传统的最小二乘估计中，通过选权迭代的方式构造出抗差最小二乘估计。抗差估计的最大优点是能识别异常观测值，利用等价权函数自适应地调节各传感器观测值的比重，有效降低粗差观测值对估计结果的影响[19]。当车轮发生空转/滑行以及卫星信号受遮挡时，ODO和BDS的里程测量误差具有粗差特性。因此，本文基于抗差估计法融合BDS和ODO的观测信息，利用等价权函数降低粗差观测值的权重，减少其对融合结果的影响，以提高列车定位的精确性和可靠性。

设第周期各传感器观测向量为,k(=odo, bds)，列车从−1到时刻的状态向量为，则状态方程和观测方程分别为：

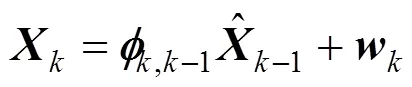
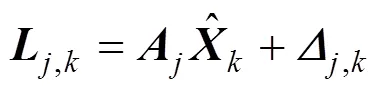
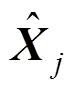
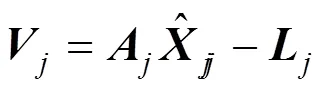
式中：为的残差向量。

为抑制各分量粗差的影响，引入以下抗差极值条件[20]：

式中：为的先验权矩阵；假设各分量不相关，则()为的第个对角线元素；为严凸非减函数；(V)为V的第个分量。

由此可得各传感器的抗差估计解为：

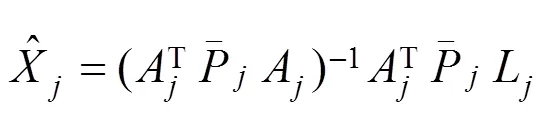
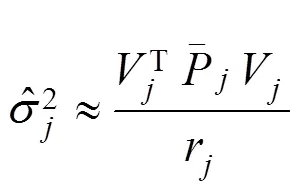
式中：r为L的冗余观测数。令

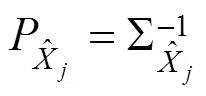
则BDS/ODO抗差融合解为：

式中：

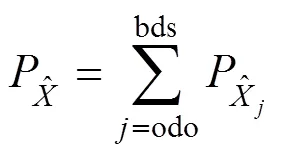
3 仿真与分析

为验证本文提出的基于抗差估计的BDS/ODO组合列车定位方法的性能，在实验室自研的VOBC平台上进行仿真测试。该平台由车载ATP、车载ATO、北斗卫星接收机、里程计、车辆动力学模型仿真软件、ATR(Automatic Train Regulation)仿真软件、区域控制器仿真软件和人机交互界面等组成。平台结构如图1所示。

卫星数据采样周期为1 s，ODO数据采样周期为100 ms。为模拟空转/滑行对ODO里程观测值的影响以及可视卫星较少时对BDS定位结果的影响，给ODO测量里程和BDS位置导出里程加入随机粗差。采用以下3种方案分别进行仿真，方案1：BDS/ ODO常规Kalman滤波融合估计；方案2：BDS/ODO扩展Kalman滤波融合估计；方案3：基于BDS和ODO观测信息抗差解的融合估计。以高精度的BDS载波相位差分解作为里程参考真值，对各方案的估计结果进行分析和评价。

图2为ODO的里程观测误差；图3为BDS位置导出里程的误差；图4为方案1的里程估计误差；图5为方案2的里程估计误差；图6为方案3的里程估计误差。

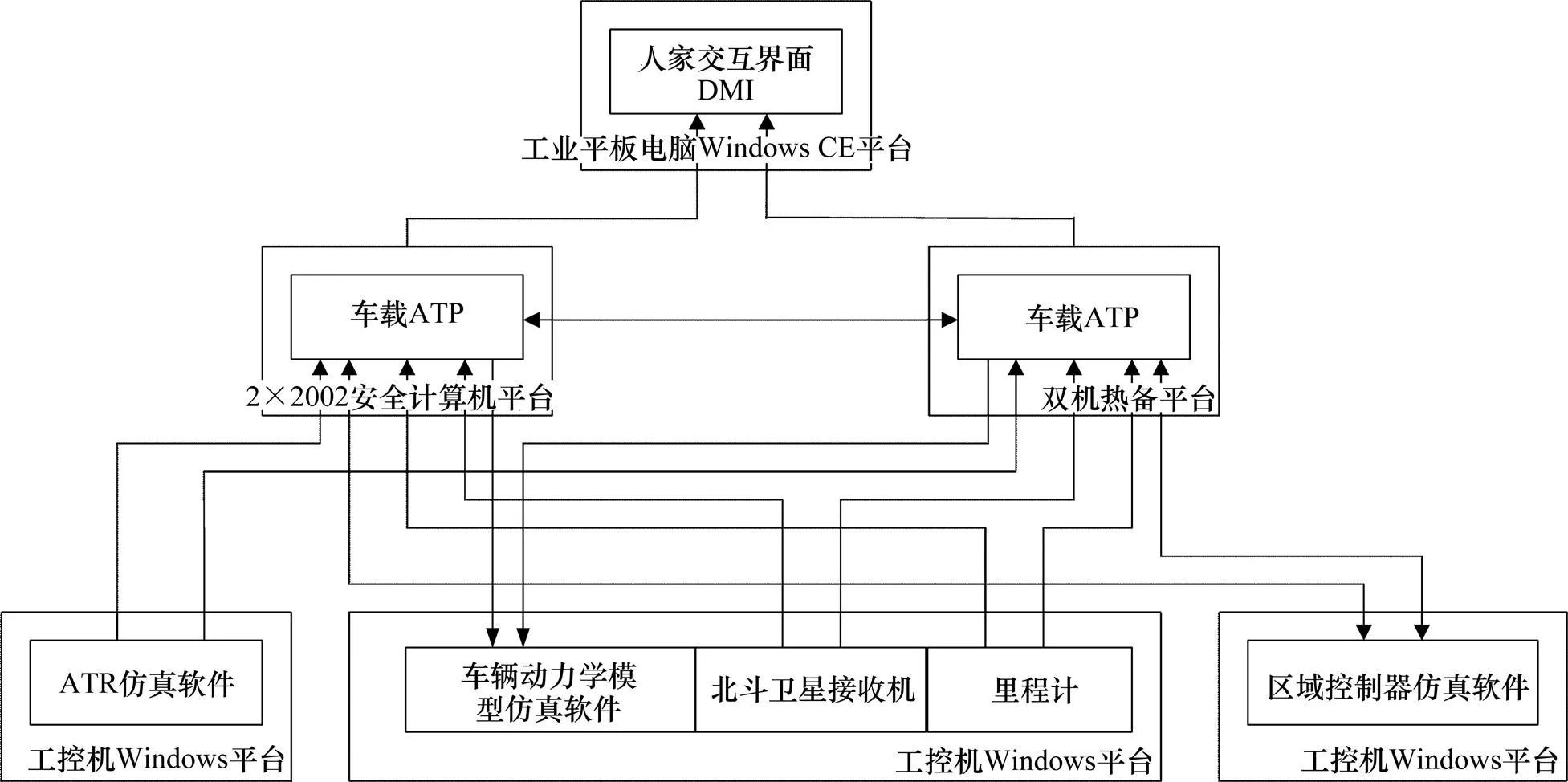
图1 VOBC仿真测试平台

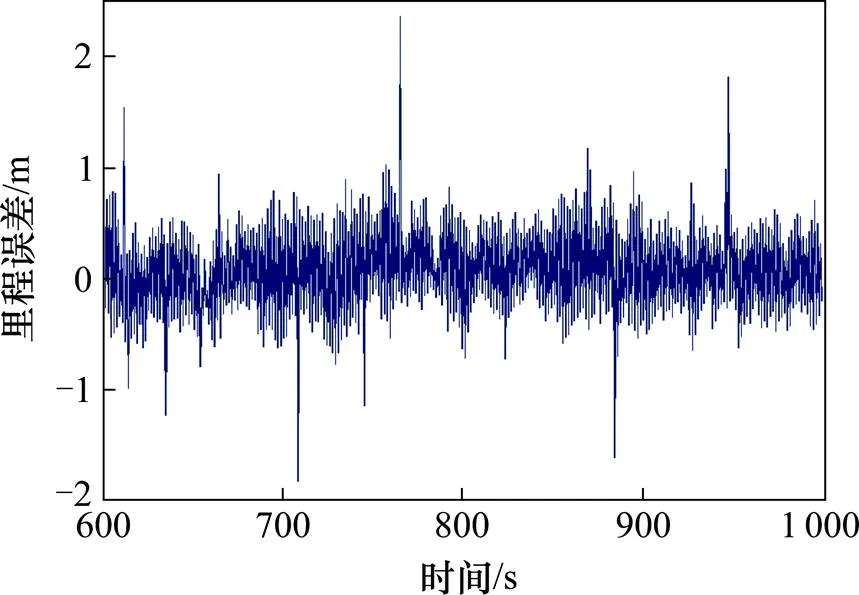
图2 ODO里程观测误差

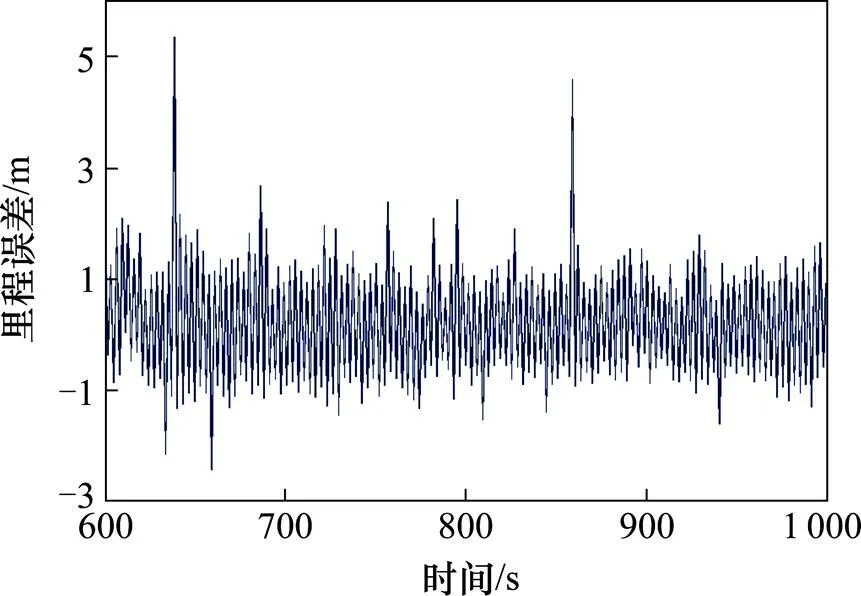
图3 BDS里程观测误差

各方案里程误差的均值(AVE)和均方根(RMS)统计结果如表1所示。

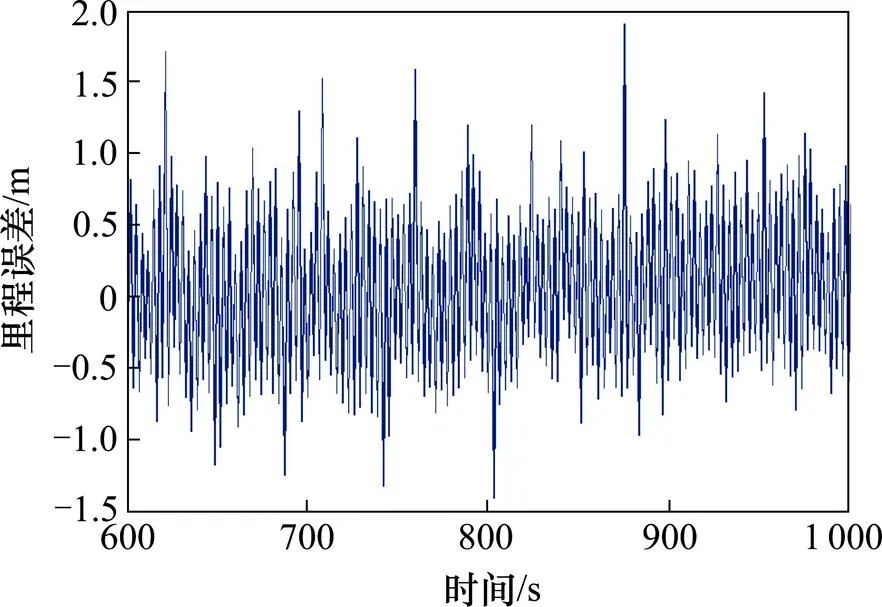
图4 方案1里程估计误差

图5 方案2里程估计误差

由图2可见，ODO单独定位时，空转、滑行造成的粗差较大，依靠ODO自身无法有效克服，里程误差范围为−1.82~2.36 m；由图3可见，采用BDS定位结果解算的里程值，除了可视卫星较少的历元误差较大外，其他历元的里程误差基本控制在2 m以内，误差范围为−2.44~5.37 m；从图4可以看出，BDS/ODO常规Kalman滤波的里程估计误差比2种传感器单独定位有所减小，但效果不明显，误差范围为−1.41~1.89 m；从图5可见，BDS/ODO扩展Kalman滤波的里程估计误差为−0.92~0.94 m；从图6可以看出，BDS/ODO抗差估计融合算法的里程估计误差总体上均较小，误差范围为−0.36~0.37 m。方案3与方案1、方案2相比，里程估计误差分别降低了78%和61%。

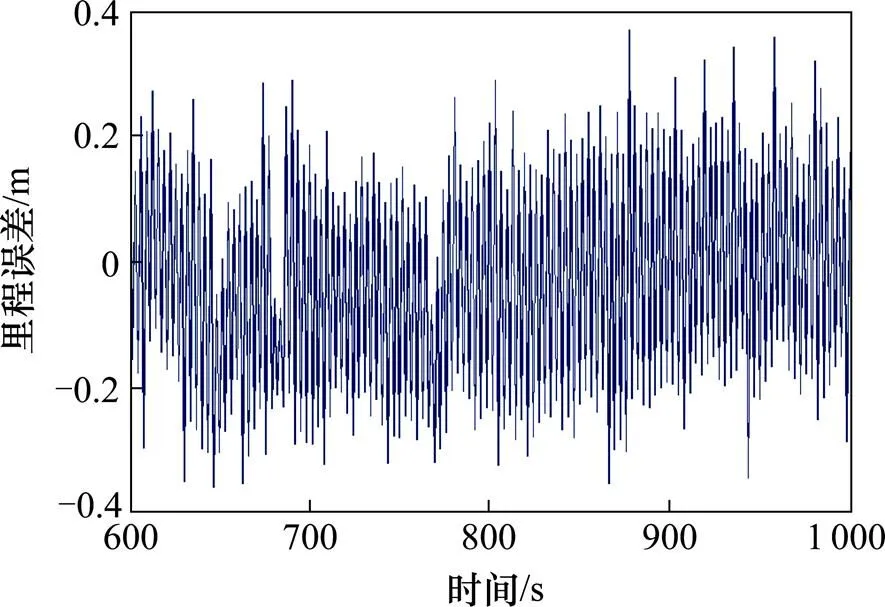
图6 方案3里程估计误差

表1 里程误差统计值

由表1可见，方案1和方案2里程估计误差的RMS和AVE均小于ODO和BDS单独定位的统计结果，但改善效果不明显。而方案3里程估计误差的RMS和AVE分别为0.18和0.12，明显小于方案1和方案2，对误差的抑制效果显著。

同时，为对比各方案融合算法的滤波效率，对仿真时间内各方案的滤波周期进行了统计，方案1，方案2和方案3的滤波周期均值分别为1.033， 1.054和1.012 s。可以看出，本文算法的滤波计算效率优于方案1和方案2，保证了列车组合定位融合估计的实时性。

4 结论

1) 采用BDS和ODO构建列车组合定位系统，既充分利用了目前主流的列车定位传感器，又结合了代表列车定位技术发展趋势的卫星导航系统，实现了二者的优势互补。在简化列车定位系统传感器配置、降低系统成本、提高系统自主性基础上，保证了列车定位的连续性和可用性。

2) 常规Kalman滤波和扩展Kalman滤波均不能有效抑制传感器粗差观测值对融合结果的影响。而抗差估计融合算法通过等价权函数自适应地调节各传感器观测值的比重，能够有效降低粗差观测值对融合结果的影响，具有较强的鲁棒性，同时该算法实现简单，避免了使用传统滤波时参数设置的复杂性，滤波效率高，实时性好。

3) 仿真测试结果表明，在传感器观测值含有粗差的情况下，抗差融合解明显优于常规Kalman滤波解和扩展Kalman滤波解，里程估计误差显著减小，保证了列车定位的精确性和可靠性。

[1] 刘江, 蔡伯根, 王剑, 等. 基于灰色理论的列车组合定位轮径校准方法研究[J]. 铁道学报, 2011, 33(5): 54−59. LIU Jiang, CAI Baigen, WANG Jian, et al. Study on wheel diameter calibration method in integrated train positioning based on gray theory[J]. Journal of the China Railway Society, 2011, 33(5): 54−59.

[2] 乔超, 唐慧佳. 列车里程计定位方法的研究[J]. 兰州铁道学院学报(自然科学版), 2003, 22(3): 116−119. QIAO Chao,TANG Huijia. The method of positioning trains by odometers[J]. Journal of Lanzhou Railway University (Natural Sciences), 2003, 22(3): 116−119.

[3] 蔡伯根. 低成本列控系统的列车组合定位理论与方法[D]. 北京: 北京交通大学, 2010. CAI Baigen. Train integrated positioning methods for low-cost train control system[D]. Beijing: Beijing Jiaotong University, 2010.

[4] 陶汉卿. 基于轮轴和雷达传感器的列车测速测距系统设计与仿真[J]. 城市轨道交通研究, 2017(5): 63−68. TAO Hanqing. Design and simulation of train speed and distance measurement system based on tachometer and doppler radar[J]. Urban Mass Transit, 2017(5): 63−68.

[5] 杨波, 秦永元, 柴艳. 基于简易IMU的低成本列车定位系统研究[J]. 铁道学报, 2006, 28(6): 73−78. YANG Bo, QIN Yongyuan, CHAI Yan. Study of the low cost train positioning system based on simplified IMU[J]. Journal of the China Railway Society, 2006, 28(6): 73−78.

[6] 王剑, 张辉, 蔡伯根, 等. 虚拟应答器研究进展与发展展望[J]. 铁道学报, 2008, 30(2): 71−77. WANG Jian, ZHANG Hui, CAI Baigen, et al. The research progress and prospect of virtural balise[J]. Journal of the China Railway Society, 2008, 30(2): 71−77.

[7] 刘江, 蔡伯根, 唐涛, 等. 基于GPS与惯性测量单元的列车组合定位系统[J]. 中国铁道科学, 2010, 31(1): 123−129. LIU Jiang, CAI Baigen, TANG Tao, et al. Train integrated positioning system based on GPS and inertial measurement unit[J]. China Railway Science, 2010, 31(1): 123−129.

[8] 高社生, 桑春萌, 李伟. 改进的粒子滤波在列车组合定位系统中的应用[J]. 中国惯性技术学报, 2009, 17(6): 701−705. GAO Shesheng, SANG Chunmeng, LI Wei. Application of improved particle filter to integrated train positioning system[J]. Journal of Chinese Inertial Technology, 2009, 17(6): 701−705.

[9] Toledo-Moreo R, Zamora-lzquierdo M A, Ubeda-Miarro B, et al. High integrity IMM-EKF-based road vehicle navigation with low-cost GPS/SBAS/INS[J]. IEEE Transactions on Intelligent Transportation Systems, 2007, 8(3): 491−511.

[10] JIANG Zhuqing, LIU Chonghua, ZHANG Gong, et al. GPS/INS integrated navigation based on UKF and simulated annealing optimized SVM[C]// Vehicular Technology Conference (VTC Fall). 2013: 30−38.

[11] Arasaratnam I, Haykin S. Cubature kalman filters[J]. IEEE Transactions on Automatic Control, 2009, 54(6): 1254−1269.

[12] Schlingelhof M, Betaille D, Bonnifait P, et al. Advanced positioning technologies for co-operative systems[J]. IET Intelligent Transport Systems, 2008, 2(2): 81−91.

[13] Hegarty C, Chatre E. Evolution of the global navigation satellite system (GNSS)[J]. Proceedings of the IEEE, 2008, 96(12): 1902−1917.

[14] 刘江, 蔡伯根, 王剑. 基于卫星导航系统的列车定位技术现状与发展[J]. 中南大学学报(自然科学版), 2014, 45(11): 4033−4042. LIU Jiang, CAI Baigen, WANG Jian. Status and development of satellite navigation system based train positioning technology[J]. Journal of Central South University (Science and Technology), 2014, 45(11): 4033−4042.

[15] Georgy J, Korenberg M J. Modeling the stochastic drift of a MEMS-based gyroscope in Gyro/Odometer/GPS integrated navigation[J]. IEEE Transactions on Intelligent Transportation Systems, 2010, 11(4): 856−872.

[16] 李卫东, 侯丽虹, 王友生. 基于BDS/GSM-R组合列车定位方法的研究[J]. 铁道科学与工程学报, 2016, 13(3): 552−556. LI Weidong, HOU Lihong, WANG Yousheng. Study of train positioning method based on BDS/GSM-R combination[J]. Journal of Railway Science and Engineering, 2016, 13(3): 552−556.

[17] 李克昭, 韩梦泽, 孟福军. 北斗系统的特色、机遇与挑战[J]. 导航定位学报, 2014, 2(2): 21−25. LI Kezhao, HAN Mengze, MENG Fujun. Features,opportunities and challenges of BDS[J]. Journal of Navigation and Positioning, 2014, 2(2): 21−25.

[18] 李鹤峰, 党亚民, 秘金钟, 等. 北斗卫星导航系统的发展、优势及建议[J]. 导航定位学报, 2013, 1(2): 49−54. LI Hefeng, DANG Yamin, BEI Jinzhong, et al. Development、advantages and suggestions of Beidou navigation satellite system[J]. Journal of Navigation and Positioning, 2013, 1(2): 49−54.

[19] 杨元喜. 抗差估计理论及其应用[M]. 北京: 八一出版社, 1993. YANG Yuanxi. Robust estimation and its applications[M]. Beijing: Bayi Press, 1993.

[20] 杨元喜, 高为广. 基于多传感器观测信息抗差估计的自适应融合导航[J]. 武汉大学学报(信息科学版), 2004, 29(10): 885−888.YANG Yuanxi, GAO Weiguang. Integrated navigation based on robust estimation outputs of multi-sensor measurements and adaptive weights of dynamic model information[J]. Geomatics and Information Science of Wuhan University, 2004, 29(10): 885−888.

[21] YANG Y, XU T. An adaptive Kalman filter based on sage windowing weights and variance components[J]. Journal of Navigation, 2003, 56(2): 231−240.

(编辑 蒋学东)

BDS/ODO integrated train positioning method based on robust estimation

CAI Xuan1, WAN Changlin2

(1. State Key Laboratory of Traction Power, Southwest Jiaotong University, Chengdu 610031, China; 2. School of Information Science and Technology, Southwest Jiaotong University, Chengdu 610031, China)

According to the actual needs of the train positioning, beidou navigation satellite system together with the odometer are used to build the train combination positioning system, which takes the advantages of the two to be complementary. Aiming at the problem of using conventional Kalman filter for the train combination positioning fusion estimation, a train combination positioning method based on robust estimation is proposed. On one hand, the fusion calculation is carried out by applying the robust estimation to the sensor observation information. On the other hand, the equivalent weight function is used to adaptively adjust the proportion of each sensor’s observed value. Therefore, the effects of gross observations on fusion results will be effectively reduced. The simulation results show that, in the case where the sensor observations contain gross errors，the combination positioning solution based on the robust estimation is superior to both the conventional Kalman filter solution and the extended Kalman filter solution. The robust estimation method can enhance the robustness of the system, improve the filter real-time and ensure the accuracy and reliability of the train positioning.

train positioning; integrated positioning; beidou navigation satellite system; odometer; robust estimation; equivalent weight function

10.19713/j.cnki.43−1423/u.2018.10.027

U284

A

1672 − 7029(2018)10 − 2654 − 07

2017−08−31

国家自然科学基金资助项目(60776832)

蔡煊(1982−)，男，四川德阳人，博士研究生，从事交通信息工程及控制，智能交通方向的研究；E−mail：390474685@qq.com