衡山湘江大桥换索工程研究

谢福君，张家生



衡山湘江大桥换索工程研究

谢福君1,2，张家生1

(1. 中南大学 土木工程学院，湖南 长沙 410075； 2. 衡阳市交通运输局 湖南 衡阳 421001)

结合衡山湘江大桥斜拉索换索工程并基于最优化原理，介绍索力的优化理论，研究该桥的换索原则、方案及其施工工艺。研究结果表明：在换索工作中，主梁的弯矩、轴力，索塔根部弯矩、轴力均呈现周期性变化。拆除旧索，引起其它拉索产生内力重分布，索力变化明显。拆除某号拉索，影响最大的是与之相邻的2根索，索力均增大，其次影响最大是索塔背面相近拉索，索力均减小。而其他有关拉索在被更换时，该索的索力所受到的影响相对较小。拆除旧索，主梁线形及塔顶位移发生变化，近似呈现周期变化。根据最优化原理，调索最终(实测)索力与理论索力基本一致，最大误差约1%。

最优化；斜拉桥；换索；过程

斜拉桥具有超大的跨度，近年来在我国的应用日渐增加。这种桥梁在长期使用过程当中，一些问题也开始暴露出来，例如斜拉索极易损坏，保养的难度较大，尤其是换索工程，不仅对施工工艺有着严格要求，而且换索方案和原则还没有统一，换索质量和施工模式还没有确定，这些都需要在换索时进行重点关注[1]。李宏江[1]对当前的拉索检测与评定技术现状进行了分析与评价，指出新桥的设计应当对运营期换索问题予以充分的考虑，同时应着力开发不中断交通条件下的换索技术。成永强[2]通过对国内外既有斜拉桥换索实例的调研，总结了既有斜拉桥换索的经验，提出了现有换索技术的不足，并给出了建议。孙全胜等[3]运用神经网络理论，结合一座双塔三跨混凝土斜拉桥换索施工过程，对斜拉桥换索过程索力和主梁标高进行预测研究。孙全胜等[4]通过建模计算分析，将参数增量变化分析方法运用于皎平渡斜拉桥换索工程实践。兰建雄[5]介绍了上海恒丰北路斜拉桥换索的施工工艺、拉索安装索力计算、施工支架和换索期间的交通组织措施。田波等[6]介绍了重庆市涪陵长江大桥换索涉及的相关设计内容及其技术特点。唐继舜等[7]结合岷江大桥换索工程，详述了斜拉桥索力监控测量、换索方法及施工过程监控。朱战良[8]介绍了广东九江大桥(斜拉桥)的拉索病害调查、新索设计、换索施工工艺、调索方案比选及计算、调索工艺等。张 恒[9]介绍了一种基于切割换张法的快速更换拉索技术。孙全胜等[10]结合皎平渡斜拉桥换索工程，运用卡尔曼滤波法对斜拉桥换索进行施工控制。施洲等[11]通过键为崛江大桥换索工程前后的两次检测与荷载试验，表明换索前索力异常，换索前的检测验证了斜拉索存在严重的病害，两次固有频率的测试结果表明斜拉索病害会明显导致结构固有频率值降低。李劭晖等[12]结合西樵大桥换索工程，探讨了斜拉桥换索过程中的施工监控技术。本文以衡山湘江大桥为工程背景，对该桥的换索方案进行了全面分析，重点研究其换索工艺、方法和施工及其工艺的管控等方面，通过对此换索工程的研究，从而为同类斜拉桥的日后维护提供一定的参考。

1 索力优化原理

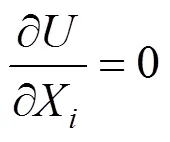
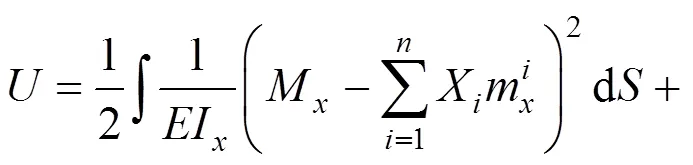
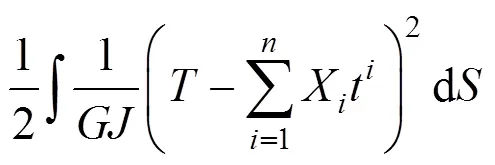
式中：M为结构方向弯矩；M为结构方向弯矩；为结构的扭矩。

结合主梁线形约束目标函数，即至少有N个关键点的标高接近或等于指定的标高，见式(2)。

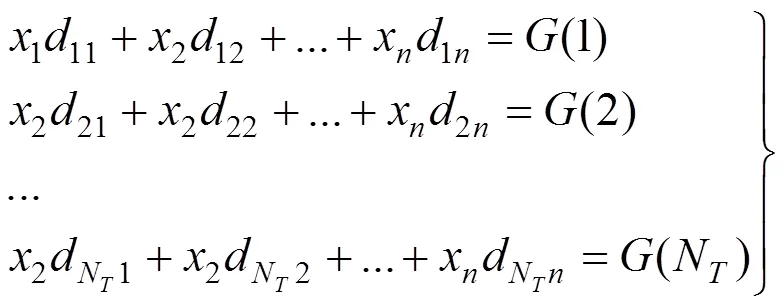
式中：d为由x=1引起序号为的节点竖向位移。

采用惩罚参数法，构造一个惩罚函数P,见式(3)。引入惩罚函数，构造新的泛函，见式(4)。

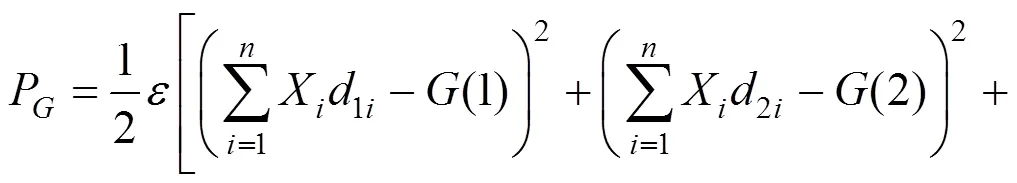
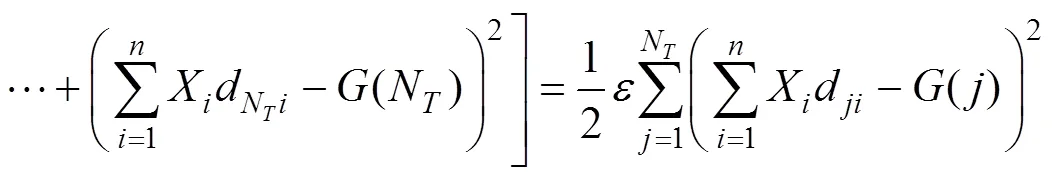
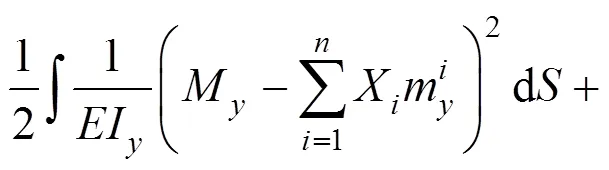
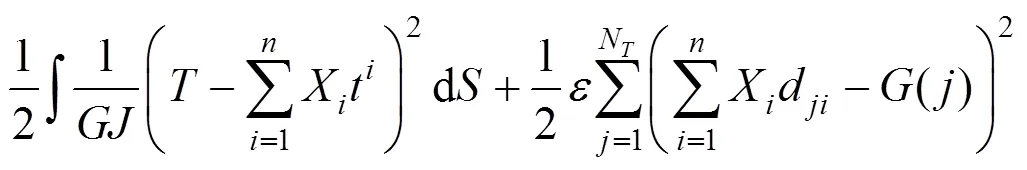
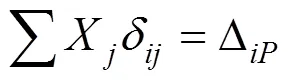
求解式(5)，X极为所求的斜拉索索力增量。

2 工程概况及换索方案与原则

衡山湘江大桥位于S314省道K19+452 m处，主桥为三塔单索面平行索预应力混凝土斜拉桥(3×45 m＋2×90 m＋2×45 m)，采用单箱单室箱型截面。其中一塔对应的拉索为12条，共6对，具体布置见图1。

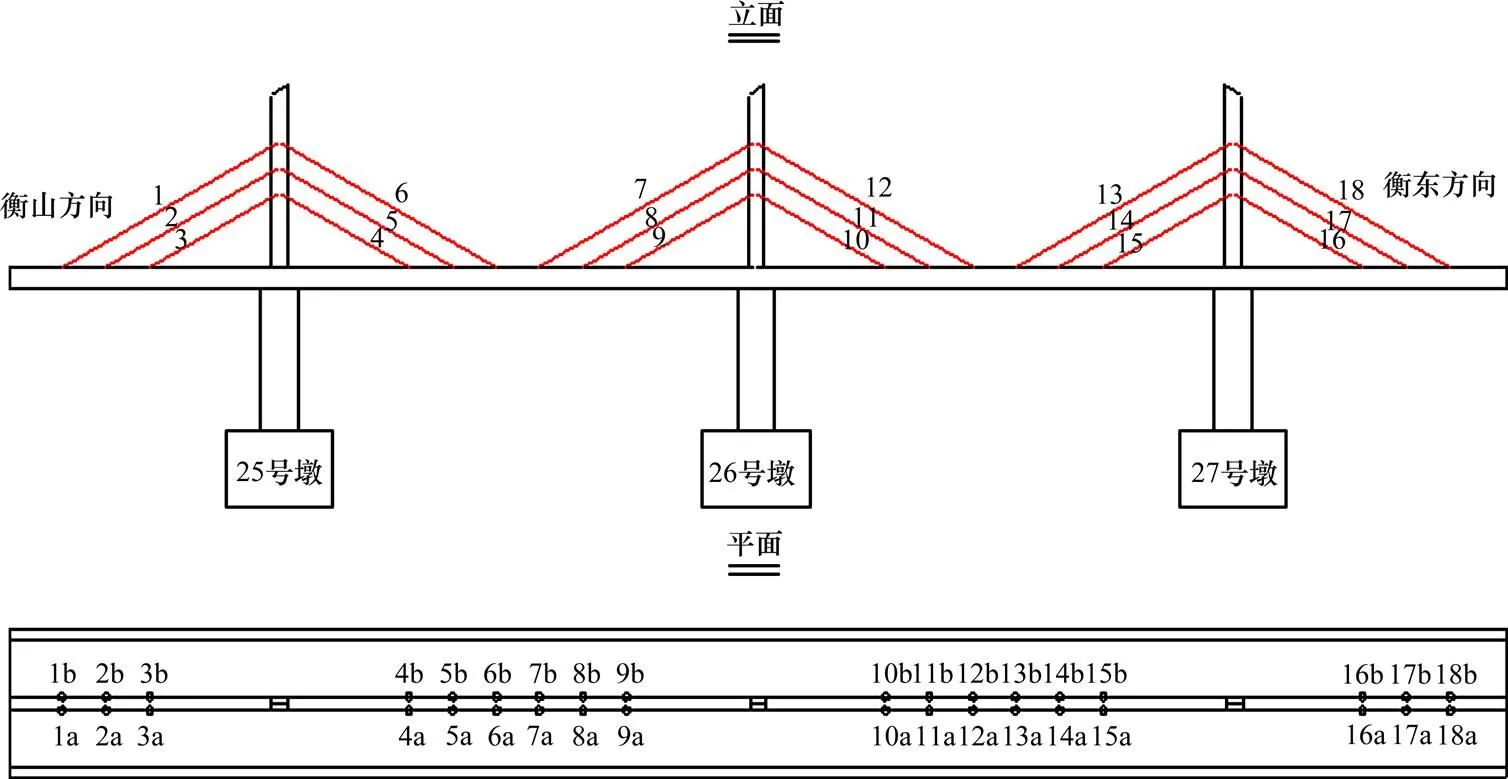
图1 桥梁编号化处理

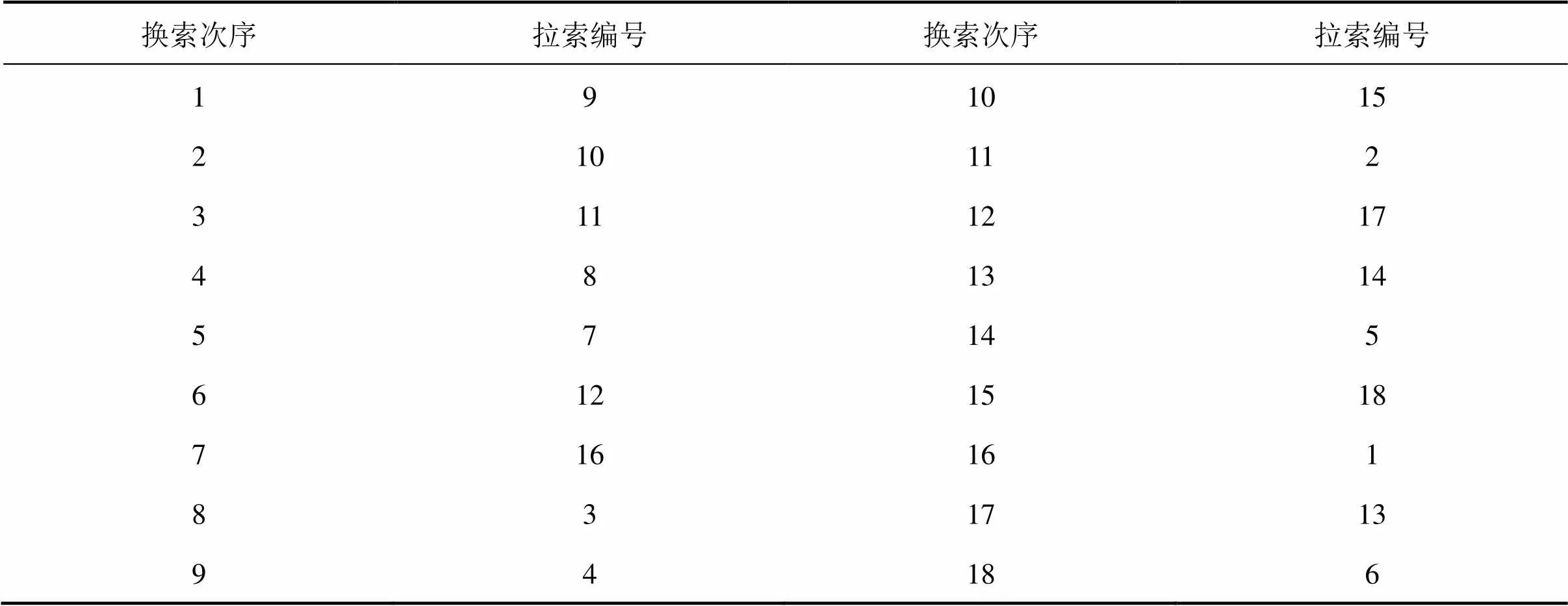
表1 衡山湘江大桥斜拉索的更换顺序表

在施工时，其主梁内应力以及相关的拉索作用力都会出现显著改变，为了让这种变化效应变得更小，可以按照下面的原则来更换：

①先在中塔处更换，然后再进行边塔更换，即按照26号塔、25号塔、27号塔的顺序进行更换(考虑结构的对称性及施工因素，同时确使换索施工对结构的影响最小)；②优先更换短索，然后再进行长索更换；③施工工艺为反对称，也就是按照上下游进行错落式反对称方法更换；④每次仅更换1根索；⑤当1对拉索被更换成功之后，还需要对它们的作用力进行分析，直到作用力符合要求，才能进行下1对的更换；⑥更换拉索时，当天必须要完成1根；⑦如果拉索的安全系数值已经很小，此时需要对其进行优先式更换。

衡山湘江大桥斜拉索的更换顺序见表1。

3 衡山湘江大桥换索工程施工过程分析

首先结合施工设计，使用MIDAS分析系统，对该大桥的换索工程进行仿真模拟分析。

该桥有限元模型共计376个节点，390个单元，采用变截面梁单元模拟主梁和索塔，采用只受拉桁架单元模拟斜拉索。为了将整个模拟过程进行简化，可以预设换索之后的索力和设计要求的索力一致，即任一根拉索更换完成之后对全桥结构不产生影响。

结合此桥的换索工程，当旧拉索被撤出时，就是对应的时间点，各个旧索拆除施工过程，主梁关键截面(例如边跨跨中、主梁索塔支点截面、中跨跨中截面)等相关的应力改变，可以参见图2~3。

(a) 边跨跨中；(b) 中跨跨中；(c) 主梁25号塔支点；(d) 主梁26号塔支点

图2中，在换索工作中，主梁弯矩的变化具有显著周期性。另外，在对1号索对进行拆除时，中跨、边跨的跨中截面受到显著影响，另外25号的索塔支点截面弯矩也受到最大影响。分别达到−5 190.86 kN∙m，7 157.07 kN∙m及−12 576.94 kN∙m；拆除9号旧索对主梁26号索塔支点截面弯矩影响最大，达到−17 145.85 kN∙m。

同理，由图3可得，拆除旧索，引起主梁轴力呈现周期性变化。经过计算可知，在拆除时，中跨的跨中截面轴力受到的影响最低。而2号旧索对被拆除时，其跨中截面轴力将会受到最大影响，其值为1 649.46 kN；拆除3号旧索对主梁25号索塔支点截面轴力影响最大，达到1 435.58 kN；拆除9号旧索对主梁26号索塔支点截面轴力影响最大，达到2 119.73 kN。

衡山湘江大桥各个旧索拆除施工过程，索塔根部截面内力见图4~5。

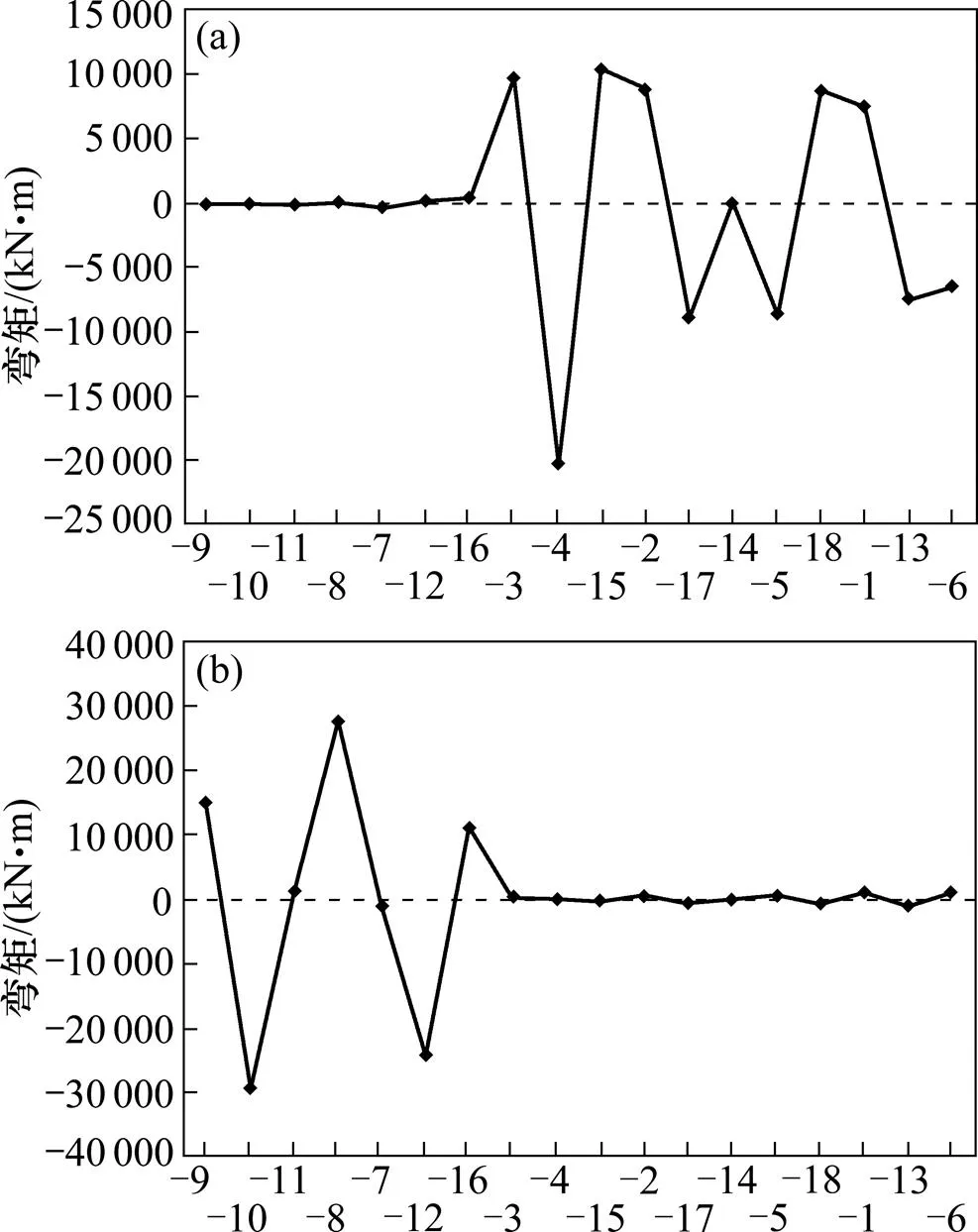
(a) 25号索塔根部；(b) 26号索塔根部

由图4~5可以看出，拆除旧索，引起索塔根部弯矩、轴力呈现周期性变化。计算表明，拆除4号旧索对25号索塔根部截面弯矩影响最大，达到−20 301.0 kN∙m；拆除10号旧索对26号索塔根部截面弯矩影响最大，达到−29 506.33 kN∙m；拆除13号旧索对25号索塔根部截面轴力影响最大，达到−1 271 kN；拆除16号旧索对26号索塔根部截面轴力影响最大，达到−2 070.71 kN。

(a) 25号索塔根部；(b) 26号索塔根部

根据衡山湘江大桥换索工程的施工顺序，以各旧索拆除为时间节点，各个旧索拆除施工过程，拉索索力变化见图6。

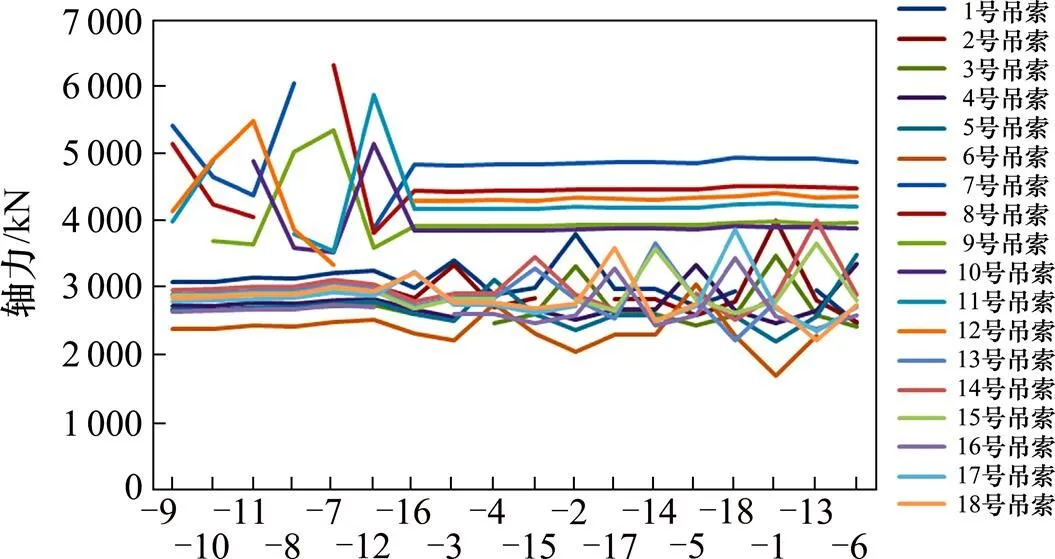
图6 换索时对应的索力分析

由图6可以看出，拆除旧索，引起其他拉索产生内力重分布，索力变化明显，通过计算可知，当进行更换工程时，8号拉索的索力变化最大，即换索之前8号索力为4 404.809 kN，拆除7号索，8号索力为6 309.263 kN，相对变化达到43.23%。换索过程索力的相对变化见图7。

为了具体分析旧拉索拆除过程各个拉索的索力变化，分别选取1，3，4，6，7及9号拉索为研究对象，各索索力变化见图8。

由图8可以看出，拆除某号拉索，影响最大的是与之相邻的两根索，索力均增大，其次影响最大是索塔背面相近拉索，索力均减小。而其他有关拉索在被更换时，该索的索力所受到的影响就相对较小。

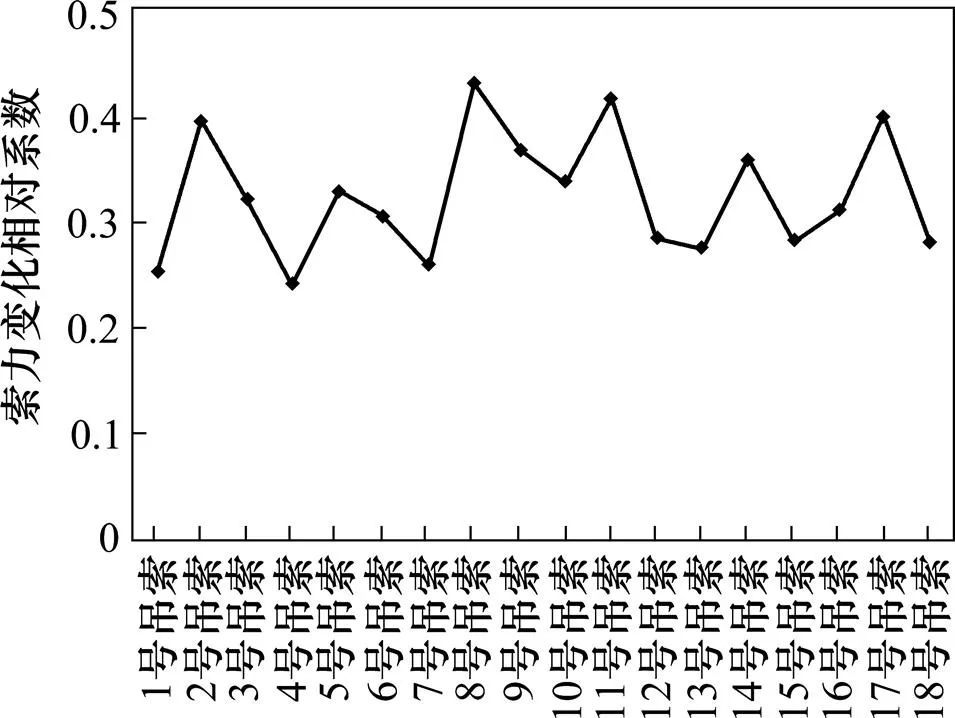
图7 换索过程索力的相对变化

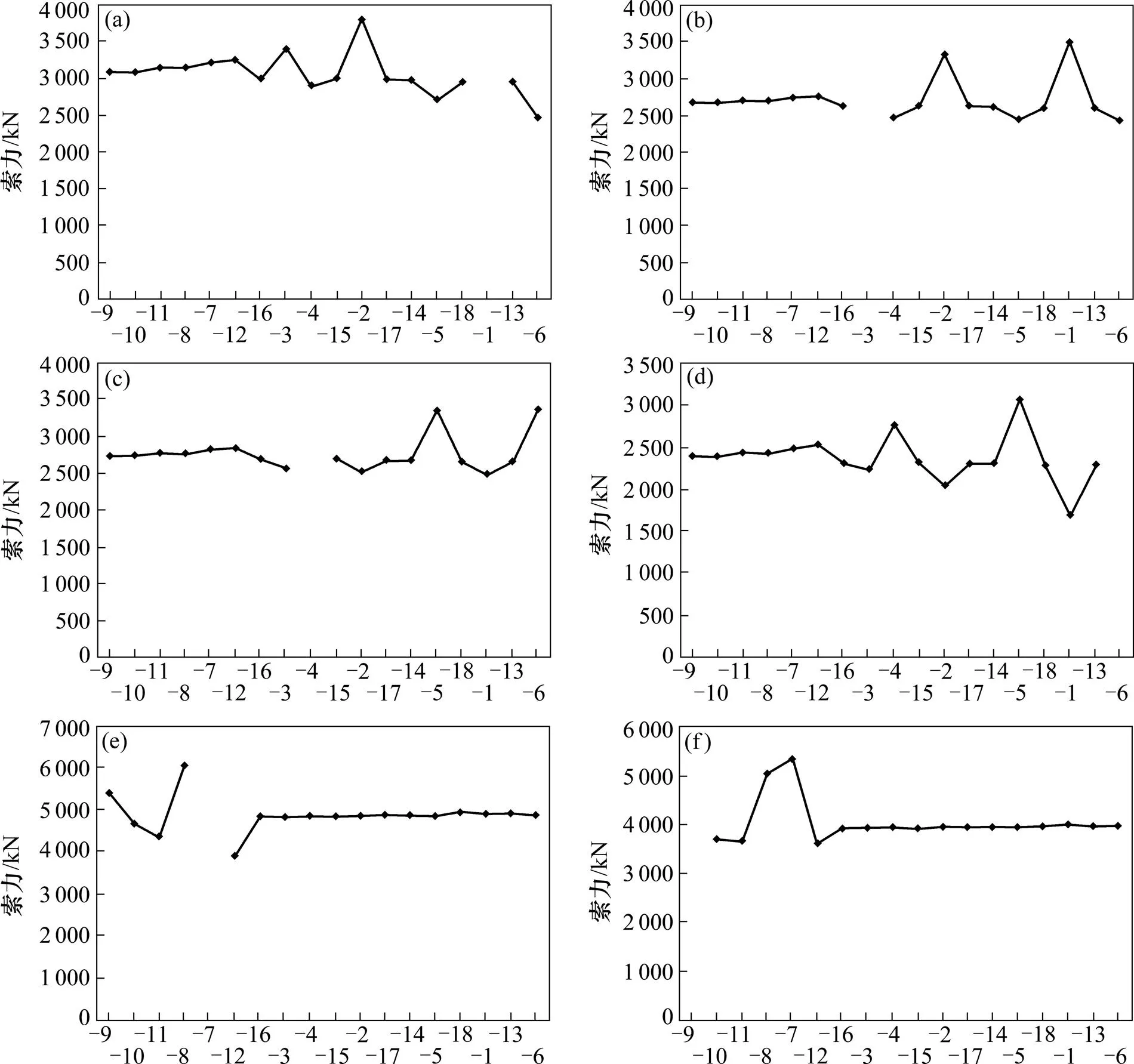
(a) 1号拉索；(b) 3号拉索；(c) 4号拉索；(d) 6号拉索；(e) 7号拉索；(f) 9号拉索

根据衡山湘江大桥换索工程的施工顺序，以各旧索拆除为时间节点，各个旧索拆除施工过程，主梁的边跨、中跨的跨中挠度变化趋势可以参见图9。边塔及中塔塔顶位移变化见图10。

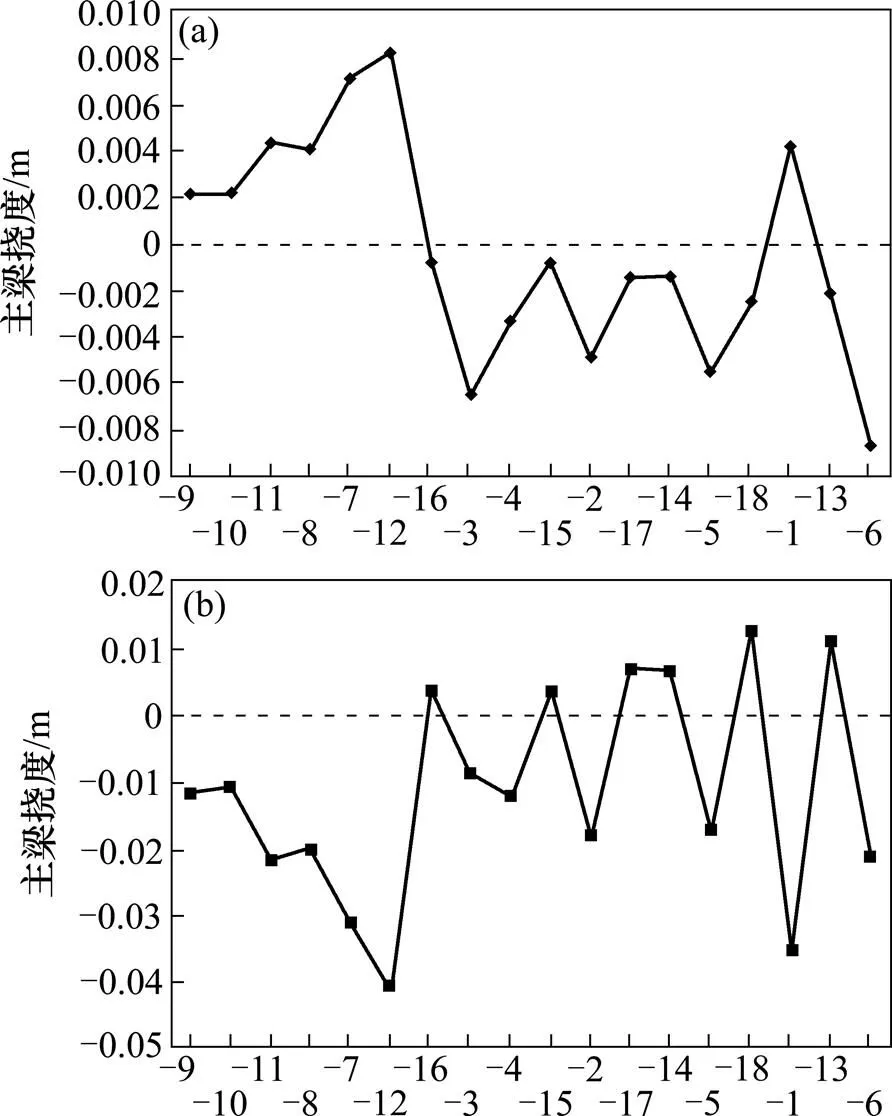
(a) 边跨跨中；(b) 中跨跨中

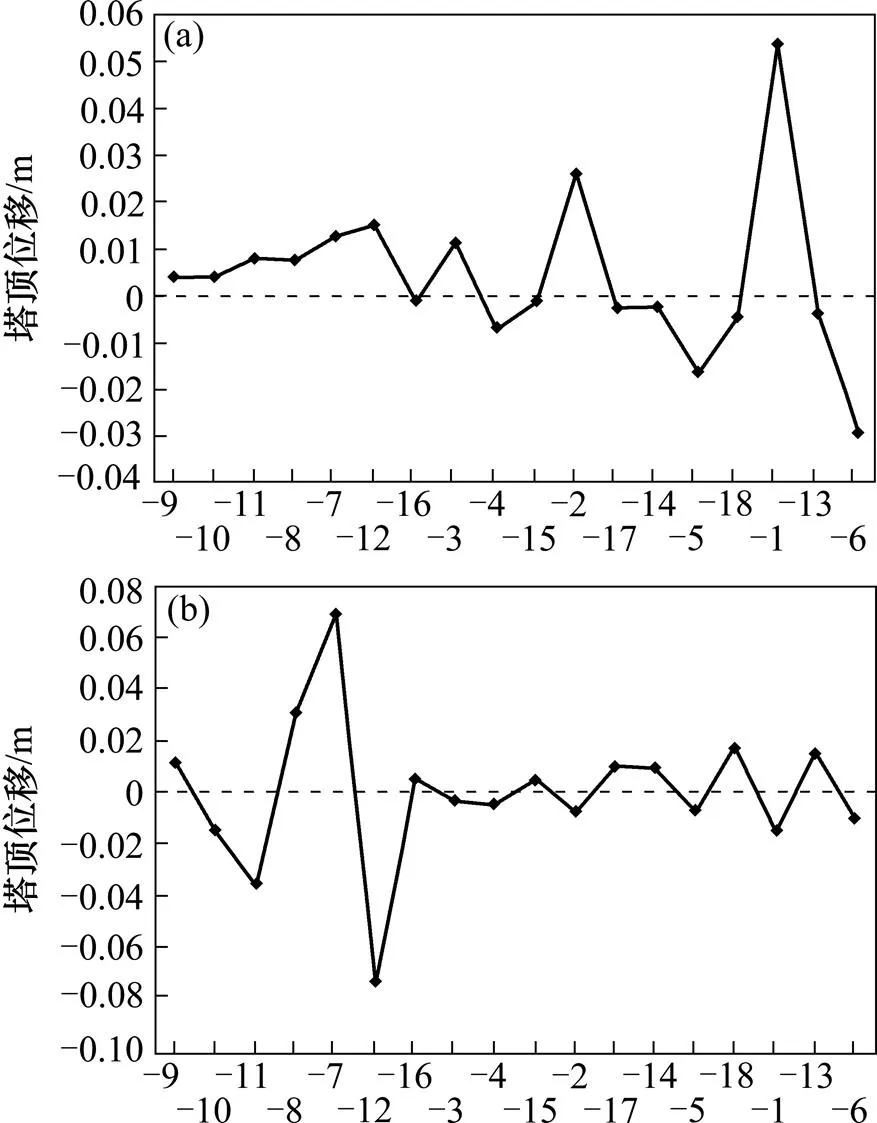
(a) 边塔；(b) 中塔

由图9可得，拆除旧索，引起其它拉索产生内力重分布，主梁线形发生变化，近似呈现周期变化。根据计算结果，主梁关键点—例如边跨跨中、中跨跨中挠度变化幅度较大，最大幅度分别为−8.77 mm和−40.87 mm。

由图10可得，拆除旧索，引起其他拉索产生内力重分布，塔顶位移近似呈现周期变化。根据计算结果，边塔塔顶、中塔塔顶位移变化幅度较大，最大幅度分别为5.39 mm和−7.42 mm。

4 衡山湘江大桥最终索力

根据索力优化原理，选取主梁四分点、跨中挠度及塔顶位移为控制指标，假定结构的现存内力与期望的设计内力相符，罚函数中引入=108，采用MIDAS软件进行结构计算(MIDAS计算模型见图11)，结合期初的实测索力，衡山湘江大桥确定得到的最终索力见表2。具体对比见图12~13。

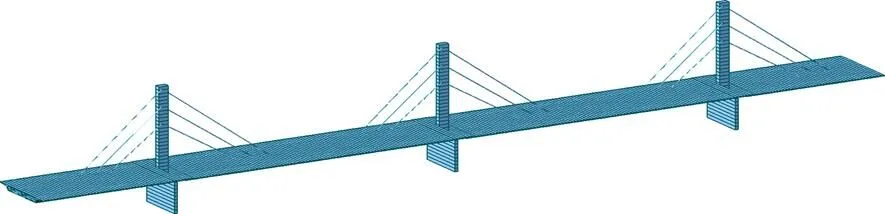
图11 MIDAS计算模型

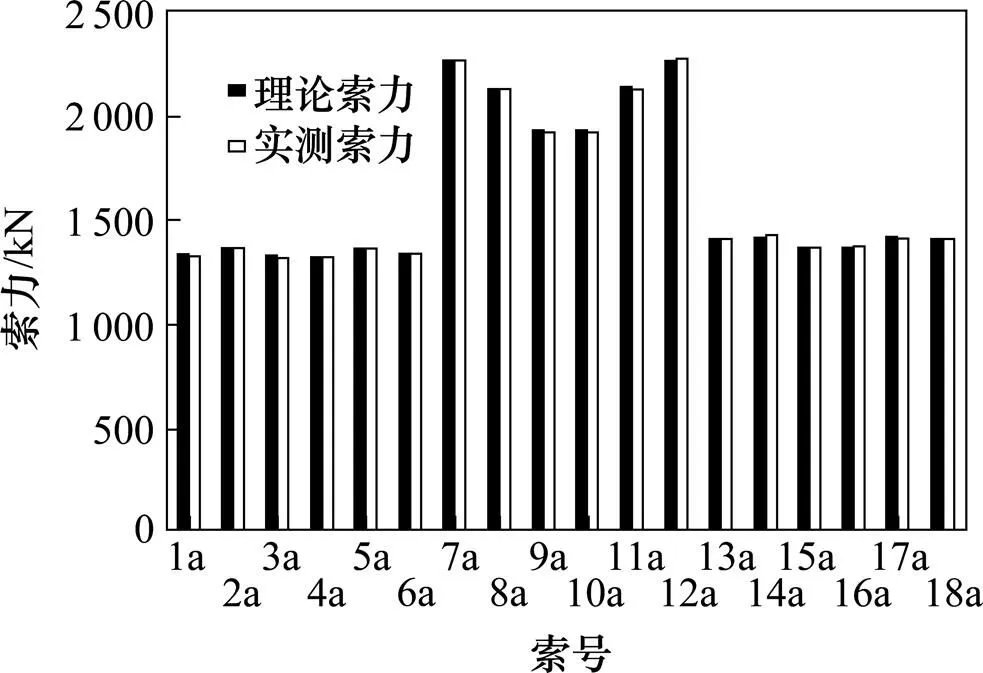
图12 上游侧理论索力与实测索力比较图

由表2、图12~13可以看出，调索最终(实测)索力与理论索力基本一致，最大误差约1%。

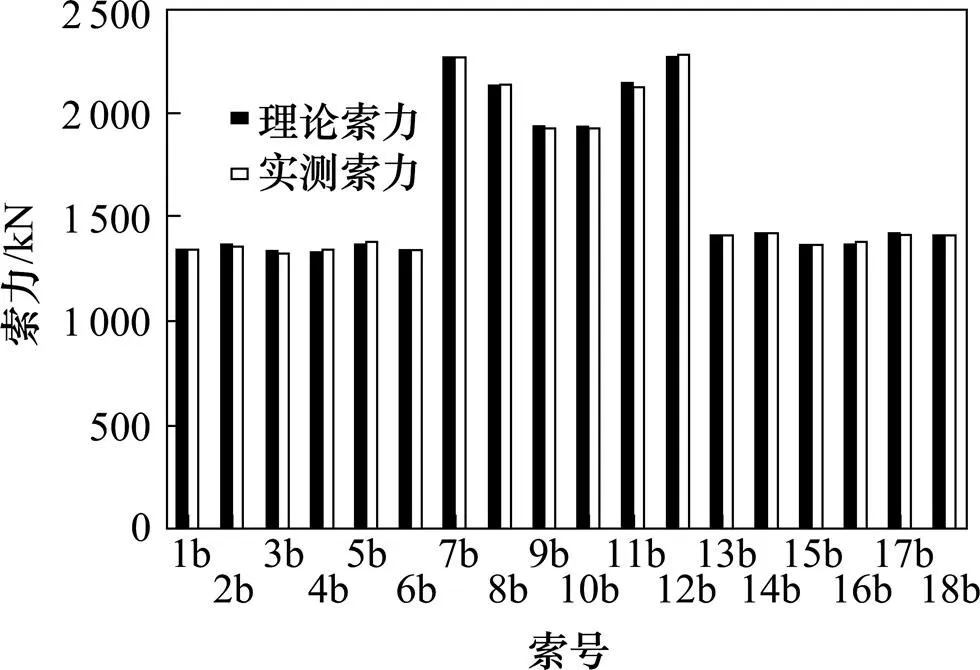
图13 下游侧理论索力与实测索力比较图

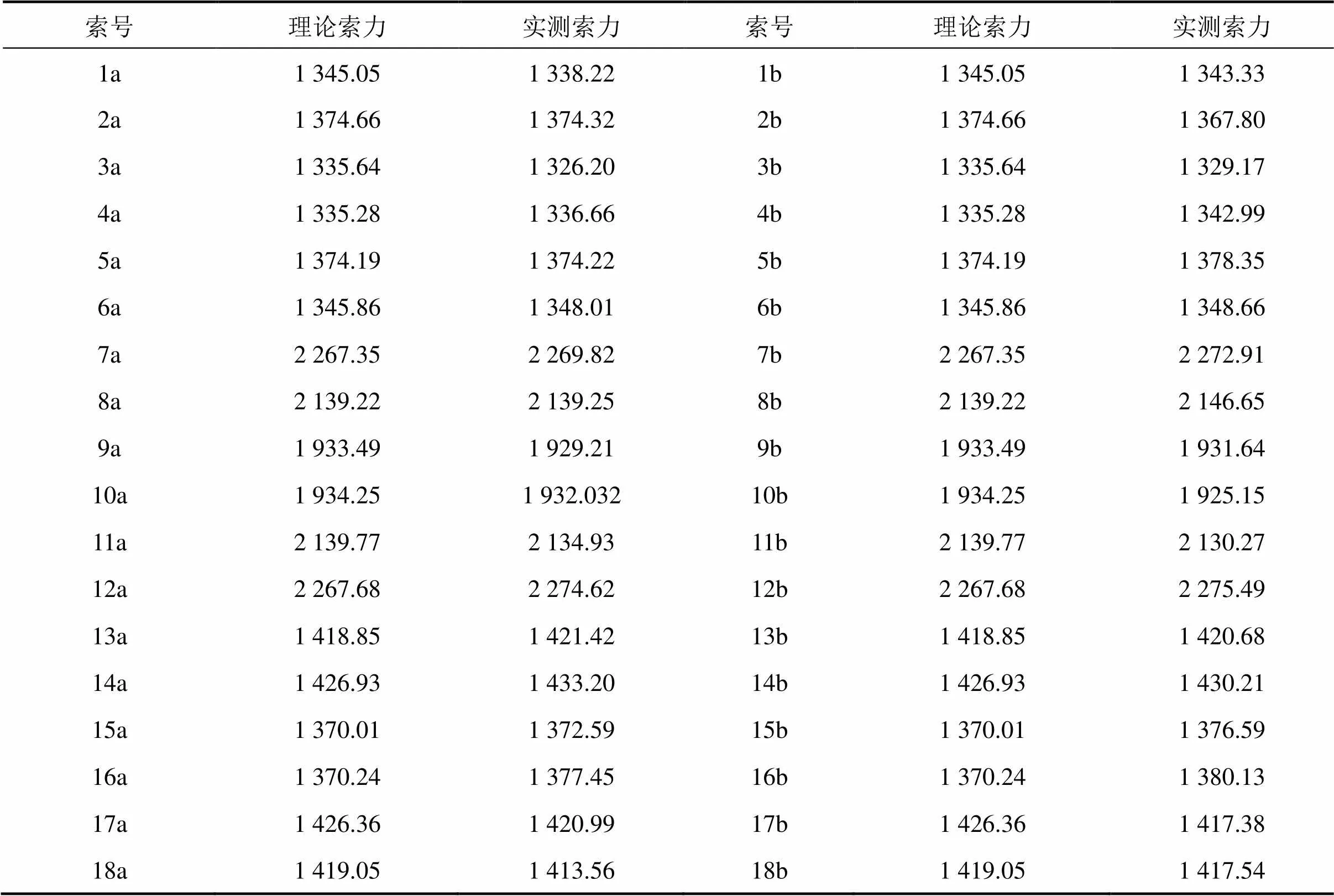
表2 衡山湘江大桥换索工程理论最终索力与实测索力一览表

5 结论

1) 根据拟定的换索方案，在旧索的拆除、更换施工过程中，主梁弯矩、轴力呈现周期性变化；索塔根部弯矩、轴力也呈现周期性变化。

2) 拆除旧索，引起其它拉索产生内力重分布，索力变化明显。计算结果表明，拉索更换过程中，8号拉索的索力变化最大，相对变化达到43.23%。拆除某号拉索，影响最大的是与之相邻的两根索，索力均增大，其次影响最大是索塔背面相近拉索，索力均减小。而其他有关拉索在被更换时，该索的索力所受到的影响相对较小。

3) 拆除旧索，主梁线形及塔顶位移呈现近似周期变化。根据最优化原理，调索最终(实测)索力与理论索力基本一致，最大误差约1%。

[1] 李宏江. PC斜拉桥拉索使用现状及其养护技术进展[J].公路工程, 2014(5): 165−169. LI Hongjiang. The current service status and maintenance advances of stay cables in prestressed concrete cable-stayed bridges[J]. Highway Engineering, 2014(5): 165−169.

[2] 成永强. 既有斜拉桥换索状况综述[J]. 山西建筑, 2015, 36(25): 332−334. CHENG Yongqiang. Overview on cable replacement condition of existing cable-stayed bridge[J]. Shanxi Architecture, 2015, 36(25): 332−334.

[3] 孙全胜, 吴桐. BP神经网络法在斜拉桥换索施工控制中的应用研究[J]. 中国安全科学学报, 2010, 20(7): 21−25. SUN Quansheng, WU Tong. Application of BP neural network in the cable-replacing construction control of cable-stayed bridge[J]. China Safety Science Journal, 2010, 20(7): 21−25.

[4] 孙全胜, 杨建喜. 参数增量变化分析在斜拉桥换索施工控制中的应用[J]. 世界桥梁, 2010(1): 53−55. SUN Quansheng, YANG Jianxi. Application of parameter increment variation analysis to construction control of cable replacement of cable-stayed bridges[J]. World Bridge, 2010(1): 53−55.

[5] 兰建雄. 独塔单索面斜拉桥换索施工[J]. 中国市政工程, 2014, 112(6): 33−36. LAN Jianxiong. Construction of cable exchanging for cable-stayed bridge with one pylon and single cable plane[J]. China Municipal Engineering, 2014, 112(6): 33−36.

[6] 田波, 梁健. 涪陵长江大桥换索设计[J]. 四川建筑, 2016, 36(2): 247−249. TIAN Bo, LIANG Jian. Design of cable replacement in Yangtze River bridge Fuling[J]. Sichuan Architecture, 2016, 36(2): 247−249.

[7] 唐继舜, 代璞. 斜拉桥换索施工监控技术探讨[J]. 桥梁建设, 2005(1): 65−68. TANG Jishun, DAI Pu. Research of construction monitoring techniques for cable-stayed bridge cable replacement[J]. Bridge Construction, 2005(1): 65−68.

[8] 朱战良. 广东九江大桥换索技术[J]. 中外公路, 2003, 23(5): 20−24. ZHU Zhanliang. Guangdong Jiujiang bridge’s cables replacement technology[J]. Journal of China & Foreign Highway, 2003, 23(5): 20−24.

[9] 张恒. 基于切割放张法的快速更换拉索技术研究[J]. 公路交通技术, 2015, 6(5): 60−62. ZHANG Heng. Research on stayed cables quick- replacing technique based on cutting pay-off method[J]. Highway Traffic Technology, 2015, 6(5): 60−62.

[10] 孙全胜, 于海营. 卡尔曼滤波法在斜拉桥换索中的应用[J]. 中外公路, 2009, 29(6): 153−156. SUN Quansheng, YU Haiying. Application of Kalman filtering method in cables replacement in cable-stayed bridges[J]. Journal of China & Foreign Highway, 2009, 29(6): 153−156.

[11] 施洲, 蒲黔辉, 夏招广. 犍为岷江大桥换索前后检测及荷载试验的比较与分析[J]. 公路, 2007, 6(6): 7−11. SHI Zhou, PU Qianhui, XIA Zhaoguang. Comparison and analysis of inspection and loading tests before and after cable replacement of Qianwei Minjiang great bridge[J]. Highway, 2007, 6(6): 7−11.

[12] 李劭晖, 黄林根, 翁思熔. 西樵大桥换索工程施工监控技术研究[J]. 城市道桥与防洪, 2010, 2(2): 92−94. LI Shaohui, HUANG Lingen, WENG Sirong. Research on construction monitoring techniques of cable replacement of Xiqiao bridge[J]. Urban Roads Bridges & Flood Control, 2010, 2(2): 92−94.

[13] Powers T, Price K, He E, et al. Reconstruction of North Avenue Bridge over the Chicago river, Chicago, Illinois[C]// 6th International Bridge Engineering Conference, Boston, 2005: 459−464.

(编辑 涂鹏)

Research on cables replacement for Hengshan Xiangjiang bridge

XIE Fujun1,2, ZHANG Jiasheng1

(1. School of Civil Engineering, Central South University, Changsha 410075, China; 2. Transport Bureau of Hengyang City, Hengyang, 421001, China)

Based on an optimization theory, the optimization theory of cable force is introduced first. Take Hengshan Xiangjiang bridge as an example, the cables’ replacement plan and principle and construction technology are detailed introduced. During the construction period of cables replacement, bending moment and axial force of main girder appear periodic changes as well as bending moment and axial force at the bottom of cable tower. When demolishing one old cable, other cables’ tension has obvious redistribution. Replacement of a cable has the greatest influence on the adjacent two cables, their cable forces increase. It has the second greatest influence on similar cables on the back of cable tower, their cable forces are reduced. Other relevant cables are replaced, the impact of the cable is relatively small. During the construction period of cables replacement, the girder alignment and displacement at the top of the tower approximate change periodically. According to the principle of optimization, the finally completed cable force that is measured is basic consistent with its theoretical value, the maximum error is about 1%.

optimization; cable stayed bridge; cable replacement; process

10.19713/j.cnki.43−1423/u.2018.10.016

U442.5+；U445.6

A

1672 − 7029(2018)10 − 2565 − 09

2017−08−26

国家自然科学基金资助项目(51378514)

张家生(1964−)，男，湖南长沙人，教授，博士，从事土木工程设计与施工仿真研究；E−mail：zjsdj@mail.csu.edu.cn