基于加速度响应优化大吨位冲击载荷的方法研究

许平，屈秋云，姚曙光，张德洪，李本怀，刘志祥



基于加速度响应优化大吨位冲击载荷的方法研究

许平1，屈秋云1，姚曙光1，张德洪1，李本怀2，刘志祥3

(1. 中南大学 轨道交通安全教育部重点实验室，湖南 长沙 410075； 2. 中国长春轨道客车股份有限公司，吉林 长春 220100； 3. 西南交通大学 电气工程学院，四川 成都 610013)

利用面板的加速度响应反求出面板所受的载荷力时间历程，首先，开展测力墙面板在台车冲击载荷下的试验，建立有限元仿真模型得获得一条初始的载荷力时间曲线，然后在满足仿真与实验的测力面板加速度响应差异最小的目标下，采用遗传迭代算法优化反求出作用在测力面板的一条最优的力时间曲线。最后通过试验验证，说明采用反求方法获得的测力板所受的载荷具有较好的适用性，该方法可以推广到测量铁路车辆的用组合式测力墙测量大吨位碰撞力。

大吨位；载荷识别；仿真；优化反求

耐冲击吸能安全列车是世界各国解决车辆被动安全防护技术的重要手段，车辆碰撞试验是评估耐冲击吸能列车的重要方法。作为车辆碰撞试验中不可缺少的大吨位测力墙，其测量的准确性直接影响耐冲击车辆耐冲击车体的评估可靠性[1]。由于轨道车辆碰撞时质量大、运行速度高、撞击截面大等特点，导致出现大吨位冲击力，数值可达870 kN，而技术成熟、应用广泛的测力传感器量程一般不超过700 kN，极易造成局部传感器超载，而且造价昂贵[2]。并且在汽车碰撞领域的碰撞测力墙的研究比较成熟，但是试验大多数用到的是压电式测力传感器，量程仅为20 kN[3]。所以，仅仅依靠传感器测量冲击载荷可靠性不高，亟待寻求一条载荷识别的新技术，确保在刚性墙碰撞试验中准确地识别动载荷。为了解决试验中碰撞位置偏离传感器中心导致测力不准的问题，汽车领域提出了建立测力单元的组合式测力墙方案。轨道车辆碰撞截面通常比较大，而且不同撞击位置的刚度差别很大，若在轨道车辆碰撞试验中采用传统分块式面板的测力墙，必将使用大量传感器，因此非常有必要对测力墙结构进行合理组合设计，以满足测试需求。Tolman[4]针对轨道列车事故重现提出用组合式单元测力墙分析方法的可行性。张德洪等[5]基于汽车分块式碰撞面板测力墙，对轨道车辆碰撞试验大吨位测力墙的方案进行研究，提出分块式和整块式面板组合的测力墙结构设计方案。并说明传感器数量、传感器间距和面板厚度对组合式面板测力墙的结构测试结果有影响。确定动载荷的方法一般分为直接测量方法和识别方法两大类。工程实际中，当轨道车辆承受大吨位的冲击载荷等情况下，结构的外载荷很难用传感器直接测量，因而必须利用载荷识别技术来确定。载荷识别即根据已知结构的动态特性和实测的动力响应(位移、速度、加速度或应变等)求解作用在结构的动态载荷。主要的方法分为频域法和时域法[6]。频域法：Bartlett等[7]把载荷识别理论首次应用在航空飞机上，到1984年国内也在航空领域上开始起步研究。Hansen[8]发现在共振区附近存在病态性，以最大列和范数去估计条件数，表明载荷识别的误差随载荷数目增加而加大。频域法比较成熟，其动态标定简单，但要求信号样本具有一定的长度，故一般只适用于稳态动载荷或随机载荷，不适应于冲击型瞬态载荷的识别。时域法：Desanghere等[9]提出模态坐标变换的新方法，在时域范围内的进行动态载荷识别。毛玉明等[10]提出一种基于基函数时域展开的动态载荷识别技术，并假定动态载荷离散为一阶跃函数，将载荷识别问题转化为求解基函数权系数的反演问题，有效地识别了作用于无人机机翼上的冲击载荷。LIU等[11]为研究结构动态载荷识别问题提出了一种称为时域有限元离散(TDGM)的新方法。TDGM可以有效地克服噪声的影响,提高动载荷识别的准确性。YAN等[12]将冲击载荷时间历程用一组适当的参数来表示，将时域内的载荷识别问题转换为参数识别问题，最小化冲击响应模型计算结果与实际量测变形之间的差别，通过智能优化方法自适应地识别出载荷时间历程的参数。时域动载荷识别技术尚不完善，识别精度不甚理想，而且稳定性、鲁棒性均有待提高[6]。上述方法主要针对薄板进行研究，而对在工程上应用较广的测力板上的研究较少。而且轨道车辆碰撞测力墙的研制刚刚起步。测力墙是由若干个并排的测力传感器组成的刚性墙面，常见的碰撞测力墙主要由测力传感器、安装背板和碰撞面板组成，若干测力传感器单元(Load Cell)组成分块形式的测力墙[13](Load Cell Wall)。本文探讨一种通过测量测力面板上布置的加速度响应，反求出测力面板承受的冲击载荷的研究方法。利用一块面板可以实现由加速度响应反求出小吨位的冲击载荷，以此类推，多块面板组合起来，就可以实现由加速度响应反求出大吨位的冲击载荷。

1 实验设计

1.1 动态响应试验

实验模拟台车撞击测力面板，台车前端焊接一根吸能圆管，质量12.65 t的台车以 1.712 m/s的初速度撞击刚性墙，测速仪记录了冲击的速度，布置2台高速摄影，分别布置于试件的正上面和侧面，用来捕捉吸能圆管碰撞时刻的变形形式和记录试件的压缩量，得到试件的位移时间曲线[14]。测力墙由一块匀力板以及其后面布置1个传感器组成。4个测点采集加速度信号，测量纵向冲击加速度。各测试设备和加速度传感器布置如图1。

图1 试验设备布置

1.2 实验结果

测力面板承受圆管冲击载荷试验的目的是通过测量测力面板受载荷影响产生的加速度来反求测力面板承受的载荷响应。试验测得加速度响应和载荷力，分别采用60 Hz[15]和180 Hz[16]的SAE过滤方法对其进行滤波，曲线如图2所示。

图2 加速度计测得的加速度曲线和测力传感器测得的力时间曲线

2 有限元建立

2.1 有限元建立

试验模拟安装在台车上的吸能圆管撞击测力面板。用带质量(12.65 t)带速度(1.712 m/s)的简化的台车代替试验台车。1个碰撞面板横截面均为200 mm×200 mm的长方形，厚度为40 mm，在截面均布有12个用于连接碰撞面板与传感器的沉头孔。测力传感器近似于一个圆柱体，两端挖出8个M16螺栓孔，一端通过螺栓与碰撞面板连接，另一端通过背板与刚性墙相连固定，实物图如图3。

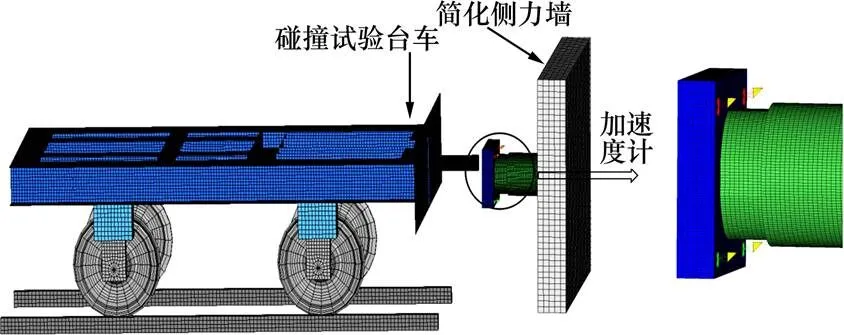
图3 圆管冲击测力板的有限元模型

采用测力面板及传感器分别采用3 mm和6 mm的六面体实体网格进行划分，一共有197 769个单元，219 049个节点。测力传感器在碰撞过程中几乎不发生变形，采用高强度钢，屈服强度取Q1200；测力面板用于承受冲击力，产生微小变形，取屈服强度800 MPa。根据实际情况，2构件都选用了弹塑性材料(*MAT_PLASTIC_KINEMATIC)进行仿真模拟。将传感器和测力墙面板用螺栓进行预紧力连接。碰撞面板及传感器之间的连接关系可通过定义LS_DYNA关键字“CONTACT_ ANTOM- ATIC_SURFACE_TO_ SURFACE”的绑定接触来模拟。传感器连接的混凝土墙的一端静止不动，对其节点集施加3个方向的固定约束。在相对应位置布置加速度计读取面板的微小加速度响应。

2.2 有限元结果

与试验结果相比较，分析有限元仿真的有效性。变形结果如图4。圆管的变形模式呈轴对称模式，产生3个半褶皱，与圆管碰撞试验后的变形基本一致。仿真和试验的力时间曲线趋势大致相同，试验测量的和仿真的面板加速度曲线如图5。

图4 变形序列图

图5 仿真和实验对比的力时间曲线和加速度

从图5可以看出，不管是仿真和试验的载荷力时间曲线还是加速度曲线，其趋势大致相同，但是曲线存在着相位差以及曲线峰值点有差异。所以接下来考虑从相位和峰值力上对曲线进行优化。

3 测力墙面板所受冲击载荷(f_t曲线)优化反求

3.1 反求流程

基于测力板变形反求面板载荷响应反求流程：

1) 基于吸能圆管冲击测力面板的试验，圆管产生对称圆环模型，并利用有限元方法估算(-曲线)参数初值；

2) 进行有限元仿真计算，得出给定(曲线)载荷作用下测力墙面板加速度的模拟结果；

3) 计算仿真模型和碰撞试验测力板上的测试点的加速度结果之间的差异，并且判断是否满足收敛条件，如果满足收敛条件则反求结束，如果不满足则由优化算法重新给出新的载荷曲线，进行新一轮数值模拟计算，直到满足收敛条件，所得到的最优解即为反求的载荷曲线。

上述整个反求过程可用图6表示。整个流程可分为正问题和反问题 2 个部分[17]，其中正向分析是指给定载荷作用下(曲线)计算测力面板测点的加速度响应的过程，由有限元数值模拟来完成；反问题分析是指采用遗传优化算法不断改变曲线参数，直到迭代满足收敛条件。通过hyperstudy和hypermesh软件接口程序或命令实现这两个正反向过程的无缝集成。

3.2 优化算法选择

3.2.1 设计变量的选择和初始化

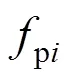
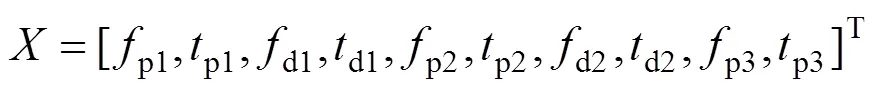
第个波峰的和第个波谷的载荷力和对应时间点表达式表示如下：

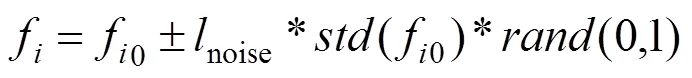
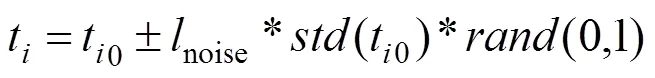
注：和分别是载荷曲线的最高点和平均载荷力；是有限元仿真得到的载荷曲线在波峰波谷处的载荷值，即峰值点的初始值。

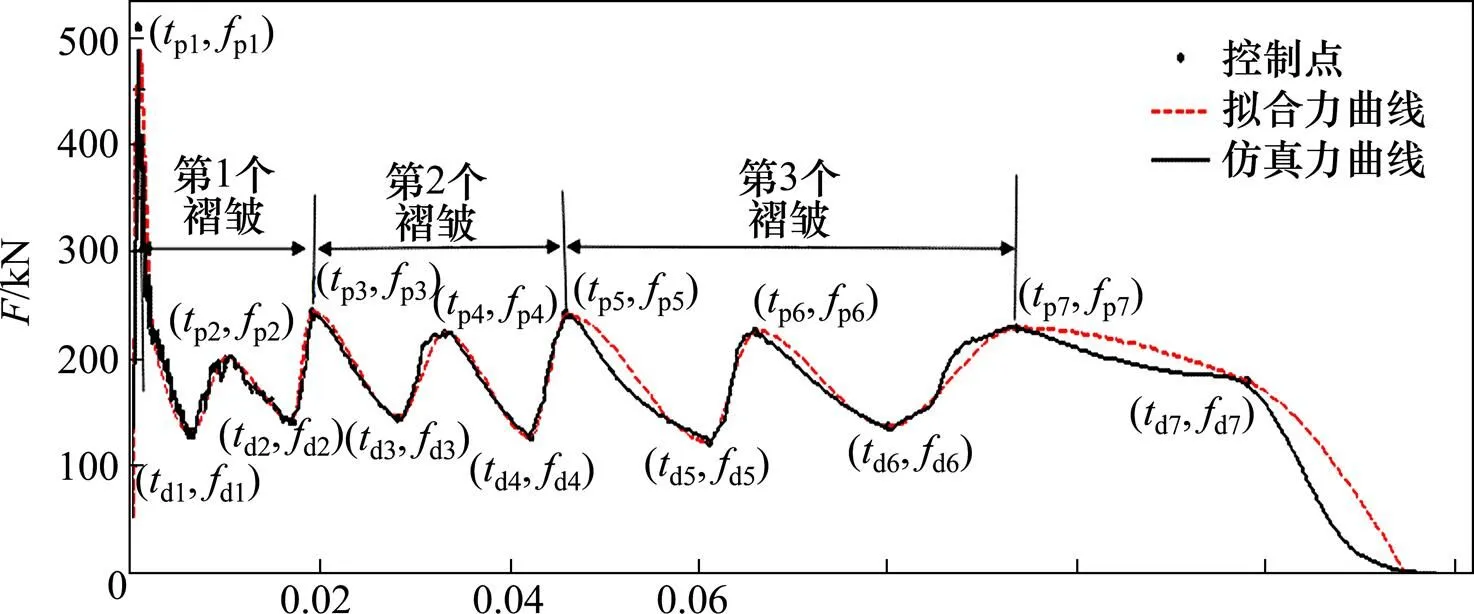
图7 由有限元仿真确定初始的载荷时间曲线

3.2.2 目标函数的选择

有限元仿真取具有代表性的与试验相对应的4个加速度计，如图7的1~4个点。构造了理论值与实验值之间的差异作为目标函数，优化的过程就是使差异最小化：

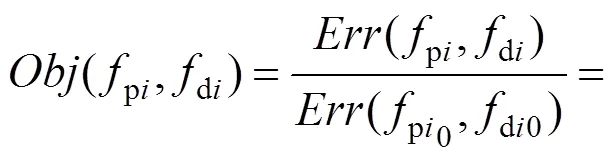
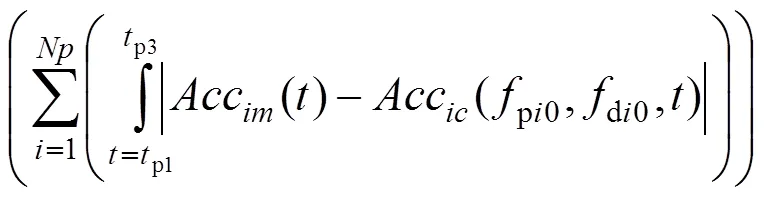
式中：和(p1~p3)分别表示测力板上布置的加速度个数和力曲线在产生第1个褶皱的时间域，Acc和Acc分别表示试验结果和模拟仿真的加速度响应值。

3.2.3 变量对结果的敏感性分析

变量初值的选取直接关系到优化迭代算法的收敛性。本文采用有限元仿真将参数化结果作为初值，并根据初值确定搜索空间，由于试验的变量较多，通过灵敏度分析还可以决定哪些不可控因子对系统或模型的输出有较大的影响[19]。剔除影响不大的参数，选取影响较大的参数作为自变量的研究参数。提高摸型的运算效率，节约计算时间。样本点和目标值如表1。

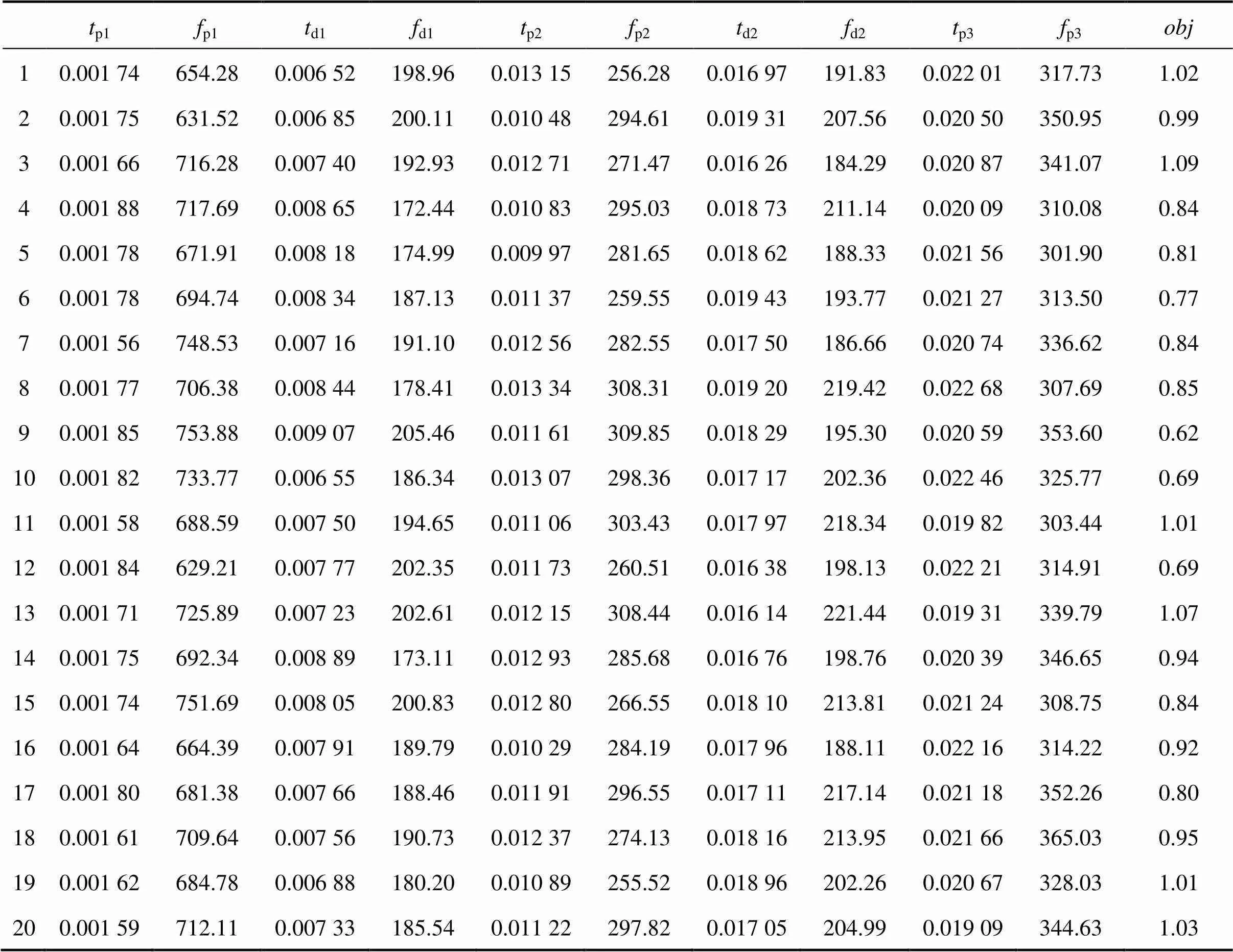
表1 DOE1设计的样本点

折线斜率越大，代表该因子对响应的影响程度越大，如图8可以看出，这10个变量因子对于该响应值的影响程度，所以，变量p1，d1，d2，d2，p3和p3对相应的影响程度较大，所以筛选掉不重要的变量，重点研究变量p1，d1，d2，d2，p3和p3。

3.2.4 实验设计(DOE)

试验设计是构建近似模型的基础，它是通过合理取样方法，在设计域内选取有限个数量的样本点，以较小的规模进行试验，得到整个设计域内设计变量和响应值之间的相互关系。试验设计中常用方法包括全因子设计、部分因子设计、中心组合设计以及Box-Behnken设计；以及正交试验设计、D-最优设计、均匀设计以及拉丁超立方/最优拉丁超立方设计，考虑到试验参数比较多，文中采用的(Box-Behnken设计和拉丁超立方设计)作为采样方法[20]，表2为由拉丁超立方产生的研究参数的30个样本点分布。

图8 控制变量的主效应图

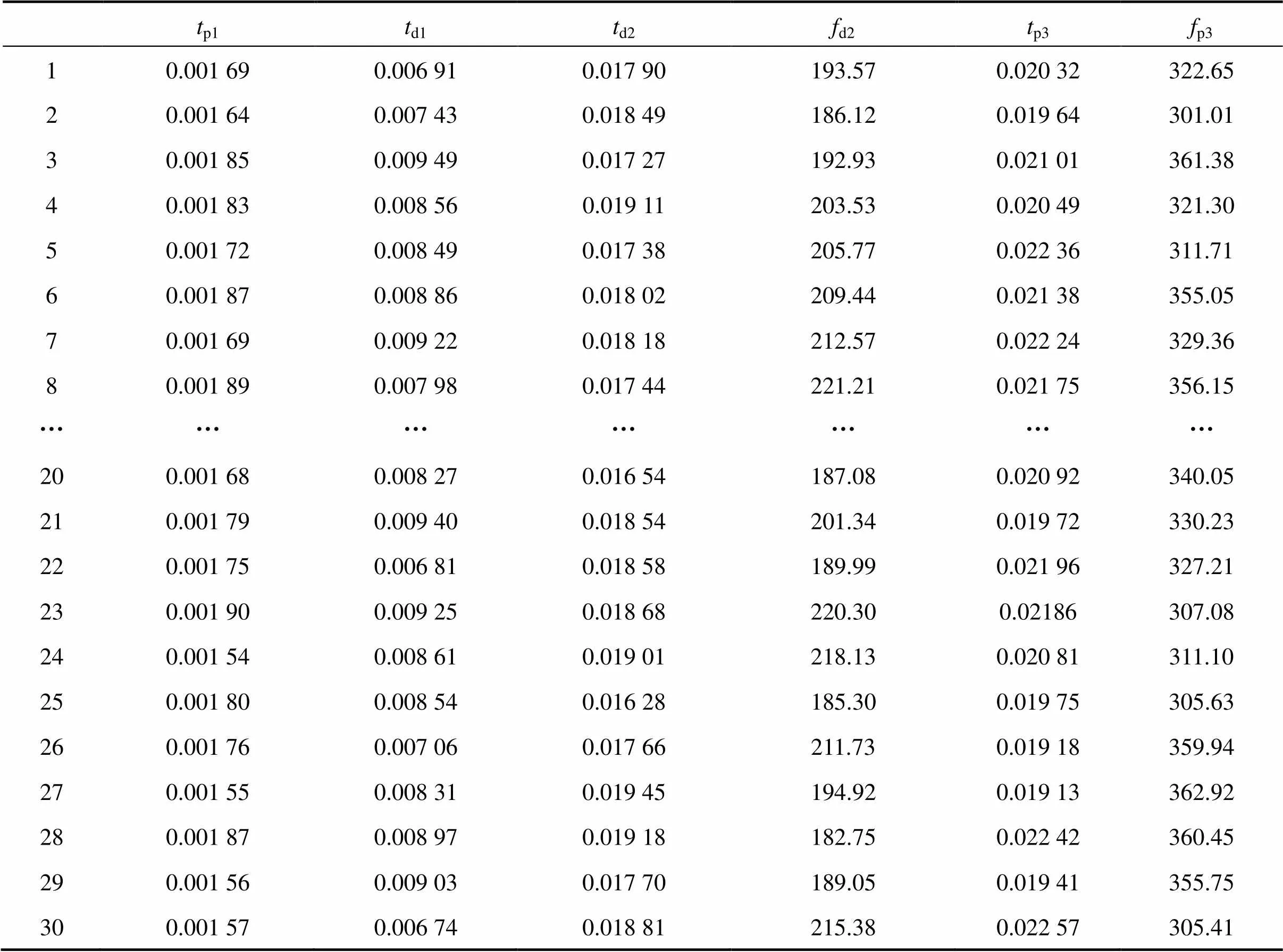
表2 DOE2设计的检验样本点

3.2.5 近似模型和误差估计

近似方法对少量的几组输入变量(设计变量)和输出变量(目标函数)之间的关系进行近似，即用数学的方法对输入变量和输出响应的拟合或插值，去预测参数在其他点处的实验结果。Hyperstudy中提供了最小二乘法(LSR)、移动最小二乘发法(MLSR)和Kriging 3种方法。本文采用响应面方法(RSM)方法对模型进行近似[20]。描述载荷与加速度响应之间关系的不同阶数(线性、2阶和3阶)的代理模型结果如式(2)~(4)。

线性拟合：

1=1.021+(−286.996*p1^1)+(−8.279*d1^1)+

(−3.386*d2^1)+(−8.374*p3^1) (2)

二阶拟合：

2=0.653+(7 493.687*p1^1)+(−286.275*d1^1)+

(−164.160*d2^1)+(0.008*d2^1)+(−213.199*p3^1)+

(−0.016*p3^1)+(−2 529 687.820*p1^2)+(5 737.316*

d1^2)+(9 288.616*d2^2)+(4 381.883*p3^2)+

(17 497.849*p1^d1)+(−24 208.192*p1^d2)+(3.602*

p1^d2)+(27 677.331*p1^p3)+(−0.284*p1^p3)+

(−2 881.321*d1^d2)+(0.651*d1^d2)+(691.744*

d1^p3)+(0.188*d1^p3)+(−0.355*d2^d2)+

(−1 374.347d2^p3)+(−0.008*d2^p3)+(−0.044*

d2^p3)+(0.017*p3^p3) (3)

三阶拟合：

3=−4.195+(30 387.822*p1^1)+(−675.444*d1^1)+

(−2 898.217*d2^1)+(0.470*d2^1)+(−3898.038*

p3^1)+(−0.016*p3^1)+(−15 821 528.119*p1^2)+

(68 385.801*d1^2)+(163 309.596*d2^2)+(−0.002*

d2^2)+(1 790 557.125*p3^2)+(12 856.500*p1^d1)+

(−3 526.301*p1^d2)+(1.751*p1^d2)+(29 462.736*p1^

p3)+(0.305*p1^p3)+(−4 840.651*d1^d2)+(0.575*d1^

d2)+(−75.069*d1^p3)+(0.111*d1^p3)+(−0.168*d2^

d2)+(−3 556.230*d2^p3)+(−0.027*d2^p3)+(0.027*

d2^p3)+(0.071*p3^p3)+(2 545 484 258.777*p1^2)+

(−2 652 678.720*d1^2)+(−2 890 668.415*d2^2)+

(−2 478 799.983*p3^2)+(−0.000*p3^2) (4)

对模型近似的拟合结果，进行相关系数、均方根和相对误差的分析[20]。如表3可以看出，阶数越高拟合效果越好，并且二阶方法的2超过90%，说明模型拟合的效果较好。可选二阶响应面模型能够很好的近似载荷参数与加速度响应之间的关系。

3.2.6 优化算法以及优化结果

关于优化问题求解，以前研究文献中大多采用传统的基于梯度的优化方法，譬如 Levenberg- Marquardt(LM)法，但是该方法经常会出现局部收敛的现象并且初始值的选取对结果的影响较大，经常会遇到困难。因此，本文采用遗传算法的策略。遗传算法是根据生物进化过程开发的一种全局优化随机搜索算法，它借鉴生物界中的遗传进化和自然选择机制。

表3 近似模型拟合误差表阶数

算法应用广泛，具有极好的鲁棒性，所以在解决优化问题时，首选遗传算法。算法基本程序流程：遗传算法首先产生一组初始的随机值，然后开始搜查，进行概率选择，把个体的适应度作为目标值进行计算，即适应值大的个体，选择概率大；反之亦然，适应度小的被淘汰；再通过变异和交叉等方式，产生新个体，组成新一代种群，一代一代，积累下来，直到最终算法收敛于一定值，即得到优化的解，如表4。

表4 遗传算法参数设置

4 面板载荷响应优化反求结果

采用遗传算法对载荷进行优化反求，反求参数的结果表5所示。再与优化反求的载荷曲线进行对比，如图9。

如表6，以试验测量的载荷力为标准，在第1个峰值力处，有限元方法的误差为17.38%，二阶优化后的误差分别为1.01%和4.65%；相同，第2个和第3个峰值力，有限元方法的误差为4.45%和2.82%，二阶优化后的误差为3.12%和1.67%。说明载荷曲线优化反求效果比较好。

表5 优化反求的参数和响应的结果

表6 优化的载荷曲线与试验曲线峰值力的误差对比

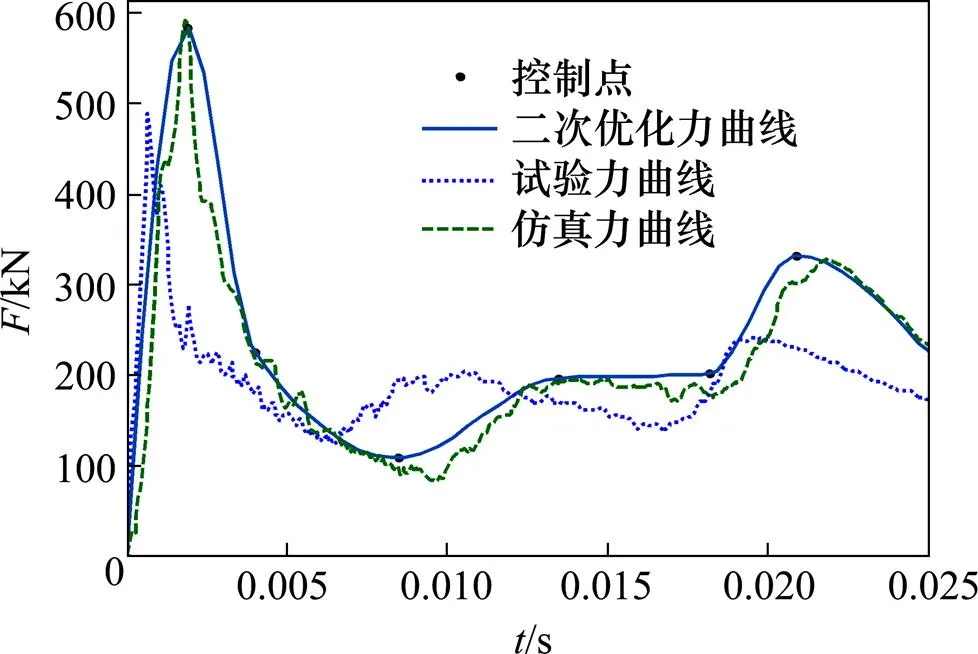
图9 优化的载荷曲线与试验曲线对比

5 结论

1)直接用有限元进行仿真得出的数值解有较大的误差，通过优化反求能大大减少误差。正问题与反问题的结合能大大提高解的准确性。

2) 实现了通过测力板变形情况预测出面板受到的载荷大小的方法，一方面在传感器出现故障问题时可以起到临时测力的作用，另一方面，可以验证传感器测力的准确度。

3) 推广意义：由反求识别简单的圆管载荷可以推广到其他复杂试件的冲击载荷；由反求出分块面板的时间曲线，推广到多块组合面板的时间曲线，直到推算得到应力云图。

[1] 郑祖丹, 胡伟强, 吴斌, 等. 汽车碰撞测力墙的研制[J].上海汽车, 2011(10): 22−27. ZHENG Zudan, HU Weiqiang, WU Bin, et al. Development of impact force wall about automobile[J]. Shanghai Automotive, 2011(10): 22−27.

[2] 邵恒, 许平, 姚曙光. 轨道车辆碰撞试验大吨位测力墙结构设计研究[D]. 长沙: 中南大学, 2016. SHAO Heng, XU Ping, YAO Shuguang. Study on design of large tonnage force measuring wall for collision test of rail vehicle[D]. Changsha: Central South University 2016.

[3] 吴斌, 朱西产, 郑祖丹, 等. 汽车碰撞测力墙的研制与评估[C]// 重庆: 中国汽车工程学会第13届汽车安全技术年会, 2010. WU Bin, ZHU Xichan, ZHENG Zudan, et al. Development and evaluation of impact force wall about automobile[C]// Chongqing: The 13th Conference of Automotive Safety Technology, 2010.

[4] Tolman S S. Analysis of load cell barrier data for accident reconstruction applications[D]. University of Utah, 2008.

[5] 许平, 张德洪, 邵恒, 等. 轨道车辆碰撞试验大吨位测力墙结构设计研究[J]. 铁道科学与工程学报, 2017, 14(11): 2435−2443. XU Ping, ZHANG Dehong, SHAO Heng, et al. Study on structural design of large tonnage force measuring wall for collision test of rail vehicle[J]. Journal of Railway Science and Engineering, 2017, 14(11): 2435−2443.

[6] 周盼, 张权, 率志君, 等. 动载荷识别时域方法的研究现状与发展趋势[J]. 噪声与振动控制, 2014(1): 6−11. ZHOU Pan, ZHANG Quan, SHUAI Zhijun, et al. Review of research and development status of dynamic load identication in time domain[J]. Noise and Vibration Control, 2014(1): 6−11.

[7] Bartlett F D, Flannelly W G. Model verication of force determination for measuring vibratory loads[J]. Journal of the American Helicopter Society, 1979, 24: 10−18.

[8] Hansen P C. Rank-deficient and discrete ill-posed problems: Numerical aspects of linear inversion[J]. American Mathematical Monthly, 1998, 4(5): 491.

[9] Desangherc G, Snoeys R. Indirect identification of excitation forces by modal coordinate transformation [C]// Orlando: Proceedings of the 3rd IM AC, 1985: 685−690.

[10] 毛玉明, 林剑锋, 刘靖华, 等. 基于动态质量分析的飞行器结构振动试验载荷与环境条件分析[J]. 振动与冲击, 2016, 35(16): 1−5. MAO Yuming, LIN Jianfeng, LIU Jinghua, et al. Analysis of load and environmental conditions of aircraft structures based on dynamic mass analysis[J]. Journal of Vibration and Shock, 2016, 35(16): 1−5.

[11] LIU Jie, MENG Xianghua, JIANG Chao, et al. Time-domain Galerkin method for dynamic load identification[J]. International Journal for Numerical Methods in Engineering, 2016, 105(8): 620−640.

[12] YAN Gang, ZHOU Li. Impact load identification of composite structure using genetic algorithms[J]. Journal of Sound and Vibration, 2008, 319(3): 869−884.

[13] WANG Linjun, CAO Huiping, HAN Xu, et al. An efficient conjugate gradient method and application to dynamic force reconstruction[J]. Journal of Computational Science, 2015(8): 101−108.

[14] 杨兆建, 王勤贤. 测力传感器研究发展综述[J]. 山西机械, 2003(1): 1−3. YANG Zhaojian, WANG Qinxian. Analysis of research and development of force sensor[J]. Shanxi Machinery, 2003(1): 1−3.

[15] ISO 6487—2012, 道路列车—冲击试验中的测量技术—测试仪器[S]. ISO 6487—2012, Road vehicles—Measurement techniques in impact tests—Instrumentation[S].

[16] DIN EN 15227: 2008—07, 铁路设施. 铁路车辆车身的防撞性要求[S]. DIN EN 15227: 2008—07 railway applications- crashworthiness requirements for railway vehicle bodies [S]

[17] Abranowicz W, Jones N. Dynamic axial crashing of circular tubes[J]. International Journal of Impact Engineering, 1984(2): 263−281.

[18] 郝长岭, 周贤宾, 李志光, 等. 紧缩场蜂窝夹层反射面板材料参数优化反求[J]. 北京航空航天大学学报, 2013(3): 190−196. HAO Changling, ZHOU Xianbing, LI Zhiguang, et al. Design of material parameters of reflective field honeycomb sandwich reflective panel[J]. Journal of Beijing University of Aeronautics and Astronautics, 2013(3): 190−196.

[19] Ebrahimi S, Vahdatazad N. Multi objective optimization and sensitivity analysis of honeycomb sandwich cylindrical columns under axial crushing loads[J]. Thin- walled Struct, 2015, 88: 90−104.

[20] 洪清泉. OptiStruct & HyperStudy理论基础与工程应用[M]. 北京: 机械工业出版社, 2013: 337−362. HONG Qingquan. OptiStruct & HyperStudy theoretical basis and engineering application[M]. Beijing: Machinery Industry Press, 2013: 337−362.

(编辑 阳丽霞)

The method research to reverse the big tonnage impact load based on acceleration response

XU Ping1, QU Qiuyun1, YAO Shuguang1, ZHANG Dehong1, LI Benhuai2, LIU Zhixiang3

(1. Key Laboratory of Traffic Safety on Track Ministry of Education, Central South University, Changsha 410075, China; 2. CRRC Changchun Railway Vehicles, Co, Ltd, Changchun 220100, China; 3. Southwest Jiaotong University School of Electrical Engineering, Chengdu 610013, China)

In this paper, the acceleration response of the panel is used to calculate the time history of the load on the panels. Firstly, a test on the load wall panels is carried out under car’s impact load, and gain an initial load time curve by means of finite element simulation. And then under the condition that the acceleration response of the force panel is the least difference between simulation and experiment, an optimal force time curve is obtained by using the genetic iterative algorithm. Finally the validation of test illustrates that the reverse method to measure the load on board has good applicability, this method can be applied to measure collision force of large tonnage of railway vehicle by the combined load wall.

large tonnage; load identification; simulation; optimize and reverse

10.19713/j.cnki.43−1423/u.2018.10.023

U279.5

A

1672 − 7029(2018)10 − 2621 − 10

2017−07−22

国家自然科学基金资助项目(51675537)；国家科技支撑计划资助项目(2015BAG12B01)；教育部重点资助项目(113051A)；国家重点研发计划资助项目(2016YFB1200505-016)

姚曙光(1970−)，女，湖南邵阳人，副教授，博士，从事车辆结构设计研究；E−mail：ysgxzx@csu.edu.cn