跨中交叉布索的多塔斜拉桥受力机理及参数分析

陈恒大，姚丝思，邬晓光

跨中交叉布索的多塔斜拉桥受力机理及参数分析

陈恒大1，姚丝思1，邬晓光2

(1. 陕西省土地工程建设集团，陕西 西安 710075； 2. 长安大学 公路学院，陕西 西安 710064)

为解决多塔斜拉桥整体刚度不足的力学缺陷，研究跨中交叉布索多塔斜拉桥的力学特性，分析交叉索的作用机理，得出交叉索作用下中塔抗推刚度的理论公式，并以昆斯费里大桥为依托工程，通过改变跨中交叉拉索对数进行各方案的有限元分析，研究交叉索参数对结构刚度的影响程度及规律。研究结果表明：跨中交叉拉索使主梁挠度减小，结构整体刚度增大；在50 kN/m的不平衡荷载作用下，设置6对交叉索使中塔水平位移减小约28.63%，边塔水平位移减小约14.16%，跨中挠度减小约13.26%，主梁最大正弯矩减小约29.80%，主梁最大负弯矩减小约17.41%；多塔斜拉桥整体刚度随交叉索数量的增加而增大，但刚度增大趋势逐渐减缓。

桥梁工程；多塔斜拉桥；交叉索；受力机理；参数分析

随着全球一体化的进展和跨江、跨海大桥的兴起，多塔斜拉桥渐渐成为桥梁界的新宠儿[1−2]。自1962年诞生的采用巨大刚性桥塔的Maracaibo Bridge开始，到目前在建的采用中跨跨中交叉布索的Queensferry Crossing为止，几乎所有的多塔斜拉桥都从不同角度采取各类措施增大非边塔刚度从而达到提升结构整体刚度的目的[3−4]，这足以说明多塔斜拉桥非边塔刚度不足是限制其发展的最重要因素。陈恒大等[5]对多塔斜拉桥的纵向抗推刚度进行了公式推导，并结合国内外几座典型桥梁探讨工程实际中提升多塔斜拉桥桥塔纵向抗推刚度的措施；Tang[6]整理了国内外已通车和在建的多座多塔斜拉桥刚度提升措施，并提出了相关建议和补充；石雪飞等[7−8]利用有限元方法分析了桥塔刚度、拉索刚度和加劲索初张力等因素对多塔斜拉桥整体刚度的影响；李忠三[9]依托有限元模型对多塔斜拉桥竖向刚度随桥塔数量变化的规律进行了研究，提出了在塔梁结合处设置双排支座增加桥塔刚度的方案。综上所述，有关多塔斜拉桥刚度提升的大多数研究是依据有限元模型的仿真计算而进行的，很少有从力学角度对多塔斜拉桥的刚度特征进行理论分析，本文以总结多塔斜拉桥各类加劲体系的结构特点为前提，对跨中交叉布索多塔斜拉桥的交叉索作用机理进行了力学分析，并以昆斯费里大桥为依托工程，分析交叉索设置方案的改变对多塔斜拉桥主要力学指标的影响，为跨中交叉布索的多塔斜拉桥概念设计提供参考。

1 加劲索体系

Gimsing等[2, 6−7]对多塔斜拉桥的加劲索体系进行了研究，主要有以下几种加劲措施，如图1所示。

1.1 水平加劲索

如图1(a)中所示，水平加劲索的理念是使各桥塔塔顶纵向偏位保持一致，石雪飞等[7−8]也用有限元模拟的手段对多塔斜拉桥水平加劲索的力学指标进行了分析，水平加劲索垂度效应显著，加劲效果明显降低，一般不予采用。

1.2 倾斜加劲索

如图1(b)中所示，多塔斜拉桥采用倾斜索加劲时会使边近塔处产生较大的弯矩，石雪飞等[7−8]使用有限元模拟的手段对多塔斜拉桥水平加劲索的力学指标进行了分析，倾斜加劲索垂度效应显著，中等跨径的多塔斜拉桥比较适用。

1.3 跨中交叉索

如图1(c)中所示，跨中交叉索的加劲机理是使各桥塔共同承担荷载，其加劲方式简洁明快，更易于接受。Gimsing[2]通过对交叉索的定性分析，认为此方式明显优于前2种加劲索形式。陈艾荣等[8]提出交叉索体系存在最优交叉索数量；石雪飞等[7−8]也用有限元模拟的手段对多塔斜拉桥跨中交叉索的力学指标进行了分析，认可了其加劲效果，但交叉索对数以及交叉段主梁长度占主跨的比例等需要深入研究。

1.4 下拉索

如图1(d)中所示，下拉索相当于双塔斜拉桥的端锚索对桥塔的约束，对于斜拉桥的主梁轴向压力过大这一弊端无疑是雪上加霜，且下拉索较短、应力幅大，耐久性弱。尽管有学者做了有限元模拟分析[10]，证明了下拉索加劲多塔斜拉桥有一定效果，但从受力和美观两方面考虑，此方案皆不是好的选择。

将各加劲索的加劲效率做对比，可为多塔斜拉桥加劲措施的实施提供参考，具体见表1。

表1 各加劲索体系计算结果

分析可见，水平加劲索改变了斜拉桥的轻盈感，一般不建议采用；倾斜加劲索较易于接受，但过长的倾斜加劲索具有较大的垂度效应，加劲效果并不十分理想；下拉索导致斜拉桥主梁轴力增大是其最大缺陷，且美观上也影响了斜拉桥的轻盈雅致；跨中交叉索的加劲机理是通过交叉索的连接作用使各桥塔共同承担荷载，虽然没有水平索加劲立竿见影，但其加劲方式简洁明快，更易于接受。下文将对多塔斜拉桥交叉索的作用机理进行研究。

2 交叉索作用机理

取多塔斜拉桥跨中处为研究对象，由图2所示，拉索1的索力变化Δ1的竖向分力为Δ1y，其一部分被拉索2索力变化的竖直分力Δ2y平衡，另一部分使得主梁产生向上的挠曲变形。该处力学分析清晰的反映了跨中交叉索的作用机理，在传统斜拉桥中，拉索1的竖向分力Δ1y完全用来使得主梁发生挠曲变形，结构将产生较大的形变，而在交叉索多塔斜拉桥中，当中塔发生纵向位移时，梁段的重量在交叉背索中重新分配，使得拉索1索力增大Δ1，拉索2索力减小Δ2，拉索1的竖向分力Δ1y被拉索2平衡了一部分，使得主梁向上挠曲的力减小为Δ1y−Δ2y，故主梁变形减小，结构刚度增大。

水平外力作用于中塔时，在交叉索的作用下，多塔斜拉桥的结构变形如图3所示。

图2 交叉索作用机理

图3 结构变形及参数图

图3中，1，1为桥塔自身的弹性模量、抗弯惯性矩；2，2为主梁自身的弹性模量、抗弯惯性矩；3，3为斜拉索的弹性模量(此处为采用恩斯特公式修正后的拉索弹性模量)、截面积；为外力作用下中塔水平位移；为外力作用下主梁上挠位移。交叉索索力为1，2，拉索长均为，与主梁的夹角为，桥塔高，桥面以上塔高，主跨跨径为2。

当水平外力作用于中塔时，可以分为1和22部分。1使得中塔在自身刚度下发生变形，2使得拉索1伸长。拉索1近塔端的水平位移由2部分组成，一部分是拉索1自身伸长引起的，另一部分是由于主梁上挠使得拉索1近塔端产生的水平位移。以中塔塔顶为研究对象，根据变形协调原理，1作用下的塔顶水平位移应与2作用下的拉索1近塔端水平位移相等，均等于。

拉索1索力变化带来的影响可以分为2部分，一部分使得主梁上挠，另一部分使得拉索2压缩。忽略边塔塔顶很小的水平位移，以跨中主梁为研究对象，根据变形协调原理，主梁上挠位移与拉索2近梁端竖向位移相等，均等于。

由此建立平衡方程，即可求解的值，进而求得考虑桥塔、主梁自身刚度影响下的交叉索对中塔的约束刚度。进而可求得一对交叉索对中塔抗推刚度的贡献为：

公式(1)即为考虑塔梁自身刚度影响下，多塔斜拉桥跨中交叉索提供的中塔纵向约束刚度估算 公式。

3 工程实例

昆斯费里大桥采用单塔形式桥塔，中塔处塔梁固结，提供全桥纵向约束。在主梁中央布置了2个平行索面，拉索锚固在钢箱梁箱内中间位置，相关尺寸见图4和图5所示。每个主跨有24对斜拉索，其中6对交叉拉索锚固于主梁上[12−13]，形成一个虚拟的桁架系统[14]。

图4 昆斯费里大桥立面图

图5 昆斯费里大桥结构截面图

建立跨径布置为(341+650+650+341) m的三塔斜拉桥模型，采用中塔塔梁固结，边塔塔梁分离的约束形式。模型主要参数为：主梁为钢箱梁，弹性模量2为210 GPa，截面抗弯惯性矩2为6.818 mm4，桥塔为C50混凝土材料，弹性模量1为34.5 GPa，截面抗弯惯性矩1为411.875 mm4，斜拉索为钢绞线，弹性模量3为195 GPa，单根拉索面积为0.011 m2，横桥向为平行双索面。

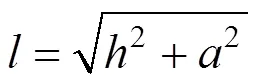
在合理成桥状态下，给中塔塔顶作用一水平外力，其产生的水平位移为Δ，有限元计算过程中考虑了非线性的影响，计算结果见表2所列。

为验证理论解的精确度，通过增加斜拉索，分别设置2~10对跨中交叉索，此处的交叉索材料、截面取斜拉索相同参数，模型细节见图7所示。

单位：m

表2 无交叉索模型计算结果

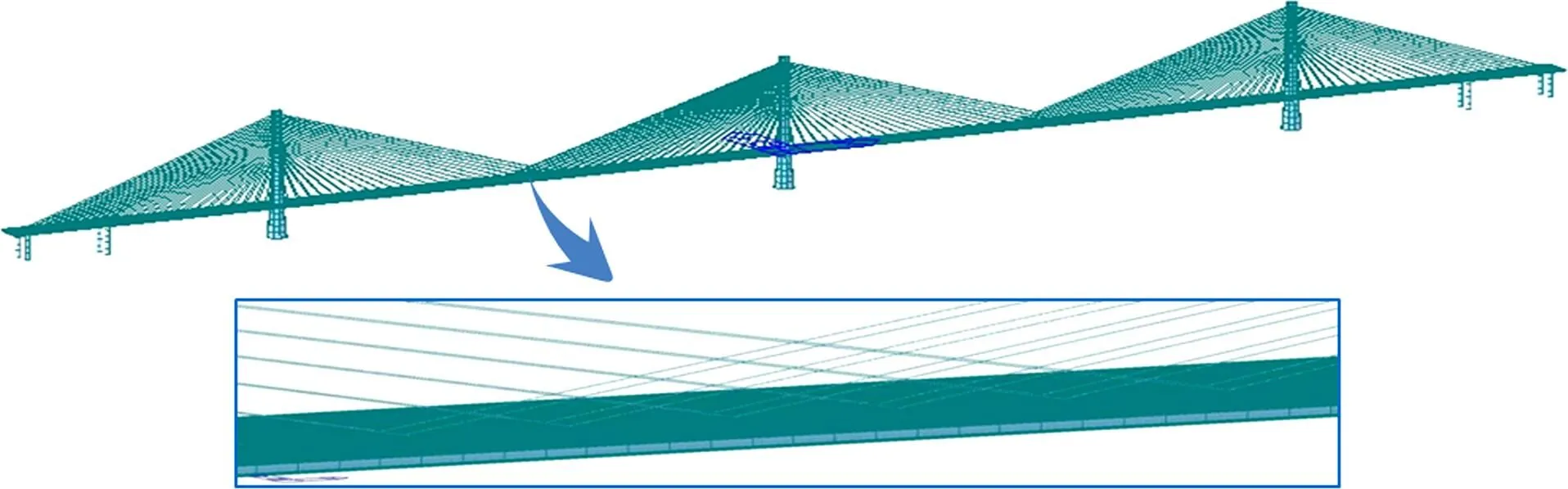
图7 跨中布置六对交叉索三塔斜拉桥模型图

4 交叉索参数变化影响分析

为研究交叉索参数对结构刚度的影响程度及规律，本文基于不设置交叉索的基本模型，将原设计的23对斜拉索在小范围内调整索间距，具体参数见表3所列。

表3 索距参数一览表

交叉索使得在保持斜拉索数量不变的情况下跨中出现0，2，4，6，8和10对交叉索，依此建立有限元模型，共得到6个对比模型A-F，具体见图8所示。

三塔斜拉桥最不利荷载工况为在一侧主跨作用满跨活载，如图9所示，本文采用多工况加载的方式，荷载逐渐递增，以便得到结构刚度的变化规律，共分为5个荷载工况：工况1：恒载+右跨满跨均布载(=10 kN/m)；工况2：恒载+右跨满跨均布载(=20 kN/m)；工况3：恒载+右跨满跨均布载(=30 kN/m)；工况4：恒载+右跨满跨均布载(=40 kN/m)；工况5：恒载+右跨满跨均布载(=50 kN/m)。

图8 跨中交叉布索的三塔斜拉桥模型对比图

图9 活载作用示意图

4.1 桥塔塔顶偏位

依据工况内容对各模型进行加载，将计算结果进行对比分析，如图10~11所示。

图10 中塔塔顶水平位移对比图

图11 边塔塔顶水平位移对比图

由图10和图11可知，随着均布荷载的增加，桥塔塔顶偏位逐渐增大；随着交叉索数量的增多，桥塔塔顶偏位逐渐减小，但每增加单位数量的交叉索，桥塔位移减小速率逐渐变慢。结果表明交叉索能提高桥塔刚度，但随着数量的增多其提升的效率逐渐降低。以跨中设置6对交叉索与不设置交叉索的模型计算结果对比分析为例，在50 kN/m的不平衡荷载作用下，中塔水平位移减小约28.63%，边塔水平位移减小约14.16%。可见交叉索对减小桥塔塔顶位移的效率很高。

4.2 主梁变形

根据有限元模型结果提取主跨跨中挠度，如图12所示。

图12 主跨跨中挠度对比图

由图12可知，随着均布荷载的增大，主跨跨中挠度值基本呈线性增大；随着跨中交叉索数量的递增，主跨跨中挠度逐渐减小，结构刚度逐渐变大；以跨中设置6对交叉索与不设置交叉索的模型计算结果对比分析为例，在50 kN/m的不平衡荷载作用下，跨中挠度减小约13.26%。

4.3 主梁弯矩

将原始的无交叉索模型和上文中5个工况的模型进行对比分析，根据有限元模型结果提取出主梁弯矩，如图13和图14所示。

由图13~14结果可知：

随着均布荷载的增大，主梁最大正、负弯矩值基本呈增大趋势，在50 kN/m的均布荷载作用下，随着交叉索数量的增多，主梁最大正、负弯矩值不断减小。当均布荷载小于30 kN/m左右时，主梁正弯矩最大值随着交叉索数量的增多而增大，当均布荷载大于30 kN/m左右时，主梁正弯矩最大值随着交叉索数量的增多而减小。以跨中设置6对交叉索与不设置交叉索的模型计算结果对比分析为例，在50 kN/m的不平衡荷载作用下，主梁最大正弯矩减小约29.80%，最大负弯矩减小约17.41%。

图13 主梁最大正弯矩对比图

图14 主梁最大负弯矩对比图

5 结论

1) 从力学角度论证了交叉索对多塔斜拉桥的作用机理，即跨中交叉拉索可平衡部分用于提升主梁的竖向力，使得主梁变形减小，进而减小整体结构的变形，提高了多塔斜拉桥的整体刚度。

2) 基于变形协调原理，求解了跨中采用交叉索的多塔斜拉桥中塔抗推刚度估算公式，公式表明交叉索对中塔刚度的影响与其自身刚度、主梁刚度、主跨跨径、桥塔高以及交叉拉索索长有关。

3) 通过建立设置不同数量交叉索的多塔斜拉桥模型，得出交叉索提升结构刚度的规律，随着交叉索数量的增多，结构刚度不断增大，提升效率逐渐减缓。

4) 以昆斯费里大桥为依托工程，通过有限元软件模拟得出：在50 kN/m的不平衡荷载作用下，设置6对交叉索使中塔水平位移减小量高达约28.63%，边塔水平位移减小约14.16%，跨中挠度减小约13.26%，主梁最大正弯矩减小约29.80%，主梁最大负弯矩减小约17.41%，进一步验证跨中交叉拉索对提升多塔斜拉桥整体刚度有重要作用。

[1] 肖汝诚, 姜洋, 项海帆. 缆索承重桥的体系比选[J].同济大学学报(自然科学版), 2013, 41(2): 179−185. XIAO Rucheng, JIANG Yang, XIANG Haifan. Comparison between structural systems of cable supported bridges[J]. Journal of Tongji University (Natural Science Edition), 2013, 41(2): 179−185.

[2] Gimsing N J, Georgakrs C T. Cable supported bridges: concept and design[M]. London: John Wiley & Sons, 1997: 52−68.

[3] Cheung M S, Lou D T, Li W C. Recent developments on computer bridge analysis and design[J]. Progress in Structural Engineering and Materials, 2015, 2(3): 376− 385.

[4] Nagai N, Fujino Y, Yanmaguchi H, et al. Feasibility of a 1 400 m span steel cable-stayed bridge[J]. Journal of Bridge Engineering, 2004, 9(5): 444−452.

[5] 陈恒大, 邬晓光, 姚丝思, 等. 基于变形协调原理的多塔斜拉桥边塔纵向抗推刚度[J]. 铁道科学与工程学报, 2017, 14(2): 40−46. CHEN Hengda, WU Xiaoguang, YAO Sisi, et al. Longitudinal restraint stiffness of the side tower for multi-tower cable-stayed bridge based on the principle of deformation coordination[J]. Journal of Railway Science and Engineering, 2017, 14(2): 40−46.

[6] TANG M C. Multi-span cable-stayed bridges[C]// International Association for Bridge and Structure Engineering Conference, Copenhagen, 1996.

[7] 石雪飞, 孙建渊. 三塔斜拉桥静力性能分析[C]// 重庆: 中国公路学会桥梁和结构工程学会桥梁学术研讨会, 2001. SHI Xuefei, SUN Jianyuan. The static performance analysis of three-tower cable-stayed bridge[C]// Chongqing: The Bridge and Structure Engineering Society Symposium Chinese Institute of Highway Bridge, 2001.

[8] 陈艾荣, 项海帆. 多塔斜拉桥概念设计[C]// 第十三届全国桥梁学术会议论文集. 上海: 人民交通出版社, 1998. CHEN Airong, XIANG Haifan. Design of multi tower cable-stayed bridge concept[C]// Thirteenth National Bridge Academic Conference. Shanghai: People’s Communications Press, 1998.

[9] 李忠三. 基于静动力特性的多塔长跨斜拉桥结构体系刚度研究[D]. 北京: 北京交通大学, 2014. LI Zhongsan. Study on rigidity of long-span cable-stayed bridge with multi-tower based on the static and dynamic characteristics[D]. Beijing: Beijing Jiaotong University, 2014.

[10] 肖明葵, 王肖巍, 刘纲. 多塔下拉索斜拉桥静力荷载试验和计算分析[J]. 土木建筑与环境工程, 2011, 33(1): 43−49. XIAO Mingkui, WANG Xiaowei, LIU Gang. Static load test and calculation on multi-tower cable-stayed bridge with tie-down cables[J]. Journal of Civil, Architectural & Environmental Engineering, 2011, 33(1): 43−49.

[11] 陈恒大. 斜拉桥近似解析方法研究[D]. 西安: 长安大学, 2017. CHEN Hengda. Approximate method for analyzing of cable-stayed bridge[D]. Xi’an: Chang’an University, 2017.

[12] Kite S, Carter M, Hussain N, et al. Design of the Forth replacement crossing, Scotland[J]. Bridge Engineering, 2010, 163.

[13] Carter M, Kite S, Hussain N, et al.Forth replacement crossing: Scheme design of the bridge[J]. Iabse Symposium Report, 2009, 96(6): 107−116.

[14] Kite S, Hussain N, Carter M. Forth replacement crossing-Scotland, UK[J]. Procedia Engineering, 2011, 14: 1480−1484.

(编辑 涂鹏)

The stress mechanism and parameter analysis of multi-tower cable-stayed bridge with crossed cables

CHEN Hengda1, YAO Sisi1, WU Xiaoguang2

(1. Shaanxi Provincial Land Engineering Construction Group, Xi’an 710075, China; 2. College of Highway, Chang’an University, Xi’an 710064, China)

In order to solve the mechanical defects of insufficient stiffness of multi-tower cable-stayed bridge, this paper explored mechanical properties of multi-tower cable-stayed bridge with crossed cables and analyzed stress mechanism of the crossed cables, and then obtained an analytic formula for calculating the longitudinal restraint stiffness of the middle tower of multi-tower cable-stayed bridge with cross stays. According to the Queensferry Crossing as a project case, the finite element analysis of many contrast schemes is established by changing the quantity of the crossed cables and the influence degree and regularities of structural rigidity with crossed cables is investigated. The results show that crossed cables can make the beam deflection decreases, thus increasing the overall stiffness of the cable-stayed bridge; under unbalanced loads of 50 kN/m, the displacement of middle tower reduces about 28.63% after setting 6 pairs crossed cables, at the same time, the displacement of edge tower is 14.16%, the reduction of mid-span deflection is 13.26%, the reduction of maximum positive moment and negative moment of main beam are 29.80% and 17.41% respectively; The overall stiffness of the multi-tower cable-stayed bridge increases with the increase of the number of cross cables, but the stiffness increase trend gradually slows down.

bridge engineering; multi-tower cable-stayed bridge; crossed cables; stress mechanism; parameter analysis

10.19713/j.cnki.43−1423/u.2018.10.014

U441.5；U448.27

A

1672 − 7029(2018)10 − 2549 − 08

2017−08−24

国家自然科学基金资助项目(51308056)；中央高校基本科研业务费专项资金资助项目(201493212002)

邬晓光(1961−)，男，湖北英山人，教授，博士，从事桥梁结构理论分析与工程管理研究；E−mail：viphepan@163.com