基于Hu不变矩特征的铁路轨道识别检测算法
董 昱,郭 碧
(1.兰州交通大学 自动化与电气工程学院,甘肃 兰州 730070;2.兰州交通大学 光电技术与智能控制教育部重点实验室,甘肃 兰州 730070)
伴随着智能化技术和城市轨道全自动运行系统的发展,提出了对于列车前方限界监测的功能需求[1-4]。轨道线作为图像空间内铁路限界范围的参考线,其识别的准确性直接影响着列车对于前方环境范围的感知[5]。在钢轨限界范围内的扣件、应答器、道床以及自然光影等形成的动态复杂且纹理不规则的背景干扰,成为当前制约轨道线检测识别措施鲁棒性和精确性的因素。
近些年来,研究人员主要以特征对比和模板匹配的方法作为结构化道路的视觉识别算法基础[6]。在轨道交通钢轨的检测中,采用基于特征的方法主要是针对钢轨轨枕和道床在相角、边缘特性和局部范围内的灰度及纹理差异来识别出轨道线[7-8],如文献[9]中以轨道线主方向相位特征作为钢轨提取的依据,提出迭代校正检测识别算法。基于特征对比的方法有较高的容错率,但是高频图像帧的连续逐帧识别不仅计算量大,也难以满足实时性要求。基于模板匹配的检测方法根据局部范围内的钢轨形态采用分段直线、样条曲线、二次曲线、高次曲线等描述模型来实现对于轨道线的拟合[10]。如文献[11]通过Bresenham算法完成对直线轨道的数学描述,但铁路的曲线段难以通过直线模型拟合,而可以较准确贴合轨道线走向的高次曲线模型对噪声特征点的扰动更加敏感。
鉴于此,本文提出一种近远景区域分段可切换的数学模型进行钢轨线的检测和拟合。针对连续逐帧固定特征匹配方法在精度和实时性方面较差的问题,本文依据轨道线曲率特性,设置近远景区域。针对近景区直轨特性,通过改进霍夫变换来实现描述;在远景区,引入具有尺度不变特性的Hu矩特征,提出可漂移窗口搜索匹配算法来应对弯轨的旋转尺度变化,从而提高算法的鲁棒性,同时增强算法检测和跟踪的效率。
1 轨道检测算法框架
本文所示算法的实现步骤及所对应的理论方法支撑架构框图如图1所示。算法在初始化过程中完成视频序列帧的预处理及轨道线位置的标定。根据车辆上安装的图像传感器与钢轨位置的固定性,采用标定的近景区轨道线边界点作为起点,通过可漂移窗口搜索算法,以具有尺度不变特性的Hu矩作为相似度量参量完成对钢轨特征点的匹配确定。对钢轨线的自动检测和拟合过程最终依据制定的模型更新和切换规则实现。
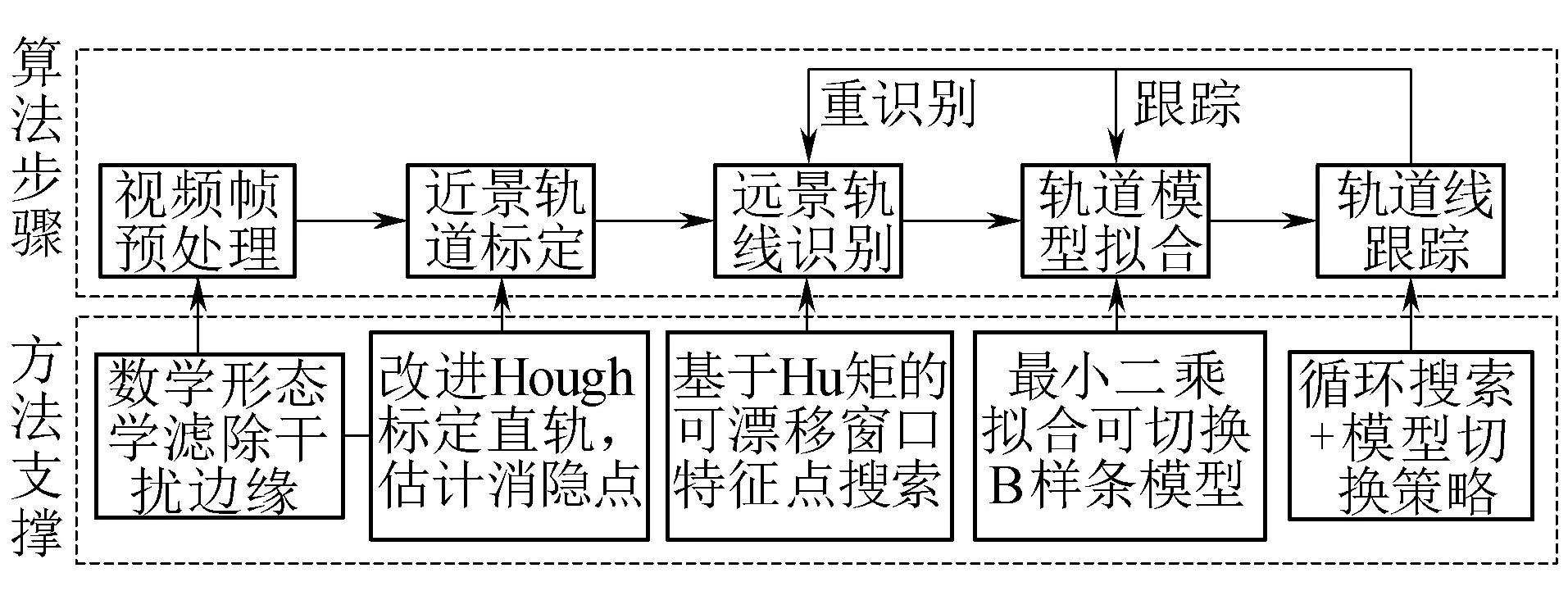
图1 铁路轨道识别算法架构
2 轨道边缘特征提取
2.1 图像预处理
钢轨所在环境背景中包含着复杂的纹理信息,同时车辆走行振动以及传感器处理环节使得轨道图像帧中产生噪声。本算法采用灰度直方图均衡法来降低光照变化的影响,通过中值滤波法减少非必要道砟纹理和噪声点。原图及处理结果如图2(a)、图2(b)示。

(a)轨道图像原图 (b)预处理

(c)Laplace算子 (d)Canny算子

(e)Sobel算子 (f)改进边缘检测结果图2 轨道边缘特征提取
2.2 轨道边缘特征提取与筛选
经车轮磨损后铁路钢轨面与轨枕和道床差异较大,其边界在灰度像素值上变化明显,可通过基于灰度梯度的边缘检测算子进行提取。通过实验发现:Laplace算子运算结果受纹理干扰较大,线性连续性不足;Canny运算符耗时较长,且得到了大量弱边界信息。而结构简单、实时性较高的Sobel算子,可有效提高算法的效率,摒除弱边缘信息干扰。实验结果如图2(c)、图2(d)、图2(e)所示。经标准Sobel算子提取得到的轨道线呈现双侧边缘,且其中仍然有来自轨枕的水平方向边缘信息、垂直方向边缘信息和部分杂散弱边缘。为减少干扰信息造成的误差,本文采用数学形态学来剔除干扰边缘。
数学形态学方法是根据构造得到的固定结构元素完成对数据的描述和处理,且对数据整体结构影响较小,具有较高的计算效率和准确度[12]。本算法的主要步骤为:通过分别建立垂直和水平方向的单线性结构元素来重构干扰信息,再在初步处理的边缘中剔除重构边缘以得到双线轨道,最后通过线间填充及形态学细化方法即可提取较为明确的钢轨脊线,检测结果如图2(f)所示。
3 基于B样条的可切换轨道模型
安装在机车上的视觉传感器与钢轨在图像空间中呈像具有视角固定的特性,采集的图像帧中轨道线呈现近景区直线轨道固定,远景区直曲线不断变化。本算法在近景区基于改进霍夫变换求解完成直线轨道标定,并固定直轨参数。直到视觉传感器位置变化,算法重新计算直轨数据,完成再次标定。轨道线识别的核心点在于完成对远景区轨道特征点的识别和模型拟合。
3.1 近远景区域标定
依据铁路线路标准对线路最小曲率半径和坡度的要求,钢轨表面可以认为是连续且平滑的[13]。依据视觉呈像原理,在世界坐标下平行的两条轨道线相交于投影图像内一点。此消隐点Pvanish(v,u)内方为轨道线范围。将轨道线范围以vb为界分割成远景区和近景区。视频帧的图像空间原点及方向定义如图3所示。

图3 轨道模型示意
3.2 分段可切换曲线模型
描述钢轨数学模型的选择需充分考虑拟合的精确性和算法的计算效率。经典的结构化路径检测拟合数学模型有多段直线[11]、高次曲线、贝兹曲线、双曲线[14]、样条曲线[15]等。因为B样条曲线具备描述精度高、修改灵活、线型光滑的优点。本文以B样条曲线作为远景区钢轨的数学模型。B样条曲线模型是由B样条基函数进行构造的。模型的数学描述为
(1)
式中:Pi为曲线控制点;n为曲线阶数;t为参量;Bi,n为样条基函数,n阶(n-1次)函数。Bi,n可描述为
(2)
为提高轨道线数学模型拟合的精度和抗干扰性能,本算法建立了以B样条为可动部分的分段可切换曲线模型。数学表达式为
C=[nPna] 1≤n≤3
(3)
式中:Pn为轨道线曲线模型的特征控制节点;n为曲线的阶数;a作为记录切换状态的符号。
当远景区钢轨呈现直线特征时,曲线可切换部分模型阶数取值为1,以远景区轨道线末端终点和分界点坐标实现模型描述。当远景区呈弯轨特征时,曲线模型可切换部分以3阶样条曲线进行拟合。数学表达式为:
(1)1次B样条直轨模型。模型取始终点坐标作为拟合的特征控制节点。
(4)
(2)3次B样条弯轨模型。曲线需由m+4个节点拟合确定,m为控制节点个数。通过设置三重坐标点方法确保曲线经过终点和始点坐标。
(5)
3.3 模型切换策略
设定近远景区模型切换的判断规则为:近景区固定直轨线斜率kp与边界点和曲线远景区特征终点所形成的斜率是否具有一致性。考虑像素偏差的影响,将判断条件表示为
(6)
当由算法搜索获得的特征点和双侧钢轨线的近远景边界点形成的斜率符合式(6)约束时,对切换记录标识a的值进行修改,采用3次曲线的模型完成拟合。
4 轨道识别与模型拟合
4.1 近景轨道位置标定
近景区轨道线标定即求解完成近景区直线模型的固定参量。直线提取常采用霍夫变换来完成,标准霍夫变换是将图像空间中的点映射为极坐标参数空间中的曲线,利用点线的对偶特性使直线的识别转化为统计过程[16]。算法具有较强的抗干扰优势,但以持续累加进行统计的方式较为耗时。
考虑在1 435 mm的标准轨道间距条件下,将视觉传感器固定于车辆后,通过试验确定呈像空间直轨的方向角范围为[65°,85°]和[-85°,-65°],且直轨线与图像空间原点距不大于图像的1/2对角线长。采用霍夫变换进行改进约束,提升累积效率。通过将算法中的统计单元(ρi,θi)分别在方向角范围内各取一个最大值实现。在像素为512×480的图像空间里,霍夫变换的算法结果如图4、图5所示。通过标准坐标与极坐标的变换关系ρ=vcosθ+usinθ,即可求解得到标准的直线参数为
(7)

图4 Hough变换图5 直线提取结果
由以上直线方程求解得到图像空间的左右线直轨延伸交点,即为消隐点Pvanish。本文算法通过视觉传感器的呈像模型及现场枕木施工间距将近远景区域边界点vb近似定于消隐点下1/2处。根据分区点的位置即可通过直线方程参数计算得到远景区的起始端点Pl0(vb,ul_boundry)和Pr0(vb,ur_boundry)。
4.2 基于Hu不变矩的轨道特征点提取
目前常用的以边缘方向和结构化特征为基础的轨道线检测识别方法难以处理因呈像所导致的仿射结果。Hu矩具备平移、旋转、尺度不变特性,本文通过基于Hu矩的可漂移检测窗口来满足特征点搜索需求。
4.2.1 Hu不变矩特征
常用的图像数据纹理特征分析度量算子有SURF、傅里叶描述子、不变矩等。Hu不变矩是由HU M K等提出的,大量试验证明了在笛卡尔坐标系下,由2、3阶归一化中心矩所构造的7个矩特征向量,不仅具有对灰度图像缩放及扭曲过程中所引起的变化特征描述值不变的特点[17],而且相对计算量更小。所以,本算法采用Hu矩作为轨道线搜索匹配的参数。
随机数据的分布可以用矩来描述。二维灰度密度函数同样可用以表示图像灰度值的分布情况。以矩作为灰度图像的描述时,尺寸为M×N像素的数字图像的p+q阶中心矩Mpq和几何矩upq可以表示为
(8)
(9)
式中:vp=Ml0/M00;uq=M01/M00;p,q值为0,1,…。通常,可以通过对中心矩实现归一化处理去除图像因缩放而产生的灰度变化。
(10)
式中:r=1+(p+q)/2,p+q=2,3,…。
针对Hu不变矩性能,通过各领域研究和实践发现其前4维的描述效果更突出[18],并可降低系统资源需求,提升计算效率。采用前4维特征量,其表达式为
(11)
鉴于Hu矩的处理结果数据范围较大,算法用对数表示结果,再参与比较。
Φi=abs(lgΦi)i=1,…,4
(12)
4.2.2 相似度度量
本算法中,欧几里得距离作为对照搜索窗内灰度特征与轨道线匹配程度的客观表征量,取特征值向量为Xk=[Φk1Φk2Φk3Φk4]。
(13)
式中:k为搜索匹配窗的标号;Dk为第k个搜索窗与前一搜索窗特征向量的欧式距离。
4.2.3 基于Hu不变矩的可漂移窗口搜索算法
常见的基于可漂移窗口的图像特征点检测算法通过设定等间距水平线来实现遍历搜索,算法在进行轨道线检测识别中的计算量较大,且包括大量非目标区域。本文根据轨道线延伸特性,提出一种以特征点转向偏移量为约束条件的移动窗口搜索方法。
为满足对于世界坐标下远景搜索区域的近似等间距划分,本文考虑道床枕木的等距施工特征,根据图像传感器的呈像原理,以枕木对远景区域的检测窗口实现尺寸设置和标定。标定方法为:以固定数目枕木敷设间距为间隔,标出检测范围内的分界线LImage_i。通过度量相邻分区的间隔距离比例来确定下一分区位置,记分界线为l1,l2,l3,…。各分区宽度设置为ai=0.5LImage_i,在近远景边界点(vb,ul_boundry)和(vb,ur_boundry)分别设置搜索窗wli、wri,依据下文步骤展开搜索。搜索算法示意图如图6所示。

图6 特征点搜索方法示意
以轨道线搜索窗的选择为依据,轨道线模型控制点的提取步骤如下:
步骤1由Pl0、Pr0检测窗数据计算得到特征匹配窗内对象的Hu矩Xl0=[Фl1Фl2Фl3Фl4],Xr0=[Фr1Фr2Фr3Фr4]。
步骤2以分步定位为原则,设置分区边界l1上的wl1、wr1,由(ul0+ur0)/2开始检测,检测步长为ai/2,向两侧于[vl0,vr0]中记录矩距离的极小值Dmin;初步定位后,通过遍历步长范围内的点求取欧式距离最小值。
步骤3远景区曲线轨道的弯曲方向由计算Pl0,Pr0和Pl1,Pr1在水平方向的偏移量Δd得到,并设误差范围e。
步骤4将相隔连续已确定控制点的正向延长线与下一分界线的交点作为起点。若Δd>e,则单向检测,正则向右,负则向左。若Δd≤e,取双侧进行搜索。
步骤5取匹配度度量值T,Dmin≤T时,记录此处轨道线特征点坐标值作为控制点;Dmin>T而搜索未结束时,以获得的前2个特征点坐标为依据,采用其向远景延长线方向的搜索起点作为特征点,将始点进行dl或dr距离的偏移,作为此分区的控制点坐标。
步骤6判断算法是否终止,否则继续下一检测位置搜索,转步骤4。终止条件:
(1)下一次搜索窗坐标超出消隐边界;
(2)两侧轨道线搜索获得的控制点位置坐标距d=uri-uli小于设定的阈值,即认定轨道线近似相交。
步骤7进入模型判别,拟合模型参数。
4.2.4 模型拟合
通过漂移窗检测得到的控制起始点坐标进行可切换模型确定,以最小二乘法实现对选定模型的拟合及求解。本文举例视频帧中采集的左轨线特征点及其Hu不变矩值见表1。模型拟合匹配结果如图7所示。

表1 示例中的轨道线特征节点提取数据

图7 轨道模型拟合匹配结果
5 轨道模型识别及更新算法流程
本文所提钢轨检测提取算法流程主要分为初始化处理、近景区直轨线固定参数求解、远景区曲线拟合与跟踪3部分,检测流程如图8所示。在轨道线检测中算法受环境及噪声干扰而出现异常或识别不出轨道线信息时,算法通过判断终止条件在给出识别错误的同时重新开始进行处理。在正常情况下,算法自动完成对于轨道线的参数更新。
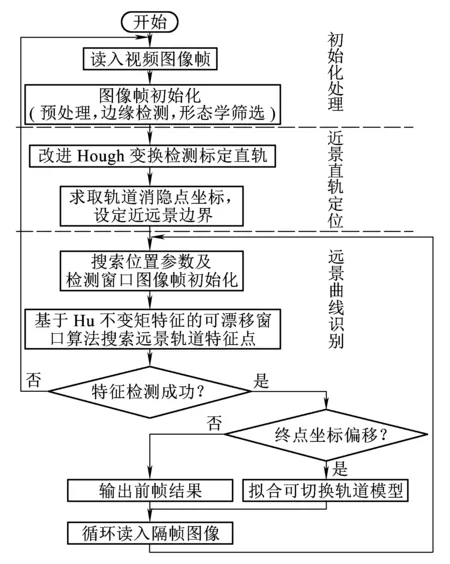
图8 轨道检测算法流程
更新及追踪过程考虑到图像传感器隔帧采集到的轨道线变化情况较小,呈像线路参数一致性较高,本文算法通过设置隔帧采集并优先针对上次控制终点进行搜索匹配。若搜索的结果与上次终点坐标一致,则以上帧结果为输出,若出现偏移,则根据算法流程进行线路模型的重新拟合跟踪。
6 结果分析与验证
本算法通过Matlab2013编程实现,实验检测所用计算机系统为Windows7,系统CPU为2.4 GHz的Inter CORETMi3处理器。
6.1 算法准确性对比分析
采用与人工标定结果进行对比,以左右轨道线拟合函数值与标定曲线差值的平均值作为误差度量值,复现了文献[8]中算法作为参照。以图2轨道为例,误差统计如图9所示。在远景区域内,文献[8]算法不具备适应性,本文算法拟合误差较小;在近景区域内,本文算法准确度更优。

图9 轨道检测误差统计
6.2 算法鲁棒性和实时性分析
实验图像数据包括246幅钢轨的灰度图片和120帧列车驾驶室的视频序列帧。图像像素尺寸为256×240。实验对比结果见表2。本文算法实现对钢轨的识别平均需要时长为81 ms,完成对钢轨特征点提取及模型重拟合的时长为172 ms,识别正确率可达88.93%;文献[8]算法轨道线提取时间均值为316 ms,正确率为55.74%,且文献[8]算法难以准确识别远景区曲线钢轨。较为典型的场景下钢轨的识别结果如图10所示,其中本文方法如左侧所示,文献[8]算法如右侧所示。

表2 算法实验结果对比
图10(a)为光照充足无砟道床场景下的轨道图像,本文算法能够提取钢轨脊线位置,而文献[8]算法识别到的轨道线产生了偏移。图10(b)为阴雨天较差可视环境下小弯轨轨道图像,本文算法可有效检测出前方弯轨。图10(c)为存在强干扰场景下的弯轨轨道,本文方法因光影信息使匹配结果出现偏移,文献[8]算法仅准确识别到右轨道线信息,左轨受强边缘干扰及弯轨曲率而产生误检。图10(d)中出现的单边遮挡物使本文算法在右侧远景区域轨道边缘检测未能准确匹配,而文献[8]算法因前方轨道斜率变化仅匹配到部分近景轨道。由此可以看出,本文方法对于场景变化的鲁棒特性更好,同时数学模型能更精确地拟合轨道线。

(a)光照充足无砟道床直轨图像

(b)阴雨天有砟弯轨轨道图像

(c)有阴影干扰弯轨轨道图像

(d)有遮挡干扰直轨轨道图像图10 轨道线检测实验结果
7 结束语
本文依据机器视觉在提取轨道线过程中的特性,提出一种分段可切换的曲线模型来实现轨道线的描述。其中,通过数学形态学方法能在初始化处理阶段较好地消除边缘中的干扰信息。在检测跟踪过程中,基于改进霍夫变换能求解得到近景区直轨参量;通过以Hu矩来度量匹配度的可漂移窗口搜索算法能完成对于远景区钢轨特征点的识别,基于模型更新步骤及规则来完成可切换样条模型拟合过程。在多种环境场景下的实验表明,算法可以有效应对图像中轨道线的仿射变化,具备一定的实时性和鲁棒性。后续工作开展中,可将算法融合进路轨前方障碍物探测、铁路视频监控等技术领域,以期实现工程应用。

