考虑天气状态的接触网可靠性评估方法研究
王 贞,林 圣,冯 玎,高仕斌,陈 静
(1.西南交通大学 电气工程学院,四川 成都 610031;2.国网山东省电力公司 莱芜供电公司,山东 莱芜 271100;3.中铁第一勘察设计院集团有限公司,陕西 西安 710043)
高速铁路牵引供电系统要求具有极高的运行可靠性[1-3],无备用接触网系统是牵引供电系统的关键组成部分,其能否安全可靠地进行服役直接关系到机车的安全、稳定运营。因此,如何更加准确评估接触网的可靠性并使之提高,成为提高整个高速铁路可靠性的关键[4]。
接触网系统由完全暴露于室外的元件组成,受外部天气因素影响较大,其故障率与修复率具有随机模糊的特性,不是恒定常数。但目前对于接触网的可靠性评估基本都是基于元件恒定故障率来进行的,如文献[5-7]在假定故障率与修复率为恒定常数的特殊条件下分别基于马尔科夫、贝叶斯网络以及GO-FLOW方法建立接触网可靠性分析模型,对接触网系统的可靠性进行评估。
目前,国内外对考虑接触网可靠性受天气影响的研究鲜有报道,但针对输配电系统可靠性受天气状态影响的研究相对较多。文献[8]在配电网可靠性评估中,提出了恶劣天气严重程度和持续时间概率特性对故障率和修复时间影响的模型。文献[9]给出了基于天气因素的可靠性参数修正模型,计算结果验证了天气因素对配电网可靠性指标有较大影响。在此基础上,文献[10]利用联系数理论处理故障率与天气波动,提出了考虑天气变化的输电系统可靠性评估方法。以上研究在一定程度上考虑了天气对可靠性参数或指标的影响,但未充分考虑故障率、修复率及天气状态的随机模糊性。
文献[11-12]运用可信性理论有效地解决了电力系统中数据的随机模糊性问题,并在电力系统风险评估、电网规划等方面得到了较好地应用。基于此,文献[13]基于可信性理论对接触网系统可靠性进行模糊评估,文中并没有考虑天气状态对系统可靠性指标的影响。但在我国电气化铁路中,如兰新线、武广线等接触网系统受大风、雷雨等恶劣天气情况的影响较严重,其子系统元件故障率、修复率的随机模糊性明显。因此,在进行接触网可靠性评估时有必要考虑天气状态对其评估结果的影响。
针对上述问题,本文提出一种考虑天气状态的高速铁路接触网系统可靠性评估方法,此方法依据IEEE标准导则[14]将天气分为正常(Normal)天气、恶劣(Adverse)天气、灾难(Storm Disaster)天气,建立三态天气可靠性评估数学模型,将周期内统计所得各类元件平均故障率、修复率以及各天气状态持续时间所占统计周期的比例作为原始参数,通过三态天气模型求取不同天气状态下元件故障率、修复率,由于元件故障率、修复率以及天气状况均具有不确定性,故将其看作随机模糊变量,运用可信性理论处理故障率、修复率以及天气情况变化。通过GO法计算不同天气状态下接触网系统可靠性指标。此方法能够在原有数据基础上得到不同天气状态下系统可靠性指标,减少了数据统计量,同时保留了原始数据的随机模糊性,贴近现场实际。
1 考虑天气状态的元件参数模型
接触网系统的全部设备均在户外运行,特别是接触线,受天气的影响比较大,不同天气状态下元件故障率与修复率不同。灾难天气状态下,大暴雨、暴雨等容易造成绝缘子的闪络,暴风容易将接触线、吊弦、承力索等吹断,同时容易将异物吹到接触网上导致短路跳闸,暴雪低温容易使接触线敷冰导致受电弓不能正常取流;恶劣天气下,雷击导致过电压引起绝缘子损坏,同时过电压侵入变电所导致跳闸[15];正常天气下,鸟害鸟窝、施工等意外情况是引起接触网故障的主要因素。不同天气状态下元件的故障率存在较大差异,灾难天气下元件发生故障的可能性明显增加[16]。同时受工作环境的影响,灾难天气及恶劣天气下设备修复率会低于统计周期内的平均修复率。为此本文建立三态天气下元件的故障率及修复率修正模型,定量表征天气状态对接触网故障率及修复率的影响。
1.1 三态天气下元件故障率修复模型
将天气分为正常(Normal)天气、恶劣(Adverse)天气、灾难(Storm Disaster)天气3个状态,三态天气的持续时间都是随机的,采用期望值来描述。在一个统计周期内,三态天气持续时间期望值与元件故障率关系如图1所示。S表示灾难天气持续时间期望值,D表示恶劣天气持续时间期望值,N表示正常天气持续时间期望值,T表示统计周期。对应天气状态下故障率分别为λs、λd、λn。

图1 统计周期内三态天气持续时间期望值
设某类元件平均故障率为λavg,在第j态天气下元件故障率为λj,统计周期为T,元件在统计周期内发生故障的总次数为Nλ,第j态天气持续时间期望值为Tj,第j态天气下发生故障次数为Nj,则有
(1)
设Pj为第j态天气持续时间占统计周期的百分比,则有
(2)
由式(1)、式(2)可得
λavg=∑Pjλjj=s,d,n
(3)
式(3)即为三状态天气模型下各类元件故障率的修正模型[8]。
设Fj表示某类元件在第j态天气下发生故障次数占统计周期内总故障次数的百分比,则有
(4)
如何求得第j态天气某元件故障率λj是评估接触网系统不同天气状态下可靠性指标的关键,但现场实际中λj较难得到,而λavg的值相对容易统计,若知道某类元件在第j态天气下发生的故障次数占统计周期内总故障次数的百分比Fj,则由式(3)、式(4)可推导出
(5)
对于某类元件在第j态天气下发生故障次数占统计周期内总故障次数的百分比Fj是一个相对稳定值,通过多年统计结果可以将Fj看作是已知量,故只要统计得到第j态天气持续时间占统计周期的百分比Pj,运用式(5)即可在统计所得各类元件平均故障率的基础上求得三态天气下各类元件的故障率。
1.2 三态天气下元件修复率修正模型
平均修复时间是指可修复元件的平均修理时间,其估计值为修复时间总和与修复次数之比,在可修复系统中,平均修复时间倒数即为修复率[17]。设某类元件统计周期内平均修复时间为Tavg,灾难天气、恶劣天气、正常天气状态下平均修复时间为ψs、ψd、ψn,对应的故障次数为Ns、Nd、Nn,则有
j=s,d,n
(6)
在现场实际中,3种天气状态下的平均修复时间也较难获得,而Tavg的值却较容易统计,因而同样只要知道3种天气状态下某类元件平均修复时间的比值即可通过式(6)计算得到各类元件不同天气状态下的平均修复时间,从而求得修复率为
μj=1/ψjj=s,d,n
(7)
3种天气状态下某类元件平均修复时间的比值是一个相对稳定的值,通过多年的统计结果可以将其看作已知量,进而可在统计所得周期内各类元件平均修复时间基础上通过式(6)、式(7)求得不同天气状态下某类元件修复率。
在上述公式中,λavg、Tavg、Pj、Fj的求取通常是用几个日历年统计结果的平均值,现场实际中,这些参数因统计误差或者统计资料不足而具有不确定性。为了考虑这些不确定性因素对系统可靠性评估的影响,本文基于可信性理论进行不确定性建模。
2 基于可信性理论的不确定性建模
可信性理论将模糊论与概率论在测度的基础上有机结合,适用于具有随机性与模糊性系统的综合评估,为随机模糊双重不确定性问题的求解工作提供了可能[18]。接触网各类元件故障率、修复率以及天气状态具有模糊性与随机性的特性,可信性理论能够有效处理该特性。本文将三态天气模型下所求故障率与修复率看作随机模糊变量,满足了其随机性和模糊性的双重特性,同时也反映出天气状态的不确定性,进而运用可信性理论求得接触网系统不同天气状态下的可靠性指标。
具体做法是通过式(5)~式(7)计算得到某类元件在第j态天气下的故障率λj、修复率μj,将计算所得λj、μj视为随机模糊变量ξ、η,接触网系统的可靠性指标计算转换为运用可信性理论求解随机模糊变量数学期望值的数学问题。下面给出与本文相关的几个概念与计算式。
假设Θ为非空集合,P(Θ)为Θ的幂集,若Pos满足可信性理论的四条公理[19],则称Pos为可能性测度;(Θ,P(Θ),Pos)则为可能性空间;A为P(Θ)中的一个集合,Ac为A的对立集合,则Nec{A}=1-Pos{Ac}为A的必要性测度;Cr{A}=(Pos{A}+Nec{A})/2为A的可信性测度。
可信性测度与隶属度函数之间有如下关系,对于隶属度为g的模糊变量ξ,设B为P(Θ)中的集合,Bc为B的对立集合,有
(8)
如果随机模糊变量ξ、η是从可能性空间(Θ,P(Θ),Pos)到随机变量集合上的映射,则函数f关于变量ξ、η的期望值为
Epro-fuz[f(ξ,η)]=

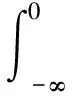
(9)
其中
Epro[f(ξ(θ),η(θ))]=

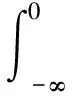
(10)

在处理系统的一般随机模糊变量时,很难直接通过上式求得所需要结果,为此本文通过随机模拟技术求取期望值,当N充分大时,对任意的r≥0,可信性测度Cr{θ∈Θ|Epro[f(ξ(θ),η(θ))]≥r}可近似为
Cr{θ∈Θ|Epro[f(ξ(θ),η(θ))]≥r}≈
(11)
对任意的r<0可信性测度Cr{θ∈Θ|Epro[f(ξ(θ),η(θ))] Cr{θ∈Θ|Epro[f(ξ(θ),η(θ))] (12) 其中,Epro[f(ξ(θk),η(θk))]可以通过随机模糊模拟得到,则式(9)可由式(11)、式(12)两式等价求得,随机模糊变量的期望值Epro-fuz[f(ξ,η)]即可求得。 在系统可靠性和风险评估分析中,故障树分析法是比较常用的一种方法,而GO法是另一种以成功为导向的系统可靠性分析方法,相比于故障树有其自身特点[20]:一是GO法以成功为导向选择相应的GO操作符直接将系统原理图转换为模型图,GO图中的操作符与系统中部件一一对应,能够清晰地反映系统结构组成,明显描述出相关部件之间的关系及相互作用,易于与原系统进行核对;二是通过GO运算计算元件各种状态发生的概率,不需要最小割集,直接对系统定量分析,求解精度高。综合分析,GO法能够将接触网系统失效模型直接转换为GO图进行可靠性评估,模型结构清晰,贴近现场实际,以信号流为成功导向计算简单明了,因此本文选择GO方法计算不同天气状态下系统可靠性指标。 只有当所有部件都正常工作时接触网系统才能正常工作,接触网系统失效时,可以等效看作是接触线、承力索、绝缘子、吊弦、承力索座、水平拉杆、定位装置、套管、线夹、定位环、斜腕臂、支柱基础等失效部件的串联系统,为分析方便,假设各类元件为一个单元。本文根据接触网系统等效失效模型,以系统能正常工作为成功导向,依照GO法模型与逻辑框图一一对应原则建立接触网系统GO图,为保证GO图完整性,以操作符5(信号发生器)代替外部供电系统作为输入信号,接触网元件采用操作符1(两状态单元)代替,系统失效模型及GO图如图2所示。图2中“5-0”指操作符为5,元件标号为0,输出信号流“12”的输出数据代表接触网系统的可靠性指标。本文只针对接触网系统进行可靠性评估,故假设操作符5的失效概率为0。 在图2中给定各单元可靠性参数,即可根据GO运算计算出整个系统可靠性指标。实际工程中一般给出元件故障率和修复率两个参数,据此可以计算输出信号的故障率与修复率,进而可计算出整个系统的可用率。 (a)接触网系统等效失效模型 (b)接触网系统GO图图2 接触网系统失效模型及GO图 接触网系统是一个具有停工相关的串联可修复系统,即系统因某单元故障而停工时,没有故障的单元随系统停工而停止运行,且不再发生故障,直到系统修复,这些单元再恢复正常运行[21]。考虑到接触网系统实际工况,认为整个系统各单元之间均存在停工相关且停工阶数I=1。此时对于两状态单元,输出信号计算公式为 (13) 式中:λC、μC为操作符本身故障率与修复率;λS、μS为输入信号故障率与修复率;λR、μR为输出信号故障率与修复率。 当多个单元存在一阶停工相关时,串联结构故障模式只是1个单元故障,没有2个或者多个单元同时故障,由式(13)得串联结构等效故障率为所有单元故障率之和;系统故障率和修复率比值,是所有单元故障率和修复率的比值之和[21],将故障率与修复率看作随机模糊变量,得到三态天气下系统等效的故障率、修复率、可用率、平均故障时间间隔公式为 (14) (15) (16) (17) 运用式(5)~式(7)计算求得不同天气状态下各单元故障率、修复率,通过式(14)~式(17)将接触网系统可靠性评估问题转换为随机模糊变量数学期望求解问题,即可运用可信性理论实现接触网系统的可靠性评估。由于算法求解过程用到随机模糊模拟的方法,因此求解结果存在一定随机性,重复求解M次,分析结果分布规律,给出置信区间,具体算法流程如图3所示,图3中N指随机产生N个r,算例中M、N均取1 000。 图3 三态天气下可靠性指标计算流程 本文采用文献[13]宝成铁路的统计数据,以100 km长的接触网为统计基准,对每个部件的失效和维修情况进行记录,得到各部件不考虑天气状态时元件的平均故障率与修复率,见表1,以此为原始数据。假设通过对几个日历年的数据分析得出正常天气、恶劣天气、灾难天气持续时间占统计周期百分比均值Pj分别为90%、9.9%、0.1%,假设故障发生在正常天气、恶劣天气、灾难天气下的次数占总故障次数的百分比Fj分别为50%、45%、5%[8],并且假设在正常天气、恶劣天气、灾难天气时元件的修复率之比为6∶5∶4。 表1 接触网各元件故障率与修复率 基于可信性理论,随机模糊变量的模糊性可以用各种形式的模糊定义来表达,通常所用表示形式有三角形模糊数及梯形模糊数。本文为研究模糊数表示形式对可靠性计算结果的影响,以系统故障率为例,分别用三角形模糊数以及梯形模糊数来描述各元件故障率的模糊分布,以表1中故障率的±2%误差作为模糊分布上下限,0.2%误差作为可能性最大值,通过图3所示流程图以及式(14)计算系统故障率,重复计算1 000次,对计算结果拟合求得95%置信区间及均值,见表2。 表2 不同模糊变量表示形式下系统的故障率 a-1 由表2可知,用三角形模糊数表示各元件故障率时求得系统故障率均值为2.493 0 a-1,用梯形模糊数表示各元件故障率时求得系统故障率均值为2.491 9 a-1。表明不同模糊表示形式对所求系统可靠性指标结果几乎没有影响,本文在后文算例中选择三角形模糊数来表示各元件的故障率与修复率。 在实际计算中模糊区间难以给出具体定义,为研究模糊区间范围对可靠性结果的影响,以求取系统故障率为例,用三角形模糊数表示表1中各元件故障率,以故障率的±α误差作为模糊分布上下限,0.2%误差作为可能性最大值,选取不同的α值,通过图3所示流程图以及式(14)计算α值不同时系统的故障率,计算结果如图4所示。 图4 不同模糊区间范围的计算结果 由图4可知,不同模糊区间上下限对计算结果有一定影响,区间范围越大,计算结果越小。因而,为考虑线路实际服役环境的天气变化情况,计算时可将统计周期内几个日历年中λavg、μavg的最大值作为模糊区间上限,最小值作为下限,均值作为可能性最大值。由于本文统计数据有限,故在后文计算中选择故障率与修复率的±2%误差作为模糊区间上下限,0.2%误差作为可能性最大值。 运用式(5)~式(7)及表1数据,计算得到不同天气状态下各元件的故障率与修复率,见表3。 表3 三态天气下各元件的故障率与修复率 将计算所得三态天气下接触网系统各元件的故障率以及修复率均视为随机模糊变量,以±2%误差作为模糊分布上下限,0.2%误差作为可能性最大值,通过图3所示流程及式(14)~式(17)可得接触网系统三态天气下可靠性指标的评估结果。由于在计算过程中用到了随机模拟算法,重复计算1 000次,对不同天气状态下接触网系统可靠性指标计算结果进行拟合,系统可用率拟合结果如图5所示。图5中横坐标表示系统可用率,原始数据指经过1 000次计算得到的系统可用率样本,拟合结果属于正态分布。 (a)不考虑天气时系统可用率 (b)正常天气时系统可用率 (c)恶劣天气时系统可用率 (d)灾难天气时系统可用率图5 系统可用率拟合结果 通过拟合结果服从正态分布求得各可靠性指标95%置信区间及均值,见表4。 表4 接触网系统三状态天气下可靠性指标计算结果 比较表4中三状态天气下接触网系统平均故障时间间隔可知,不考虑天气状态时接触网系统平均故障时间间隔为0.401 1 a,灾难天气时系统平均故障时间间隔均值为0.008 025 a,恶劣天气时系统平均故障时间间隔值为0.088 25 a,正常天气时系统平均故障时间间隔为0.722 0 a,显然不考虑天气时系统平均故障时间间隔与灾难天气时系统平均故障时间间隔相差较大,系统修复率与故障率以及可用率也存在类似规律,故在对接触网系统进行可靠性评估时考虑天气状态十分必要。 本文以高速铁路接触网系统为研究对象,建立三态天气下可靠性评估模型,并运用可信性理论求解不同天气状态下系统可靠性指标,以宝成铁路长年统计数据进行算例分析,对该方法实用性进行验证,得出如下结论: (1)不同天气状态下可靠性指标存在较大差异,在接触网可靠性评估中,分别求取不同天气状态下可靠性指标十分必要。该方法只需统计周期内平均故障率与修复率以及不同天气状态持续时间占统计周期百分比即可求取不同天气状态下接触网系统可靠性指标,能够克服现场难以得到不同天气状态下元件故障率、修复率的问题,减少现场数据统计工作量。 (2)将不同天气状态下故障率与修复率看作一个随机模糊变量能够直观地反映其模糊性与随机性,不同模糊区间上下限对计算结果有一定影响,计算时可将统计周期内几个日历年中λavg、μavg的最大值作为模糊区间上限,最小值作为下限,均值作为可能性最大值,从而保证数据完整性,贴近现场实际情况,这对我国运行时间短,缺少实际统计数据的高速铁路可靠性评估有一定实用价值。3 考虑天气状态接触网可靠性评估
3.1 接触网系统GO图的建立


3.2 三态天气下系统可靠性指标计算


4 算例分析

4.1 模糊变量表示形式对计算结果的影响

4.2 模糊区间范围对计算结果的影响

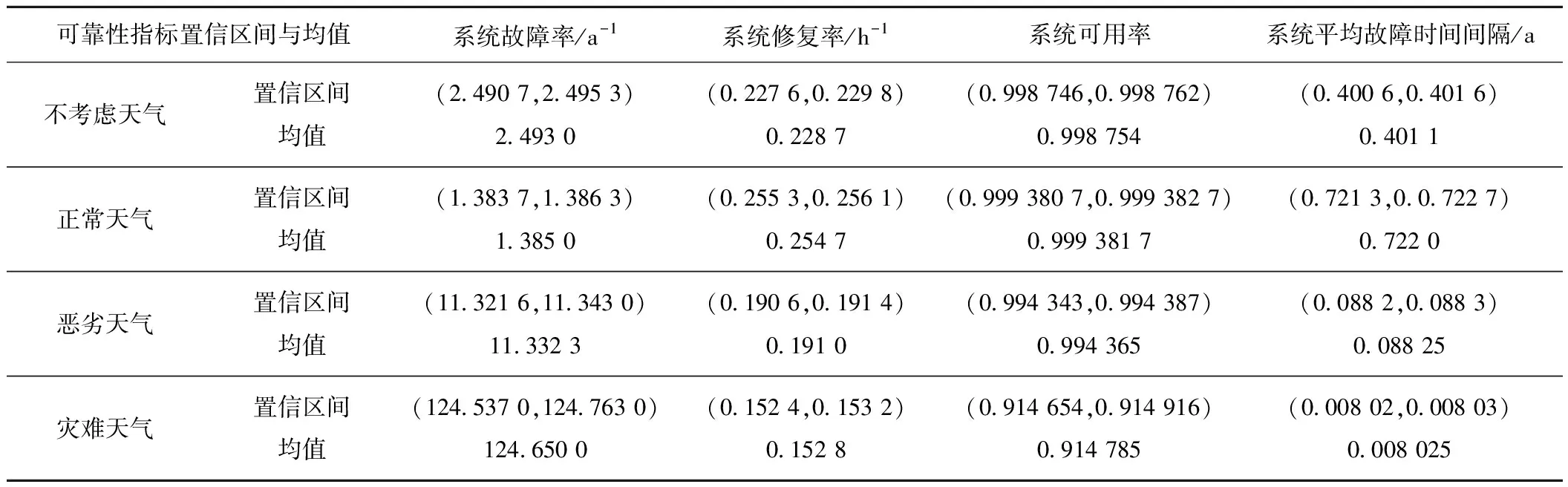
4.3 三态天气下系统的可靠性指标计算
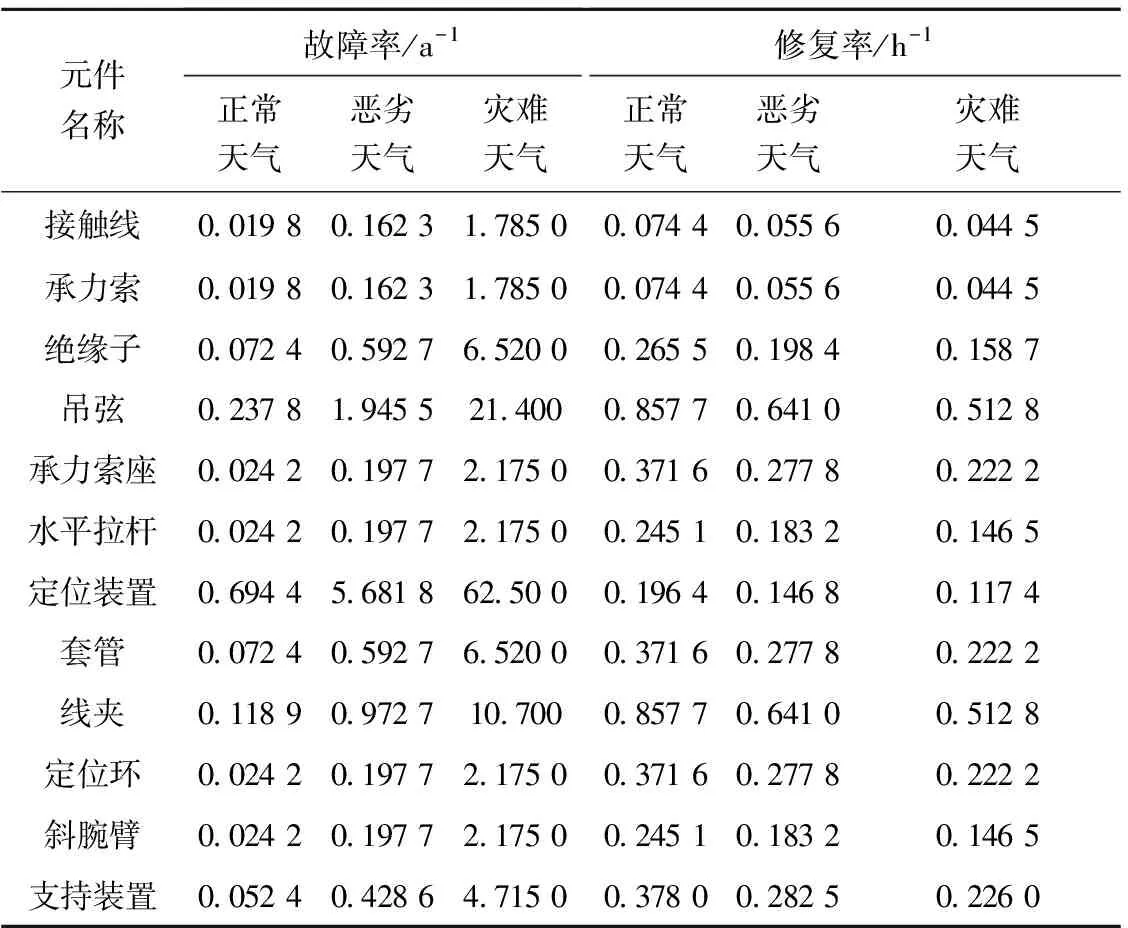

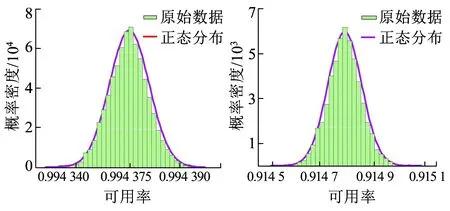
5 结论

