基于分数阶PID控制器的地铁列车优化控制研究
张 驰,谭南林,周 挺,刘敏杰,单 辉
(1.北京交通大学 机械与电子控制工程学院,北京 100044;2.常州市轨道交通发展有限公司,江苏 常州 213022)
地铁列车作为轨道交通的重要通行方式,运输能力大、运行速度快,承担了大部分的乘客运输任务。随着我国城市化建设的快速发展,对其运力也提出了更高的要求。列车自动驾驶ATO系统利用车载固化信息和地面通信实现对列车牵引、制动的控制,可使列车处于更佳的运行状态,提供更优的区间运行模式,提高旅客舒适度、行车密度和准点率。列车控制算法是ATO系统的核心技术, 深入研究此项技术对我国开发具有自主知识产权的城市轨道交通列车控制系统具有重要意义。
目前,针对ATO系统的研究主要集中在列车运动模型建模和响应追踪控制器两个方面。在列车运动模型建模上,文献[1]根据动力学原理建立模型,但这种模型忽略了控制力产生的动态过程。文献[2]提出了面向控制的列车制动模型。文献[3-6]以此模型为基础进行自动驾驶、精确停车和ATP限速下ATO控制算法研究,但未考虑到列车牵引制动特性,使模型在列车高速状态下误差增大。为此,本文以该模型为基础,进一步引入列车牵引制动特性以降低误差。
另外,地铁列车在运行时受到的阻力负载随着线路的情况、运营的情况和车辆的工况而变化。文献[2]中的模型未定义基本阻力,影响了模型的精度。针对该问题,列车模型参数识别大多采用最小二乘法。如文献[7-8]应用最小二乘法获得磁悬浮列车对应模型参数。最小二乘法可以快速收敛到真值,但对有色噪声会产生偏差。文献[9]采用极大似然法对高速列车的非线性模型参数进行识别,而极大似然法可能存在局部收敛,且需要先验知识。
在响应控制器方面,出现了多种不同的控制方法。文献[10]中的PID控制算法具有良好的控制精度,但是不能兼顾系统响应的快速性和稳定性。文献[11]中的模糊控制具有较好的鲁棒性和快速性,但控制精度不高,且控制参数和控制规则的调整耗时耗力,不利于工程中的实施。文献[12]中的神经网络控制算法复杂,缺乏实时性。
近年来,分数阶微积分理论和应用研究成为热点研究课题,它不仅是很好的建模工具,而且还可以从数学上精确证明系统的正确性。文献[13]提出分数阶PIλDμ控制器,并比较了分数阶PIλDμ与传统整数阶PID控制器在控制分数阶系统和整数阶系统时的性能差别,体现了分数阶控制器的潜在优势。文献[14-15]讨论了分数阶PIλDμ控制器在运动控制中的应用,通过积分误差寻优的方法设定分数阶PIλDμ控制器的参数。文献[16]对分数阶PIλDμ型控制器的应用进行了深入研究,使分数阶PIλDμ型控制器在工程领域可以得到很好的应用。对于实际情况中的受控对象,文献[17]提出可以根据期望的幅值裕量Am和相位裕量φm来设计分数阶PIλDμ控制器。文献[18]基于Routh-Hurwitz稳定性判据,研究了分数阶混沌系统在平衡点处的反馈控制问题。并且分数阶PIλDμ在文献[19]中应用到智能车控制,在文献[20]应用到导弹控制。
本文以地铁列车为研究对象,建立更为完善的列车运动模型,从实际数据中用遗传算法校准得出列车的基本阻力参数。针对目标曲线跟踪控制问题,依据分数阶PIλDμ控制算法对列车ATO建立了一套更加优化的自动驾驶控制算法。通过系统仿真以及与实际列车的运行数据进行比较,结果表明该算法能够使ATO系统达到更优的速度控制效果。
1 优化列车运动模型
1.1 列车运动模型
在地铁工程设计中,把运行中的列车看作是全部质量集中于重心的平移运动和某些部分进行回转运动(车轮、电机)的刚体运动。地铁列车的运动由ATO系统通过牵引制动系统实现控制,但ATO系统不能直接操纵列车动力执行机构,如电机、内燃机等。因此,构建列车运动模型时必须考虑传输延时和响应时间。
参照文献[2]中的列车运动模型,如图1所示。

图1 列车运动模型

A(t)=F(u(t))=f×u(t)+e
(1)
式中:f和e为F(·)的系数。
然而,值得注意的是,A(t)和u(t)两者之间并不是理想的线性关系,现有模型没有考虑列车在不同速度及不同工况下牵引制动能力的非线性特征。牵引和制动特性曲线的确定受到以下条件的限制:车重和黏着系数,最大线路功率和电机颠覆转矩。以南京地铁一号线A型列车为例,载客质量及列车质量见表1,表1中定员载荷为6人/m2,超载为9人/m2,乘客每人质量按60 kg计算,上述参数依照《地铁车辆通用技术条件》进行设定。
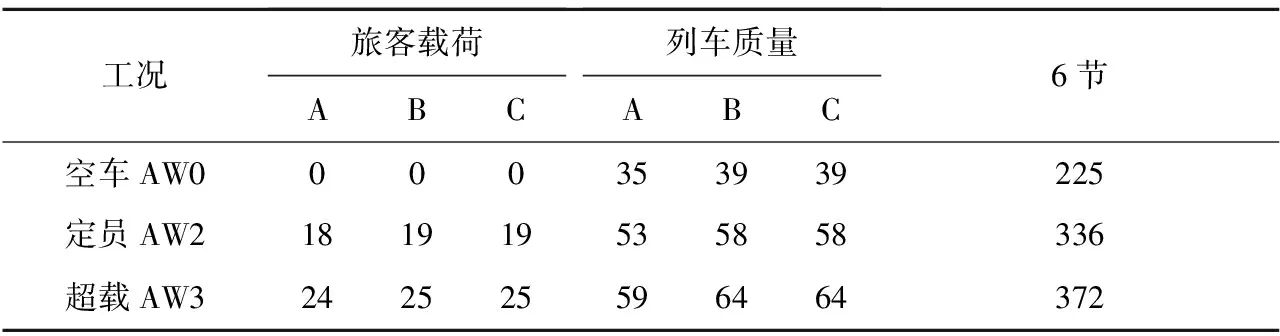
表1 载客质量及列车质量 t
各工况的列车牵引特性曲线和制动特性曲线如图2、图3所示。
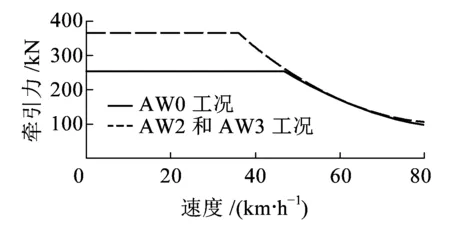
图2 列车牵引特性曲线

图3 列车制动特性曲线
从列车牵引特性曲线和列车制动特性曲线可以看出,大部分情况下,两者都是在低速区间为常数值,高速区间有所降低。为了简化计算,将列车牵引特性和列车制动特性都设定为分段函数,并根据曲线特征分别简化成一次或者二次函数。在AW0工况下牵引力为
F(v)=
(2)
在AW2和AW3工况下牵引力为
F(v)=
(3)
在AW0工况下制动力为
F(v)=264 kN
(4)
在AW2和AW3工况下制动力为

(5)
1.2 列车基本阻力辨识
列车基本阻力计算是列车牵引计算中的一个重要组成部分,其计算结果的合理性、准确性对列车的运动学仿真具有重要意义。从实际线路中得到的基本阻力系数信息,对建立运行时间模型、能耗模型有很大的帮助。
列车在实际运行过程中所受到的阻力可以分为基本阻力和附加阻力。列车运行时影响基本阻力的因素极为复杂,包括轴承类型、润滑油性质、轮对转速、车轮半径和车轮踏面形状等。因此,通常使用大量实验综合出经验公式进行计算。参照戴维斯公式,单位基本阻力ω0(N/kN)等于列车运行速度的一元二次方程,即
ω0=a+bv+cv2
(6)
式(6)中的系数a、b、c需要辨识。系数的值对某一列车是确定的,但是随着机车运营年限的增加,列车的机械阻力和气动阻力会发生改变,列车轮对与轨道的摩擦所形成的阻力也会发生变化。如果此时基本阻力运算的系数还使用初始设定的经验常数,对于模型的仿真计算将会引起较大误差。
针对这一状况及需求,本文采用现场采集的实际运行数据对基本阻力系数进行辨识。由于获取的数据量不足,不适用训练学习的算法进行辨识。考虑到虽然现有车载记录仪可以获得地铁列车实际运行过程中的牵引力、制动力、速度等数据,但是精度不高,速度只能精确到千米每小时,行程只能精确到米。若采用最小二乘法算法进行参数辨识会出现过拟合现象,易受噪声影响,放大误差。因此,本文选用遗传算法对阻力参数进行辨识。
遗传算法具有计算时间少、鲁棒性高、收敛性好等优点。时间乘以误差绝对值积分(ITAE)的性能指标是具有很好工程实用性和选择性的控制系统性能评价指标。对基本阻力参数辨识应用遗传算法时,个体的适应度是记录仪采集到的速度值v(t)和距离值s(t)两者的ITAE性能指标的乘积,并对一定误差范围之内的值进行剔除,以减少采集精度对结果的影响。选取的适应度函数为

(7)
2 基本阻力系数及分数阶PIλDμ算法
分数阶PID控制器引入了积分阶次λ和微分阶次μ两个可调参数,从而使得控制器参数的整定范围变大,控制器能够更灵活地控制受控对象,可以期望得到更好的控制效果。由文献[13]提出的传递函数为
(8)
本文参照的分数阶微积分Riemann Liouville(RL)定义为
(9)

分数阶PIλDμ型控制器具有对被控系统的参数变化不敏感的特点。本文采用的列车运动模型加入了列车牵引制动特性这一非线性特征,且列车运动本身还具有时滞性、非线性的特点,所以传统方法并不能准确反映列车的动力学特性,而适用于分数阶PIλDμ型控制器来进行控制。分数阶PIλDμ型控制器对非线性控制对象有很强的抑制力,可以较好地实现对非线性环节的控制。通过调整比例系数、积分系数、微分系数、积分阶次和微分阶次这5个参数,可以使系统得到更加快速精确的控制效果,取得比常规控制器更优的动态性能和鲁棒性。在对分数阶微积分的实际应用中,由于计算量大,限制了此算法的应用,所以,基于Oustaloup算法这一数字实现,在幅频特性及相频特性均具有很好的近似。最终设计的分数阶PID框图如图4所示,在比例积分微分环节之后加入了分数阶积分和分数阶微分环节。
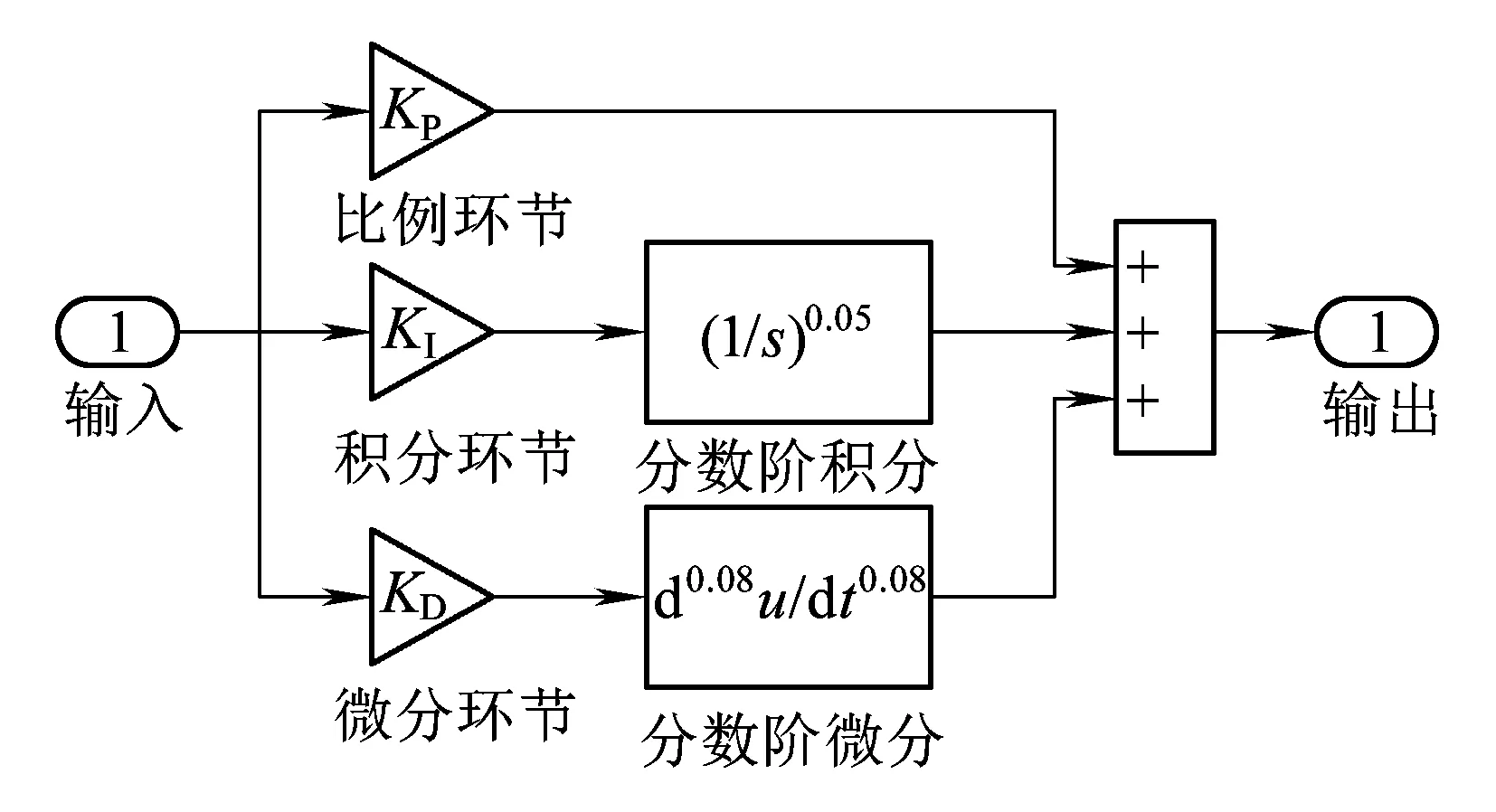
图4 分数阶PID仿真框图
Oustaloup滤波器为
(10)
其中
3 实验及结果
3.1 模型建立
建模计算所依据的数据是通过现场采集的南京地铁一号线A型车行车数据。行车记录仪对南京地铁一号线采集到的部分实际数据如图5所示。
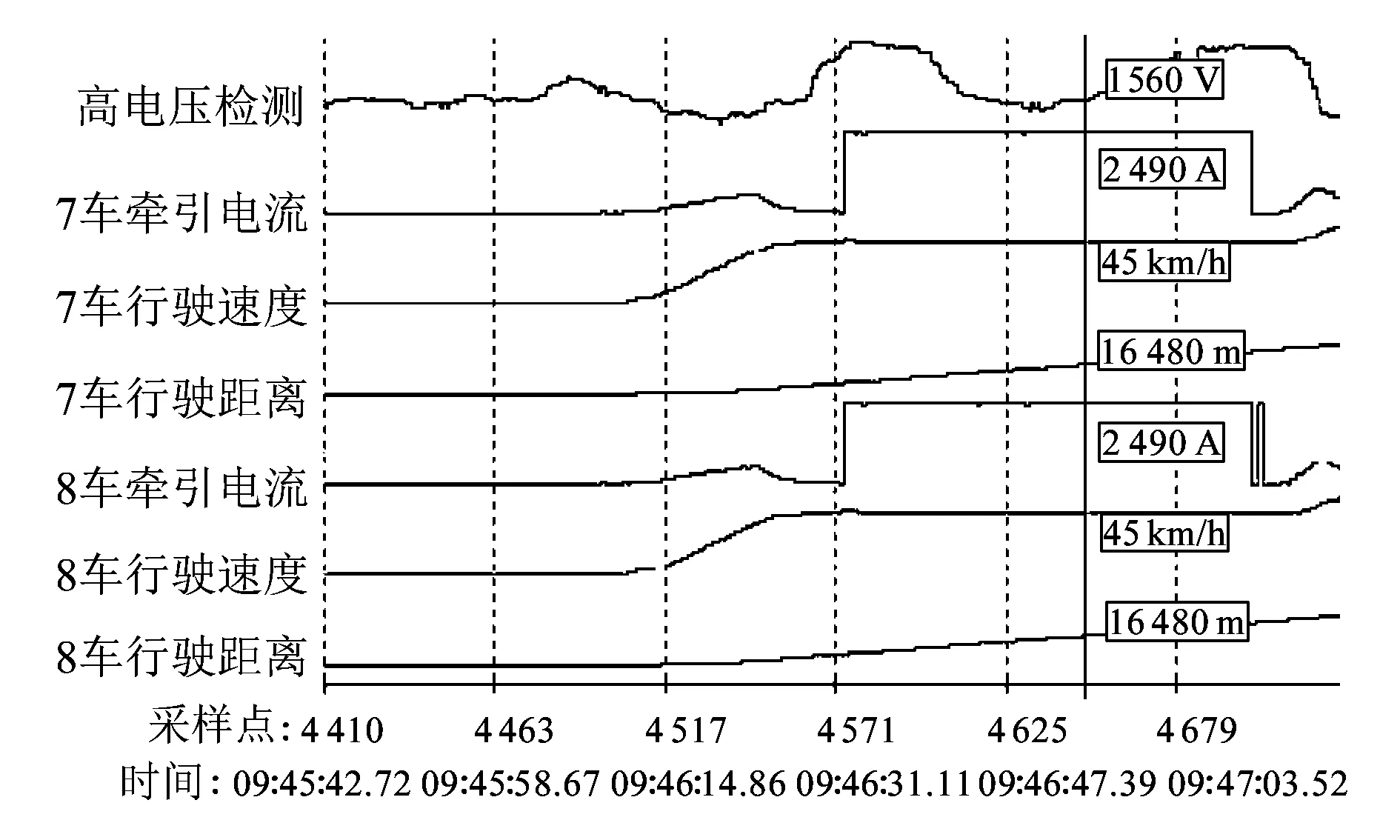
图5 行车记录仪获得的部分实际数据
A型车的列车编组为:=Tc*Mp*M=M*Mp*Tc=。其中:*为半永久式牵引杆;=为全自动车钩;Tc为有司机室的拖车;Mp为有司机室带受电弓的动车;M为无司机室的动车。列车长度为140 m,总牵引力为368 kN,最高运行速度为80 km/h。根据前述的列车运动模型,对南京地铁一号线的列车运动模型用MATLAB软件进行仿真,加入列车牵引制动特性曲线。仿真研究的重点是列车AW2荷载状态的技术指标。将记录仪采集到的AW2工况下一段数据运用最小二乘法计算,得到的基本阻力结果为
ω0=2.955+0.014v+0.002 2v2
同样,使用遗传算法对基本阻力系数进行计算,适应度为速度值和距离值两者的ITAE性能指标的乘积,并对基本阻力参数取值范围加以限定,以减少迭代次数,适应度变化曲线和种群均值变化曲线如图6、图7所示。

图6 适应度变化曲线
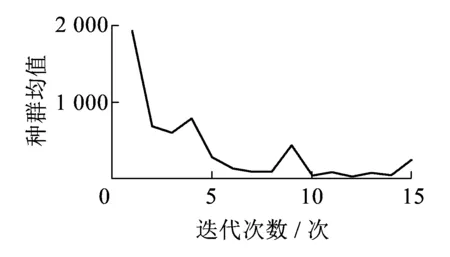
图7 种群均值变化曲线
由图7可以看出使用遗传算法在迭代5次之后可得到满足精度的适应度,依此将列车运行仿真模型中的基本阻力模块设置为
ω0=5.1+0.039 1v+0.001 1v2
依据以上计算得出的参数,对两种算法进行对比,见表2。
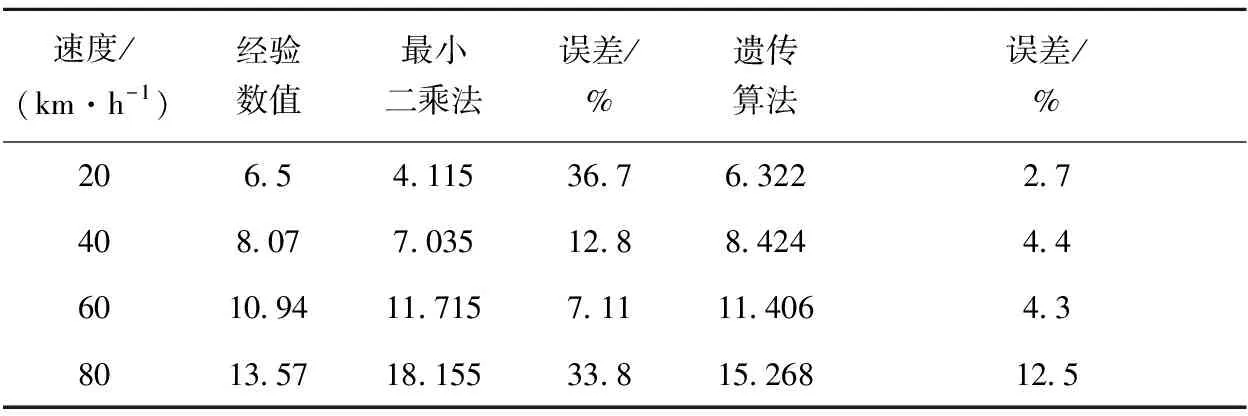
表2 最小二乘法和遗传算法的对比
由表2可以看出,遗传算法得到的结果与经验值更为贴近,可以作为实际列车的阻力修正参数。使用其他AW2工况区间数据进行验证,测得的ITAE性能指标均在误差范围内。对AW0工况区间数据进行处理,基本阻力结果为
ω0=1.095+0.364v+0.001 3v2
用遗传算法得到的参数来完善模型,输入实际的牵引制动档位和附加阻力值,将仿真得到的速度结果与实际运行所采集到的速度值进行比对,结果如图8、图9所示。
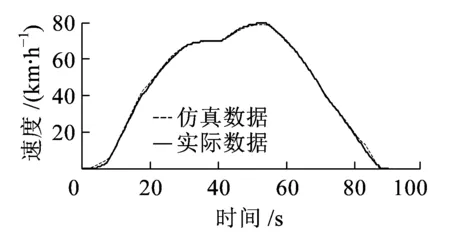
图8 列车运动模型下AW2工况的仿真速度曲线
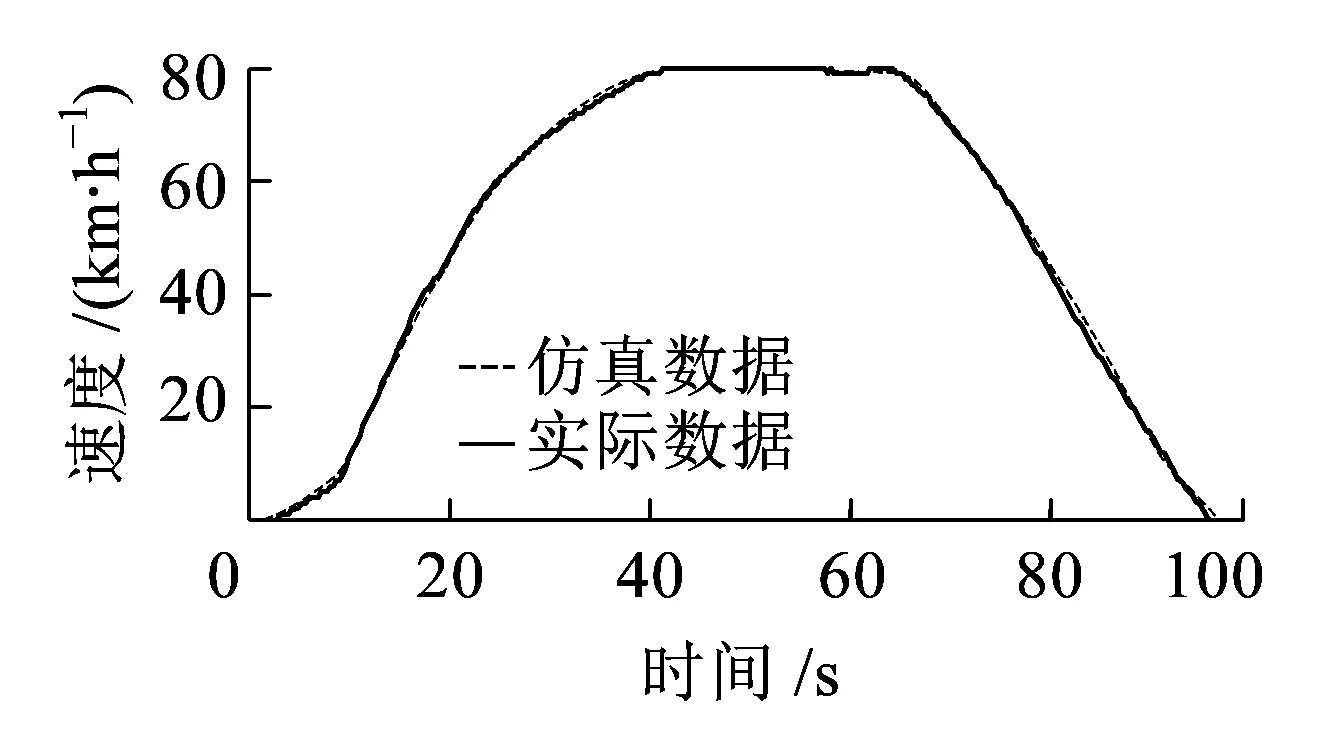
图9 列车运动模型下AW0工况的仿真速度曲线
由图8、图9可以看出,优化后的列车运动模型在各种工况下都能够很好地与实际采集到的数据相吻合,仅在低速时有一定的误差。依据此算法模型,可以从实际线路速度状态信息中得出更为准确的列车基本阻力实际系数值。
3.2 分数阶PID控制算法结果
基于上述优化的列车运动模型,研究列车的自动控制算法。现阶段大部分列车自动驾驶系统的控制算法采用的是传统PID控制或自适应PID控制。为此,本文分别使用传统PID控制方法和分数阶PID控制方法对列车速度进行控制。由于最终控制目标为多目标,且部分目标不易量化处理,所以使用传统经验及递进方式更改控制参数,分别得到两种控制方式的最优解,在最优解下的阶跃响应如图10所示。
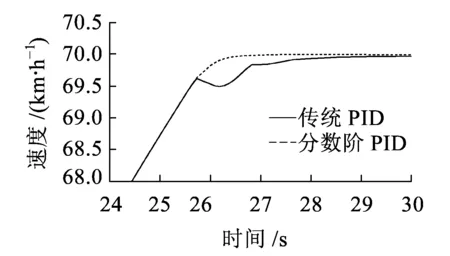
图10 传统PID和分数阶PID阶跃响应
从图10可以看出,在25.8 s之前两条曲线重合,此时两者都是以最大牵引力加速。由于存在区间限速,两者都不可以存在超调量。分数阶PID能够更快地达到控制目标,与此同时,传统PID的稳态误差为0.03 km/h,分数阶PID的稳态误差为0.015 km/h,分数阶PID稳态误差更小,整体在阶跃响应中优于传统PID。传统PID控制参数和分数阶PID控制参数见表3。

表3 控制器参数
以列车的运行速度作为新建运动模型输入量,使用传统PID控制算法和分数阶PID控制算法分别进行响应追踪。考虑到ITAE能够较好地抑制长时间存在的误差,瞬态响应的振荡性小,且对参数具有良好的选择性和敏感性,将速度的ITAE性能指标作为控制指标。得到结果如图11所示,可以看出采用分数阶PID控制算法对设定速度的控制品质优于传统PID。

图11 两种算法的ITAE指标
为了进一步进行比较,采用线路的列车限速曲线作为控制目标,应用分数阶PID控制算法进行控制,与实际的列车运行曲线相对比,分数阶PID控制结果速度更快,用时更短,速度曲线如图12所示。
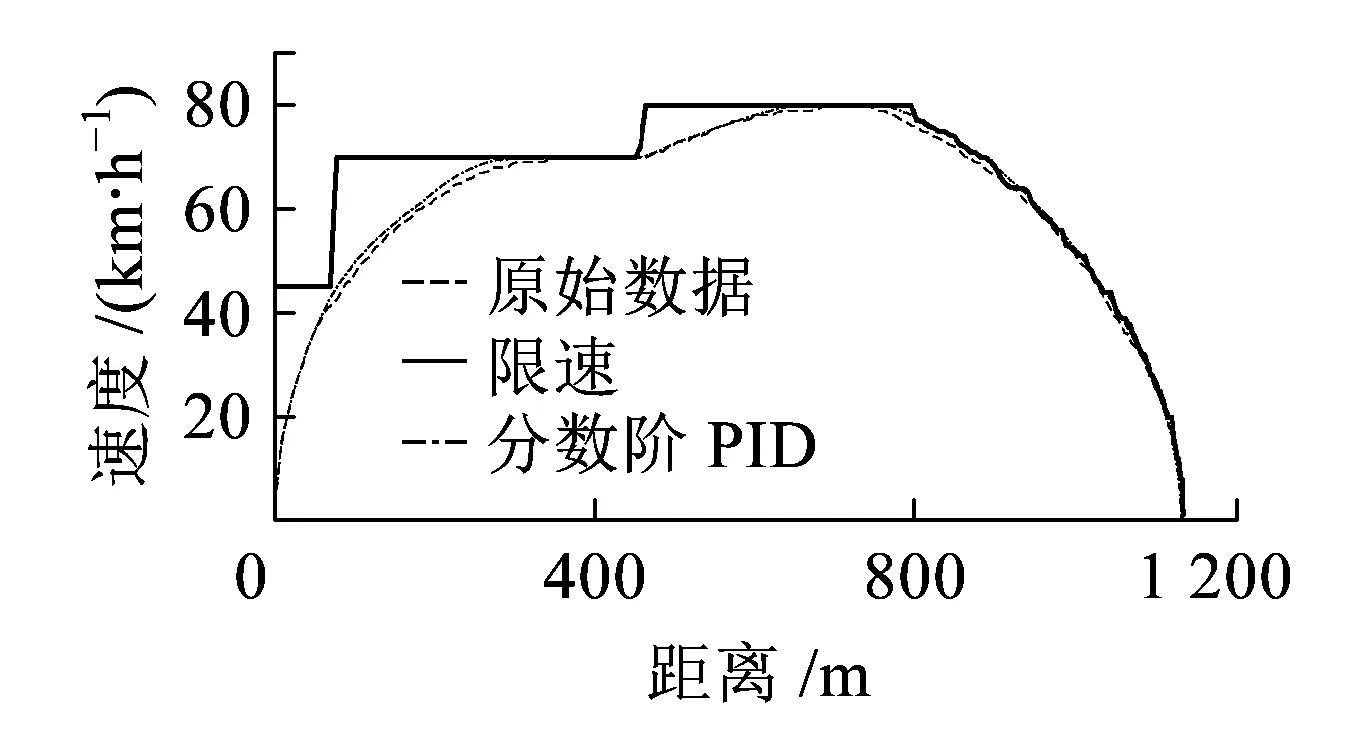
图12 速度曲线
分数阶PID控制算法通过调整参数,可以使其没有超调量,在ATP设定的限速下运行,快速达到目标值,档位切换平稳等多个目标同时得到满足,档位控制结果如图13所示。
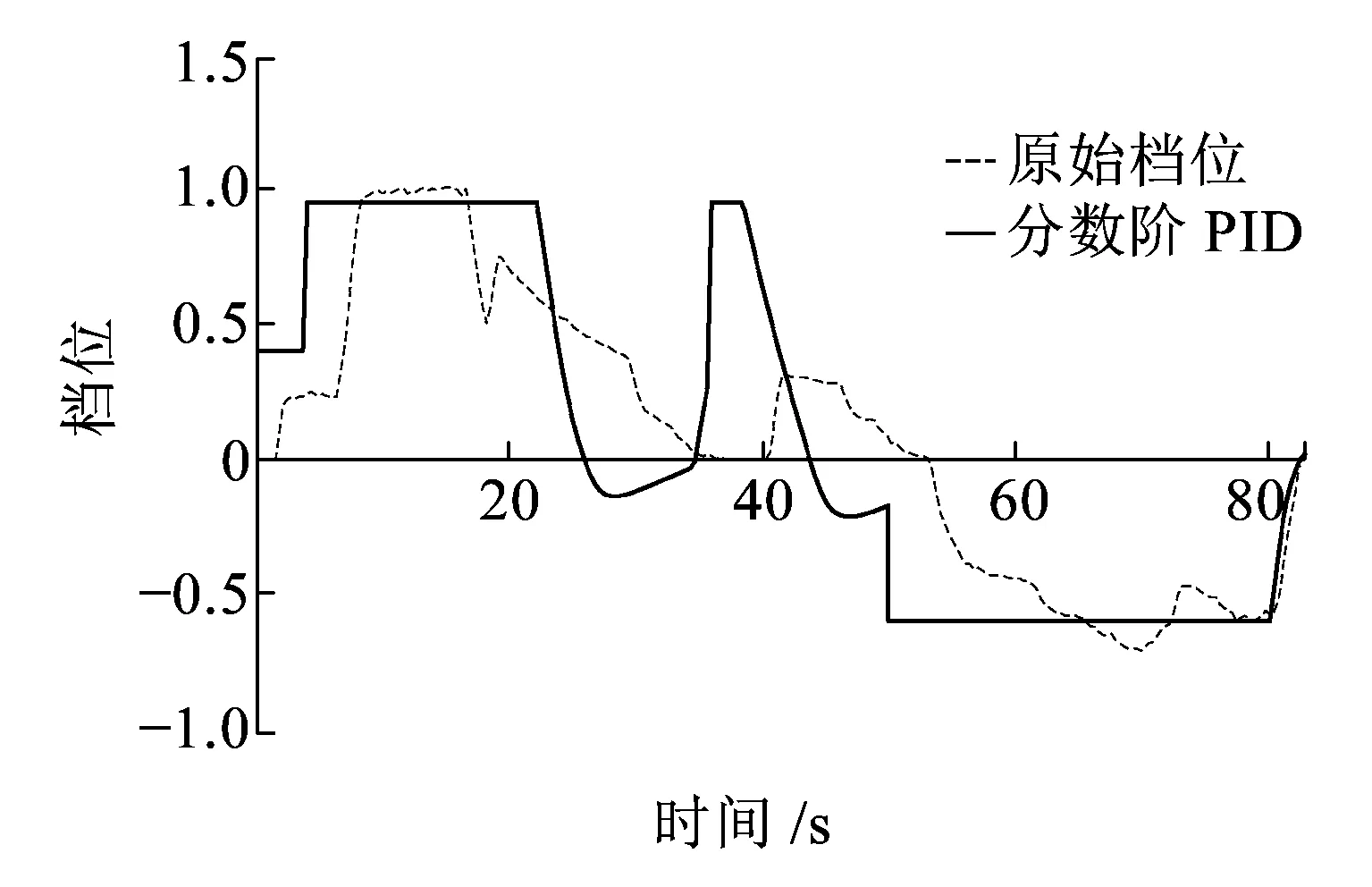
图13 分数阶PID档位控制结果
对分数阶PID控制算法参数进行整定,结果见表4。

表4 控制器参数
使用传统PID控制算法时,无法找到同时满足没有超调量、速度无振荡、时间尽量短、档位切换平滑多目标的参数,满足前3个目标的档位控制结果如图14所示。

图14 传统PID档位控制结果
从档位切换来看,传统PID在精度提高的同时稳定性就会下降。而分数阶PID在保证精度和速度没有超调量的同时,降低了切换频率,加速度变化较为平稳,从而减少了顿挫,提高了乘坐舒适度。分数阶PID能够克服变化带来的不确定影响,从而提高系统的可靠性。
4 结束语
本文对传统的列车运动模型进行改进,加入列车牵引制动特性,应用遗传算法对不同线路条件、车辆工况下的基本阻力系数进行识别计算。新建立的模型误差小,较现有的理想模型更贴近于实际的列车。在此基础上,将分数阶PID控制方法应用到上述列车运动模型中的ATO系统。仿真实验结果表明,使用分数阶PID控制方法进行列车速度控制时,能够使速度跟随更快,控制精度更高,同时减少了顿挫,提高了舒适度,总体性能优于传统PID控制。
本文方法对列车的档位控制仍有较大的提升空间,对列车基本阻力系数的辨识也可以使用不同的方法,如卡尔曼滤波。同时,分数阶PID控制算法中参数的选定也是未来研究的方向。

