基于粒子群算法的服装生产流水线编制

闫亦农， 刘立枝， 雒彬钰， 崔慧荣

(内蒙古工业大学 轻工与纺织学院， 内蒙古 呼和浩特 010080)

随着科技的发展及消费者对服装要求的提高，计算机辅助服装流水线生产越来越受到人们的关注，基于粒子群算法的智能化优化编排在诸多行业都有研究。

粒子群算法可有效地解决离散型组合优化问题[1]。基于粒子群优化算法的流水线优化在工程、机械方面的函数优化、计算机防护和决策支持等领域已有较多的研究，大都以粒子迭代为作用机制[2-4]，实现有效缩短粒子路径的目的。随着对优化算法研究的深入以及对智能优化的要求，遗传优化算法、蚁群优化算法、结构方程模型等逐渐运用于服装生产流水线的优化中，用来提高生产流水线的平衡[5-7]。

但是关于粒子群算法应用服装生产流水线优化方面的研究很少，研究尚不成熟。本文在前人研究基础上，结合服装吊挂系统，参考其他行业粒子群算法优化生产思想，以计算机编程软件为依托，对服装生产流水线优化进行了研究。

1 生产流水线平衡指标分析

缝制流水线平衡评价指标是评价服装企业生产流水线生产工序是否达到优化，人员是否得到最佳配置的重要指标。平均流水节拍、工作地数、编制效率和均衡指数是生产流水线平衡的4项重要评价指标[8]。通过评价指标可发现流水线上存在的问题，并针对问题对缝制流水线进行重组优化[9]。通过对生产流水线的具体分析，列出了评价指标的公式见表1。

表1 流水线平衡度评价指标Tab.1 Evaluation index of line balance

注：SPT为理论平均节拍；N为作业工人数；k为流水线的工序数；ti为第i道工序作业时间；T为一天作业的总时间；Q为日产量；Wmin为最小工作地数；T′为1件服装的总加工时间；η为编制效率；maxT(Si)为瓶颈节拍；SSI为均衡指数；T(Si)为第i个工作地的节拍。

2 基于粒子群的服装生产线编制原理

服装生产流水线编制问题属于离散组合优化问题，这与普通的组合优化问题不同，它不能用公式进行系统化的求解，具有多项式复杂程度的非确特性(NP)。通过借鉴遗传算法中染色体交叉和变异等思想[10]，结合粒子群算法快速搜索最优值的能力，对服装生产流水线进行编排。因为遗传算法中的交叉、变异思想能更好地实现工序重新组合和再分配，但在搜索最优位置的能力方面，粒子群基于速度优势，能更准确、快速地搜索到最优位置，减少迭代次数，避免发散。

2.1 粒子群优化算法流程的改进设计

基于遗传算法，对粒子群优化算法进行重新改进设计，其改进后的设计流程[11-12]如下。

步骤1：种群初始化，设定种群规模S，交叉概率J，变异概率B，迭代次数X，随机产生粒子群的初始位置，即随机赋予各工序初始位置；

步骤2：依据当前初始位置，计算适应度值(平均节拍界限)，并将该值作为个体极值，然后确定全局极值及位置；

步骤3：通过运用遗传算法中的思想，对粒子群进行交叉和变异；

步骤4：利用遗传算法进行交叉和变异后，计算各个体的适应度(各节拍界限)，将各粒子的适应度与先前适应度进行比较，判断是否优于先前的个体极值位置，若满足，新的个体极值位置代替原个体极值位置；若不满足，原有个体极值位置不变；

步骤5：通过个体极值(工作地节拍)，重新更新了粒子的位置，然后找出全局最优位置；

步骤6：判断程序运行是否满足终止条件，如果满足，则执行步骤7，如果不满足，则步骤3将被继续运行，直至满足终止条件；

步骤7：输出全局极值(工作地节拍)及全局极值位置(最佳工序排序)。

改进后的粒子群优化算法的流程，如图1所示。

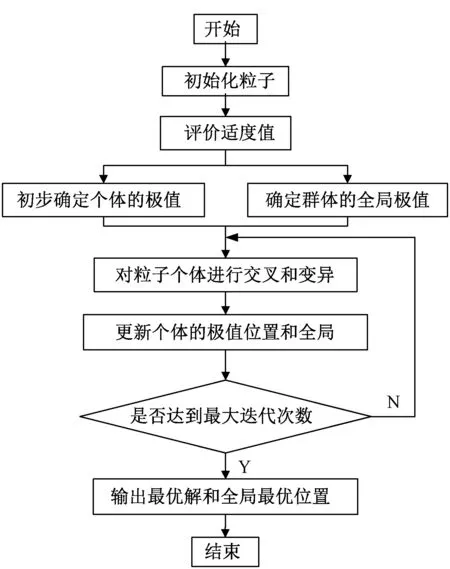
图1 改进的粒子群算法流程图Fig.1 Improved particle swarm algorithm flow chart

2.2 服装缝制流水线数学模型的构建

数学模型是高效处理服装生产线编制问题的重要组成部分，是决定流水线编制能否正常进行的基础。而在评价流水线平衡的指标中，均衡指数SI是评价服装流水线作业平衡的重要指标。本文将其最小化，并作为目标函数。流水线作业是一个宏观的过程，要想实现流水线的最佳优化，必须要对流水线作业的相关设备、数据、专业术语等进行细致、详细的了解，然后通过数学的思想，将流水线作业的相关参数建立数学的模型。基于此，建立了符合流水线编制的数学模型如下：

式中：确定作业工序集A={1，2，…，M}的一个划分{Si|i=1，2，…，W}，其中，M为工序总数。Min(SSI)为最优均衡指数值。

在运用均衡指数建立数学模型时，有如下约束条件：

1)单件服装作业的总时间与实际作业的总时间在数值上相等；

2)工序分配时，各工序节拍应控制在[SPT(1-5%)，SPT(1+5%)]范围内；

3)作业员对所负责工序熟练程度基本一致；

4)在作业过程中，同一个工作地或不同的工作地之间，作业工序要遵循生产的前后关系，保证流水线作业流畅；

5)在工序组合过程中不同工作性质的工序尽量不要组合在一起，当且仅当同种作业性质的工序组合排列后编制效率低于85%不符合企业生产时，方可将部分2种不同作业性质的工序进行组合。当将2种不同作业性质的工序组合后编制效率仍低于85%，可在个别工作地将3种不同作业性质的工序进行组合，同时增加该工作地总作业时间的5%，以此降低流水线因不同性质工序组合带来的误差。

2.3 操作系统软件的建立

采用Windows 7作为服务器操作系统，My Eclipse 9.0 作为开发工具，Tomcat 5.0 作为系统Web应用服务器，Java语言开发工具包(JDK)作为系统的运行平台，Java作为编程的基础语言，数据库采用My SQL数据库。

服装缝制流水线编制系统为体现系统化、一体化原则，建立用户登录的权限。登录系统后，用户进入主界面，对服装吊挂生产流水线优化系统中的相关数据进行有效管理。主界面的左侧是系统主要的4大信息模块，每个模块都有下拉菜单，也是模块展现功能的指令。本文系统中的用户一般为企业车间的管理人员以及车间的技术员。

服装生产流水线优化系统的功能模块设计，其出发点是实用、简单、操作性强。在工序信息管理功能中，主要包括3方面的内容：工艺流程、工序信息和流水线优化。单击生产工序信息管理，会出现下拉菜单，通过流水线优化可直接实现服装缝制流水线智能化编制。

此外，在对服装缝制流水线进行计算机编制时，需要对车间的设备状况和人员配备状况进行了解和分析，设备及人员数量是否符合计算机优化的结果，资源是否得到合理、充分的利用等。

3 生产实例分析

为进一步体现服装缝制流水线编制系统的实际可操作性和普遍性，对男士制服裤装的缝制流水线进行编制，并计算各平衡指标，使其达到精益化生产的要求。

3.1 男式制服裤装的生产流程

男式制服裤装的生产工序流程如图2所示。其详细描述了各工序之间的先后关系、各工序的作业时间及作业性质。

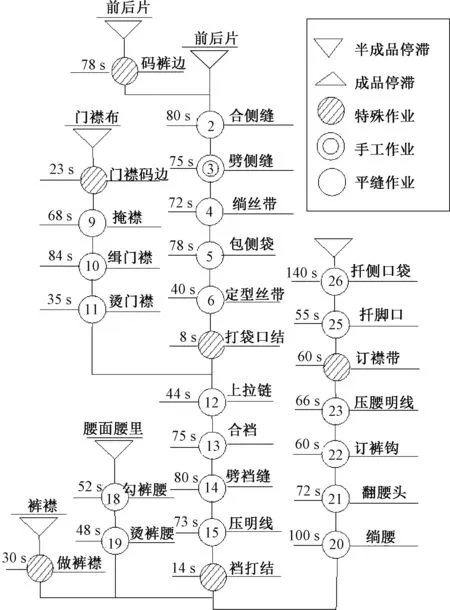
图2 男式制服裤装生产工序流程图Fig.2 Production process flow chart of uniform male trousers

3.2 服装缝制流水线编制

3.2.1生产流水线编制参数的设定

运用基于粒子群算法的流水线智能编制系统对服装生产流水线进行编制，首先计算出男士制服裤装流水线的理论最小工作地数，并确定流水线上的理论平均节拍。在确定最小工作地数和理论平均节拍的基础上，运用基于粒子群算法的服装生产线智能编制系统对男士制服裤装的流水线进行编制。已知该款裤装的目标日产量Q=220件/d，有效作业时间t为9 h/d，单件服装缝制总时间t′为1 580 s，通过表1中公式(1)计算，得出理论平均节拍为147 s。

在求出理论平均节拍的基础上，根据表1中公式(2)计算，得出最小工作地数Wmin为11。在编制系统内输入以上2项参数，为后续智能化生产流水线编制做好准备。

3.2.2优先区域的划分

根据表1，制定制服男裤裤装作业任务图。通过优先区域划分确定作业高度，同时确定每道工序的前驱工序和紧后工序。将优先区信息录入数据库，为编制系统编制男士制服衬衫流水线做准备，优先区域划分如图3所示。

图3 男式制服裤装优先区域划分图Fig.3 Priority area division graph of uniform male trousers

3.3 服装缝制流水线编制结果

在系统软件相应界面输入男式制服裤装的种群规模、最小工作地数、迭代次数等相关参数，输入参数后单击流水线优化，经过系统运算就会呈现其流水线的编制结果，每个工作地的工序组合及作业时间分配如表2所示。

3.4 生产作业分析

作业时间曲线能够直观形象地反映生产的同步化程度，智能编制男裤裤装的作业时间曲线如图4所示。可见：流水线平均节拍为147 s；各工作地工序节拍均在节拍界限范围内，缝制流水线平衡性较好，总体可实现生产的同步化。

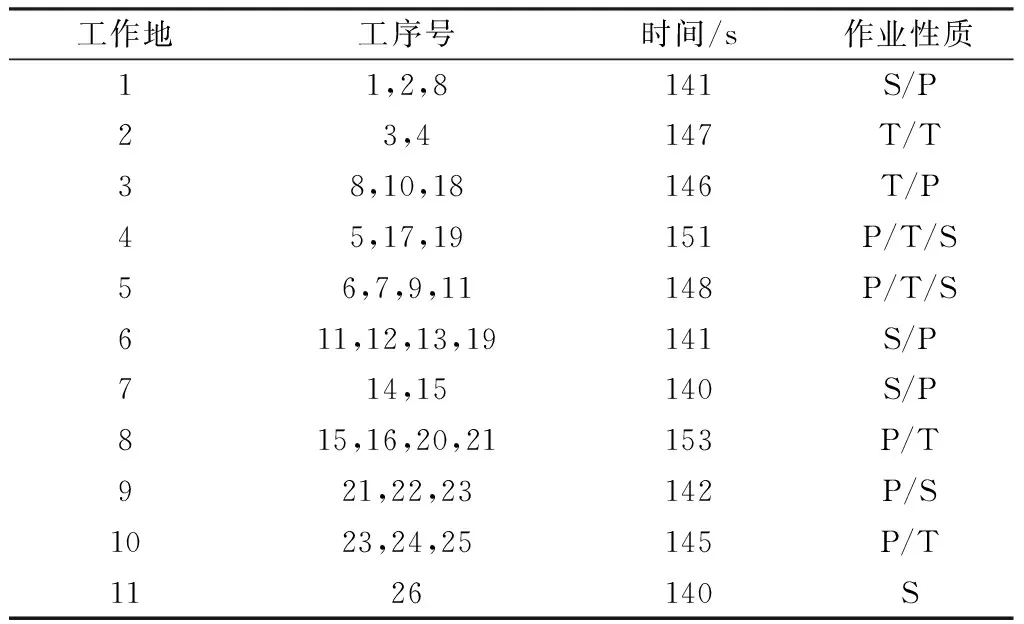
表2 智能编制制服男裤流水线工序分配表Tab.2 Intelligent design uniform male trousers pipeline process distributionTable

注：P表示平缝作业；S表示手工作业；T表示特殊作业。

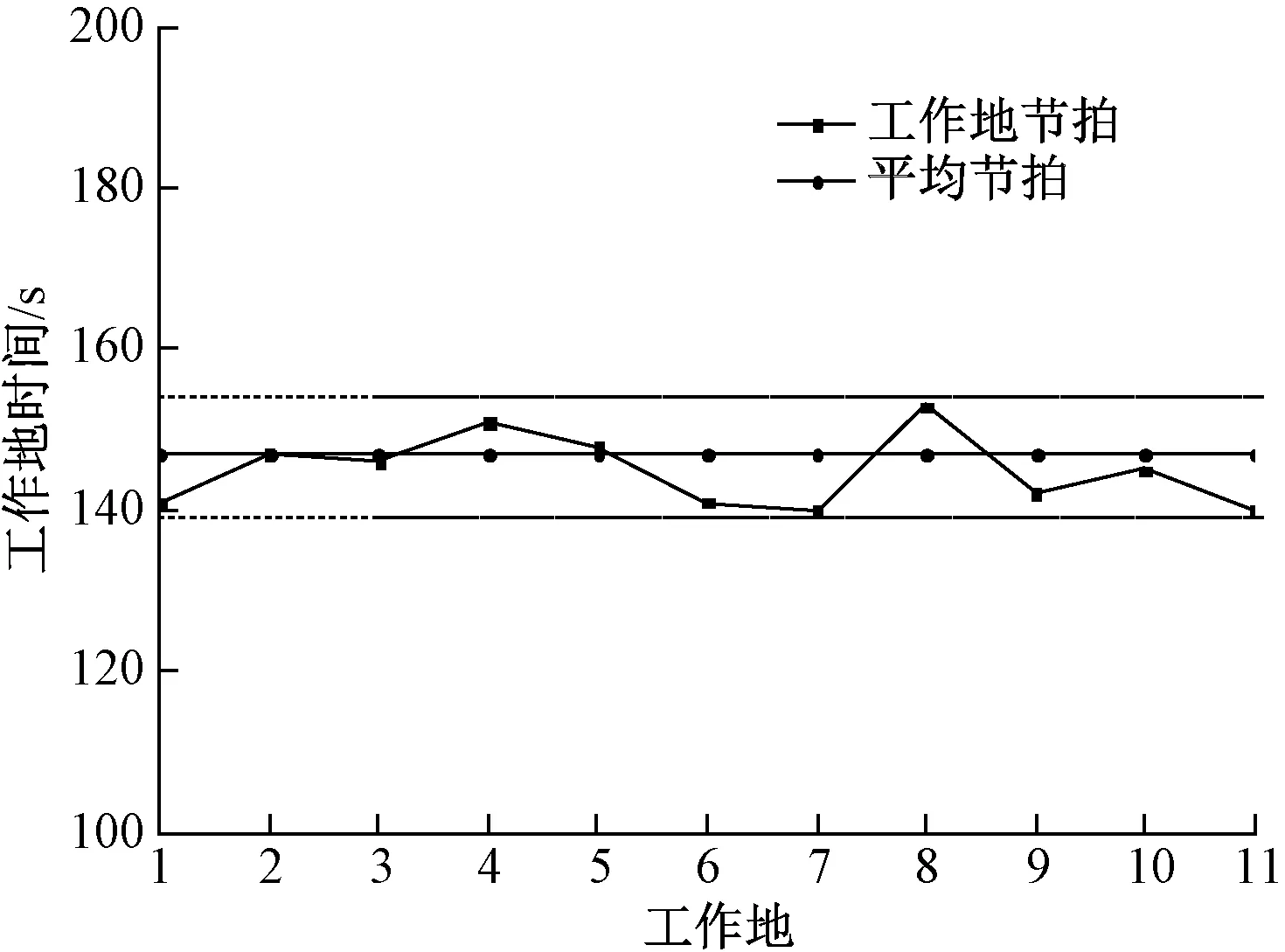
图4 生产线SPT与编制效率关系图Fig.4 Relationship between of SPT and establishment efficiency of assembly line

3.5 平衡指标结果分析

依托服装吊挂系统，运用粒子群优化算法对制服裤装缝制流水线进行编制，计算出表征服装缝制流水线平衡的平衡性指标。均衡指数为16.5，编制效率η为96.1%，最小工作地数Wmin为11，编制效率η远远高于85%，可运用于实际生产，且满足服装企业精益化生产要求。

4 结 论

通过实例验证，可实现基于粒子群算法服装生产流水线的智能化编制。通过智能化编制的制服男裤生产流水线各工位节拍相对平稳，均衡指数为16.5，编制效率为96.1%(≥85%)，最小工作地数为11，符合企业精益化生产需要。