液压伺服驱动机械手运动轨迹跟踪控制误差研究
魏鸿儒,刘益标,陈 均
(1.吉林铁道职业技术学院 铁道运输学院,吉林 吉林 132200; 2.广东工贸职业技术学院 机电工程学院,广州 510510;3.广州市特种机电设备检测研究院 研发部,广州 510180)
近些年,工业自动化得到了迅速发展,使机械手的应用也越来越广泛,例如,机械手已应用在煤矿开采、海洋探测及医疗救援等许多领域.机械手驱动大多采用液压系统,主要是因为液压机械手采用液压油作为驱动动力的介质,具有结构紧凑、运动稳定及定位精度高[1-2]等优点.在日常工作环境中,经常遇到塌方、爆炸、深水作业及化学物泄露等,就需要自动化机械手代替人工从事生产劳动.要完成自动化作业,就必须保证机械手运动轨迹能够按照期望轨迹进行运动.目前,人们对智能控制的要求越来越高,这就要求机械手运动轨迹定位精度也随之提高.因此,研究高精度的液压机械手控制,对于自动化产业的发展具有重要的意义.
为了提高机械手液压驱动运动轨迹定位精度,使机械手自动化控制能够更好地为人们服务,国内外学者对机械手液压驱动控制展开了研究.例如:文献[3-4]研究了工程机械臂液压驱动PID控制系统,建立了液压系统模型,推导液压缸体积流量方程式;文献[5-6]研究水下液压机械手PI控制系统,分析系统控制的组成和实现方法,提高了系统控制的稳定性;文献[7]研究液压机械手PLC控制系统,设计了液压机械手控制系统总体方案,给出控制系统硬件电路接线图,简化了控制系统.以往学者研究的液压机械手结构简单,运动轨迹跟踪速度较快,但是作业精度较差,无法满足高精度轨迹定位的要求.对此,本文建立平面机械手液压驱动简图模型,给出机械手末端执行器运动的几何方程式;分析了伺服阀控制原理,推导出伺服阀控制流量方程式;引用改进粒子群算法优化神经网络PID控制,并且将改进神经网络PID控制效果通过Matlab软件进行仿真验证,输出机械手液压驱动轨迹跟踪误差曲线,并与PID控制轨迹跟踪误差进行比较和分析,为深入研究机械手液压驱动控制提供理论基础.
1 机械手运动分析
本文采用机械手液压驱动机构为研究对象,其平面简图如图1所示.
机械手关末端执行器位置为
(1)
式中:xw,yw分别为末端执行器x轴和y轴坐标;l1,l2,l3为机械手连杆长度;θ1,θ2,θ3为连杆与水平面之间的夹角.
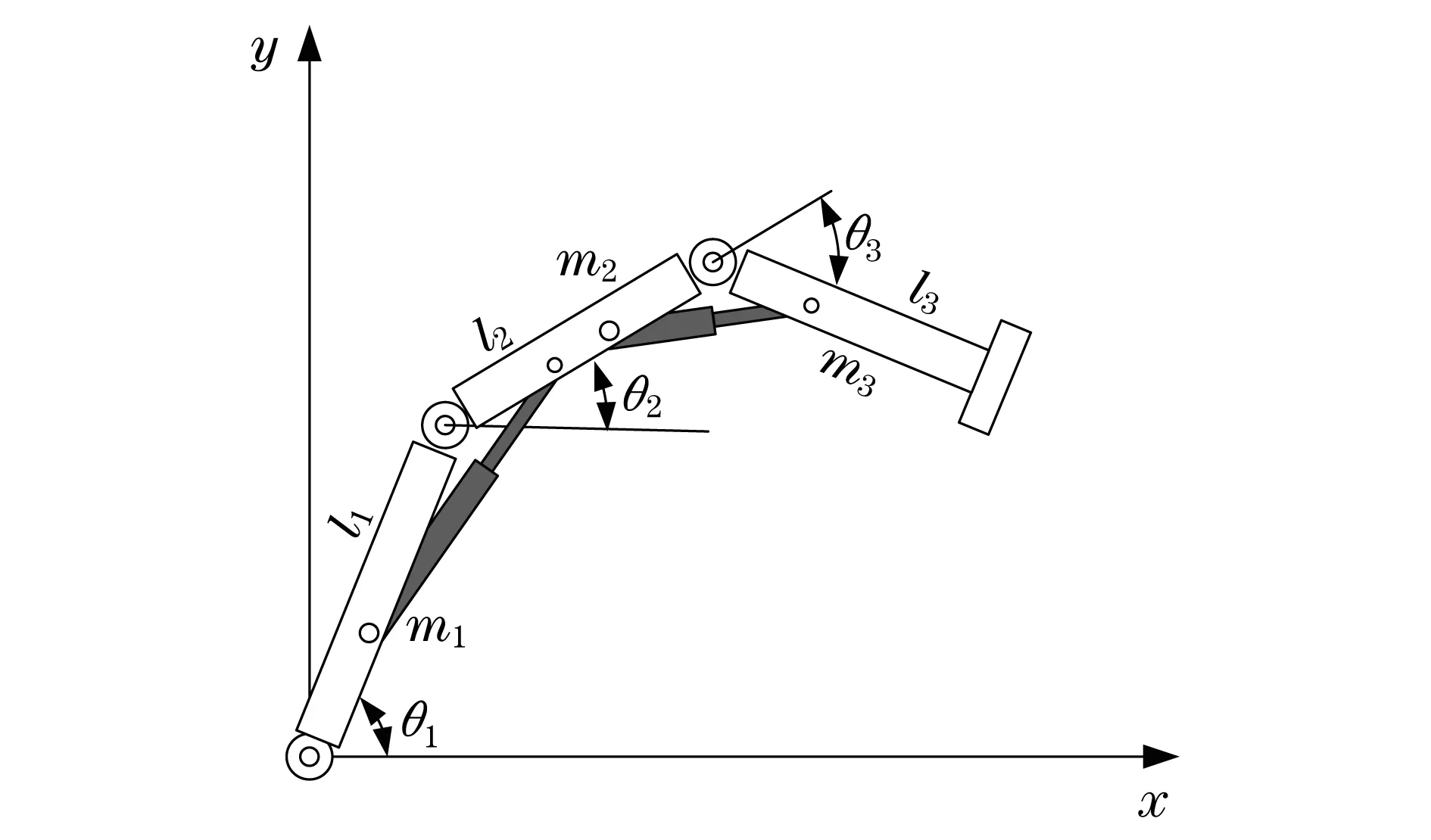
图1 机械手液压驱动简图Fig.1 Hydraulic drive diagram of manipulator
机械手末端执行器采用液压缸驱动,实现末端执行器的实际运动轨迹尽可能与期望运动轨迹吻合.执行器跟踪误差定义为
(2)
式中:xd为期望运动轨迹;x为实际运动轨迹.
2 伺服阀液压驱动
2.1 伺服阀
伺服阀是一种信号放大装置,将弱电信号转换为驱动液压缸的功率信号.在PID控制器中输入弱电流信号,转换后输出压力和流量信号.伺服阀工作原理为:输入的励磁电流,驱动励磁马达转动,通过喷嘴喷口和压力不同,使励磁马达转角变大,达到控制阀芯的运动.阀芯运动可以控制进油量,进而控制压力和流量的大小.
液压驱动传递函数[8]为
式中:ksy=Ki·(LCk)-1为位移增益,Ki为力矩马达力矩常数,Ck为挡板弹簧刚度系数,L为挡板长度;KQ为伺服阀流量增益;Cl为流量系数;Ps为进油压力;Pl为负载压力;A为阀芯端面积;J0为挡板转动惯量;M0为阀芯质量;x0,A0为阀芯中位值;Ckm为力矩电机弹性力矩系数;ξv为阀芯阻尼比.
2.2 液压驱动
伺服阀将液压缸的流量和压力信号转换为驱动机械手的推力和位移信号.
伺服阀阀口流量方程式[9]为
式中:Q1为伺服阀入口流量;Q2为伺服阀控制流量;P1为负载进口压力;P2为负载出口压力;X为伺服阀阀芯位移;Q为流体密度;T为窗口面积梯度;Cd为流量系数.
负载流量方程式[9]为
式中:n=A2/A1为流量比;PL=P1-P2为负载压力.
液压缸伺服阀控制的流量连续方程式[9]为
(12)
Ve=2V[n3+V1(1-n3)/V]·(1+n2)-1
(13)
式中:Cp为泄露系数;Be为振动系数;Ve为液压缸等效容积;Ame=(A1+A2)/2为等效活塞面积;V=LA1为液压缸最大容积.
3 改进神经网络控制
3.1 改进粒子群算法
粒子群算法(Particle Swarm Optimization,PSO)是近些年发展的寻优算法.在PSO搜索过程中,粒子自身速度v和位置X通过个体极值pt和群体极值gt不断更新,其更新公式[10]为
vt+1=ωvt+c1r1(pt-Xt)+c2r2(gt-Xt)
(14)
Xt+1=Xt+vt+1
(15)
式中:vt,vt+1分别为迭代前速度和迭代后速度;Xt,Xt+1分别为迭代前位置和迭代后位置;ω为惯性权重;pt,gt分别为个体极值和群体极值;c1,c2为速度更新系数,区间为[0,2];r1,r2为随机数,区间为[0,1].
为了充分发挥局部和全局搜索能力,惯性权重ω进行改进后为
(16)
式中:ω0为初始惯性权重;ω1为最大迭代次数的惯性权重;t为当前迭代次数;T为最大迭代次数.
3.2 改进神经网络PID控制器
神经网络包含输入层、隐含层和输出层.
在神经网络输入层中,有2n个神经元,输出与输入数据相等,即
(17)
在神经网络隐含层中,有3n个神经元,分别为比例神经元n个、积分神经元n个和微分神经元n个.各个神经元的输入值都是相同的,计算公式为
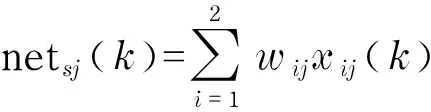
(18)
隐含层输出值计算公式互不相同,比例神经元、积分神经元和微分神经元输出计算公式分别为
式中:s为子网络序号;j为子网络隐含层神经元序号;xsi(k)为子网络输入层神经元输出值;wij为子网络输入层与隐含层之间连接权值.
在神经网络输出层中,有n个神经元,组成n维输出量,其计算公式[11-12]为
(22)
式中:h为输出层神经元序号;usj(k)为隐含层神经元输出值;wjk为隐含层与输出层之间连接权值.
在控制过程中,采用梯度修正法修正连接权值,使控制误差最小,其计算公式为
(23)
式中:n为输出节点数量;yh(k)为实际输出值;r(k)为理论输入值.
PID控制能够实现在线调节功能,其控制方程式[13]为
(24)
式中:Kp为比例系数;Ti为积分系数;Td为微分系数.
神经网络PID控制权值修正包括两个部分:输出层到隐含层,隐含层到输出层,其计算公式分别为
式中:η为学习速率.
采用改进PSO优化神经网络PID控制流程如图2所示.
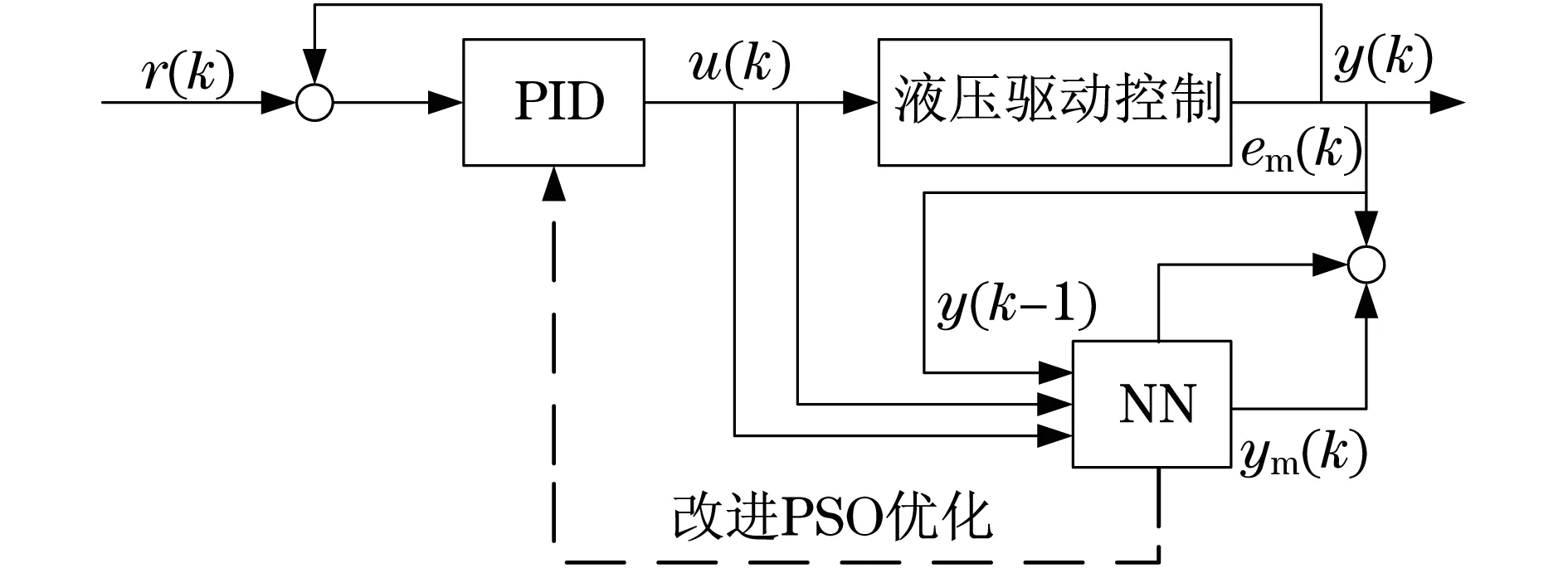
图2 改进神经网络PID控制Fig.2 Improved neural network PID control
4 优化与仿真
采用改进神经网络PID控制液压伺服驱动机械手运动轨迹,其初始条件设置如下:种群大小为150,迭代次数为300,初始惯性权重系数为ω0=0.85,最大迭代次数惯性权重系数ω1=0.55,速度更新系数c1=c2=2,随机数r1=r2=0.6,连杆质量分别为m1=3.5 kg,m2=2.5 kg,m3=1.8 kg,连杆长度分别为l1=0.6 m,l2=0.4 m,l3=0.3 m,比例系数Kp=4.75×105,积分系数Ti=1.87×105,微分系数Td=6.92×105.假设末端执行器运动轨迹为x=5sinπt,y=5cosπt,采用Matlab软件对改进神经网络PID控制进行仿真,其轨迹跟踪产生的误差如图3所示,而采用PID控制跟踪误差如图4所示.
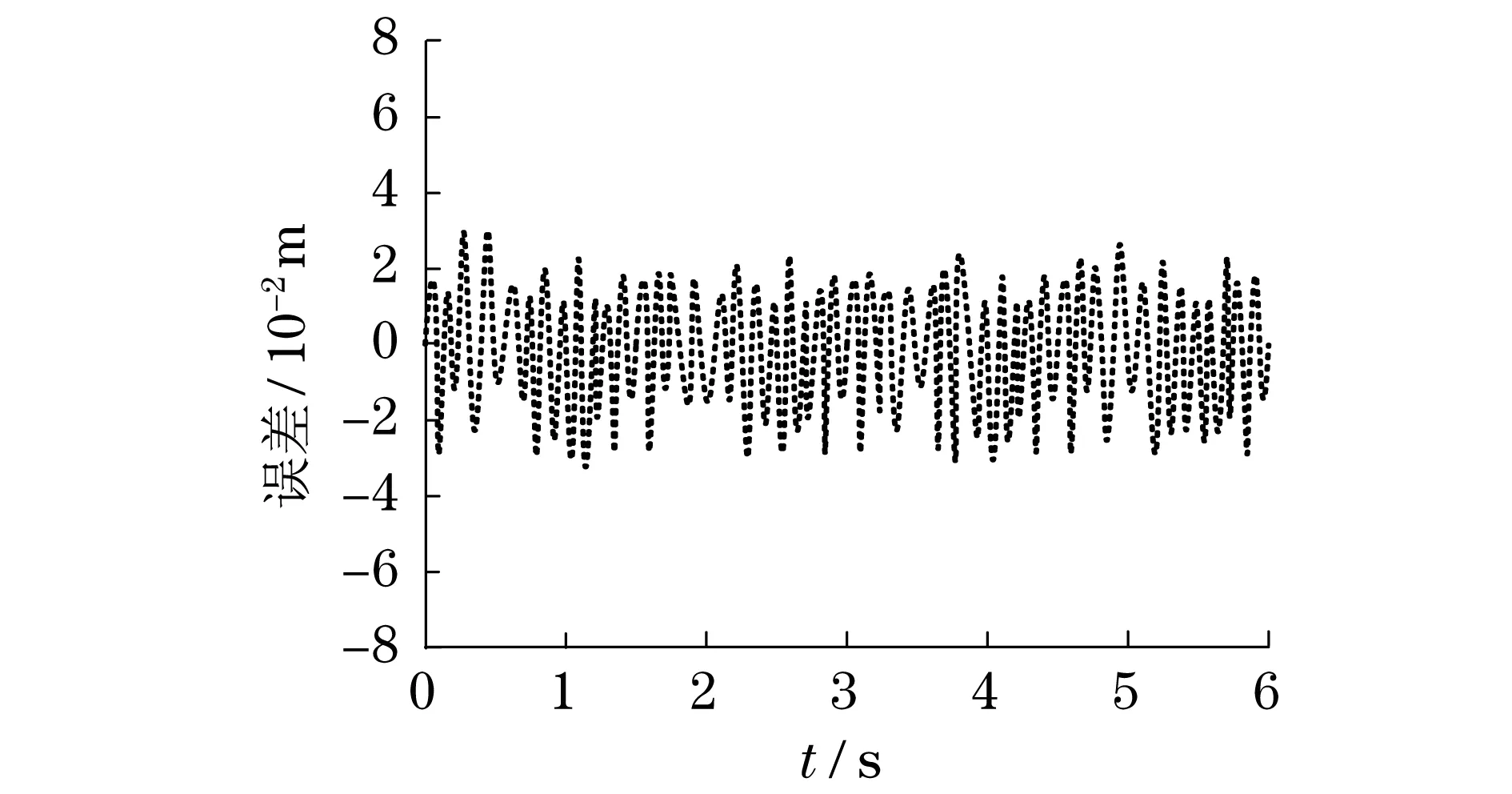
图3 液压机械手运动轨迹改进神经网络PID控制Fig.3 Improved neural network PID control
由图3运动轨迹可知:机械臂末端执行器跟踪轨迹与期望运动轨迹偏离程度较小,产生的最大误差为3.3×10-2m.由图5运动轨迹可知:机械臂末端执行器跟踪轨迹与期望运动轨迹偏离程度较大,产生的最大误差为6.7×10-2m.因此,采用改进神经网络PID控制机械臂末端执行器,能够更好实现机械臂末端执行器运动轨迹跟踪.
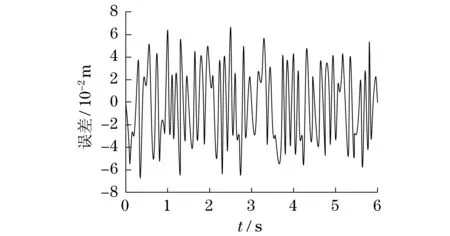
图4 液压机械手运动轨迹PID控制Fig.4 Trajectory control of hydraulic manipulator
5 结论
本文采用改进神经网络PID控制器驱动液压机械手末端执行器运动轨迹,主要结论如下:① 建立液压驱动机械臂简图模型,给出了末端执行器运动轨迹方程式;② 分析了伺服阀控制工作原理,给出了液压缸驱动流量控制方程式;③ 采用改进神经网络PID控制液压驱动机械臂运动轨迹,产生的误差相对PID控制较小.

