高超声速化学非平衡流动Navier-Stokes/DSMC耦合算法

李中华，党雷宁，李志辉,2

1. 中国空气动力研究与发展中心 超高速空气动力研究所，绵阳 621000 2. 国家计算流体力学实验室，北京 100083

高超声速飞行器在大气中飞行，经过激波压缩的高温气体，激波后的温度可达上万度，此时飞行器前方的绕流流场，特别是弓形激波附近流场，气体分子状态远离平衡态，不仅气体分子的移动温度、转动温度和振动温度存在着显著差别，而且会伴随着剧烈的化学反应[1-4]。特别是在稀薄过渡流区，化学反应具有强烈的非平衡特征，会对飞行器的力、热特性产生显著影响。随着载人航天和临近空间飞行器的发展，各类航天器在稀薄过渡流区飞行的时间越来越长，化学非平衡的影响尤为越突出[5-8]。

对于化学非平衡的处理，在数值模拟方法上，传统的计算流体力学(Computational Fluid Dynamics，CFD)技术一般通过求解连续流(克努森数Kn≤0.01)的三维Navier-Stokes流体动力学方程,耦合化学反应动力学模型对化学反应过程求解，发展出了多种高效的数值计算方法[9-12]。随着气体稀薄程度的增大，连续介质假设失效，基于Navier-Stokes方程的数值模拟方法会出现较大误差。在稀薄流区(Kn≥1)，基于粒子随机统计模拟的直接仿真蒙特卡罗(Direct Simulation Monte Carlo，DSMC)方法是处理各类非平衡流动的常用方法，得到了广泛的发展和应用[13-17]。随着Kn的减小，DSMC计算效率会越来越低，直至计算难以进行[18-20]。

处于中等Kn的过渡流区流动，无论在试验技术还是数值计算方面均是难于处理的一种流动[21-22]。为了研究过渡流区的数值模拟方法，众多研究者进行了各种尝试。基于Boltzmann模型方程的统一算法，取得了较好的效果，但目前还没有办法处理化学非平衡的流动[23-27]。基于CFD技术和DSMC方法的Navier-Stokes/DSMC耦合计算方法，在理想气体的耦合计算中，取得了很好的结果[28-30]，能够处理包含移动、转动、振动等非平衡过程，计算结果与全DSMC方法的结果很接近。在过渡流区，采用Navier-Stokes/DSMC耦合算法，能够代替全DSMC方法模拟高超声速非平衡流动[31-35]。

在理想气体的耦合算法基础上[36-40]，本文尝试开展高超声速化学非平衡流动的Navier-Stokes/DSMC耦合算法研究。基于包含化学非平衡流动的CFD和DSMC方法和软件，建立了过渡流区化学非平衡流动的Navier-Stokes/DSMC耦合算法。利用耦合计算方法，对高超声速二维圆柱绕流进行了模拟，与相关文献结果进行比较，验证化学非平衡Navier-Stokes/DSMC耦合计算的有效性。

1 数值模拟方法

1.1 CFD技术

对高超声速飞行器绕流问题，在连续流区域一般采用CFD算法求解Navier-Stokes方程组，可以得到准确的飞行器气动力特性，而且计算效率较高。

对于ns种组元的混合气体，三维化学非平衡流动控制方程包含ns个组元质量守恒方程，3个方向的动量守恒方程和1个能量守恒方程，具体形式为

(1)

式中：Q为守恒变量矢量；E、F、G为无黏通量矢量；Ev、Fv、Gv为黏性通量矢量；S为化学反应源项；t为时间坐标；x、y、z为3个方向坐标。

具有ns个组元的化学反应方程可以表示为

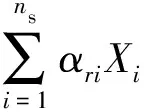
(2)

式中：αri、βri分别表示反应物和生成物的当量系数，下标“r”和“i”分别代表第r个反应以及第i个组元；Xi为第i个组元的分子式。

根据质量反应定律，式(2)中组元Xi的净生成速率为

(3)

式中：[Xi]=ρi/Mi为组元Xi的摩尔浓度，ρi为组元密度，Mi为组元分子相对质量；Rfr、Rbr为正向反应速率和逆向反应速率；kfr、kbr为正向反应速率系数和逆向反应速率系数。

本文使用Dunn&Kang的化学动力学模型。在Dunn&Kang的化学动力学模型中，正向、逆向反应速率系数根据修正的Arrhenius经验公式得到，即

(4)

式中：T为流场温度；A为置前因子；B为温度指数；C为反应活化能与普适气体常数的比值；下标“f”和“b”分别表示正向、逆向反应。

表1给出了5组元空气反应Dunn&Kang模型的正向和逆向反应速率系数计算中的各常数值[5]。

采用有限体积法离散控制方程，采用无波动、无自由参数的耗散格式(Non-oscillatory, containing No free parameters and Dissipative scheme,NND)离散无黏项、中心差分格式离散黏性项。NND格式为

(5)

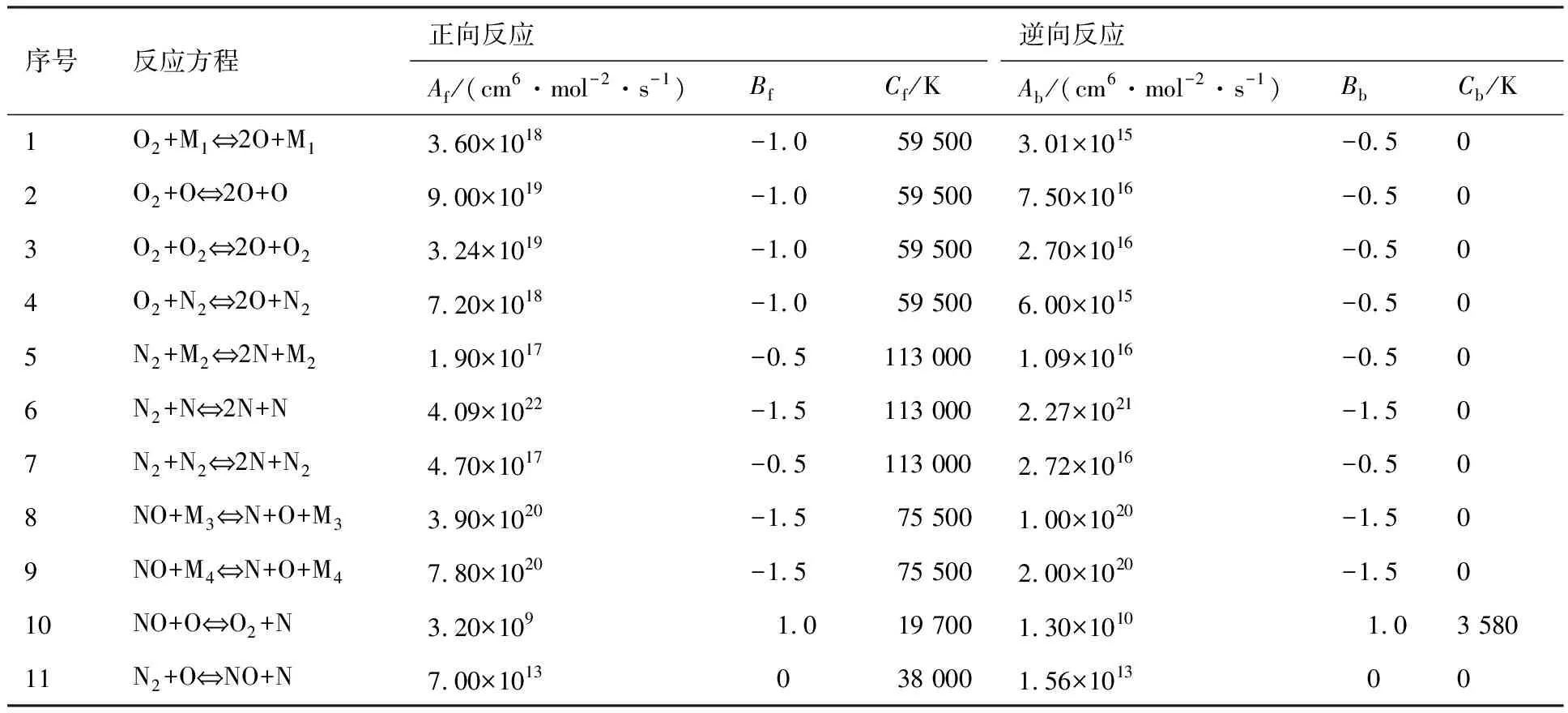
表1 5组元空气反应Dunn&Kang模型[5]Table 1 Dunn&Kang model for 5 species air reaction[5]

注：M1=N,NO;M2=O,O2,NO;M3=O2,N2;M4=O,N,NO

式中：W为单元界面重构的流场变量，在本文中取控制方程的原始变量；上标“L”和“R”分别表示变量是自单元界面的左边(left)或右边(right)重构得到；minmod为限制器函数。

高超声速化学非平衡流动的特征时间尺度和化学反应特征时间尺度相差较大，各个化学反应的特征时间尺度也有较大差异，由此带来所谓的“刚性问题”，使得CFD求解收敛困难。目前主要通过3类方法解决“刚性”问题：全隐算法[9]、点隐算法[10]和解耦算法[11]，其中全隐算法将控制方程中的对流项、黏性项和化学反应源项都进行隐式处理，因此时间步长不受稳定性条件限制。从并行计算的角度看，以LU-SGS(Lower-Upper Symmetric Gauss-Seidel)为代表的传统隐式方法具有数据依赖，不适合并行计算，在并行分区数较大时收敛速率下降。全矩阵DPLUR(Full Matrix Data-Parallel Lower-Upper Relaxation)[9]隐格式是一种全隐算法，它采用精确的分裂后的无黏Jacobian矩阵代替LU-SGS等对角化方法中的近似矩阵，避免了对角化近似对实际时间步长的影响；采用精确的源项Jacobian矩阵代替对角化方法中的近似矩阵，能够反映不同化学反应的快慢；采用内迭代松弛过程代替LU-SGS中的扫描过程，消除了相邻网格单元隐式求解中的数据依赖。作为一种收敛速率快、适合于并行计算的隐式方法，全矩阵DPLUR是美国高温非平衡流动CFD软件US3D主要的隐式方法，是美国另一高温非平衡CFD软件DPLR作为补充的隐式方法。

本文采用全矩阵DPLUR方法进行时间推进，计算过程为：在m=1,mmax中开展循环得到

(6)

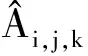
1.2 DSMC方法

DSMC方法是求解稀薄气体流动常用的数值模拟方法，采用大量的仿真分子，在微观水平上模拟分子的运动和碰撞过程，求解真实气体流动过程。不论在模拟热力学非平衡还是化学非平衡方面，DSMC方法均具有很强的能力。本文采用的是Bird的DSMC方法[13]，分子的模拟采用VHS(Variable Hard Sphere)分子模型，分子内部能量交换模拟采用L-B(Larsen-Borgnakke)模型。

在处理化学反应过程中，化学反应模型采用1.1节CFD中相同的模型和数据。化学反应速率系数式(4)改写为

kD(T)=ΛTηexp(-Ea/kBT)

(7)

式中：Ea为单个反应所需的活化能；Λ和η分别与式(4)中的Afr和Bfr意义相同；kB为Boltzmann常数。

高温空气中，一个组元A分子与一个组元B分子发生碰撞，其发生离解或置换反应的概率为

(8)

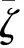
复合反应概率与第三体的数密度nT成正比。通常情况下，如果活化能为零，复合反应的概率为

(9)

1.3 MPC耦合方法

在高超声速流动中，虽然采用CFD技术，能够达到较高的计算效率。但是非平衡流动中，往往会出现Navier-Stokes方程失效的情况。一般采用当地Kn判断Navier-Stokes方程的失效问题，其表达式为

(10)

式中：λ为当地流场气体分子平均自由程；Q为当地流场宏观参数，可以是压力、密度或温度。

该参数同时考虑了当地密度(平均自由程)和流场参数梯度的影响。取梯度最大的流动参数来计算Knl。当Knl≥0.02，认为连续流方程失效。在跨激波区域(特别是强激波)和边界层内，虽然密度较高，但流场梯度较大，容易出现连续流方程失效的情况。尾迹流区域内，由于气流膨胀迅速，而且密度较低，也容易出现稀薄气体效应(参见图1)。

在连续流方程失效的区域，采用DSMC方法能够很好地模拟稀薄气体效应。但是DSMC方法计算效率较低，限制了其应用范围。如果在一个流场中同时包含连续流区域和稀薄气体效应区域，采用两种算法耦合计算，是一个有效的方法。

在一个流场中同时使用CFD和DSMC方法，需要采用一定的耦合方法，把两套软件耦合在一起。本文采用一种称为MPC(Modular Particle-Continuum)的耦合处理技术[31-33]。

MPC的基本思想是把整个流场分为两种区域，CFD区域和DSMC区域。两种方法各自独立计算。在分界面上，两种方法进行信息交换。

MPC耦合技术中，对计算区域划分统一的网格。DSMC方法的计算区域需要根据计算过程中流场参数自动选取，选取那些连续流方程失效的区域。采用式(10)来判断连续流方程是否失效。连续流方程失效的网格，组合成DSMC计算区域，在这些网格内，采用DSMC方法进行模拟。在计算过程中，根据CFD结果不断调整DSMC方法计算区域，直到流场达到稳定。图1绘出按上述方法进行自动调整的流场分区示意图，其中蓝色为Navier-Stokes计算区域，绿色为DSMC计算区域。

耦合计算过程中，两种计算方法需要进行双向信息交换。CFD向DSMC区域信息传递时，在CFD与DSMC方法的分界网格面上，根据CFD计算的当地流场参数，向DSMC区域随机补充仿真分子，仿真分子携带耦合边界的宏观信息。

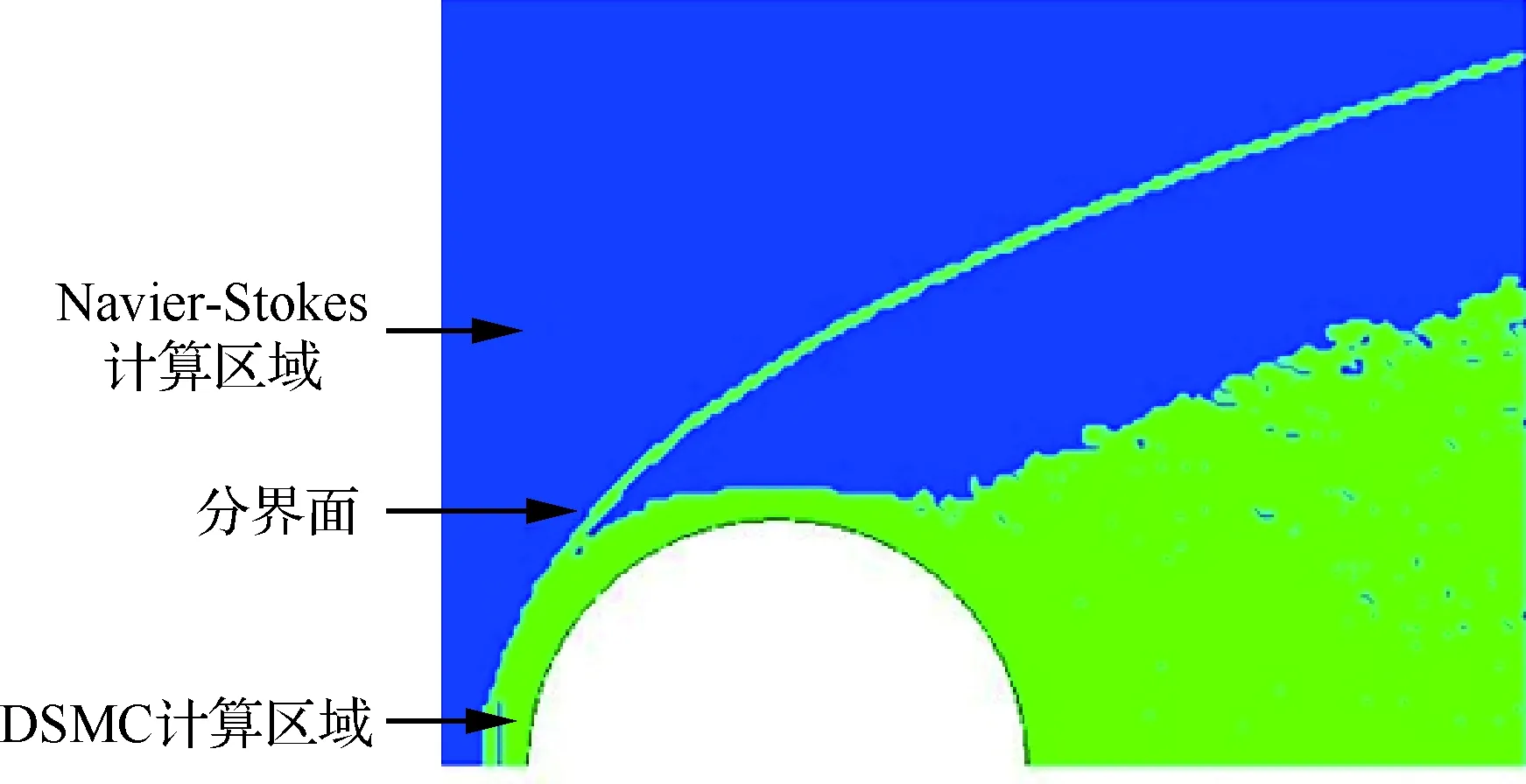
图1 Navier-Stokes/DSMC耦合算法分区示意图Fig.1 Sketch of regions in Navier-Stokes/DSMC hybrid algorithm

根据连续流失效判断方法，当Knl≥0.02时，在耦合边界上，流动已经开始出现非平衡现象，此时速度分布函数已经不再符合Maxwell平衡分布，可以采用Chapman-Enskog分布来描述[41]。

对于偏离Maxwell分布的非平衡分布，其一阶展开形式为

f(C)=f0(C)Γ(C)

(11)

式中：f0为平衡态Maxwell分布函数；C为无量纲化的分子热运动速度矢量，C=c/(2kBT/m′)1/2，c为 分子热运动速度，m′为气体分子质量。Γ(C)表达式为

(12)

其中：C为分子速度，下标x、y、z为3个坐标方向；q为热流；τ为剪切应力项；xi为i方向的坐标；κ为热传导系数；μ为黏性系数；δij为Kronecker符号(当i=j时，δij=1，当i≠j，δij=0)；u、v、w为3个方向的流动速度；p为压力。

本文采用文献[41]给出的方法，在边界面上给出符合Chapman-Enskog分布的分子速度。该方法基于Maxwell分布的速度采样方法，根据当地的非平衡度，采用“拒绝-接受”的随机步骤，产生符合Chapman-Enskog分布的分子速度。

DSMC向CFD区域进行信息传递时，由于DSMC方法的结果有一定的统计波动，在化学非平衡的流场中，在某些区域，部分组元的含量很少，统计波动很大。DSMC统计波动如果传递到CFD求解区域，可能会导致CFD求解不稳定。为了克服这一困难，本文采用了一种称为“亚松弛”的技术来抑制DSMC方法的统计波动对CFD计算的影响。

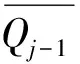
(13)

式中：θ为网格中新参数比较小的权重；相应地，1-θ为比较大的权重。

在本文的CFD计算中，采用的是单温度模型，在DSMC结果向CFD传递信息时，把移动温度、转动温度和振动温度按自由度加权平均，作为一个温度传递给CFD计算。

仿真实践表明，这种“亚松弛”技术，能够比较好地抑制DSMC方法的统计波动对CFD计算的影响。特别是化学非平衡流场中，含量较低的组元的统计波动，也能够得到很好的抑制。

耦合方法的计算步骤为

步骤1计算区域划分统一的网格。为了加快计算进度，本文在边界层内预设nD层网格为DSMC计算区域(nD可调)，其余为CFD计算区域。为各计算区域设置边界条件和初始条件。

步骤2进行CFD和DSMC独立计算。为了尽量保持CFD和DSMC计算的同步，本文设置DSMC每计算mD步进行1步CFD计算(mD可调)。

步骤3信息交换。每进行1步CFD计算，开展一次信息交换。耦合边界上，DSMC根据CFD结果改变边界信息，CFD根据DSMC结果采用亚松弛改变相应网格点上的宏观参数。

步骤4每隔kD个时间步长(kD可调)调整一次DSMC计算区域。根据CFD结果，采用当地克努森数判断连续流方程的失效网格，标注为DSMC计算的网格。

步骤5重复步骤2～步骤4，直到流场稳定。

步骤6流场稳定后，不再进行分区调整，继续重复步骤2～步骤3，直到DSMC统计到足够的样本。

2 算例结果与讨论

2.1 二维圆柱高超声速化学非平衡绕流

分别采用全DSMC和Navier-Stokes/DSMC耦合方法计算了空气5组元(N2、O2、NO、N、O)的化学非平衡流场。计算模型为二维圆柱。计算条件与文献[17]一致。来流参数：速度U∞=7 810 m/s， 温度T∞=178.2 K，Kn∞=0.01，来流组元(N2、O2、O)的摩尔分数分别为0.775、0.204、0.021，壁面温度Tw=1 000 K。

本算例中，在采用相同的仿真粒子密度的条件下，均用24进程并行计算，全DSMC和Navier-Stokes/DSMC计算时间之比约为2.4:1，表明耦合算法比全DSMC计算能提高计算效率。

图2是采用全CFD和耦合算法时两种残差曲线的对比。采用全CFD计算时，残差降低迅速，很快能下降4个量级，说明本文采用的方法能够解决化学反应的刚性问题。在耦合算法中，CFD的残差降低较慢，有两个原因：① 为了能够尽量和DSMC计算保持同步，计算中采用了较小的CFL(Courant-Friedrichs-Levy)数(DSMC计算中采用的是真实的时间)，而且DSMC计算两步，CFD计算一步；② 受DSMC统计波动影响，CFD残差也有一定波动，而且在流场稳定后，残差与初始计算相比也下降3个量级后不再变化，说明耦合计算中CFD部分已经收敛。

图3是耦合算法和全DSMC计算得到的移动温度(Ttr)场云图。对比两种结果，可以看出，在空间分布上，两种结果基本一致。图4是驻点线上N2移动温度和振动温度(Tvib)的比较。在驻点线上，耦合算法的结果中，由于引入了CFD的计算，移动温度激波的起始位置稍微落后于全DSMC的结果，激波厚度更薄。振动温度与全DSMC的结果基本一致，而且与文献[17]结果也比较吻合。虽然在本文的CFD算法中，所采用的热力学模型为热力学平衡模型，但在热力学非平衡的计算中，在误差许可范围内，可以得到与全DSMC一致的结果。

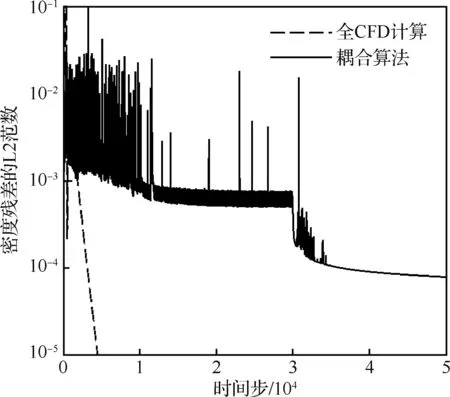
图2 CFD残差曲线对比Fig.2 Comparison of CFD residual curves

图5是驻点线上数密度(n)和压力(p)分布。比较表明，两种结果的数密度和压力在驻点线上分布吻合较好，激波起始位置和波后参数基本一致。在驻点处，耦合算法的数密度比全DSMC结果稍高。

图6是两种算法结果中组元O摩尔分数的分布云图。在激波后，由于气体温度很高，O2的离解度较高。从图7中给出的驻点线上各组元的摩尔分数(fmole)分布图中可以看出，波后O2的摩尔分数很低，接近为0，说明O2基本上全部离解。N2的离解度也很高，3种结果中(文献[17]、全DSMC、耦合算法)波后N2摩尔分数的最小值分别为0.238、0.212、0.198，耦合算法的结果中，N2的离解度更高一些。相应地，波后N的摩尔分数耦合算法结果更高。比较表明，两种算法给出了基本一致的结果，与文献的结果吻合很好。

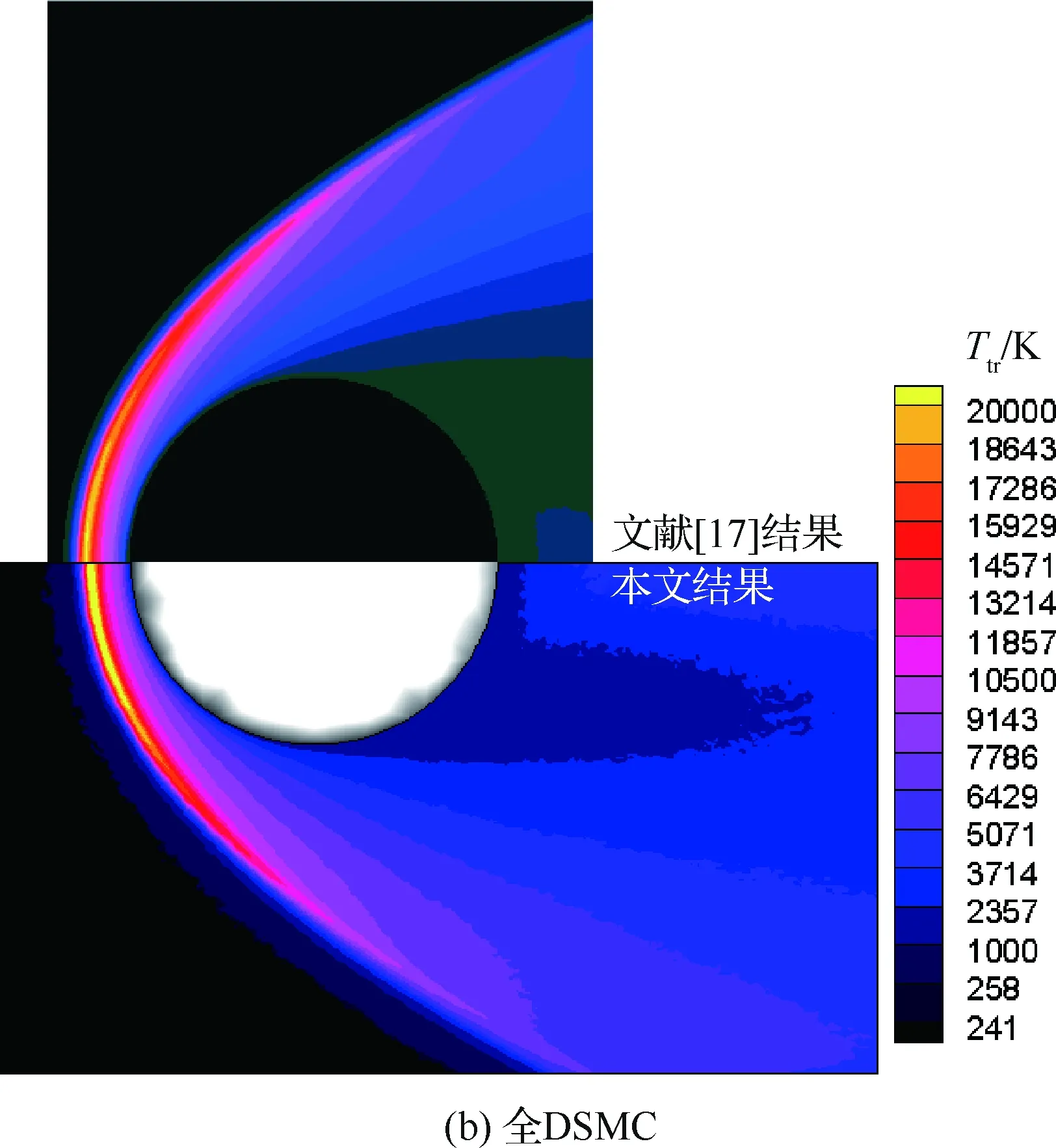
图3 流场移动温度分布Fig.3 Distribution of translational temperature in flow field

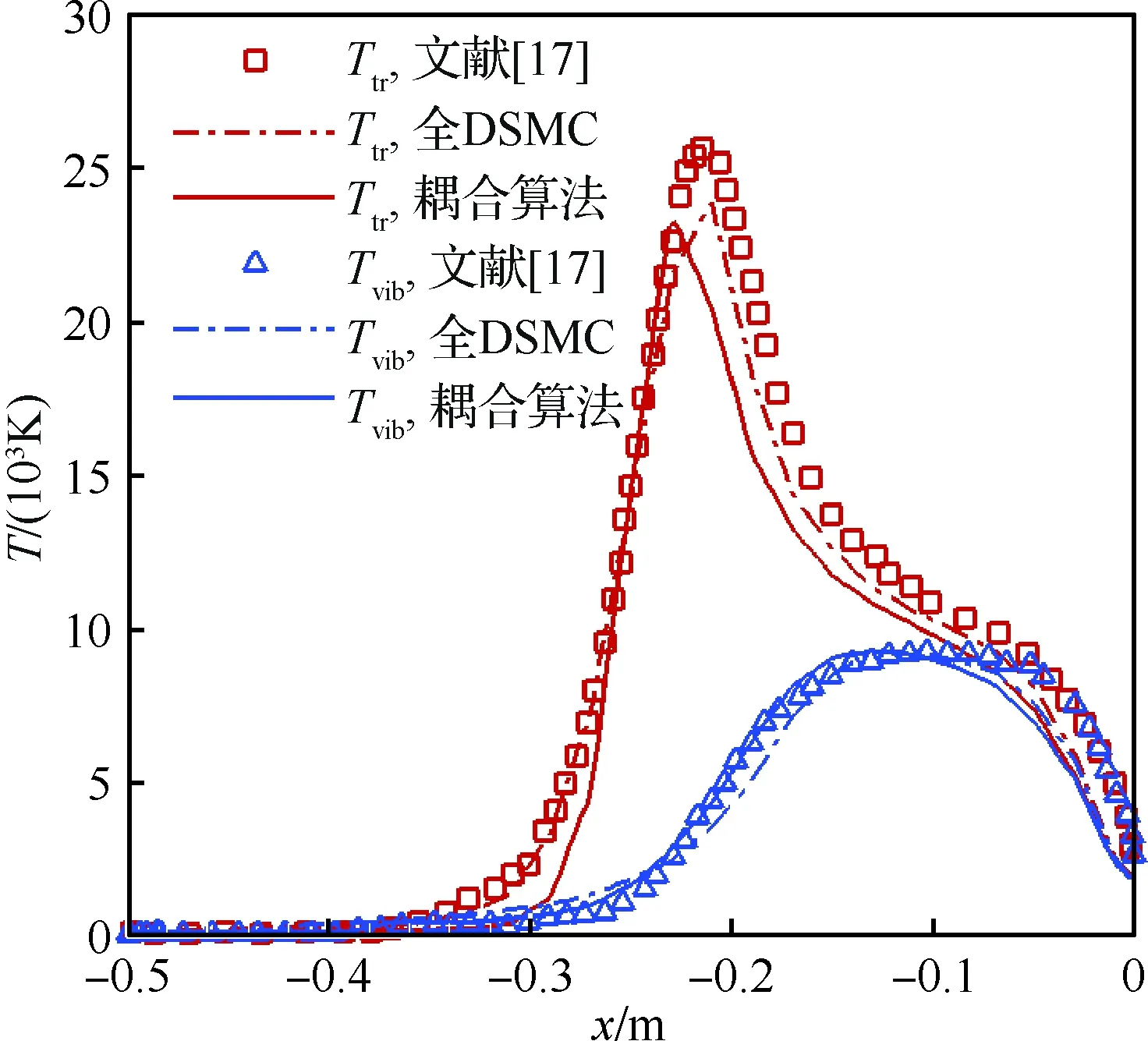
图4 驻点线温度分布比较(N2)Fig.4 Comparison of temperatures distribution on stagnation streamline (N2)

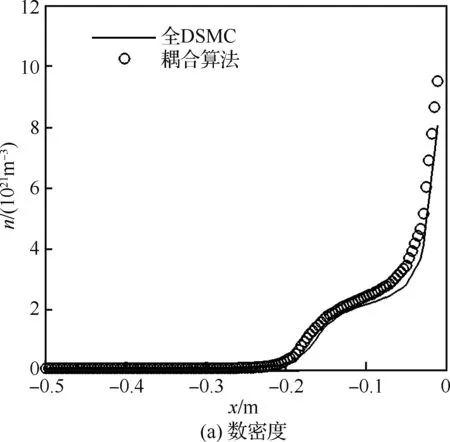
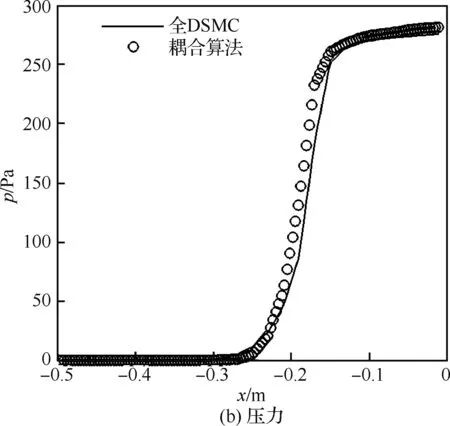
图5 驻点线参数分布比较Fig.5 Comparison of parameter distribution on stagnation streamline

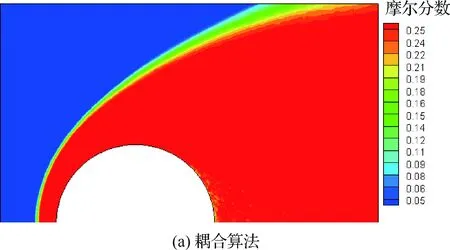
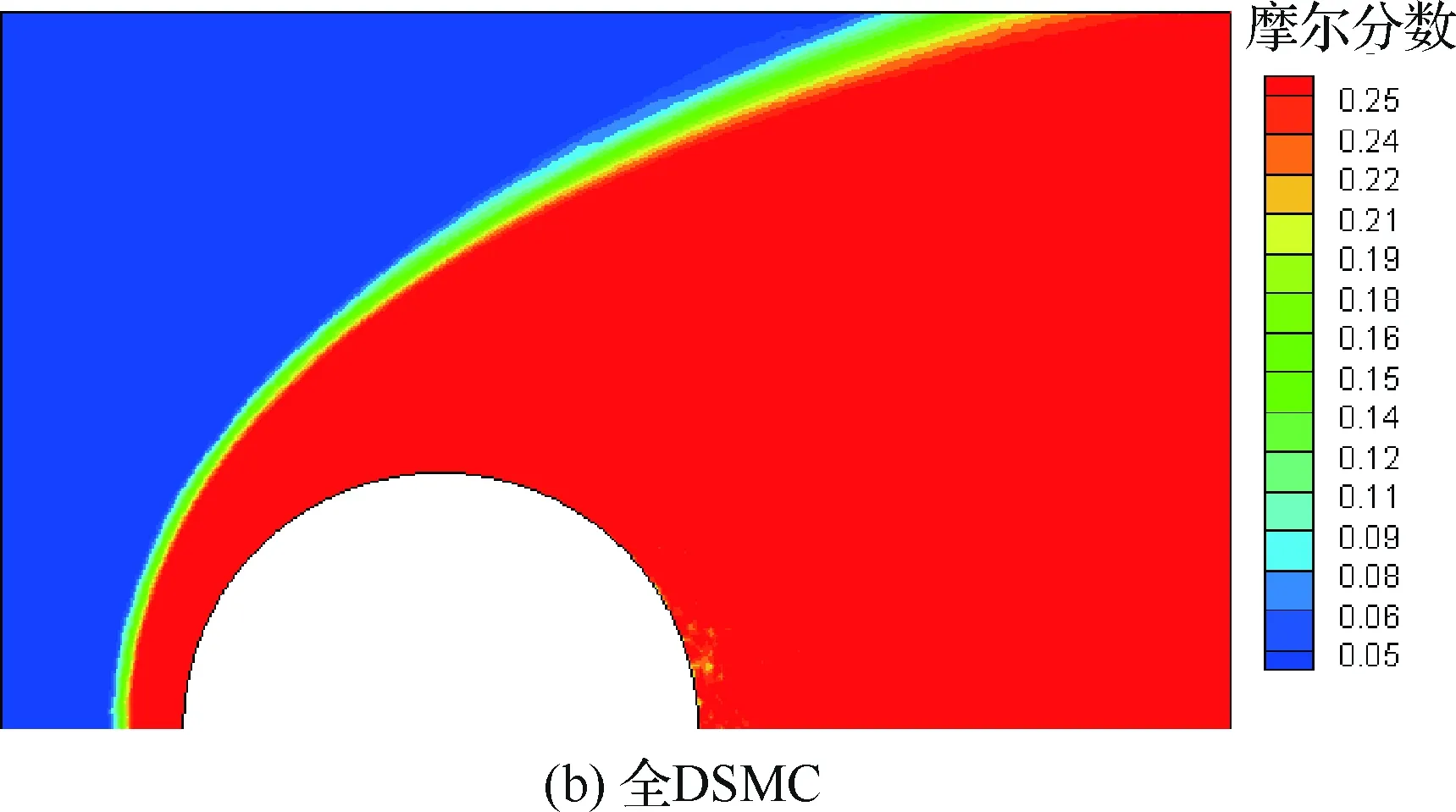
图6 O摩尔分数分布Fig.6 Distribution of O mole fraction

图7 驻点线组元摩尔分数分布比较Fig.7 Comparison of species mole fraction distribution on stagnation streamline

以上比较表明，在化学非平衡的模拟方面，耦合算法能够得到与全DSMC模拟较为一致的结果。

图8是圆柱表面压力和热流的比较。对于表面压力p，全DSMC与耦合算法的结果基本重合在一起。对于表面热流q，在驻点处，由于耦合算法的数密度稍高(参见图5(a))，热流也比全DSMC结果偏高，其他区域两种结果符合很好。

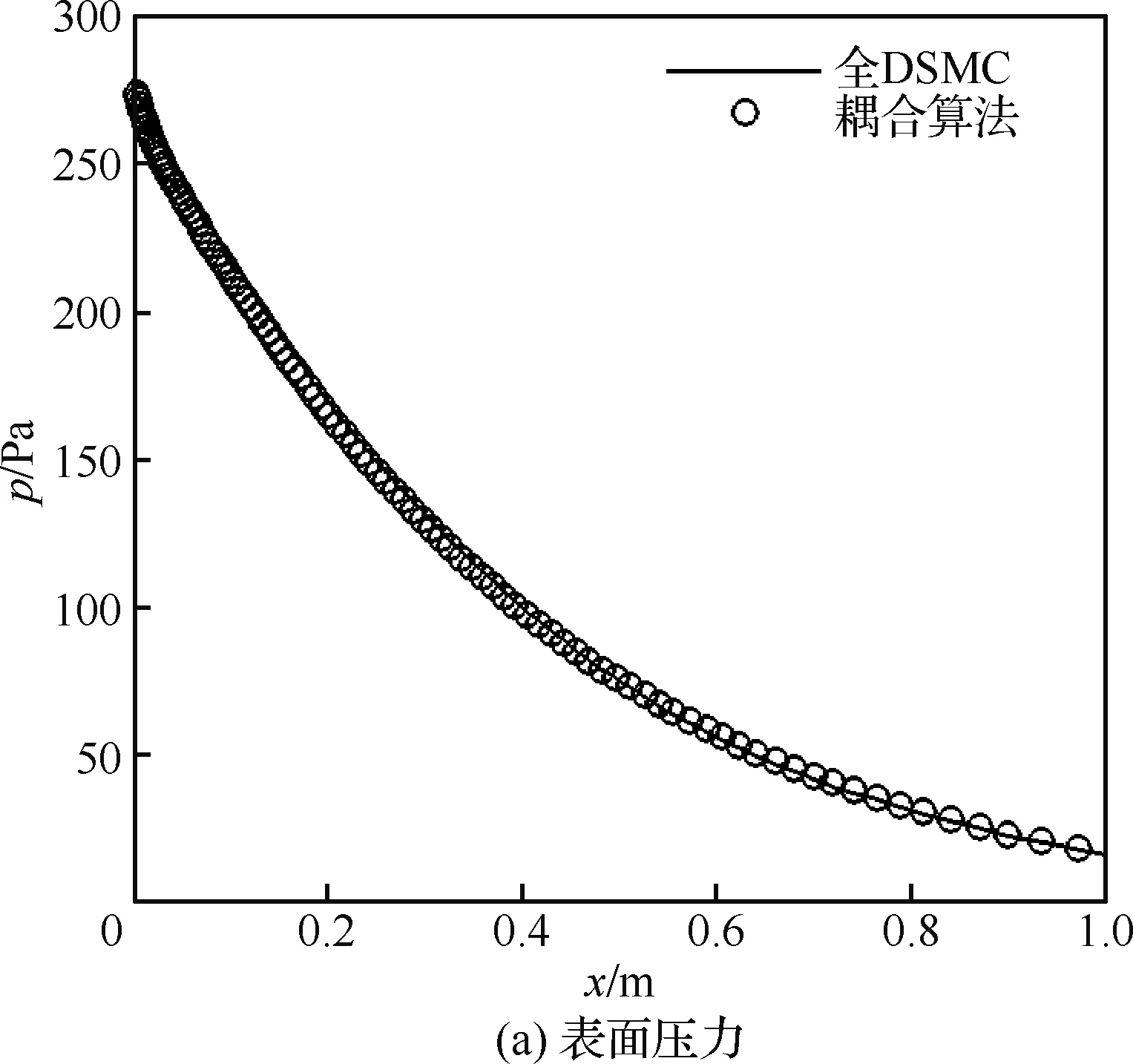
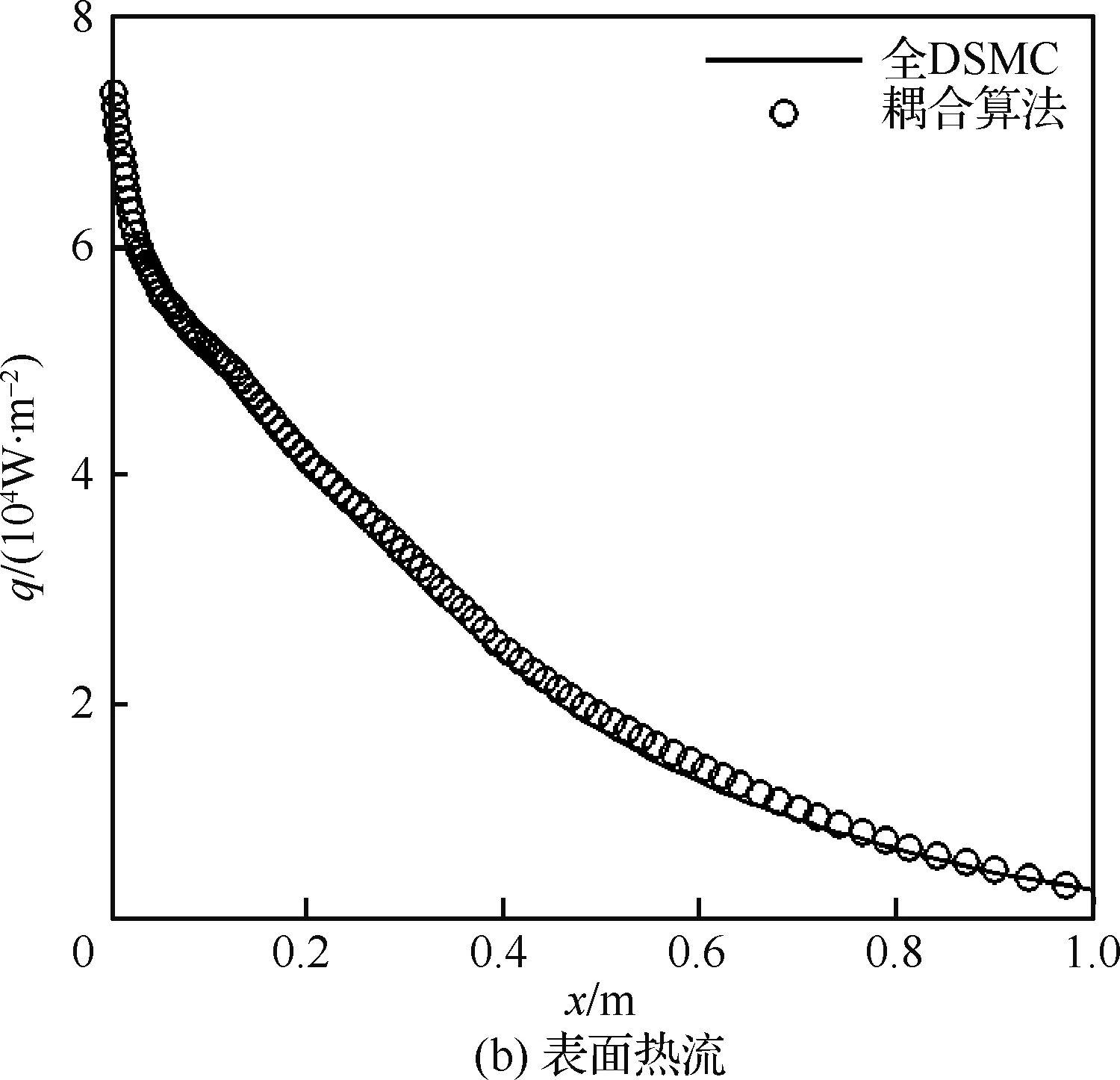
图8 壁面参数分布比较Fig.8 Comparison of surface parameters distribution

在整体气动力、热特性方面，对于圆柱的阻力系数CD，全DSMC和耦合算法的计算结果分别为：CD_DSMC=1.33，CD_Hybrid=1.34，比文献[17]的结果CD_Ref=1.32分别高0.75%和1.51%。对于热流系数Ch，全DSMC和耦合算法的结果分别为：Ch_DSMC=0.059，Ch_Hybrid=0.056，比文献[17]的结果Ch_Ref=0.062分别低4.8%和9.6%。结果表明，耦合算法与全DSMC方法对整体气动力、热特性的模拟比较接近。

2.2 航天器碎片过渡区绕流耦合计算

采用所建立的耦合算法，对某航天器解体碎片在过渡区的化学非平衡绕流开展了计算。解体碎片简化为球柱模型，模型长度为1.3 m，直径为0.246 m。模拟参数见表2，迎角为0°。

图9是不同高度上(H=80、70 km)流场压力分布。可以看出，随着高度降低，激波脱体距离逐渐减小。图10是典型的表面压力和热流分布，在这种外形简化条件下，最大压力和热流均出现在驻点区域。

图11是驻点线上N、O的质量分数(fmass)分布。随着高度降低，激波脱体距离减小，N2、O2开始离解的位置向后移动。对于O原子，其质量分数最大值差别不大。对于N原子，随着高度的降低，质量分数增大，表明在计算范围内，高度降低，化学反应越来越强烈。

图12是轴向力系数Ca和驻点热流q0随高度的变化。随着高度降低，Ca减小。在85～75 km 范围内，Ca降幅较大，在75～70 km范围内，Ca降幅较缓。随着高度降低，q0大幅升高。

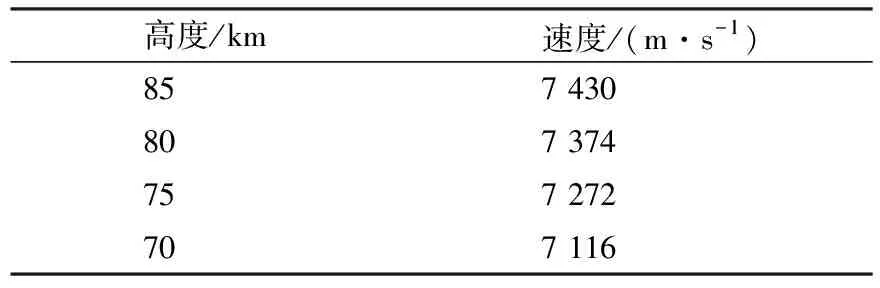
表2 碎片模拟高度和速度Table 2 Altitude and velocity of fragment simulation

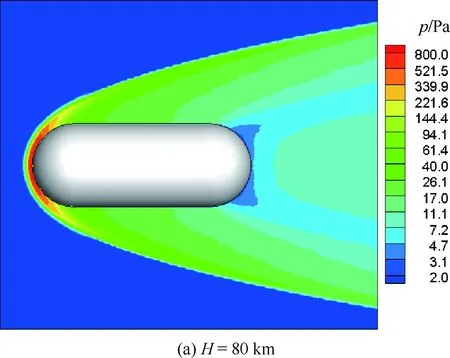
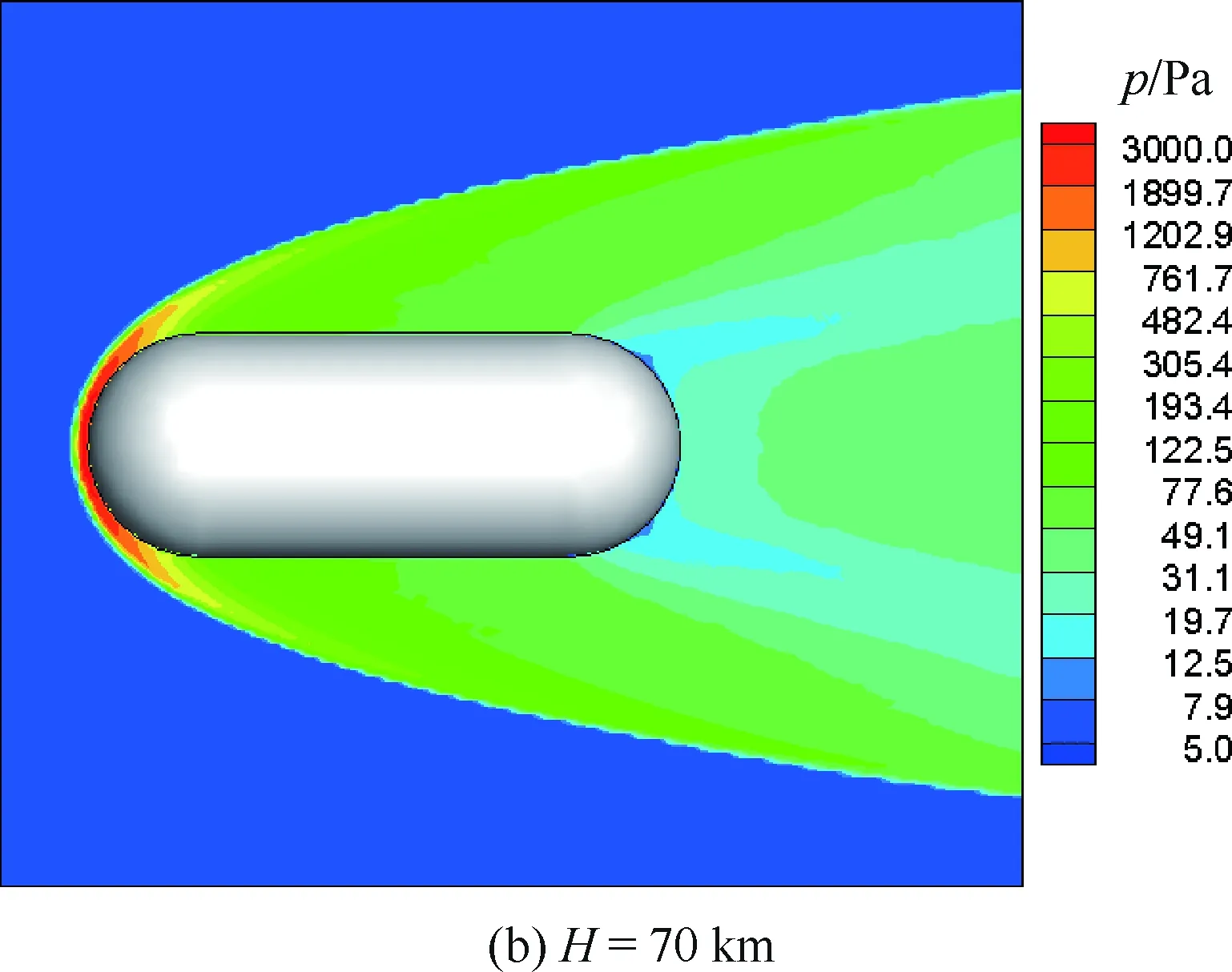
图9 碎片不同高度上的流场压力分布Fig.9 Pressure distribution of flow field of fragment at different altitudes

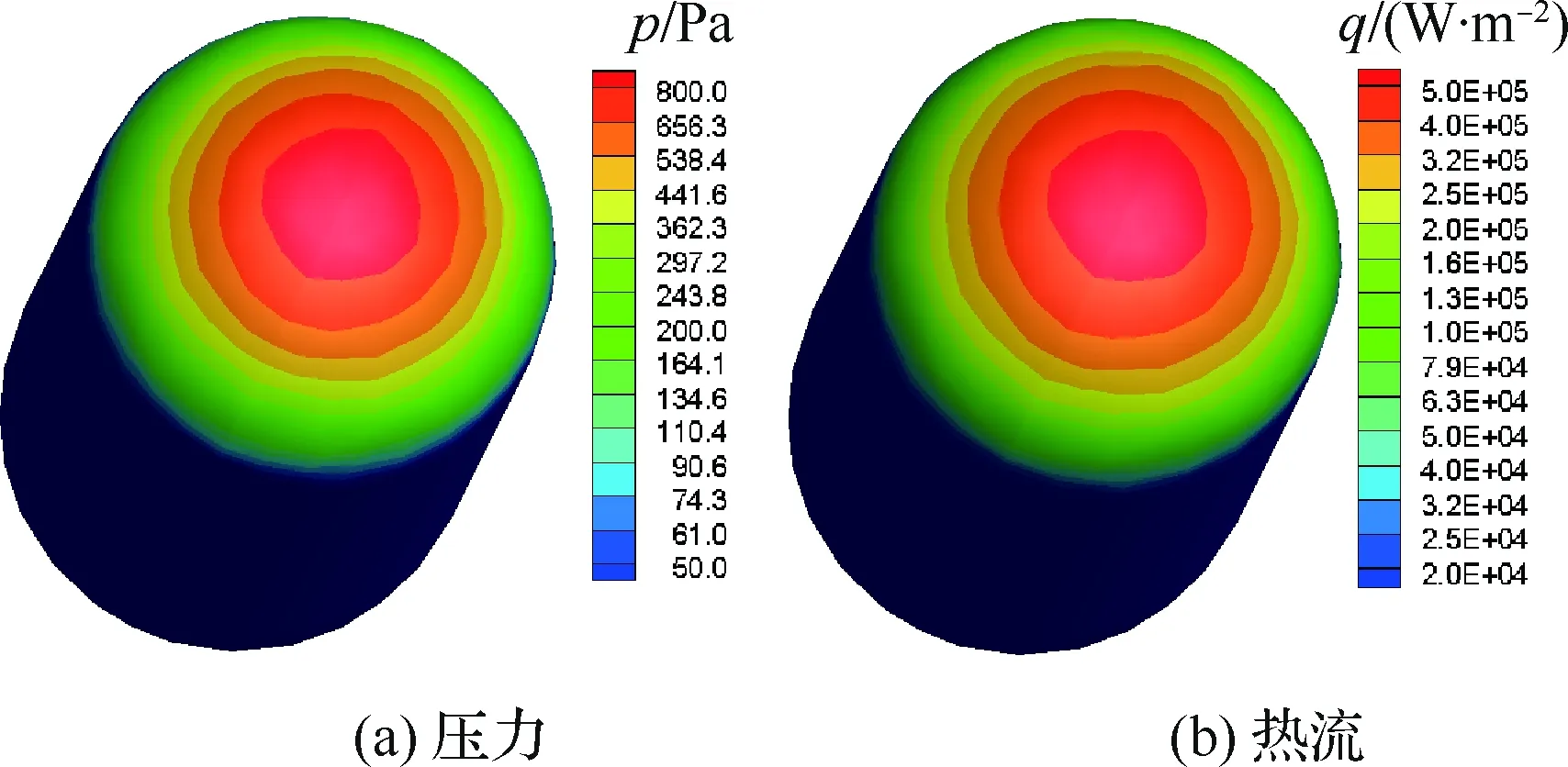
图10 碎片典型表面压力和热流分布Fig.10 Typical distribution of pressure and heating flux on fragment surface

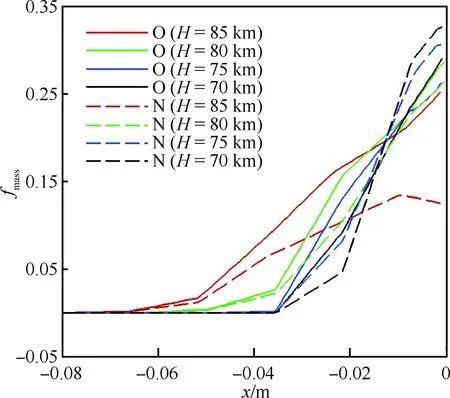
图11 驻点线N、O质量分数分布Fig.11 Distribution of mass fraction of N and O on stagnation streamline

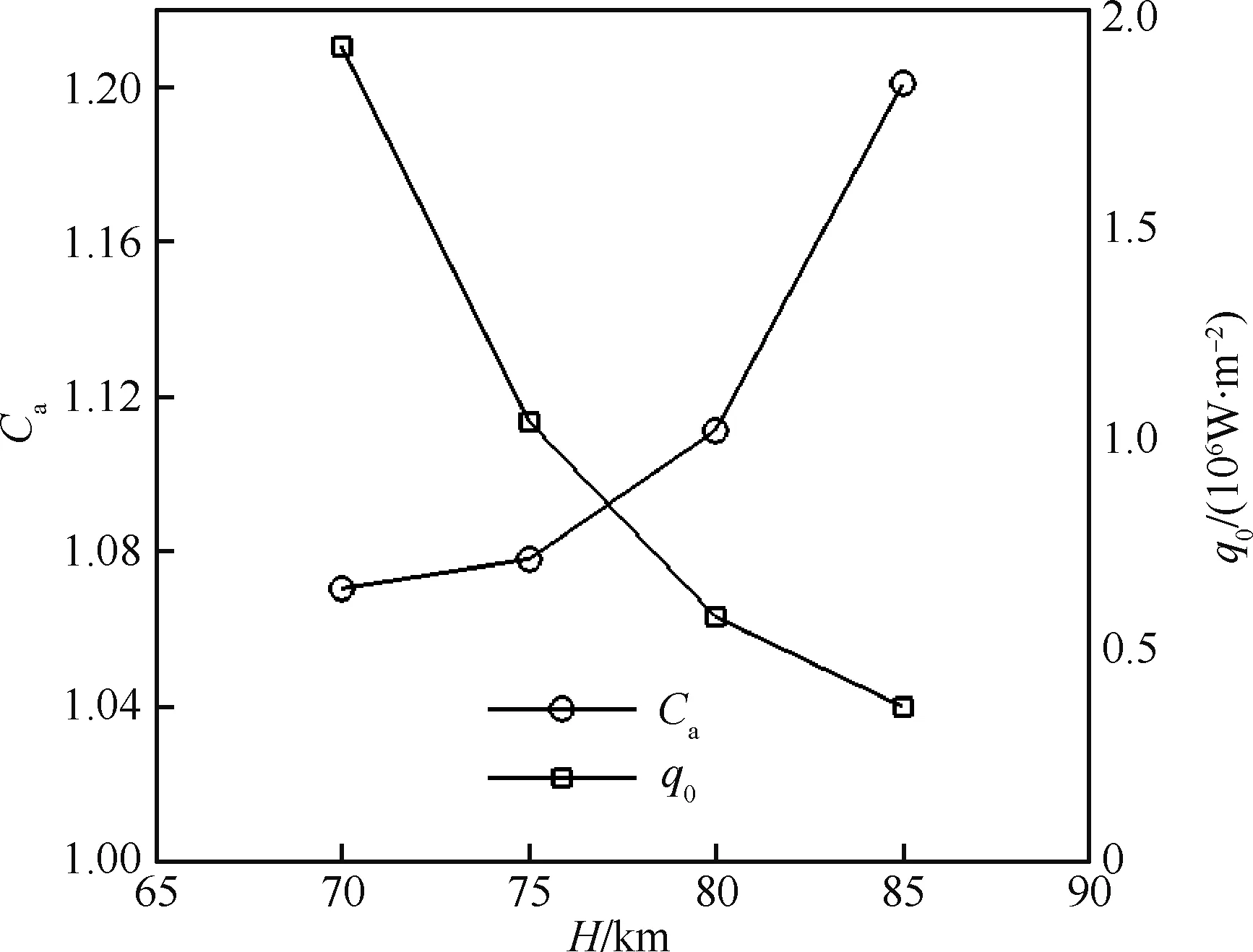
图12 轴向力系数和驻点热流随高度的变化Fig.12 Variation of Ca and q0 with altitude

3 结 论

1) 基于相同的化学反应模型和数据，采用MPC耦合技术，发展了化学非平衡流动的Navier-Stokes/DSMC耦合算法，在近连续过渡流区高超声速绕流模拟中实现了化学非平衡耦合计算。

2) 通过高超声速圆柱绕流的算例与其他结果的比较研究，表明耦合算法不论在流场结构、流场非平衡现象、还是飞行器表面参数、飞行器整体气动力/热特性方面，都能够得到全DSMC计算吻合的结果，证实本文设计的耦合方法是可行的。

3) 通过对碎片在过渡流区的仿真，得到碎片在过渡流区的力/热特性。在过渡区，轴向力系数随高度下降而减小，驻点热流随高度降低而大幅增加。

本文的CFD算法中，所采用的热力学模型为单温度模型，该模型假设气体处于热力学平衡状态。而DSMC方法是热非平衡的模型，在耦合的过程中会出现一定的偏差。对于更精确的耦合算法，需要开展热力学非平衡的CFD技术和相应的耦合技术研究。