变转速旋翼直升机单发失效低速回避区分析

严旭飞，池骋，陈仁良，李攀

南京航空航天大学 直升机旋翼动力学国家级重点实验室，南京 210016

出于对桨毂振动、系统复杂程度、发动机及传动技术等问题的考虑，目前绝大多数直升机的旋翼都以固定转速工作，因此只能使旋翼在一定的飞行条件下处于效能最优状态。事实上，依据当前飞行速度、重量、飞行高度等参数适当改变旋翼转速，可以在整个飞行过程中实现最小化旋翼需用功率，从而大幅提高续航能力。

近年来，随着材料技术、发动机技术与传动技术的发展，变转速旋翼(Variable Speed Rotor, VSR)已经可以实现，并被应用到一些先进的旋翼飞行器上，以提高飞行性能。如A160蜂鸟长航时无人直升机、X2共轴刚性旋翼高速直升机、XV-15和V-22倾转旋翼机等[1]。同时，越来越多的人从旋翼需用功率、航程航时[2-4]、振动载荷、旋翼噪声[5-6]和操纵性[7-8]等方面进行变转速旋翼直升机的设计和研究，以进一步提高直升机的各项飞行性能。

以上这些研究尚未考虑到旋翼转速变化对直升机单发失效自转着陆性能的影响。自转着陆是直升机单发失效后安全着陆的唯一手段，因此自转着陆性能也是直升机设计的一个重要指标。而旋翼转速的变化会改变旋翼当前储存的动能，进而影响到直升机的自转着陆性能。对于具有两台或者多台发动机的运输类直升机来说，当遭遇单发失效时，剩余发动机仍能输出可用功率。如果能找到一个合适的旋翼转速范围，既可以减小旋翼的需用功率与剩余可用功率之间的差距，又可以保证旋翼具有足够的动能进行自转着陆，则该旋翼转速不仅能有效降低直升机的需用功率，还有利于提高直升机单发失效后的自转着陆性能。因此，本文主要研究变转速旋翼对多发运输类直升机单发失效后自转着陆性能的影响。

直升机的单发失效自转着陆性能可以通过回避区来直观反映[9-10]。回避区显示了驾驶员在正常操作期间的不安全区域(一般在低速范围)，在该区域内如果出现单发失效，即使是最熟练的驾驶员也无法安全地进行自转着陆。因此，回避区的范围越小，说明直升机的自转着陆性能越好；反之则说明直升机的自转着陆性能越差。对于给定的飞行环境和直升机重量，回避区一般由发动机失效时直升机的高度和速度组合来描述，即高度-速度(Height-Velocity, H-V)曲线[10]。飞行试验是确定H-V曲线的最终手段，但其风险较高，且耗时耗资。为了降低飞行试验的成本和风险，近年来一般采用最优控制方法来预测直升机的H-V曲线以及相应的飞行轨迹和操纵过程[11-12]，为飞行试验提供理论依据[13-14]。

本文主要利用最优控制方法研究变转速旋翼直升机在遭遇单发失效时，不同旋翼转速对自转着陆低速回避区的影响。此外，由于直升机的航时、航程和升限等大部分性能指标主要与直升机的需用功率相关[1-4]，故本文还研究了低速范围内旋翼转速对直升机需用功率的影响，并将两种影响进行对比。除了操纵行程限制之外，本文对旋翼转速变化无其他附加条件限制。事实上，旋翼转速的变化还会影响到桨毂振动水平和气动噪声等，在工程应用中应综合考虑，本文在计算分析时暂时不考虑这些因素。

首先以UH-60A直升机为样机，建立三维刚体飞行动力学模型，并分析低速范围内旋翼转速变化对直升机需用功率的影响。然后，在飞行动力学模型中加入单发失效后自转着陆阶段的发动机输出功率和旋翼转速变化方程[12]，并使用操纵杆量的一阶导数作为控制量，将直升机单发失效后的自转着陆过程转换为非线性最优控制问题进行求解。最后，基于最小化回避区面积的思想，研究直升机在不同旋翼转速下遭遇单发失效后的自转着陆低速回避区变化，以及各旋翼转速下回避区的高悬停点、拐点和低悬停点的最优着陆轨迹和操纵过程，并将最小回避区对应的旋翼转速与最小需用功率对应的旋翼转速进行对比分析。

1 飞行动力学模型

以UH-60A直升机为样机，首先建立常规直升机的三维刚体飞行动力学模型(模型建立和验证过程详见文献[15]，这里只作简单描述)。其中旋翼模型采用叶素理论，桨叶剖面的气动力系数由翼型风洞试验数据给出，桨叶挥舞运动由挥舞刚性二阶动力学模型来描述；旋翼诱导速度采用Pitt-Peters一阶动态入流模型，并考虑地面效应和涡环状态边界；尾桨的气动力模型与旋翼相似，采用叶素理论计算气动力，诱导速度采用均匀入流模型计算，同时考虑旋翼和机身对尾桨的气动干扰、涡环边界以及垂尾对尾桨的阻塞效应；机身、平尾与垂尾的气动力和气动力矩系数采用风洞试验数据插值的方式得到，并计入旋翼尾迹和机身对平尾、垂尾的气动干扰。模型的状态空间形式可以表示为

(1)

通过配平方程式(1)，可以研究直升机稳态飞行时，旋翼转速变化对直升机需用功率的影响，对应的计算和分析结果见4.1节。

假设直升机在单发失效前处于稳定前飞或者悬停状态。遭遇单发失效后，驾驶员操纵直升机进入自转着陆过程，则单发失效后发动机的输出功率变化以及旋翼转速变化可以表示为[12]

(2)

式中：PA为发动机输出功率；POEI为剩余发动机最大可用功率；tp为响应时间常数；Ω为旋翼转速；PMR为旋翼需用功率；PTR为尾桨需用功率；k为旋翼转速与尾桨转速的比例因子；η为直升机传动效率因子；IMR为旋翼转动惯量；ITR为尾桨转动惯量。

为了避免在轨迹优化过程中操纵量出现跳跃或者不连续的现象，并考虑到操纵系统特性和驾驶员操纵速率的限制，将操纵量ub对时间的一阶导数(uc,ulat,ulon,up)作为模型控制变量，并把(δc,δlat,δlon,δp)作为模型状态变量的一部分[12]，即

(3)

式(1)～式(3)共同构成了适用于计算直升机单发失效后轨迹优化的三维刚体飞行动力学模型。其微分方程形式可表示为

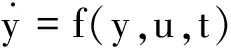
(4)

式中：

(5)

2 问题建立与求解

2.1 回避区

利用最优控制方法和最小化回避区面积的思想计算H-V曲线[9-10]，其主要思路为：在可实现安全自转着陆的条件下最小化回避区面积。在给定的飞行环境和直升机重量下，为求任意高度h0(本文将回避区的高度h定义为UH-60A直升机轮胎底面距离地面的高度)下的回避区边界点(即对应的前飞速度V0)，首先选择一个最小初始速度(一般为0 m/s)，然后逐步增加速度来计算单发失效后的最优自转着陆过程，直到增加至某一速度时，对应的自转着陆过程可实现且令人满意，则此高度和速度的组合即为该高度下的回避区边界点。由上述边界点组成的曲线即为H-V曲线，如图1所示。H-V曲线存在3个重要的边界点，即高悬停点(High Hover Point)，拐点(Knee Point)和低悬停点(Low Hover Point)。这3个点将低速H-V曲线分为上下两个边界。其中上边界以下表示直升机进入自转着陆过程后，无法满足安全着陆的要求；下边界以下表示直升机直接着陆，但由于高度很低，驾驶员可以通过适当的操纵使过载保持在设计载荷范围内。H-V曲线是直升机自转着陆的极限包线，所以单发失效回避区的H-V曲线的范围可以直观反映直升机遭遇单发失效后的自转着陆性能。

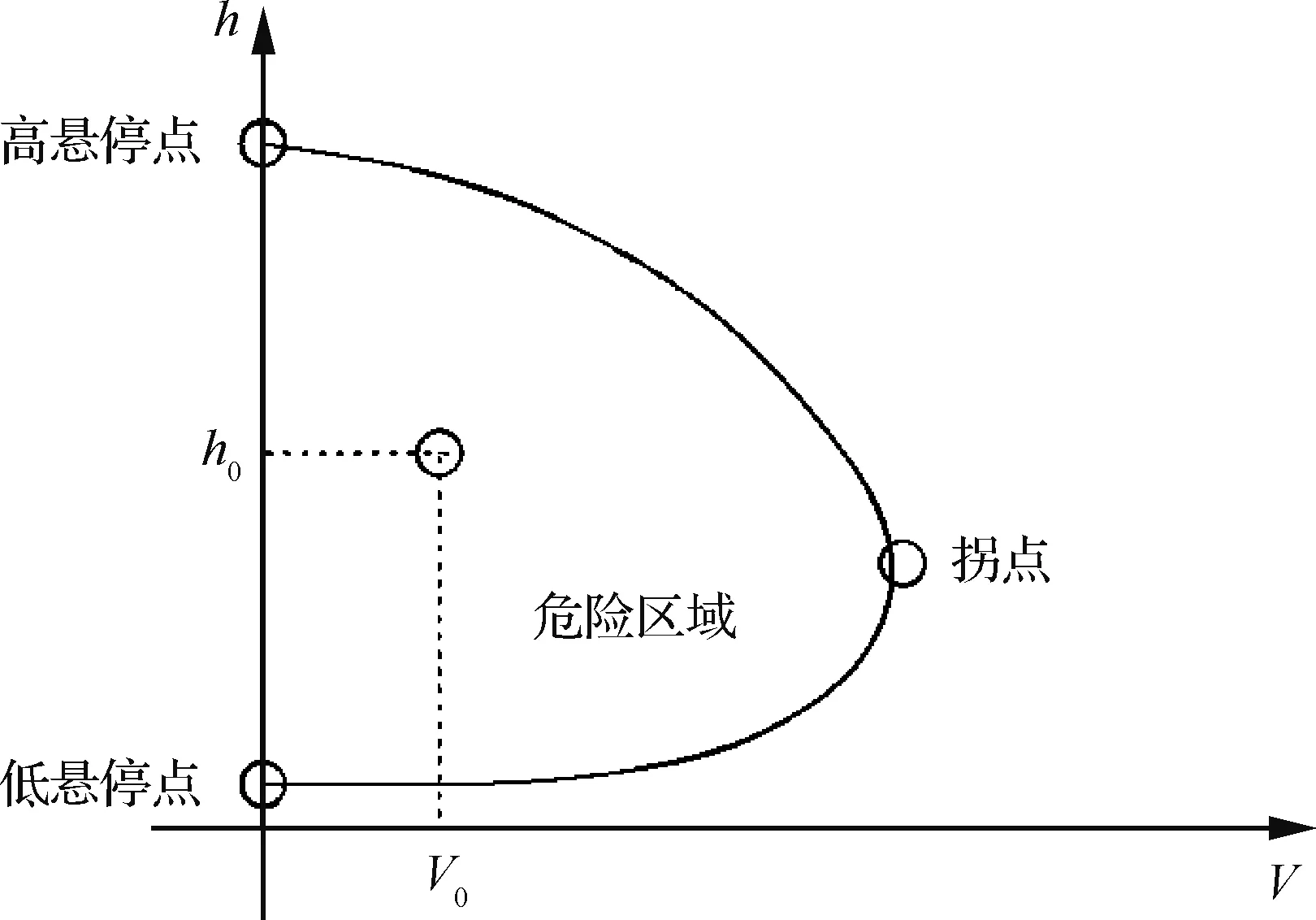
图1 低速状态高度-速度曲线Fig.1 High-velocity curve in low-speed state

2.2 非线性最优控制问题

预测H-V曲线方法的核心在于计算最优自转着陆过程。直升机单发失效后的最优自转着陆过程可以被描述为一种含有状态量和控制量约束的非线性最优控制问题[12]。该问题一般由优化变量、性能指标和约束方程构成。其中优化变量即为模型式(4)中的状态量y和控制量u，以及驾驶员进行自转着陆过程的初始时刻t0和结束时刻tf。性能指标和约束方程的选择如下所述。

2.2.1 性能指标

直升机单发失效后的最优自转着陆过程需要考虑到很多因素。整个过程不仅要保证飞行安全和驾驶员的可操纵性，还需要考虑到时间、驾驶员操纵负荷以及姿态角的稳定性等。此外，还应该最小化直升机着陆时的前飞速度和下降率。本文选择的性能指标为

minJ=wttf+wuUg(tf)+wwWg(tf)+

(6)

式中：

(7)

其中：Ug和Wg分别为地轴系下的前飞速度和下降率；uc,max、ulat,max、ulon,max及up,max为驾驶员杆量的最大操纵速率；φ和ψ分别为滚转角和偏航角；φmax和ψmax分别为自转着陆过程中限制的最大滚转角和偏航角；wt、wu、ww、w1～w6为常数权重因子。

2.2.2 约束方程

约束方程由微分方程、初始边界条件、路径约束和末端边界条件组成。其中微分方程为飞行动力学模型式(4)，其他约束方程包括：

1) 初始边界条件(t0时刻)

根据旋翼飞行器适航管理条例规定[16]，假设直升机在单发失效时，驾驶员延迟1 s后开始操纵直升机(即t0=1 s)。为此，首先根据当前飞行状态对主控方程式(1)进行配平计算，然后通过积分求解微分方程(4)在延迟时间内的自由响应，最后得到初始边界条件[12]为

y(t0)=ydelay，u(t0)=udelay

(8)

2) 路径约束

根据适航管理条例、飞行任务和驾驶员操纵速率约束来确定路径约束，可表示为

(9)

式中：ymin、ymax和umin、umax分别为飞行过程中状态量和控制量的最小值和最大值。

3) 末端边界条件(tf时刻)

根据适航管理条例关于自转着陆的规定即可确定末端边界条件，可表示为

yf,min≤y(tf)≤yf,max

(10)

式中：yf,min和yf,max分别为末端状态量的最小值和最大值。

2.3 数值解法

目前求解复杂非线性最优控制问题最有效的方法，是通过直接方法将该问题转换为非线性规划(NLP)问题，然后采用序列二次规划(SQP)方法进行求解[17]。本文采用直接方法中的直接多重打靶法来完成这一转换过程。直接多重打靶法通常用于转换具有大量自由度以及中等或高复杂性的最优控制问题[18-19]，因此适用于转换本文建立的最优控制问题。

为了防止由于优化变量之间数量级相差较大而造成的数值求解困难，首先对飞行动力学模型式(4)进行无量纲缩放处理(具体过程详见文献[12])。无量纲缩放后的飞行动力学模型可表示为

(11)

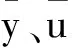
图2为直接多重打靶法的基本原理示意图。如图2所示，首先将时间的无量纲τ平均离散为N-1个时间打靶段：

(12)

在每个离散时间节点处，形成离散的状态和控制参数，则优化变量可表示为

(13)

在第k个打靶段上，以时间步进的方式从τk～τk+1对微分方程式(4) 进行积分，可以得到

(14)

式中:

(15)

采用同样的方式对性能指标进行离散：

图2 直接多重打靶法Fig.2 Direct multiple shooting method

(16)

将路径约束作用在各个时间打靶段节点上，得到

(17)

将边界条件作用在初始和末端时间节点上，得到

(18)

将最优控制问题转换为非线性规划问题之后，应用具有良好鲁棒性的序列二次规划算法[20]进行求解，最后通过插值逼近的方法计算得到原最优控制问题的近似最优解。本文先对每一个时间打靶段上的离散控制量进行线性插值来逼近连续的最优控制过程，然后以时间步进的方式从t0～tf积分状态方程式(4)来逼近最优控制问题的连续最优状态过程。

3 最优控制方法验证

本节采用UH-60A直升机模拟单发失效后自转着陆的飞行试验数据[21]进一步验证本文建立的最优控制方法的可行性和准确性。

本文所用样机型号和飞行试验[21]一致，直升机的飞行任务如下：质量为7 239 kg，处于悬停状态，标准大气环境，高度为9.1 m。随后驾驶员关闭单台发动机模拟单发失效，在延迟1.2 s以后开始进入自转着陆过程。

末端约束根据旋翼飞行器适航管理条例关于自转着陆的要求确定为

(19)

(20)

式中：u、v、w分别为直升机体轴系下的3个速度；ycg为直升机质心的侧向位移；xcg为直升机质心的前向位移。性能指标中的权重系数为：wt=0.01,wu=0.03,ww=0.03,w1=w2=w3=w4=0.15,w5=w6=0.12。

图3为本文计算的单发失效最优自转着陆过程与飞行试验数据的对比，其中nz为垂向过载因子。可以看出，两者吻合较好，且本文计算的总距杆操纵量、垂向过载和俯仰角的变化更加柔和。这是因为在实际试飞过程中，驾驶员的操纵策略不一定是最优的。而最优控制方法可以对操纵速率进行控制和约束，并能根据性能指标寻找最优解，因此可以得到更好的操纵策略和飞行轨迹。通过与飞行试验数据的对比，说明了本文采用的最优控制方法的可行性和准确性。

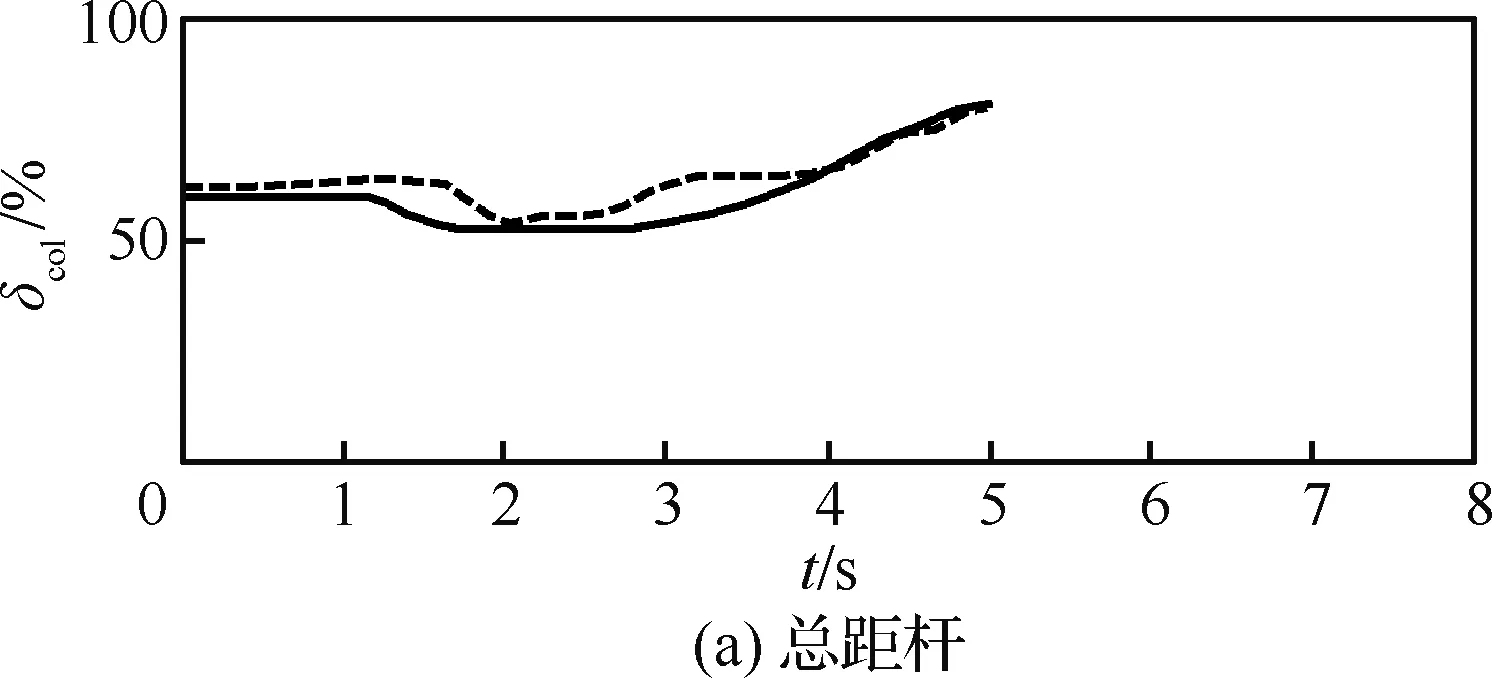
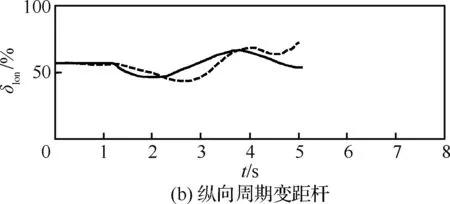
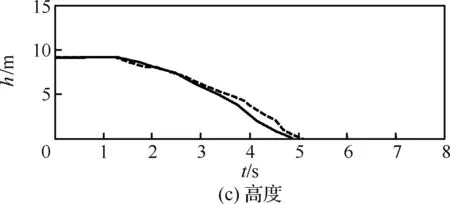
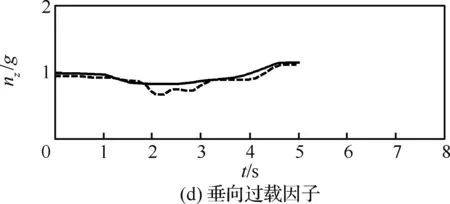
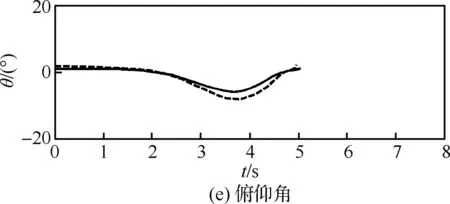
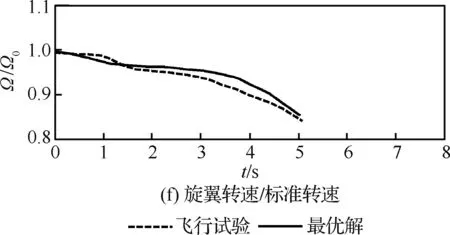
图3 单发失效最优自转着陆计算与飞行试验数据对比Fig.3 Comparison of calculated optimal autorotation landing procedure in one engine inoperative and flight test data

4 计算结果与分析

UH-60A直升机在总重较低(小于7 407 kg)时，单发失效后的回避区很小，甚至消失。为了能较为明显地看出旋翼转速对低速回避区的影响，本文采用总重为9 185 kg的UH-60A直升机进行计算分析。同时假设单发失效时直升机处于标准大气压下的配平状态，并考虑1 s的驾驶员反应延迟时间。其中末端约束、路径约束和性能指标的取值与第3节一致。

4.1 旋翼转速对直升机需用功率的影响

图4显示了低速范围内不同旋翼转速下的直升机需用功率，其中Ω0为直升机标准旋翼转速1 hp=0.735 498 7 kW。单台发动机的最大可用功率也显示在图中。可以看出，随着旋翼转速的降低，需用功率会减小。但当旋翼转速降低到某一特定值时(即80%Ω0，对应前飞速度范围0 ～20 m/s)，随着旋翼转速的降低，需用功率会开始增加。这是因为旋翼转速过低时，反流区增大，桨叶段的失速带来了更大的旋翼功率损失。图4不再讨论比76%Ω0更低的旋翼转速，这是因为此时驾驶员的总距杆操纵量已经接近满行程。除此之外，当旋翼转速继续下降时，直升机的前进比不断增大，旋翼桨盘两边的气流不对称性加剧，直升机难以配平。

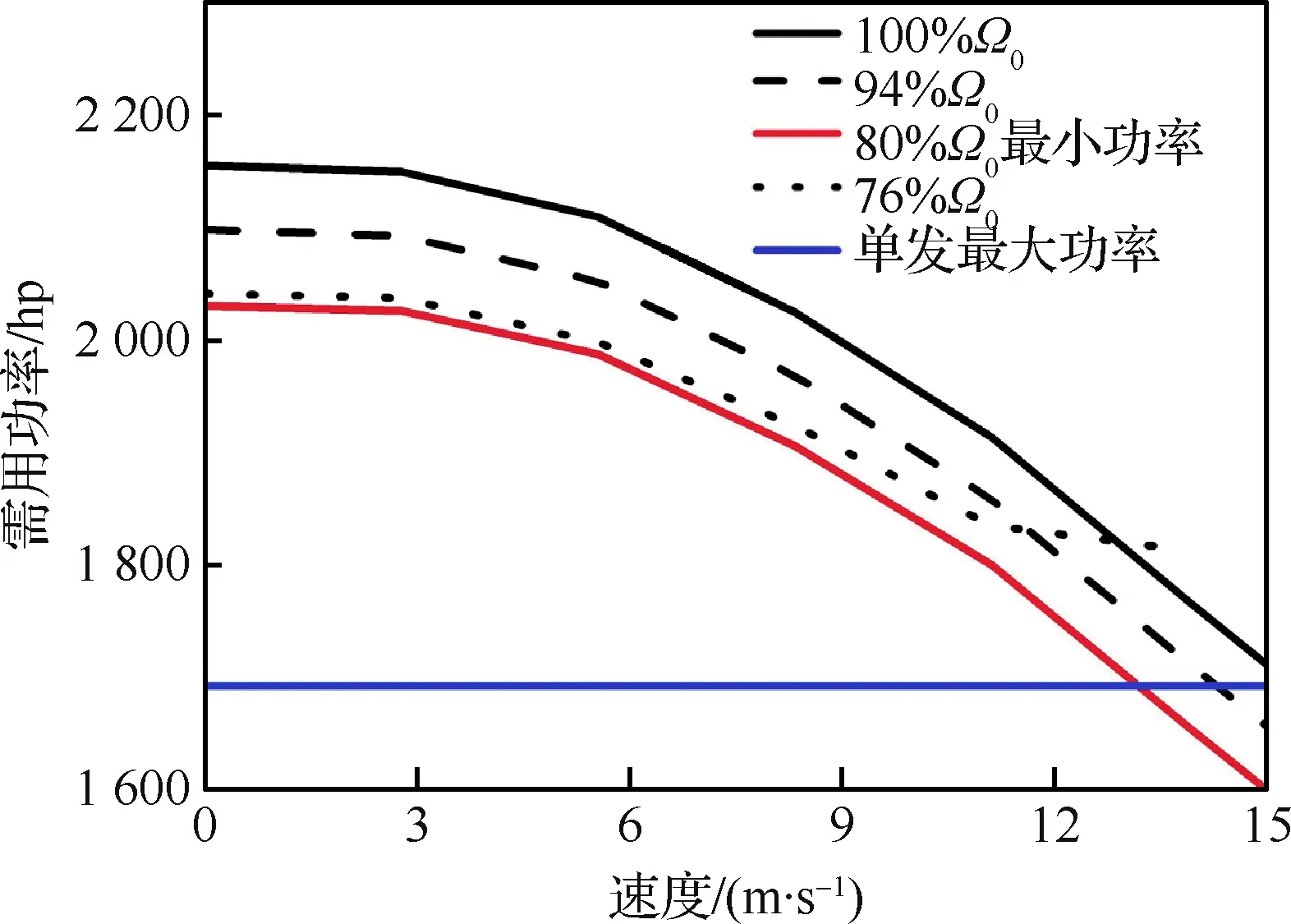
图4 低速区直升机需用功率随旋翼转速的变化Fig.4 Variation of helicopter required power with rotor speed in low-speed zone

4.2 旋翼转速对低速回避区的影响

图5显示了各旋翼转速下发生单发失效后的H-V曲线。可以看出，当旋翼转速从100%Ω0降低到84%Ω0时，回避区的面积逐渐缩小。这是因为直升机的需用功率与剩余发动机最大可用功率之间的差距随着旋翼转速的降低而变小，这有利于直升机单发失效后的自转着陆。而当旋翼转速从84%Ω0降低到76%Ω0时，回避区的面积迅速增大。这主要是因为此时存储在旋翼中的动能过低，且需用功率达到最低后逐渐开始增大，不利于直升机单发失效后的自转着陆。

图6进一步显示了4个旋翼转速(其中包括最小需用功率对应的旋翼转速)下直升机单发失效后的低速H-V曲线。可以发现，达到最小H-V 区域时所对应的旋翼转速(84%Ω0)略高于最小需用功率对应的旋翼转速(80%Ω0)。这是因为虽然在80%Ω0下，直升机的需用功率最低，但是此时存储在旋翼中的动能也较小，因此最优的自转着陆性能需要更高的旋翼转速，即84%Ω0。

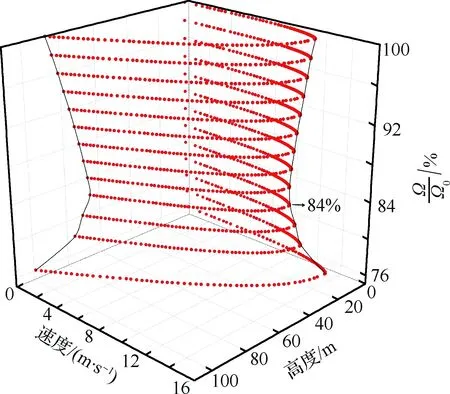
图5 各旋翼转速下单发失效后的H-V曲线Fig.5 H-V curve of different rotor speeds after one engine inoperative

图6 4个旋翼转速下单发失效后的H-V曲线Fig.6 H-V curves of 4 rotor speeds after one engine inoperative

此外，这两个旋翼转速下的回避区非常接近，说明旋翼转速在80%Ω0～84%Ω0之间时，不仅能有效降低直升机的需用功率，还能提高直升机单发失效后的自转着陆性能。

4.3 旋翼转速对单发失效自转着陆的影响

图7～图9显示了不同旋翼转速下，H-V曲线上3个关键点(高悬停点、拐点和低悬停点)的最优单发失效自转着陆过程，从图中可以得到以下结论：

1) 各个旋翼转速下，3个关键点对应的最优自转着陆轨迹、速度和俯仰角变化均较为合理。在高悬停点处(图7)，直升机存在显著的低头俯冲加速和抬头减速的现象(图7(d))。驾驶员先压杆降低总距维持转速(图7(e))，然后着陆时提杆增大总距(图7(f))减小触地速度(图7(b)和图7(c))；在拐点处(图8)，注意到76%Ω0时只有抬头减速的现象(图8(d))，这是因为在该旋翼转速下拐点对应的前飞速度较大(14.2 m/s)，驾驶员需要首先减速才能保证触地时的前飞速度在规定范围以内(12.2 m/s)。此外，旋翼转速与驾驶员总距杆的变化与图7基本一致，但幅度较小；在低悬停点处(图9)，直升机几乎垂直降落(图9(a))，但触地速度不大(图9(b)和图9(c))，驾驶员操纵幅度较小(图9(f))。

2) 随着旋翼转速降低至76%Ω0，3个关键点上的驾驶员初始总距杆量均接近最大行程。尤其是在高和低悬停点处，总距杆量超过了90%，且需要维持最大操纵行程近1 s的时间(图7(f)和图9(f)中的虚线)，期间失去了控制余量，不利于飞行安全。再加上此时旋翼本身储存的动能较小，且需用功率开始增大，导致旋翼转速在76%Ω0时单发失效低速回避区的面积迅速增大(图5和图6)。

3) 在80%Ω0和84%Ω0的旋翼转速下，驾驶员的初始总距杆量会增加，但仍旧留有一定的控制余量，因此直升机在自转着陆时可以充分利用旋翼储存的动能。虽然旋翼储存的动能会降低，但由于旋翼需用功率也大幅降低，因此剩余发动机提供的最大可用功率可以使其更加顺利地完成单发失效后的自转着陆过程。

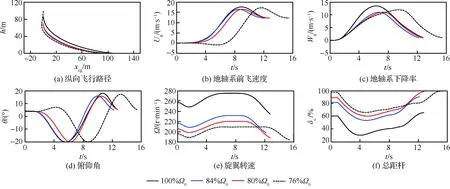
图7 单发失效最优自转着陆过程(4个转速、高悬停点)Fig.7 Optimal autorotation landing procedure with 4 rotor speeds at high hover point after one engine inoperative

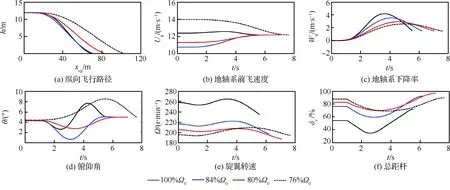
图8 单发失效最优自转着陆过程(4个转速、拐点)Fig.8 Optimal autorotation landing procedure with 4 rotor speeds at knee point after one engine inoperative

图9 单发失效最优自转着陆过程(4个转速、低悬停点)Fig.9 Optimal autorotation landing procedure with 4 rotor speeds at low hover point after one engine inoperative

5 结 论

以UH-60A直升机为例，利用最优控制方法研究了变转速旋翼直升机在遭遇单发失效时，旋翼转速对自转着陆低速回避区和最优自转着陆过程的影响。

1) 降低旋翼转速可明显减小直升机的需用功率，但是过低的旋翼转速反而会带来旋翼需用功率的增加，并会导致总距杆的控制余量不足，以及引发配平问题。

2) 适当降低旋翼转速可以减小直升机的需用功率与剩余发动机最大可用功率之间的差距，但也会减小存储在旋翼中的动能。因此，要达到最优的自转着陆性能，必须综合考虑旋翼转速对以上两个方面的影响。本文算例中，随着旋翼转速的降低，直升机单发失效后的低速回避区首先会逐渐缩小，然后迅速增大。最小回避区对应的旋翼转速略高于最小需用功率对应的旋翼转速。旋翼转速在80%Ω0～84%Ω0之间较为合理。

3) 本文计算的各旋翼转速下的最优自转着陆过程较为合理。在算例中，当旋翼转速降低至76%Ω0时，回避区3个关键点上的驾驶员总距杆变化均接近最大行程，容易失去控制余量，不利于飞行安全。再加上此时旋翼本身储存的动能较小，且需用功率开始增大，使得旋翼转速在76%Ω0时单发失效低速回避区的面积迅速增大。

4) 在80%Ω0和84%Ω0的旋翼转速下，驾驶员的总距杆量仍旧留有一定的控制余量，直升机在自转着陆时可以充分利用旋翼储存的动能。虽然旋翼储存的动能会降低，但由于旋翼需用功率也大幅减小，因此剩余发动机提供的功率可以使其更加顺利地完成单发失效后的自转着陆过程。