曲面积分的计算与应用研究
梁宏伟
(长春市养正高级中学数学组,吉林 长春)
曲面积分是微积分理论的重要内容,具有高度的抽象性和严谨性,同时也具有广泛的应用性。
一、第一型曲面积分的概念与性质
定义设∑为光滑曲面,函数f(x,y,z)是定义在∑上的有界函数。把∑任意分成n个小块△Si(i=1,2,…,n),△Si也表示其面积。在△Si上任取一点(ξi,ηi,ζi),用λ表示∑的直径中最大者。如果极限存在,
则称此极限值为函数f(x,y,z)在曲面∑上的第一型曲面积分,或对面积的曲面积分,记为
第一型曲面积分的性质:
性质1(线性性质)设函数f,g在光滑曲面S上的第一型曲面积分存在,k1,k2是两个常数,则k1f+k2g在S上的对面积的曲面积分也存在,并且
性质2(可加性)设函数f在光滑曲面S上的第一型曲面积分存在,S可划分为两个光滑曲面 S1,S2,则 f在 S1,S2上的第一型曲面积分都存在;反之,如果f在S1,S2上的第一型曲面积分都存在,则f在S上的第一型曲面积分也存在,即
当S为唯一封闭曲面时,习惯上把f(x,y,z)在S上的第一型曲面积分面积记为
二、利用曲面方程化曲面积分为二重积分计算
分析 ∑在xOy面上的投影区域比较宽泛,故将曲面积分转化为xOy面上二重积分比较方便。
∑在xOy面上的投影区域为D:x2+y2≤2x
于是,有
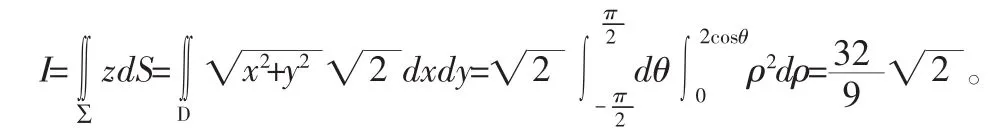
由积分曲面的形状来决定曲面向哪个坐标面(如xOy面)投影,然后将曲面方程改写为该坐标面上的显函数(如z=f(x,y)),最后由此曲面方程表达面积元素(如
分析 因为柱面x2+y2=R2在平面xOy上的投影区域为一条曲线圆x2+y2=R2,其面积为0,所以不能往xOy平面上投影,可向yOz平面(或向zOx平面)投影,但是曲面关于另两个坐标面都是对称的,可以应用对称性定理简化计算。
解 由对称性定理知,∑关于zOx平面和yOz平面对称,被积函数关于y与x为偶函数,设∑1表示∑的位于第一卦限的部分,则有

例3 计算下列曲面积分:
分析 积分曲面∑均为球面x2+y2+z2=a2,关于三个变量具有轮换对称性,被积函数的每一项的对应法则又一致,又由于积分曲面的方程可以代入被积函数中去,从而可以应用轮换对称性简化计算。
计算曲面积分时,应注意观察其积分的特点,选取恰当的方法可以简化计算。
若满足对称性定理转化为第一卦限的部分来计算,各积分的上、下限均为非负数,使得计算方便。
通过对曲面积分的研究,我们更加深刻地理解了曲面积分的重要性,尤其对曲面积分计算方法与应用的研究,例如我们可以通过第一型曲面积分求曲面的面积、质量、转动惯量等;通过第二型曲面积分求通量、散度、旋度、流量等。

