透过现象本质,探究教材细节
——“6.2正切函数的图象与性质”案例分析
丁泽楠
(上海师范大学附属中学,上海)
一、教材解读
教材由细节构成,每一个细节都是教材发展的一个生长点,我们认为这些生长点是解读教材好的出发点。寻求合理化、智慧化和精确化的教学当然可以推出精彩的课堂教学。
1.注意教材的插图细节,分析教材内容
细节是什么?教材的每一个插图都有其内涵。一般来说,图形直观形象,其通常是在教学中教材的文字语言往往不能正确形容某种意义或过程的时候所使用。
2.探究教材本质,挖掘教材细节
数学探究能力在日常的教学过程中为学生学习提供了基础保障,利用一切可能的机会和素材,使学生的探究能力得到发展。本文以沪教版高中数学教材中“正切函数的图象与性质”为例,通过类比数学内容之间的关系来培养学生探究能力。本文的教学内容是由教师的问题和指导来决定的,通过学生对现有学习探究的体会,学生会探究正切函数的图象和性质,并利用探究过程形成学习函数的一般方法。
二、教学过程
1.激发学生原有的认知水平,从结构和整体入手
【教学过程片段之一】
师:我们有同学类比正弦函数的定义,定义一个正切函数:对于任意一个实数x都有唯一确定的值tanx与它对应。按照这个对应法则建立的函数关系,表示为y=tanx,叫做正切函数。请问大家,这个定义合理吗?
师:今天,我们就来研究正切函数的图象与性质,那么,作函数图象的常用方法是什么?
生:描点法。
师:描点法是我们作函数图象的最基本方法,还有其他方法吗?
生:单位圆,借助正切线,类比正弦函数的方法。
师:大家想,我们在画y=cosx图象时利用了平移,目前平移也是我们作图象的方法之一。那么,正切函数的图象,你会选择哪一个方法画?(描点法)因为它没有办法通过我们熟悉的函数平移来得到。

师展示学生画的正切函数图象。
师:老师借助单位圆画出y=tanx的图象,让学生观看。
【思考】主要是让学生体会研究函数的一般思想方法(数形结合),让学生自主画图,寻找思维冲突源,为本节课优先研究性质做思想基础。先探究正切函数的性质,再作图验证,这与前面研究正弦函数、余弦函数恰好相反。教师要深刻挖掘教材这样编写的意图,加强学生的理性思考,使数形结合的思想体现得更加全面。
【教学过程片段之二】
师:我们从正切函数y=tanx的图象上看它是否也具有正弦函数y=sinx的一些性质呢?我们一起来探究总结归纳正切函数的图象及性质。首先,我们来看定义域、值域、周期。
师:理由呢?
师:说得对,根据你所说的T=π,也可证明π是y=tanx的最小正周期。
生:假设 0<T0<π 是正切函数的周期,则 tan(x+T0)=tanx恒成立,取x=0

∴0<k<1与 k∈Z 矛盾,T=π 是 y=tanx的最小正周期。
师小结:要证明π是最小正周期,需要证明任何一个比0大、比π小的数不可能是它的周期,从正的方面去证,这不可能的,有无数多个数,所以我们想到反证法。
【思考】正切函数的定义域如何反映图象的特征,对学生而言是一个难点。我通过引导学生类比正弦函数的图象特征,利用已有的活动经验来加以理解。在课堂教学中,教师需要挖掘教材的细节,尝试挖掘教材细节中的丰富内涵,这是学生获取知识的主要来源,教师应有效探索和开拓发掘,有效生成,并将其作为课堂上的亮点。
【教学过程片段之三】
师:那么正切函数的奇偶性、单调性如何?
师:说得对,根据你说的也可证明,即
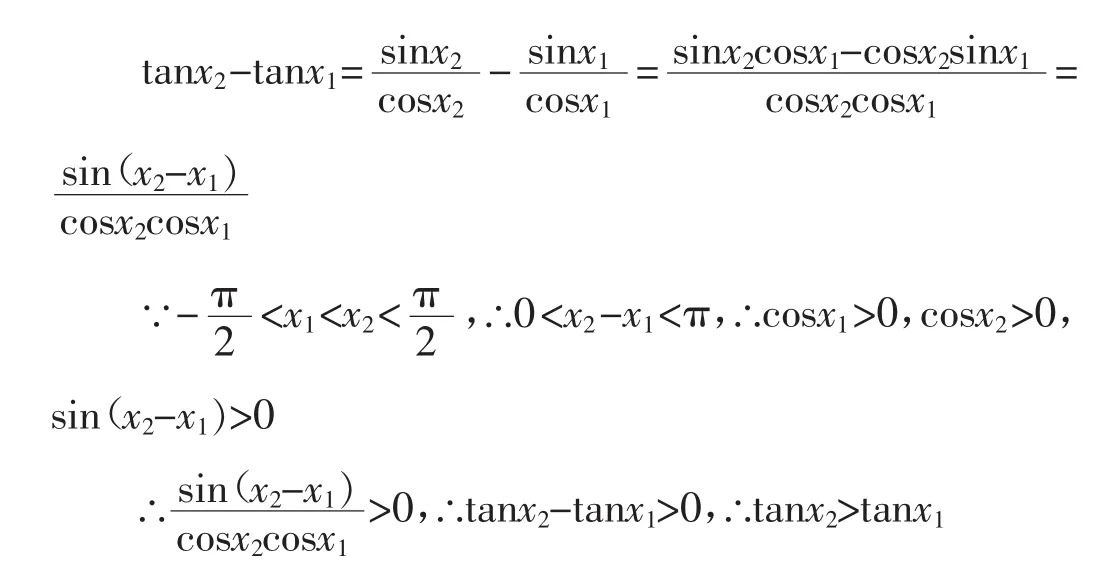
师:那么对称中心呢?
生 2:(kπ,0),k∈Z
师:对称轴、渐近线方程呢?
【思考】从正切函数的性质可以比较容易地得到周期性和奇偶性,这样能够激发学生的学习热情。研究正切函数的对称性与单调性是学习的一个难点,学生容易形成“思维定式”。通过问题引领学生类比正弦函数及余弦函数,建构概念。教师在课堂上需要给学生思考留点时间,再引导其用三角函数线解决问题,从特殊的一个周期到一般的区间,让知识在学生不断的思考中自然生成并且在思维的基础上有较大突破和理解。研究图象的性质是高中学生必须具备的一种能力,学生应深度把握教材细节。
【教学过程片段之四】
师:总结归纳正切函数的图象及性质内是增函数,

正切函数 y=tanx定义域 {x|x≠kπ+π值 域 R(无最大值,无最小值)2 ,k∈Z}周 期 T=π奇偶性 奇函数2 ,kπ+π2),k∈Z对称中心 (kπ单调性 增函数,增区间为(kπ-π 2 ,0),k∈Z 对称轴 无渐近线方程 x=kπ+π 2 ,k∈Z
师:我们在画正弦函数和余弦函数的图象时,用描五个点的简单方法,那么在画正切函数的图象时,我们也有简单的方法,可以画出大致图象,怎么画呢?
【思考】引导学生归纳出研究函数的一般方法,为以后研究新的函数积累经验与方法。
回顾探究过程,扫描知识漏洞,形成知识体系,深刻体会研究数学问题的一般方法和思路,培养学生的综合概括能力和语言文字的表达能力。
2.在探索中将隐含学生理解的滞后,还原课堂学习反馈效果,体验知识的应用
【教学过程片段之五】
在同学们已经掌握了正切函数y=tanx的定义域、值域、周期性、奇偶性、单调性、对称中心和图象的性质后,现在可以做一些练习:
课堂练习1:(1)根据正切函数的图象,分别写出满足下列条件的集合:
①tanx=-1_______________________;
②tanx>0________________________
例2:求证:函数f(x)=Atan(wx+φ)的最小正周期
【思考】通过课堂练习和例题的讲解,进一步巩固知识,强化对学生基本技能的训练和解题的规范化训练,提高学生课堂及时应用新知和解决问题的能力,体现了因材施教的方法,也挖掘了细节的内涵,研究了教材的本质。
三、教学思考
本课探索了正切函数的图象与性质,将知识、方法和能力融合为“三位一体”的性质研究教学,突显探究教学的开放性。教师引导学生从函数性质形成过程、性质的探究过程中,用研究正弦函数的图象性质类比,再利用数形结合思想,通常由数(性质)—形(图象)—数(性质)来探索正切函数的图象及其性质。师生共同构建函数图象性质的研究过程,体验了数学的重要思想和方法。在探究过程中,教师要把握性质的生成机会,如何把握?把握的程度如何?笔者结合自己多年的教学实践,形成了如下认识:
1.研究教材细节,透过现象看本质。创设认知情境,并对已给的教材进行适当整合,并且类比正弦函数与余弦函数的图象与性质的研究。在研究正切函数图象与性质类比中发现,正切函数的研究顺序却恰恰相反,教材是从一个新的角度来研究正切函数的性质,因此在课堂上设计了让学生先小组分别画图的环节,使学生在教学的疑惑中,思考要解决问题的方法,这样本节课的研究思路就自然展开。
2.教学中将探索性质的探究方法作为铺垫。教师引导学生作图,立即引起师生共鸣。通过这种方式,研究代数方法的性质,正切函数的图象与正弦曲线类似,然后通过观察图象来验证性质,并且获得了函数的对称性,加深学生对代数形式的理解,并紧密联系课堂研究的主线、引导的数量和形式的数量。
3.教师也应该为学生探究和挖掘教材的细节,吃透教材,得到函数图象与性质研究结果,提供结果反思和验证的空间,要让学生对数学知识的生成提供反思和研究经验,并进行适当的总结以及深刻的比较。在教学过程中,教师不能急于求得数学性质结果,而应尽可能让学生有更充足的时间对数学概念形成“自然生长”。只有尊重教材,将教材的作用充分展现,并发挥到极致,才能体现教材的价值。
4.在准备这样一堂课的过程中,笔者也花了很多时间,并且思考了很多问题,如:如何让教师“教”得更多,同时让每一位学生“学”得更多?教师问题引领、渗透教材与学生自主探究教材的“度”如何处理?如何处理“部分”和“整体”的关系与区别?学生只有会思考,掌握解题的技巧与方法,才能从题海中走出来,希望能得到各位同行的不吝指导。

