基于动态学习的泊位调度方案优化
王 军,郭力铭,杜 剑,王美蓉
(大连海事大学交通运输工程学院,辽宁大连116026)
0 引言
为充分利用码头资源,保证船舶能够顺利靠泊,码头通常需要依据计划期内预计到港船舶的船型尺寸、到港时间、装卸货量,制定包括船舶靠泊位置、靠泊时间、分配岸桥数量的泊位调度方案.泊位调度方案的合理与否,对码头与船方均会产生影响.对码头而言,由于泊位与岸桥资源是有限的,泊位调度方案的不合理会造成严重的资源浪费;对船方而言,泊位调度方案不合理会导致船舶装卸时间的延长,甚至严重扰乱后续船期计划.对此,本文将对泊位调度方案优化问题展开研究.
在优化泊位调度方案时,码头需要根据在泊船舶的占用泊位情况及预计在泊时间,确定其他待泊船舶的靠泊位置与靠泊时间.在计算预计在泊时间时,曾庆成等[1]用船舶装卸箱量与岸桥装卸效率相除;Zhen等[2]考虑了航道中船舶流量的影响;常祎妹等[3]认识到岸桥作业时存在相互干扰;Golias[4]和Han[5]假设在泊时间分布的概率密度已知.为减少在泊时间的计算偏差,Xu等[6]为靠泊船舶设置了缓冲时间,并提出了处理随机干扰的响应恢复策略;Karafa等[7]从历史数据中挖掘船舶延误概率,再基于此概率函数进行在泊时间计算;Zhen[8]当在泊时间分布已知时构建了泊位分配的随机优化模型,未知时则构建了鲁棒优化模型.然而,上述文献中的在泊时间分布都是固定不变的,而实际中各种因素对在泊时间的影响程度却是动态变化的.如风力通过影响岸桥吊具的摇摆幅度,海浪通过影响船舶的摇摆幅度,导致岸桥装卸效率的降低.而不同季节的平均风级与平级浪高存在明显差异,所以对装卸效率的影响程度并不相同.
本文设计了在泊时间计算函数的动态学习方法,再基于所学习函数进行泊位调度方案优化.即利用泊位调度方案的实际执行结果,借助神经网络方法对在泊时间计算函数进行逐天修正,以实现计算函数随环境的动态更新.另外,本文设计了包含在泊时间动态学习及泊位调度方案优化的并行算法,前者为后者提供更新的在泊时间计算函数,后者的实际执行结果为前者提供学习样本.
1 问题描述
泊位调度方案优化问题是个二维背包问题,泊位调度方案可以用二维图表示,如图1所示.图1的横轴为时间轴,纵轴为岸线轴;用矩形框表示到港船舶,矩形内阴影正方形的个数为分配岸桥数量;矩形左下角的横纵坐标分别为船舶的靠泊时间、靠泊位置,矩形的长宽分别为船舶在泊时间、所占岸线长度.
在制定泊位调度方案时,同一时刻同一位置只能安排一艘船舶,同一时刻所有船舶所占岸线长度之和不能超过码头的岸线总长度.任意船舶的分配岸桥数量不能超过该船舶允许的岸桥数量区间,且所有船舶的分配岸桥数量不超过码头的岸桥总数量.为吸引船舶挂靠,当码头的计划离泊时间超过船舶的要求离泊时间,码头需向船舶支付延误赔偿.对此,虽然通过增加岸桥数量可以缩短在泊时间,但岸桥使用成本是随之增加的.为了降低泊位调度方案的总成本,需要对上述两种成本进行权衡.
本文采用神经网络方法来拟合在泊时间计算函数,将船舶的靠泊时间、装卸箱量、分配岸桥数量、岸桥装卸效率、泊位水深、平均风级及平均浪级作为输入参数,实际在泊时间作为目标参数.通过不断减小在泊时间的计算结果与目标参数间偏差,帮助拟合高质量的在泊时间计算函数.进一步地,借助泊位调度方案及其实际执行结果对计算函数进行逐天修正,可以实现计算函数随环境的动态更新.

图1 泊位调度方案二维图Fig.1 Two-dimensional chart of berth scheduling scheme
2 基于动态学习的泊位调度方案优化模型
2.1 研究假设
(1)以集装箱码头的连续型泊位为研究对象.
(2)码头的岸线长度已知,前沿水深能满足所有船舶的吃水要求.
(3)码头的岸桥总数量已知,每台岸桥的装卸效率已知,不考虑岸桥的移动时间.
(4)船舶到港计划已知,每艘到港船舶都必须被服务,且只服务1次.
(5)船舶到港后才被安排靠泊,每艘船舶靠泊后就不能移泊.
(6)任意两艘靠泊船舶间要留有固定的安全距离.
(7)船舶装卸箱量均以标准箱计数,不考虑因配积载问题产生的倒箱时间.
2.2 模型参数
S={1,…,i,…,I}——计划期内的到港船舶集合,I为到港船舶总数量,i为第i艘到港船舶;
Q={1,…,j,…,J}——码头的岸桥集合,J为岸桥总数量,j为第j台岸桥;
T={1,…,t,…,N}——计划期的时间段集合,N为时间段总数量,t为第t时间段;
li——船舶i的长度;
Wi——船舶i的装卸箱量;
Ai——船舶i的预计到港时间;
di——船舶i的要求离泊时间;
q1i——船舶i允许的最小岸桥数量;
q2i——船舶i允许的最大岸桥数量;
L——码头的岸线总长度;
r——船舶间安全距离;
η——每台岸桥的装卸效率;
c2——每台岸桥的单位时间使用成本;
c1i——船舶i未满足要求离泊时间时,码头向船舶支付的单位时间赔偿成本;
P——泊位调度方案的总成本;
f1i——神经网络训练前船舶i的计算在泊时间;
F()——神经网络训练后的在泊时间计算函数,括号内是输入参数;
f2i——神经网络训练后船舶i的计算在泊时间;
Di——神经网络训练后船舶i的计算离泊时间;
Qit——第t时间段内船舶i的分配岸桥数量;
λi——船舶i靠泊位置的水深;
O1——计划期内平均风级;
O2——计划期内平均浪级;
M——一个足够大的数.
决策变量:
Bi——船舶i的靠泊位置;
Hi——船舶i的靠泊时间;
Zitq——0-1变量,若第t时间段内船舶i被岸桥q服务则为1,否则为0;
Xij——0-1变量,若船舶i早于船舶j停靠则为1,否则为0;
Yij——0-1变量,若船舶i停靠在船舶j左侧则为1,否则为0.
2.3 模型构建

式(1)为目标函数,模型以最小化码头的延迟离港赔偿与岸桥使用成本之和为目标.式(2)表示任意时间段内船舶分配岸桥数量之和不超过码头的岸桥总数量;式(3)用于计算第t时间段内船舶i的分配岸桥数量;式(4)要求船舶到港后才能被安排靠泊;式(5)根据船舶装卸箱量及岸桥装卸效率,计算训练前的船舶在泊时间;式(6)采用动态学习后的计算函数,重新计算船舶在泊时间;式(7)用于计算船舶离泊时间;式(8)保证任意船舶的装卸箱量都能得到满足;式(9)约束任意船舶的离泊时间在计划期内;式(10)~式(14)用于约束岸线同一位置同一时间段内只靠泊1艘船舶;式(15)保证任意船舶i的靠泊位置在岸线长度范围内;式(16)和式(17)保证船舶i的分配岸桥数量在其允许的岸桥数量区间内;式(18)定义了0-1变量;式(19)定义了变量所属集合.
3 算法设计
3.1 算法流程
本文设计了包含动态学习过程的智能启发式算法.算法分为2个独立运算部分:第1部分运用粒子群算法进行泊位调度方案优化,第2部分运用神经网络算法进行在泊时间计算函数的动态学习.其中,第1部分是算法主体.计划期开始前,将第2部分拟合完毕的在泊时间计算函数提取至第1部分,进行泊位调度方案优化模型的求解;计划期结束后,将泊位调度方案的实际执行结果反馈至第2部分,作为学习样本继续对已有在泊时间计算函数进行动态修正.基于此并行运算流程,泊位调度方案优化模型的求解时间不会增加,但在泊时间的计算准确性与调度方案的优化效果却在持续提升.具体的算法流程如图2所示,图2的左侧为第1部分,右侧为第2部分.
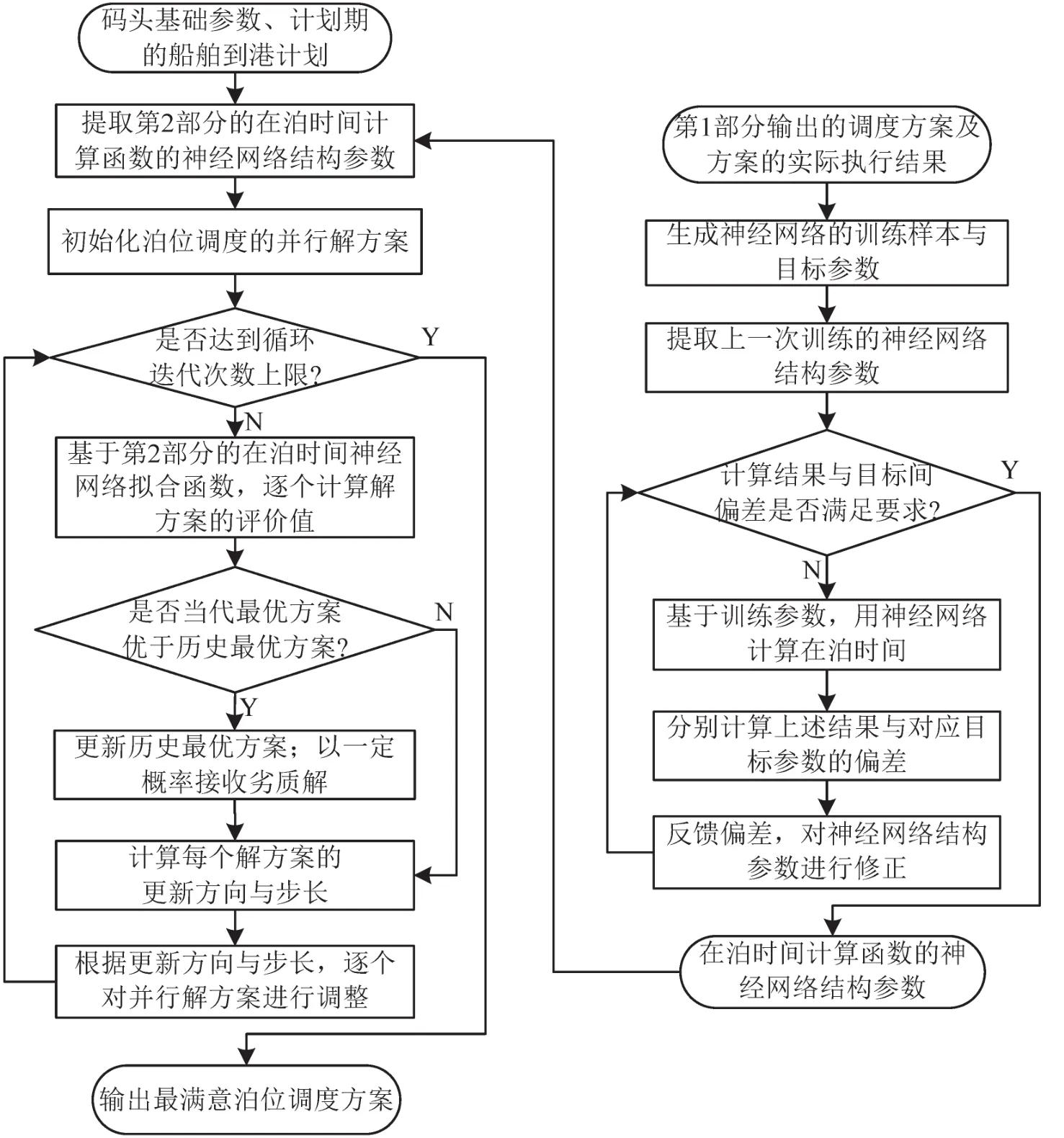
图2 算法流程图Fig.2 Algorithm flow chart
3.2 关键步骤
(1)泊位调度方案优化的粒子群算法.
粒子群算法中,解方案采用表1的编码方式.以船舶1为例做解释:1号船舶在第10个时间段,停靠在岸线200单位长度处,被分配2台岸桥.

表1 编码方式示例Table 1 Example of encoding method
算法步骤如下:
Step1 从动态学习部分中提取更新的在泊时间计算函数,输入船舶到港计划及码头相关信息.
Step2 设置并行解个数,并对初代解进行随机初始化.
Step3 计算每个解方案的评价值,如果解方案不满足模型约束,将评价值赋值为无限大.
Step4 更新解方案的当代最优位置与历史最优位置.
Step5 计算解的改善方向与步长,并更新并行解中每个解方案的当前位置.
Step6 判断是否满足算法的迭代终止条件,满足则输出最满意解方案,否则返回Step3.
(2)船舶在泊时间的神经网络训练.
神经网络有8个输入参数,需要在输入层设置8个节点.目标参数为实际在泊时间,输出层只设置1个节点.为了提升神经网络拟合能力,增加了隐含层.神经网络训练步骤如下:
Step1 输入1组学习样本,从数据库中提取输入层、隐含层、输出层的节点数、权值wij与阈值θ.
Step2 根据公式计算各神经元的输出.
Step3 计算输出层的计算结果与目标参数间偏差,判断偏差是否符合要求,是则执行Step5.
Step4 使用梯度下降法对权值与阈值进行更新,再返回Step2.
Step5 将训练完毕的神经网络结构参数存入数据库.
4 算例分析
4.1 在泊时间动态学习有效性的分析
通过动态学习过程中在泊时间计算偏差的变化情况,验证动态学习可以提升在泊时间的计算准确性.将2017年某码头的泊位调度方案与实际执行结果按周分为52组,每组包括100个样本.随机抽取连续的6组样本,第6组作为测试样本,第1-3组、2-4组与3-5组依次作为学习样本.假设训练前在泊时间服从正态分布.基于训练前计算函数,对第1-3组样本进行第1次动态学习;再基于第1次更新的计算函数,对第2-4组样本进行第2次动态学习.依此类推,始终基于最新函数进行动态学习,以实现计算函数随环境的动态更新.
基于训练前计算函数,以及动态学习后的3个计算函数,计算100个样本的输出结果与目标参数间平均偏差,作为1次实验.连续进行10次实验,并绘制各次实验中4组平均偏差的柱形图,平均偏差越小则计算越准确.由图3可知:各次实验中,动态学习后的平均偏差有所下降,越后期更新的计算函数的平均偏差越小.可见,动态学习过程是有效的.
4.2 泊位调度方案优化效果的对比分析
码头岸线长度800 m,岸桥总数量6台,岸桥作业效率35 TEU/h;岸桥使用成本300 USD/h,船舶延误赔偿20 000 USD/h;计划期开始时间为2018年1月1日0点,共48 h;计划期内的船舶到港计划如表2所示.

表2 船舶到港计划Table 2 Vessels arrival plan

图3 动态学习中在泊时间计算的平均偏差Fig.3 The mean deviation of handling time calculation in dynamic learning
对上述52组样本进行动态学习,得到最新的在泊时间计算函数.基于最新计算函数制作推荐方案,简称为方案1;基于训练前计算函数制作对比方案,简称为方案2.将方案1绘制于图4,方案2绘制于图5.图中的矩形框表示到港船舶,矩形左下角的横纵坐标分别为船舶靠泊时间、靠泊位置,矩形内阴影正方形的个数为分配岸桥数量.将方案1与方案2的结果差值列于表3,可知:方案1和2存在较大差异,两方案中7条船舶的平均在泊时间相差2.0 h,总成本相差71 511美元.由于训练前在港时间计算函数的准确性有限,导致计算离泊时间、分配岸桥数量及方案总成本均不准确.可见,动态学习过程是必要的.
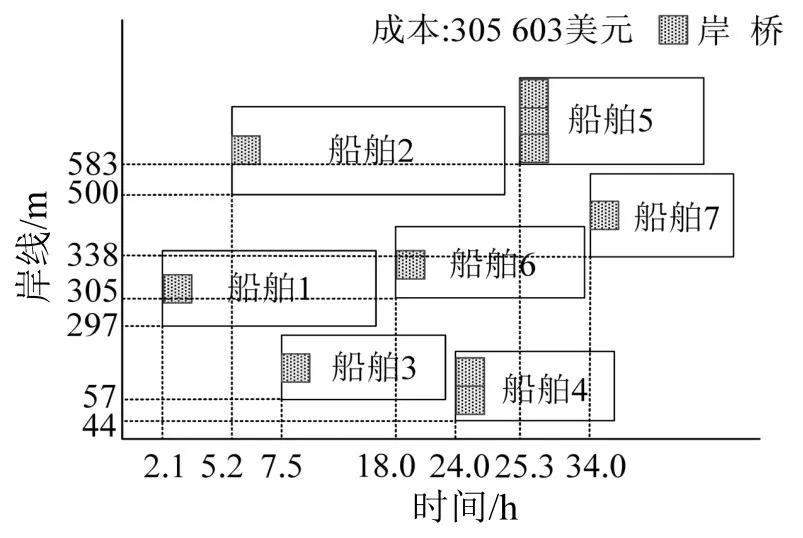
图4 泊位调度方案1Fig.4 Berth scheduling scheme 1

图5 泊位调度方案2Fig.5 Berth scheduling scheme 2

表3 方案1与方案2的结果差值Table 3 Difference in results between scheme 1 and scheme 2
由于方案2的计算准确性有限,与方案1的结果差值不能真实地反映优化效果.对此,基于最新的在泊时间计算函数,在不改变方案2的靠泊时间、靠泊位置及岸桥数量的前提下,对各船的在泊时间、离泊时间及方案总成本进行重新评估,得到方案3.将方案2与方案3的结果差值列于表4,由表4可知:方案3中各船的在泊时间、离泊时间及方案总成本均在增加,说明训练前函数的计算结果偏小,这主要是因为其未考虑冬季风高浪大对装卸效率的影响;在泊时间的增加导致多条船舶不能按时离泊,造成了延误赔偿的急剧增加.进一步地对比方案优化效果,将方案1与方案3的结果差值列于表5,由表5可知:方案1比方案3的平均在泊时间缩短2.4 h,成本降低11.1%,且两方案的求解时间仍均小于1 min.可见,在求解时间不会增加的前提下,动态学习可以提升泊位调度方案优化效果.

表4 方案2与方案3的结果差值Table 4 Difference in results between scheme 2 and scheme 3

表5 方案1与方案3的结果差值Table 5 Difference in results between scheme 1 and scheme 3
5 结论
本文构建了基于在泊时间动态学习的泊位调度方案优化模型,在提升在泊时间计算准确性的基础上,降低了方案总成本.设计了包含动态学习过程的智能启发式算法,在保证泊位调度方案优化模型的求解时间不会增加的前提下,可以提升泊位调度方案的优化效果.但考虑到动态学习过程可能遭遇样本数量少及质量差的情况,后续研究会尝试借助强化学习方法,对动态学习过程的学习能力进行增强.

