基于动态定价的共享汽车自适应调度策略

王 宁，舒雅静，唐林浩，张文剑

(同济大学汽车学院，上海201804)

0 引 言

随着中国经济的快速发展和人们生活水平的提高，中国汽车保有量不断攀高，给环境污染、道路安全、城市管理等方面带来了巨大压力.汽车共享在解决居民个性化出行需求的同时，也能缓解汽车产业发展带来的负面影响.

狭义地来说，汽车共享即指汽车分时租赁，汽车分时租赁模式可分为往返式和单程式两种：往返式汽车分时租赁要求用户在同一站点取还车，单程式汽车分时租赁的用户可在任意站点取还车.单程式相对于往返式更加灵活便捷，可满足用户多样化的出行需求，比如购物、娱乐、通勤及某些偶然的出行需求[1].近年来，国内出现的许多汽车分时租赁项目也多为单程式.但是，单程式取还车的灵活性给汽车分时租赁运营商在租赁网络管理维护上带来了困难，各站点很难做到车辆供给与需求的平衡.可能出现有的站点车辆堆积，用户无法还车，而有的站点无车可租，造成订单流失、用户体验较差.因此必须制定有效的车辆调度方案，缓解汽车分时租赁系统的供需不平衡.

通过对国内外相关文献的研究，缓解汽车分时租赁系统供需不平衡的解决办法主要包括以下4种方案：第一是人工调度，员工将车辆从富裕站点调至稀缺站点；第二是订单择优，根据该订单对系统平衡的影响决定是否接受该订单；第三是优化布局，在运营之初做好站点选址及车辆配置工作；第四是自适应调度，以价格为杠杆调节各个站点的需求量[2].其中，前3种方案受到国内外诸多科研学者关注，但自适应调度策略领域研究较少.但就实施效果比较而言，由于消费者需求变动，事先优化站点布局与车辆配置的方案无法有效缓解实际运营中的供需不平衡；订单拒绝策略降低了订单接受率，对用户体验造成损害；车辆调度方案具有较长的滞后期，且人工调度成本较高；自适应调度策略则可以利用价格激励改变用户行为，实时缓解系统供需不平衡.

Balac等[3]利用Agent-based模型研究停车价格对于自由式汽车共享需求的影响，发现增加停车价格有利于提高使用率.Zhou[4]依据需求流动性针对租赁车辆管理提出动态激励机制，并用维也纳出租车数据验证了该方法能有效将车队维持于均衡状态.Min Xu等[5]基于价格对用车需求的影响，利用混合整数非线性非凸规划模型，以利润最大化为目标同时解决了共享电动汽车站点布局、定价策略与调度问题.Jorge等[6]运用一个混合整数非线性规划模型，确定定价策略以实现利润最大化，并将其定义为单程式车辆系统旅程定价问题.王喆[7]基于动态价格激励机制，在传统汽车租赁顾客需求服从非齐次泊松过程的需求下，构建了具有滚动周期的优化特征动态随机模型.上述文献中，有些文章侧重于价格对于站点借车需求的影响，有些文章侧重于对站点还车需求的影响，本文将借车与还车需求相结合，构建一套全新的基于动态定价的自适应调度策略.

1 消费者价格敏感性调研

汽车分时租赁自适应调度策略的核心在于利用价格杠杆调节用户站点借车需求及站点还车需求，因此了解消费者对于分时租赁服务价格的敏感性至关重要.在站点借车时，通过价格调整影响消费者预约订车行为，一般而言，当价格上升时，需求会下降，反之亦然.在站点还车时，可以通过价格优惠引导消费者将车还至车辆稀缺的附近站点.

问卷设计以探索汽车分时租赁借车需求价格弹性和研究价格激励改变还车站点方案接受度的影响机制，本次问卷收集采用网上收集与实地发放两种方式，共收集问卷450份，其中有效问卷402份，有效率达到89.3%.

(1)借车需求价格弹性.

根据图1所示，汽车分时租赁需求与价格关系基本呈现线性负相关，因此本文将采用弧弹性算法求得汽车分时租赁需求价格弹性系数，计算时代入(0.8，0.05)和(0.4，0.41)两点数据.

图1 借车需求—价格关系图Fig.1 The relationship between pick-up demand and price

(2)价格激励改变还车站点方案接受度分析.

本文将利用二元Logistic回归分析消费者对于利用价格激励改变还车站点方案的接受度.在实际调度方案中，常常忽略消费者人口统计变量及其出行习惯，仅考虑减免金额和目的地与还车网点的距离[5]，从而得到

式中：P1——接受激励方案；

P2——拒绝激励方案；

x21——费用折扣；

x19——目的地与换车网点距离.

经检验，模型的卡方值是205.564，显著性为0.000，可见模型十分显著.同时Person卡方统计量和偏差卡方统计量对应的P值大于5%，不能拒绝实际值与预测值一致的假设，说明模型具有较好的拟合优度.

2 自适应调度策略模型

2.1 模型相关变量定义

本文首先选取变量“站点某一时间段平均车位利用率”来量化汽车分时租赁系统内各站点的库存水平以反映供求关系，并将其作为状态变量对站点用车价格进行调节，而价格变化导致借车需求与还车需求发生变动从而影响各站点供求关系，此即汽车分时租赁系统动态定价机制核心.

定义变量如下：

M——汽车分时租赁系统内车辆规模，M为定值；

N——汽车租赁系统内站点集合，N={1,…,n,…,N}，N为定值；

T——将1个时间周期分成T个时间段，t表示第t个时间段，T={1,…,t,…,T}；

Zn——站点n的规模，∀n∈N，站点的规模取决于停车位的数量；

Sn(t)——第t时段结束时n站点可用车辆数，∀n∈N，∀t∈T；

P0——当前租赁服务价格(元/min)；

Pmin——租赁服务价格最小值(元/min)；

Pmax——租赁服务价格最大值(元/min)；

——当天租赁服务价格平均值(元/min)；

Pn(t)——t时段站点借车时服务价格(元/min)；

Bn(t)——t时段前往站点n租赁汽车的顾客数量，即实际借车数量；

(t)——原初价格情况下，t时段预定站点n租赁汽车的顾客数量，即原初借车需求；

Tn(t)——动态价格情况下，t时段预定站点n租赁汽车的顾客数量，即实际借车需求；

(t)——原初价格情况下，t时段前往站点n送还汽车的顾客数量，即原初还车需求；

Rn(t)——动态价格情况下，t时段前往站点n送还汽车的顾客数量，即实际还车需求；

E——消费者借车需求弹性系数；

ωn(t)——站点n在第t个时间段内停车位平均利用率；

ω0——停车位标准利用率；

c1——显示借车服务价格对库存水平变化的敏感性；

c2——显示还车服务价格对库存水平变化的敏感性；

MBE——系统整体不平衡指数.

2.2 模型框架及原理

本节提出了一个闭环负反馈的自控制模型，如图2所示，模型要求如下：给定一个单程式汽车分时租赁系统的站点集合、车辆集合、停车位集合，系统目前OD需求矩阵(借车站点—还车站点)已知，自控制模型旨在以动态定价机制缓解系统的供需不平衡.在此过程中系统不拒绝任何订单，除非站点无车可取.

在任意时段t的结束时刻，站点n的车辆数量与初始时刻车辆数量、该时段内借车数量和还车数量相关，即

图2 汽车分时租赁自适应调度模型原理图Fig.2 The structure diagram of the adaptive scheduling strategy in car-sharing system

实际借车数量需要判断站点车辆规模能否满足消费者的借车需求，以两者的最小值作为实际借车数量，即

在此模型中，借车需求根据需求价格弹性系数随价格的变化而变化，即

在实际情况中，价格弹性系数会随着时间及价格变化幅度的变化而变化，并非一个常量.在本文中采用弧弹性系数，假设需求弹性系数在不同的时间段及价格区间内不变.原因如下：其一，价格变化幅度对价格弹性系数的影响在实际情况中较小，企业一般会将价格设定在参考价格P0上下符合实际的价格区间之内，因此价格波动幅度较小；其二，为了简化计算考虑，本文将价格弹性系数设为常数.

在此模型中，实际还车需求在原初还车需求的基础上，还需考虑由价格变动带来的还车站点的改变，即

r(Rn(t),(t))等于将租赁车辆由原拟定还车站点n*改变为站点n的顾客数量减去将租赁车辆由原拟定还车站点n改变为站点n*的数量，即

影响消费者改变还车站点的关键因素在问卷调研时已得出可靠的研究结论.在本文模型中，假设消费者社会特征不存在异质性，即只考虑减免金额、原拟定还车站点与实际还车站点距离，即

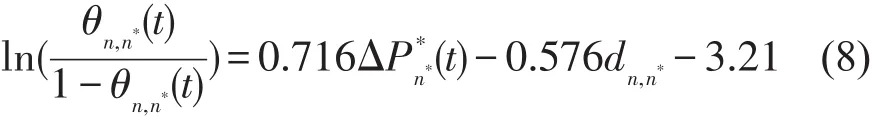
式中：ΔPn*(t)——以打折情况描述n站点t时段的优惠力度，即

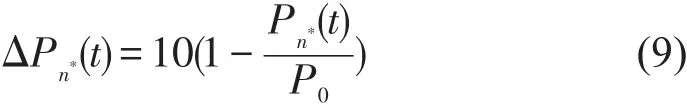
由此可得，消费者愿意将原拟定还车站点n改变为实际站点n*的可能性为

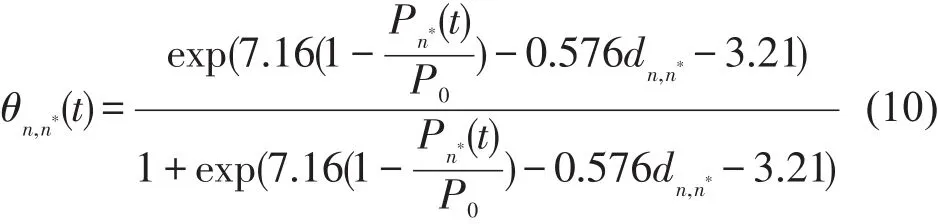
在实际情况中，消费者不可能对考虑系统内所有站点提供的价格减免激励，只可能考虑几个离自己较近的推荐站点，为了限制领域站点的数量，顾客选择接受汽车分时租赁系统各站点价格激励的概率之和不大于1，即

此外，还需考虑到一个约束条件，即该动态定价模型假设条件已经明确车队规模保持不变，因此

上述环节已经构建了动态定价的主体模型，但尚未形成闭环负反馈.闭环负反馈的核心在于描述系统状态与价格之间的关系，即各站点车辆利用率与价格之间的函数关系式.当站点停车利用率大于标准利用率时，该站点车辆数目过多，可降低借车服务价格吸引消费者借车，抬高还车价格降低消费者在该站点还车的可能性；反之亦然.

Pn(t)仅是显示借车服务价格，则不仅是显示还车服务价格，还是实际用车服务价格，为了不至于使消费者对于价格变动产生排斥，同时保证汽车分时租赁营运商的收入，因此对显示借车服务价格及显示还车价格进行边界限制，即

为了评价动态定价模型缓解汽车分时租赁系统不均衡的效果，引入MBE(Mean Balancing Error)，即系统整体不均衡指数[5].

3 案例分析

本文将选取EVCARD电动汽车分时租赁项目的5个特征站点进行模拟，该5个站点具有人流量大、取还车时间相对集中的特点，对本次研究具有较好的典型性.根据百度地图计算选择驾车导航获得站点距离如表1所示.各站点初始车辆和车位数如表2所示，根据初始车辆和车位数的比例来计算，初始停车位利用率均值为80%.

根据调研，每天汽车分时租赁用车时间主要集中在7:00-22:00，为简化计算，忽略22:00至次日7:00的订单.以1 h为时间段标准，则从7:00-22:00共有15个时间段，即T=15.在符合日常使用规律的前提下，选取某一天的运营情况作为案例，进行基于动态定价的自适应调度模型验证.

表1 租赁站点空间相对距离表Table 1 The relative distance between stations(km)

表2 站点初始车辆、车位分布情况Table 2 The original amount of vehicles and parking space in each station

在验证该模型可行性时，本文假定最低价格Pmin=0.4元/min，Pmax=0.8元/min；显示借车服务价格对库存水平变化的敏感性c1与显示还车服务价格对库存水平变化的敏感性c2均为1.经过模拟仿真得出不同时间段不同站点借车还车价格矩阵，如表3所示，可证明该方法具有较强的可行性.

表3 自适应调度策略价格矩阵Table 3 The price matrix of the adaptive scheduling strategy(元/min)

本文以当天订单服务价格均值与系统不平衡指数作为评判自适应调度策略模型有效性的两大标准，前者与系统盈利能力相关，后者反映系统供需平衡程度，未经自适应调度策略调整和经过自适应调度策略调整之后参数对比如表4所示.

表4 自适应调度策略模型结果对比Table 4 The results of the adaptive scheduling strategy

通过对比分析，可以看出当分时租赁服务价格在[0.4，0.8]区间内变动时，系统当天服务价格均值几乎没有变动，而系统整体不平衡指数却从0.588 6降低到0.340 5，降幅高达42%，效果显著.这表明，自适应调度策略可在不降低系统盈利能力的同时，有效缓解系统的供需不平衡指数，达到了预期效果.

本文接着分析最低价格与最高价格变动对系统效益的影响.假设最高价格Pmax=0.8保持不变，最低价格Pmin∈[0,0.6]，则系统效益参数变化情况如图3所示.可得出当最低价格上升时，系统服务价格均值越靠近最高价格，但是系统不平衡指数则先下降而后上升，在Pmin=0.3时，系统盈利能力与未采用动态定价策略时相近，但系统不平衡指数却降至0.116 2，降幅高达80%，系统不平衡现象显著改善.

图3 Pmax=0.8时，自适应调度策略模型有效性验证Fig.3 Scenario simulation whenPmax=0.8

假设最低价格Pmin=0.4保持不变，最高价格Pmax∈[0.5,1.0]，则系统效益参数变化情况人图4所示.可得出当最高价格上升时，系统服务价格均值随着升高，系统不平衡指数一直下降，但其边际效益不如降低最低服务价格.

图4 Pmin=0.4时，自适应调度策略模型有效性验证Fig.4 Scenario simulation whenPmin=0.4

4 结 论

本文建立了一套以动态定价为核心、以降低汽车分时租赁系统不平衡为目的自适应调度策略，并采用EVCARD分时租赁项目作为案例进行验证，最终得出该策略能够显著地缓解系统不平衡指数，而且在一定的价格区间内并没有降低整体服务价格均值.

本文所建立的基于动态定价的共享汽车自适应调度策略为缓解汽车分时租赁系统不平衡提供了理论基础与实践借鉴.