考虑地铁站点多方式接驳范围的接运网络配流模型
张思佳,贾顺平*,王瑜琼,李 军,张 桐
(1.北京交通大学a.城市交通复杂系统理论与技术教育部重点实验室,b.交通运输学院,北京100044;2.中国交通通信信息中心交通运输信息化标准研究所,北京100011)
0 引言
在以轨道交通为主导的大城市公共交通网络背景下,研究轨道交通站点多方式接运网络内乘客的出行选择行为,对于管理者最大化接运网络的运输效率具有十分重要的意义.
既有对轨道站点的多方式接运网络的研究中,较多学者探讨了不同接运方式的接驳范围计算方法,大多以轨道站点接运网络的RP调研数据为基础,并结合数理统计等方法确定各方式的接运范围[1-2].以上研究未从客流的角度,分析不同接运方式乘客流量的分配情况,而接运需求的分配结果对管理者工作的部署具有重要的指导意义.
既有研究中,针对轨道站点多方式接运网络的配流问题研究较少,在公共交通网络配流问题的研究中,对各方式出行广义费用的刻画中,均将出行距离或时间通过惩罚系数进行简化处理[3-4],未考虑不同出行距离或时间下人们感知的变化,以及其对出行者选择行为的影响,与实际存在较大偏差.
本文在既有研究基础上,改进了对出行广义费用中接驳时间费用的计算方法,考虑了轨道交通站点不同接驳方式的接驳范围对出行者选择行为的影响,建立基于Logit-SUE的多方式接驳网络配流模型.
1 问题描述
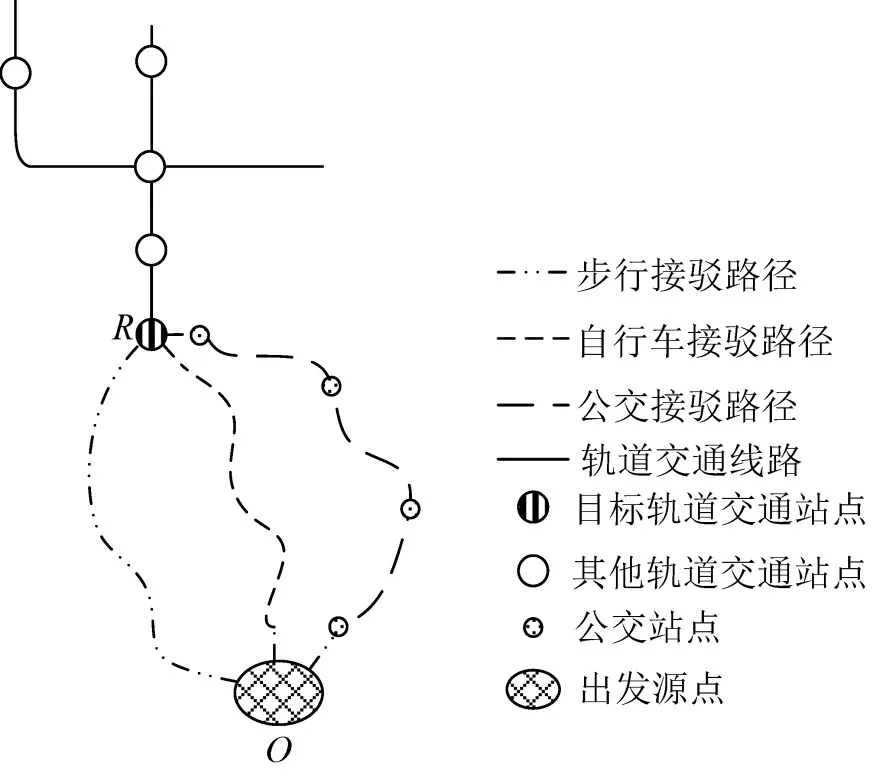
本文研究对象为接运轨道交通站点的多方式接驳网络,如图1所示.其中,R为目标轨道交通站点,O为乘客出发源点,O点与站点R的出行方式为k,k=1,2,…,m.
当乘客在接运网络中出行时,既有研究假定乘客感知到的出行费用随接驳距离增加的增长速度是定值,即不同接驳距离下人们对出行费用的感知系数是相同的.然而,在实际过程中,乘客选择某一种接运方式的出行广义费用随接驳距离增加的增长速度应随着接驳距离的增加逐渐增大,且不同接驳方式的增长速度变化规律也可能不同.
因此,本文考虑了乘客在接驳网络中,其出行广义费用随接驳距离增加的增长速度变化规律与各接驳方式接驳范围间的关系,并以此为基础建立接驳网络配流模型,分析重要参数的变化对配流结果的影响.

图1 轨道交通站点多方式接运网络示意图Fig.1 The multi-mode network for urban rail transit station
2 考虑接驳范围影响的接驳广义费用计算模型
设出行者由O点至站点R选择方式k的接驳广义费用为,分别由出行时间费用和票价费用组成,即

2.1 接驳时间费用的确定
在计算地铁站点各接驳方式出行时间费用时,出行者感知到的接驳距离增加系数不是一成不变的,应随出发距离的增加而增加,为描述此种变化规律,本文认为出行者感知到的接驳距离增加系数随出发距离的增加呈阶梯状增加,且阶梯变化的临界距离点与接驳网络中相互竞争的不同接驳方式的接驳范围有关.
设站点R步行、自行车和公交方式的接驳范围分别为lwalk、lbike和lbus,选择步行接驳方式的实际接驳距离为,时间价值为α,步行时间惩罚系数为λ1,平均步行速度为v1.

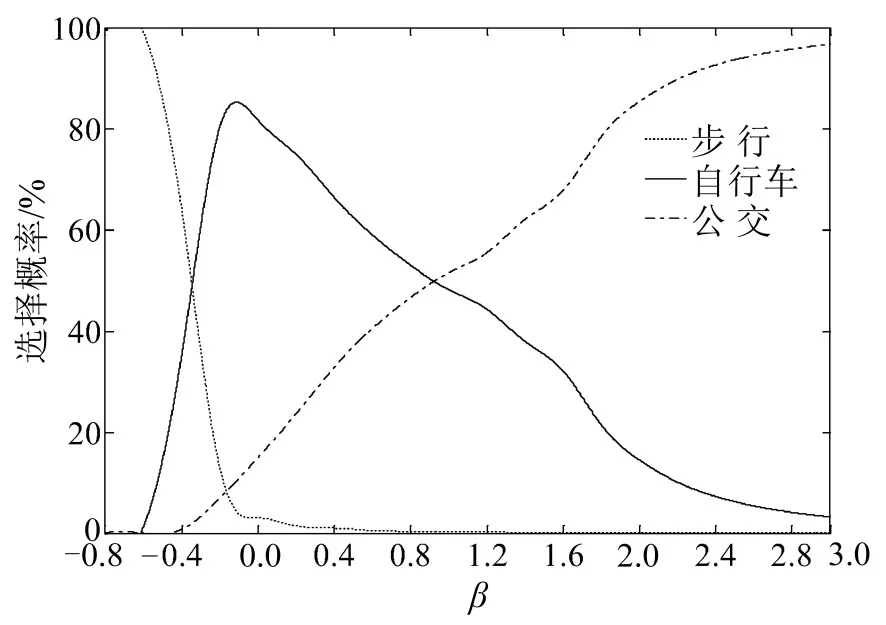
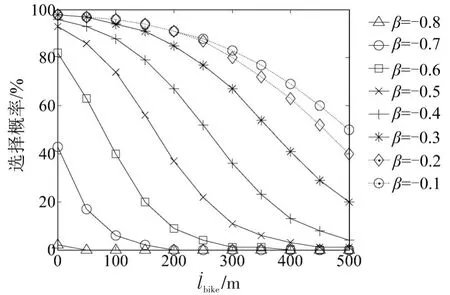
当lwalk< 对于w′1bus3,设v3为公交车辆平均旅行速度,乘车时间惩罚系数为λ4,为实际乘车距离,则有 (1)步行接驳方式. 图2 轨道交通站点多方式优势接驳范围示意图Fig.2 The advantageous ranges of multiple access modes for urban rail transit station (2)自行车接驳方式. 接驳网络中,乘客将根据自身经验选择自己认为出行费用最少的接驳方式,方式选择行为依然遵循Wardrop第一原理,设接驳方式k被选择的概率为αk,每种方式上分配的乘客数量为gk,则 运用Logit模型来描述出行者对不同接驳方式的选择概率,即当达到平衡状态时,O点与R点间被选择的接驳方式k的乘客数量gk满足 式中:θ为描述出行者对接驳网络中各路径费用的感知程度系数,θ取值越大,模型配流的随机性越小,当θ=100时,SUE配流趋近于UE配流[4]. 根据文献[4],构建基于Logit-SUE的多方式地铁接驳网络配流模型为 式(29a)第1项是对各接驳方式的广义费用函数积分求和;第2项与乘客感知相关. 为证明模型与SUE条件间的等价性,首先构造模型的广义拉格朗日函数为 可写出优化模型式(29a)~式(29c)Kuhn-Tucker条件为 式中:κ是对应于式(29b)的K-T乘子. 当gk>0时,式(31)可化简为 解得gk,并代入式(29b)中,可得到Logit模型为 选取某大城市典型住宅区中的某一聚集点为O点,以邻近O点的某地铁站点R的接驳网络为研究对象,接驳方式包括步行、自行车和公交3种,即m=3.以早高峰期间由O点接驳到达R站的通勤者群体为客流对象,接驳网络如图3所示,参考该市各接驳网络情况及收费标准,设定各出行路径基本信息如下: 公交接驳方式,l′bus为1.1 km,为0.3 km,f1为360 s,ubus为1元. 根据实地调研结果和相关文献,模型中其他参数分别为:v1=1.5 m/s[3],v2=3.3 m/s[5],v3=5 m/s[6],λ2=1.1,λ4=1.2[7],f1=6 min,lwalk=0.8 km、lbike=1.2 km和lbus=2.7 km;参考既有文献,算例中,θ=10[4],α=0.003 3元/s[8],λ1=1.3[3],λ3=1.5[3]. 图3 接驳网络示意图Fig.3 The multi-mode network in the case 4.2.1 算例结果 运用MSA算法对模型进行求解,并通过模型计算得到各接驳方式选择概率如表1所示.当接驳距离约为1.3 km时,接驳网络中,通勤者选择自行车和公交方式的概率分别为82%和15%,选择步行方式的通勤者仅为3%. 表1 模型结果比较Table1The comparisons of the results 与既有研究相比,当接驳距离约为1.3 km时,本文方法计算得到的αwalk有所减小,而αbike和αbus均略有提高.分析其原因,考虑到lwalk、lbike和lbus的范围,当接驳距离为1.3 km时,公交方式的接驳时间计算方式不受影响,自行车方式略受影响,而步行方式所受影响最大.以步行接驳方式为例,人们出行0~800 m范围内的步行时间惩罚系数为λ1,由于考虑了人们对出行时间费用感知系数随接驳距离不断增大,在800~1 300 m范围内的步行时间惩罚系数则高于λ1,因而本文方法计算得到的步行接驳方式出行广义费用与既有研究相比更大、选择概率则更小.因此,本文方法相比既有方法的αwalk、αbike和αbus分别变化-4%、+2%和+2%. 4.2.2 重要参数灵敏度分析 (1)通勤者阻抗感知系数θ. θ对各接驳方式选择概率的影响如图4所示.θ越大,通勤者对路径阻抗的感知与现实越贴近,越倾向于选择实际路径阻抗较小的接驳方式,αbike逐渐增大,而阻抗相对较大的公交和步行接驳方式选择概率则存在逐渐减小的趋势.β为接驳距离调整系数,即原接驳距离为时,调整后的实际接驳距离为,通过改变β的值来改变O点至R 图4 θ对接驳方式选择概率影响示意图Fig.4 The influences ofθon choice probabilities of multiple access modes (2)接驳距离调整系数β. 不同出行距离下各接驳方式的竞争力不同.设点的距离,得到不同接驳距离下各接驳方式的选择概率变化情况如图5所示. 从横向看,随着β的逐渐增大:αwalk逐渐降低,当β〉0.4时,即接驳距离大于1 820 m时,αwalk低于1%,基本失去竞争力;αbike先增大后减小,当β=-0.114,即接驳距离为1 152 m时,达到峰值,最大选择概率为85.2%;αbus逐渐增大,当β〉0.95时,即接驳距离大于2 535 m时,αbus大于50%. 从纵向看:当β<-0.35时,即接驳距离较短,小于845 m时,步行方式无票价且更方便的优势更突显,选择概率最大,自行车方式选择概率相对较小,而几乎没有通勤者选择公交接驳方式;当-0.35≤β≤0.93时,即接驳距离在845~2 509 m时,自行车方式以其便捷、换乘少、等待少等优势的竞争力最大,选择概率最大;当β〉0.93,即接驳距离大于2 509 m时,公交方式快速、体力消耗较小等优势逐渐突显,选择概率超越自行车方式成为竞争力最大的接驳方式. 图5 β对接驳方式选择概率影响示意图Fig.5 The influences ofβon choice probabilities of multiple access modes (3)共享单车停车位设置距离l˙bike. 研究共享单车停车位设置点距居民聚集点距离的合理范围,将为共享单车停车管理工作的开展提供有力理论支撑.假设由O点出发并选择自行车方式接驳至站点R的通勤者均选择共享单车出行,且共享单车停车位设置点距住宅区距离为l˙bike,各接驳方式选择概率随l˙bike变化情况如图6所示. 随着l˙bike的逐渐增加,αbike逐渐减小,αwalk和αbus逐渐增加.算例中的接驳距离下,αwalk始终较小,始终低于其他两种接驳方式;l˙bike对αbike和αbus的选择概率影响更大,算例中,当l˙bike〈446 m时,αbike始终最大,高于公交方式;当l˙bike〉446 m时,公交方式选择概率将超越自行车方式,成为人们接驳出行的首选. 同时,改变β的值,得到l˙bike对αbike的影响情况如图7和图8所示.一方面,无论何种接驳距离下,l˙bike增大,αbike始终减小;另一方面,β越大,l˙bike对αbike的影响程度先增加后减小,当接驳距离很短(算例中β=-0.8)或很长(算例中β=2.8)时,l˙bike对αbike几乎无影响. 图6 l˙bike对各接驳方式选择概率影响示意图Fig.6 The influences ofl˙bikeon choice probabilities of multiple access modes 此外,不同β下的l˙bike对αbike的影响规律可归纳为: ①当-0.8≤β≤-0.1时,如图7所示,接驳距离处于相对较短的范围,β越大,αbike越大.当-0.8≤β≤-0.6时,αbike随l˙bike减小的速度逐渐减小;当-0.5≤β≤-0.3时,αbike随l˙bike减小的速度先增加后减小;当-0.2≤β≤-0.1时,αbike随l˙bike减小的速度逐渐增加. 图7 l˙bike对αbike影响示意图(β=-0.8~-0.1)Fig.7 The influences ofl˙bikeonαbike(β=-0.8~-0.1) ②当β≥0.0时,如图8所示,接驳距离处于相对较长的范围,β越大,αbike越小.当0.0≤β≤1.2时,αbike随l˙bike减小的速度逐渐增加;当β≥1.6时,αbike随l˙bike减小的速度逐渐减小. 图8 l˙bike对αbike影响示意图(β=0.0~2.8)Fig.8 The influences ofl˙bikeonαbike(β=0.0~2.8) 以大城市接运轨道交通站点的多方式接驳网络为研究对象,在对接驳网络出行广义费用的计算中考虑了多方式接驳范围的影响,建立基于Logit-SUE的接驳网络配流模型,并得到如下结论,可为最大化接驳网络运营效率等提供理论依据. (1)在模型中考虑出行者对出行费用的感知系数随接驳距离变化的规律十分必要,当接驳距离约为1.3 km时,相比既有研究,αwalk有所减小,αbike和αbus均略有提高. (2)θ越大,配流结果随机性越弱,实际阻抗越小的接驳方式选择概率越大. (3)β越大,接驳距离越大,αwalk越小,αbike先增大后减小,而αbus则逐渐增大. (4)l˙bike越大,αbike越小,αbike和αwalk越大;随着β的逐渐增大,l˙bike对αbike的影响程度先增加后减小.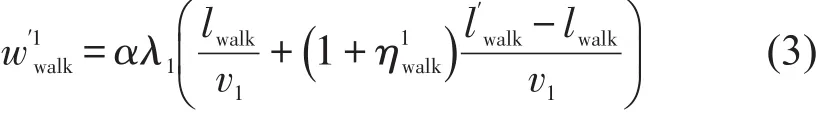






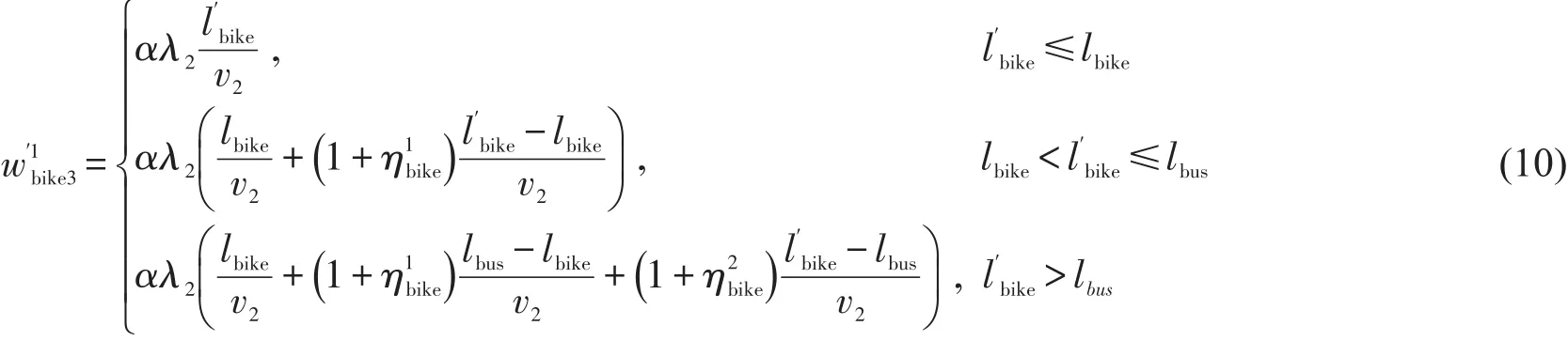

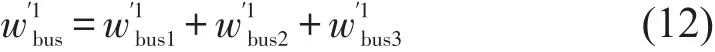


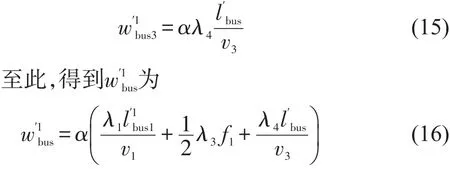
2.2 多方式距离惩罚系数的确定





3 基于Logit-SUE的多方式接驳网络配流模型

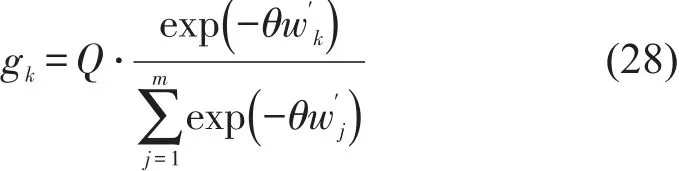
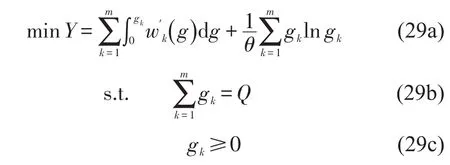


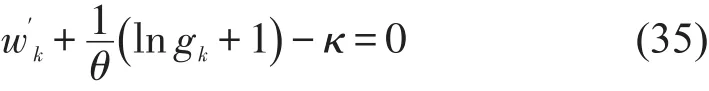

4 算例分析
4.1 算例背景
4.2 结果分析




5 结论

