通过全息图多子图再现像滤波提高全息图再现质量∗

黄晓辉，贾振红

(新疆大学信息科学与工程学院，新疆大学乌鲁木齐830046)

0 引言

数字全息目前已应用于生物医学成像[1]、计量等领域[2].数字全息图中总是包含各种噪声,如散斑噪声、CCD读出噪声等,这些噪声会严重影响获取的图像质量和信噪比[3].事实上在全息术的发展过程中，噪声始终是影响全息术发展和应用的一个重要问题.在出现数字全息之前，人们就注意到了全息图的噪声问题，Karl A.Stetson于1968年就注意到了噪声对全息图的影响，并在光学层面提出了提高全息图再现像分辨率和信噪比的方法[4].数字全息出现后，人们设法通过计算机图像处理技术减少全息图获取和再现过程中产生的散斑噪声,Jorge Garcia-Sucerquia等利用中值滤波等方法减少了再现像中的散斑噪声[5]，Akshay Sharma等则提出了通过小波变换消除再现像中散斑噪声从而提高信噪比的方法[6],蔡晓鸥等利用Wiener滤波方法降低了全息图再现像中的噪声[7].Junmin Leng等多次重现全息图并叠加，然后使用求灰度平均值的方法平滑噪声[8].这些方法都是对全息图再现像进行了去噪.Choongsang Cho使用Laplace算子有效降低了在线全息图的直流噪声[9]，侯比学等针对飞秒电子学全息选通透过散射介质成象技术,提出了通过线性变换提高全息图对比度，低通滤波后对再现的多幅再现像求平均的方法改善了最终成像质量[10],这两篇文章都降低了零级衍射斑的干扰，但没有研究针对散斑噪声的量化去噪效果.

近年来，出现了把单幅数字全息图分成多幅子全息图来降低散斑噪声的方法[11,12]，通过对这些子全息图的再现像求平均达到降噪的目的[13−15].这些方法与我们的方法相似，然而，通过这些方法获得的再现像质量仍然存在明显的噪声.

本文提出了一种对全息图多子图进行滤波提高再现像空间分辨率并降低噪声的算法.该算法是从一幅全息图中截取一定数量的相等尺寸的子全息图，然后对这些子全息图进行数字再现从而得到一定数量的再现像,并对每个再现像进行滤波处理以初步降低散斑噪声，然后对滤波后的再现像求平均得到一幅最终的再现像.这个算法的效果通过一系列实验得到验证，结果表明：这个算法能够显著提高再现像的空间分辨率，同时降低散斑噪声.

1 本文算法

本文提出的算法流程如图1所示.一幅完整全息图H(x,y)（Nx×Ny）被分成Ns个子全息图Hsn(x,y)(n=1,2,3,···Ns)，然后对这些子全息图的再现像求平均，从而得到最终的再现像，如（1）式所示.

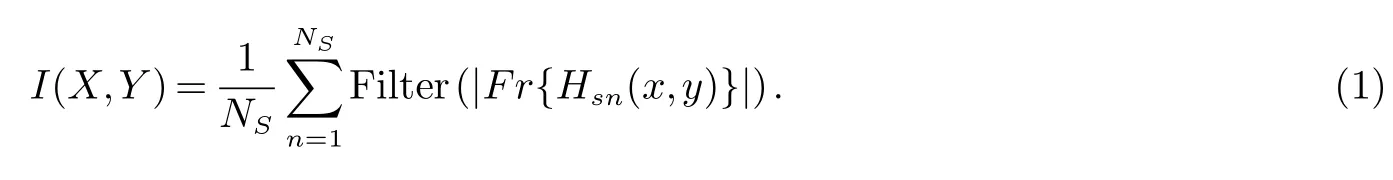
filter表示滤波函数，由于需要滤波处理的子全息再现像数量较多，所以本文使用滤波效果较好，而且运算速度较快的中值滤波器和维纳滤波器.Ns表示模板的数量，Fr{}表示菲尼尔衍射积分[13]，如（2）式所示：

U(x,y)表示复振幅分布，z是光波传播距离,k和λ分别表示波数和波长.

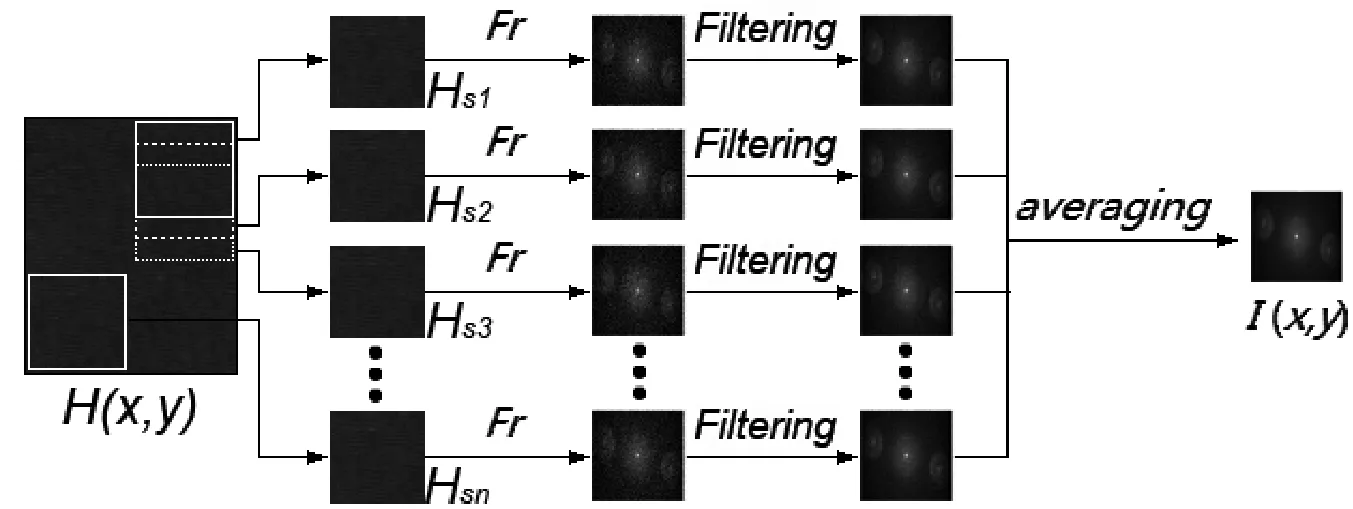
图1 本文算法流程图

全息图再现像中总是存在严重的散斑噪声，而通过滤波器滤波后可以降低噪声，但会造成有用信息的损失.由于不同再现像中散斑分布各不相同，通过大量再现像的平均可以在增加有用信息的同时，进一步降低散斑噪声.

2 实验及结果

记录全息图的实验光路图如图2所示.光源是一只半导体激光器，激光器输出的光波长为532nm，功率是50mW.用一个三棱镜将光束分成物光和参考光，参考光被透镜L1和L2组成的扩束器变成平面波，物光被透镜L3扩束后照射物体.M1、M2和M3是全反镜.全息图由一台CMOS相机(Basler ace acA3800-14uc，分辨率：3 840×2 748 pixels，像元尺寸：1.67µm)记录.相机感光面与物体之间的距离是970 mm.

为了验证算法的有效性，我们用图2所示的光学装置记录了多幅数字全息图.全息图使用菲尼尔再现算法再现，再现距离均是970mm，并记录了所有再现像中虚像的位置和大小.为了便于比较，实验中分别使用中值滤波器和维纳滤波器，并与单幅全息再现像及经过滤波的单幅再现像进行了比较.实验结果从视觉效果和定量指标两方面分析，这里定量指标指的是散斑指数(SI)和等效视数(ENL)[16].

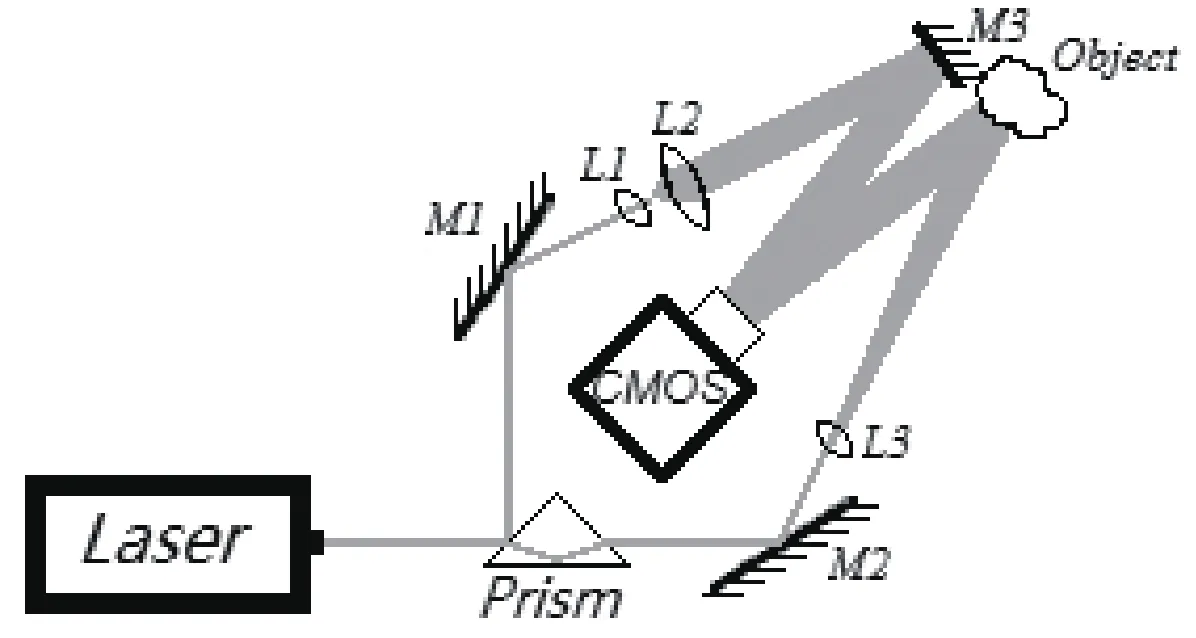
图2 记录全息图的光路图

图3(a)显示了一幅全息图(3 840×2 748 pixels)，图3(b)是图(a)的再现像(3 840×2 748 pixels).图3(c)是从图3(b)中截取的聚焦虚像（原图754×754pixels，为了便于排列缩小至281×281 pixels）.使用一系列空间域模板与全息图相乘得到了476个子全息图（1 024×1 024 pixels），在x和y方向上相邻子全息图之间间距都是100 pixels.图3(d)(281×281 pixels)是图3（c）经维纳滤波后的再现像，图3(e)-(f)(281×281 pixels)是使用本文提出的算法得到的再现像.本算法的滤波部分，图3(e)使用了中值滤波器，图3(f)维纳滤波器.从视觉效果来看，显然，图3(e)-(f)与图3(c)-(d)相比有更高的图像分辨率,且散斑噪声明显降低.图3(e)与图3(f)的分辨率和噪声水平相当.图3(d)与图3(c)相比散斑噪声有所降低.

表1给出了散斑指数、等效示数和计算时间等数据.散斑指数是对图3(c)-(f)整图计算的，等效视数是使用3(c)-(f)中左上角的矩形区域中灰度值计算的.从散斑指数来看，使用本文算法所得图像散斑指数明显较低，说明图像中散斑噪声得到了有效抑制.而本算法中使用维纳滤波比使用中值滤波散斑指数要小一些，说明使用维纳滤波更有利于降低散斑噪声.从表中数据还可以看出，使用维纳滤波器能使单幅全息图再现像的散斑指数明显降低，说明维纳滤波可以有效抑制散斑噪声.从等效视数来说，使用本文提出算法所得再现像的等效视数明显高于单幅再现像和经过滤波的单幅再现像的散斑指数，说明本文算法可以使全息图再现像更加平滑.从运算时间来看，本文提出的算法时间较长，主要是因为计算大量的全息图再现像需要花费更长的时间.

图3 全息图及其再现像

表1 散斑指数、等效视数和运算时间

图4是对另外三幅全息图处理的结果，散斑指数、等效视数和耗费时间等数据如表2所示.从结果可以看出，本文提出的算法在提高再现像分辨率方面效果明显.从等效视数指标来看，使用本文提出的算法得到的再现像比单幅再现和经过维纳滤波的再现像等效视数高很多，说明噪声被有效抑制.从散斑指数来看，本文算法所得再现像比单幅再现像和经过滤波的再现像要低.这些结果证明了本文提出的方法是可靠的.

图4 （a）、（e）和（i）分别是三幅全息图再现像中的虚像部分，（b）、（f）和（j）分别是图（a）、（e）和（i）经wiener滤波后的图像.图(c)、(d)、(g)、(h)、(k)和(l)(均为281×281 pixels)是使用本文提出的算法得到的再现像.在本算法的滤波部分图（c）、（g）和（k）使用的是中值滤波器，图（d）、（h）和（l）使用的是维纳滤波器

表2 散斑指数、等效视数和运算时间

3 结论

本文提出了对全息图多子图进行滤波提高全息图再现像分辨率并降低散斑噪声的算法，通过多项实验证明该算法的有效性.实验结果表明使用该算法可以显著提高全息图再现像的空间分辨率，同时降低了散斑噪声.本算法中分别使用了两种滤波器，其中使用维纳滤波器得到的效果较好，但运算时间稍长.具体使用时可以根据需要选用其中一种.