应用HYDRUS-1D模型模拟分析PFCs在土壤中的迁移特征

邰托娅，郑跃军*，王金生

（1.中国地质环境监测院，北京 100081；2.北京师范大学水科学研究院，北京 100875）

全氟化合物（Perfluorochemicals，PFCs）是分子中与碳原子连接的氢原子完全被氟原子所取代的一类由人工合成的有机化合物，由于其优良的化学稳定性和表面活性被广泛用于化工、纺织、造纸、包装、涂料、皮革、农药、合成洗涤剂、灭火泡沫等与生产生活关系密切的产品中。这类产品的大量使用，使得PFCs以多种途径进入到环境中，并通过食物链传递和生物富集作用，对人体和动物体健康造成危害[1-2]，2009年联合国环境规划署正式将全氟辛烷磺酸及其盐类列入新的持久性有机污染物，要求减少并最终停止生产和使用该类物质。

土壤是PFCs在环境中重要的源和汇，PFCs能够通过点源污染、大气干湿沉降、地表径流等进入土壤[3-4]，而进入到土壤中的PFCs，一部分可能会通过蒸发、扩散、淋溶和雨水冲刷等方式进入大气、地表水[5]，而另一部分会通过包气带进入地下水，对地下水环境造成危害，然而，目前有关环境介质中PFCs的研究主要集中于流域地表水[6-8]以及沉积物中[9-11]，研究内容也多集中在PFCs的分析检测技术[12-13]和分布特征方面，仅有少数研究对PFCs在沉积物或土壤中的吸附行为做过探讨[3，9，14]，而关于 PFCs在土壤中迁移转化的研究更是鲜有报道。大量研究表明，吸附作用是PFCs在土壤中迁移的主要机制，因此研究基于吸附作用下的PFCs在土壤中迁移规律具有十分重要的现实意义。

数值模型可以模拟污染物从地表进入地下水的运移过程，并对运移过程中的影响因素做出分析，是地下水污染防治的重要方法。本研究采用HYDRUS-1D模型，基于经典对流弥散方程，建立主要考虑吸附作用的数值模型，模拟典型全氟化合物在土壤中的运移分布规律，并用一维土柱实验结果来验证HY⁃DRUS-1D模型模拟结果，通过对比评价模型模拟效果，并进行参数敏感度分析，确定影响数值模拟的主要参数，以更加深入地了解全氟化合物的污染运移特征。

1 材料与方法

1.1 室内土柱实验方法

供试土壤主要采自辽宁省辽中市黑山县某处林地，采样深度为30 cm，进行实验前，首先将采集的土壤样品自然风干，去除植物残体、根须及砾石等杂质，混匀研磨后过1 mm筛备用。分析土壤中的有机质含量为0.143%，黏粒含量为0.1%，容重1.21 g·cm-3，pH值为5.23。

室内土柱装置选用有机玻璃管为渗流实验的外壁，内径10 cm，高50 cm，在顶盖和底盖中心位置分别设置直径为1.5 cm的小孔进行进水和出水，淋溶液为目标PFCs混合溶液，浓度为2 mg·L-1，流速为2 mL·min-1，每淋溶24 h在出水口进行一次取样测试。

本研究选取6种PFCs作为研究对象，分别为全氟丁酸（PFBA）、全氟己酸（PFHxA）、全氟庚酸（PFH⁃pA）、全氟辛酸（PFOA）、全氟壬酸（PFNA）和全氟辛基磺酸（PFOS），采用Waters超高效液相色谱/电喷雾串联质谱仪进行分析测定。

1.2 模型的建立

HYDRUS-1D软件[15]是一套用于模拟饱和-非饱和多孔介质中水分运移和溶质运移的数值模型，适用范围广，操作简便，在土壤水分氮素运移[16-20]、土壤污染物运移[21]、地下水污染风险评价[22]方面得到了广泛运用。

本文采用HYDRUS-1D建立土壤水流和溶质运移数值模型，主要模拟PFCs随入渗溶液进入土柱后的迁移过程，定量描述水流运动和溶质在运移过程中发生的反应，设定时间单位为d，质量单位为mg，长度单位为cm。根据土柱实验的运行情况，将模拟时间定为24 d。

土柱初始压头为-50 cm。假设土壤为均质且各向同性。对于水流模型，设置上边界为定通量边界，将下边界设为自由排泄。对于溶质模型，初始土壤水溶质浓度为0，上边界为通量边界，下边界选择零梯度边界条件，计算土壤水渗漏量和PFCs淋出量。

（1）土壤水流模型的建立

本模拟中水流模型概化为均质各项同性饱和一维垂向稳定流，不考虑作物吸收和植被蒸腾作用，主渗流方向向上为正，向下为负。一维平衡水流运动采用Richards方程来描述：

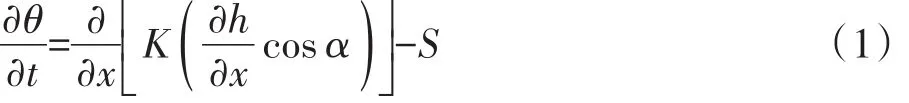
式中：h为压力水头，cm；θ为土壤体积含水率，cm3·cm-3；t为时间，d；S为源汇项，cm3·cm-3·d-1；α为水流方向与纵轴夹角，本研究取α=0；K为饱和渗透系数，cm·d-1。

初始条件：

上边界条件：

下边界条件：

式中：h0（x）表示土壤剖面初始土壤水负压，cm；qs表示地表水入渗量，cm·d-1；hb（t）表示下边界压力水头，cm。

（2）溶质迁移模型的建立

本次数值模拟根据实验条件，考虑了土壤介质对6种PFCs的线性吸附作用及水动力弥散作用。建立溶质运移方程如下：

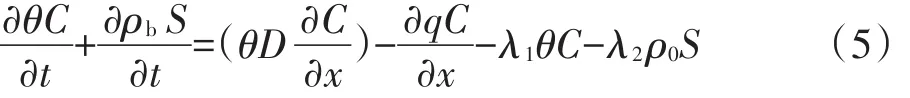
式中：C为溶质浓度，D为弥散度，q为达西流速，λ1、λ2为溶质的液相和固相降解系数，ρ0、ρb为流体密度，其他同式（1）。

根据溶质运移方程，确定模拟的初始条件和边界条件如下：

初始条件：

上边界条件：

下边界条件：

式中：C0为PFCs在土壤中的液相初始浓度，Cs表示上边界流量的PFCs浓度，mg·L-1。

1.3 模型参数获取

本模拟中需要的参数有土壤水力特征参数和溶质特征参数，土壤水力特征参数主要指水分特征曲线、饱和渗透系数、饱和水分扩散率等；溶质特征参数主要指纵向弥散度、吸附系数等。

（1）土壤水力特征参数

土壤水力特征参数的确定是研究土壤水分运移的基础，HYDRUS软件中的UNSODA数据库包含了常见的砂土、粉土、黏土等土壤介质类型相关参数，可利用人工神经网路技术建立起土壤水分特征曲线与土壤颗粒分析数据的函数关系。因此，本次模拟基于土壤颗粒组成以及土壤容重等分析数据，利用HY⁃DRUS预测土壤介质的饱和渗透系数KS和土壤的水分特征曲线参数土壤饱和含水量θS、残余含水量θr、进气值α以及特定参数n，得到结果KS为483.91 cm·min-1，θS为 0.383 5，θr为 0.044，α 为 0.038 8 cm-1，n 为2.888。

（2）纵向弥散度

纵向弥散度是表征在一定流速下，多孔介质对污染物垂向弥散能力的重要参数，可通过实验测定污染物的穿透曲线来获取，纵向弥散度的表达式为：

式中，U0.16、U0.5、U0.84分别为土柱出水口示踪剂相对浓度C/C0分别为0.16、0.50、0.84时流出液体的总体积。

在室内土柱模拟装置中，以Br-作为示踪剂，在饱和一维稳定流条件下，以一定流速淋滤KBr溶液，并在土柱出口端定时测定流出液中Br-的浓度，获得Br-穿透曲线（图1），记录流出液的体积，通过拟合得到弥散系数。从图1可以得到土柱的U0.16为565.71 mL，U0.5为1 039.00 mL，U0.84为1 265.67 mL，αL为58.94 cm。

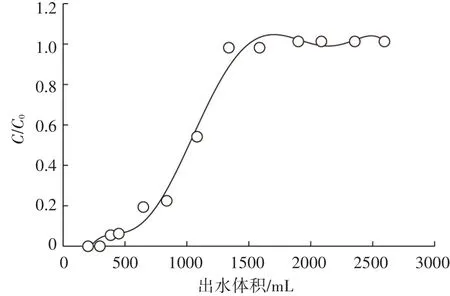
图1 穿透曲线Figure 1 Breakthrough curve

（3）等温吸附系数

吸附系数的确定由室内实验获得，本研究中6种PFCs在土壤中的吸附行为符合Henry等温线性吸附，吸附系数Kd见表1。

表 1 PFCs在土壤中的吸附系数（L·kg-1）Table 1 Sorption coefficients of PFCs in the analysed soil（L·kg-1）

2 结果与讨论

2.1 模拟结果与实验结果验证

以6种PFCs的动态淋滤实验条件为基础，采用HYDRUS-1D模型模拟PFCs在土柱出水中的含量分布，模拟值和实测值对比见图2。可以看出随着淋滤时间的推移，土柱出水口中PFCs的浓度逐渐上升，并最终在一定的浓度水平上达到稳定状态。此变化过程可分为初始吸附、快速吸附和吸附饱和3个阶段。在初始吸附阶段，淋出液中污染物质含量微小，说明土柱运行初期为强吸阶段，渗入液中PFCs被土壤介质完全吸附，且主要在土柱表层累积，淋出阶段大小由土壤介质对PFCs的吸附容量所决定；快速吸附阶段为土壤介质吸附PFCs的阶段，随着入渗量的增加，PFCs以较快的速度向下层土壤迁移，说明渗入液中PFCs部分留在土壤中，部分下渗排出，淋出液中PFCs含量逐渐升高，显然，快速吸附阶段的大小决定了污染物质能否通过包气带污染地下水，它取决于介质的吸附强度及吸附速度；吸附饱和阶段，土壤已无吸附净化能力，即土壤介质对PFCs的吸附达到饱和状态，淋出液中污染物质含量变化较小，达到平衡稳定状态。

2.2 误差分析

为了检验模型的模拟效果，将模型模拟结果与实验测得结果进行对比拟合，结果见图3，可以看出R2均在0.96以上，说明HYDRUS-1D模型可以很好地模拟PFCs在土柱中的运移情况。

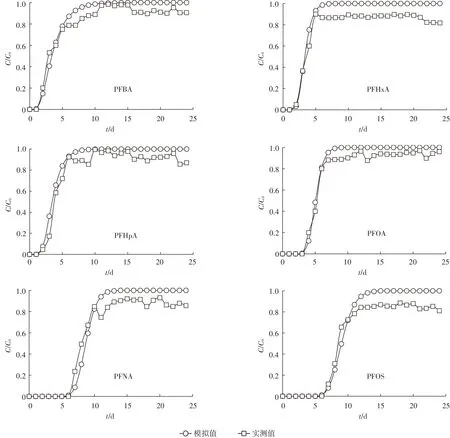
图2 PFCs在土壤中迁移的实测值与模拟值比较Figure 2 The measured value and the simulated value of PFCs in the analysed soil

采用RMSE来表征模型拟合程度，即模拟值和实测值的偏差程度，SSE越接近于0，说明模型选择和拟合更好，数据预测也越成功。RMSE计算公式见式（10），计算结果见表2。

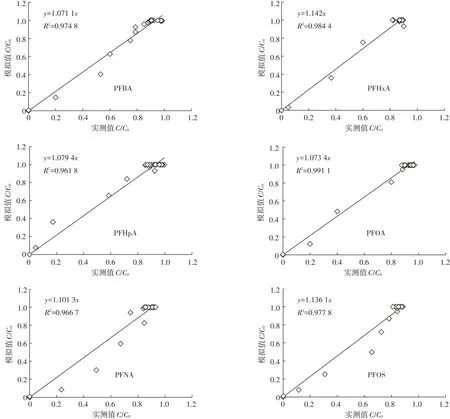
图3 模拟值与实测值偏差分析Figure 3 The error analysis of the measured value and the simulated value

从表2可以看出，6种PFCs的RMSE值的范围在0.06～0.12之间，说明模拟结果较好，从图2中可以看出，HYDRUS-1D模拟值与实测值拟合程度较好，模拟结果中C/C0对应的时间与实测值较吻合，模拟结果反映了几种PFCs在土壤中的运移特征。但是在PFCs到达平衡阶段后，各PFCs的峰值C/C0在0.82～0.97之间，平均为0.90，接近于1但小于1，实验测定的浓度会略低于模拟值，二者并不能完全重合，这是因为HYDRUS模型考虑的是一种比较理想的情况，即PFCs在穿透土柱后的浓度与初始淋滤浓度相同，而实际情况下，PFCs在土壤中的运移是个复杂的过程，土壤对PFCs有一定的吸附和截持作用。首先，在PFCs的分子结构中，C-F键有较强的疏水性，且随着C链的增长，分子量的增加，PFCs的疏水性也会增强，因此6种PFCs中，分子量较大的PFNA和PFOS更容易在土壤中滞留；其次，土壤的性质对PFCs的吸附能力也有很大的影响，研究表明[23-24]，土壤有机碳含量是决定土壤对有机污染物吸附量大小的关键性因素，二者呈线性关系，含碳物质是PFCs在土壤中吸附的一个重要的动力。PFCs在土壤上的吸附机制主要表现为PFCs在土壤中有机质和水之间的分配作用，疏水性效应和土壤有机质含量对吸附过程产生了决定性影响。本研究中土壤有机质含量较低，为砂质土壤，因此吸附平衡后PFCs被土壤吸附的部分也会相对较低，这也是C/C0接近于1的原因之一。此外，PFCs虽然属于一类难挥发的有机污染物，且在实验的过程中已最大程度减小生物降解作用对PFCs迁移的影响，但在与土壤作用的过程中，不仅存在土壤对PFCs的吸附作用，还会发生其他的物理化学作用和生物作用。因此，平衡浓度的实测值与模拟值会有一定的偏差，还需对PFCs的运移机制进行深入研究。

表2 6种PFCs的RMSE值Table 2 The RMSE of PFCs

2.3 参数敏感度分析

参数敏感度分析是将待考察参数增加或减少适当的数量进行模型模拟计算，观察其对模拟结果和目标函数变化的影响程度。引起目标函数改变越大的参数越敏感，反之亦然[25-26]。

影响PFCs在土壤中迁移转化的因素包括对流弥散作用和化学反应。对流弥散过程主要影响参数为土壤颗粒组成、入渗水量、土壤孔隙度及渗透性，化学反应考虑了PFCs的吸附作用，主要参数为吸附系数。因此，本研究以环境中检出率较高的PFOA为例，采用单因素局部扰动分析方法[27]，分别对HYDRUS-1D模型中入渗水量、土壤容重、纵向弥散度和吸附系数进行扰动（扰动幅度为±20%，±40%），并与参数原值结果进行相比。研究参数变化对PFCs在土柱中穿透时间的影响，旨在找到敏感性较强的模型参数，确定对迁移过程影响显著的主要因素。

为了更好地说明和比较PFCs在土壤介质中的运移特征，本研究将以t0.5作为表征PFCs在土壤中穿透能力大小的指标，t0.5表示淋出液中PFCs浓度为初始浓度50%（C/C0=0.5）时对应的时间，所需的t0.5越大，PFCs在土壤中的迁移能力越小。

敏感系数Sji可由下式计算：

式中：Sji为函数Fj（X）对变量xi的灵敏程度，Sji越大，说明变量xi越灵敏，对函数的影响也越大。在本研究中，Fj（X）表示t0.5的变幅。

（1）入渗水量

污染物随着入渗水量进入到土壤中，并同土壤发生一系列的反应。以PFOA为例，分别增加和减小幅度20%，得到不同入渗水量变幅条件下PFOA在土柱中的穿透曲线图（见图4）。可以看出，随着入渗水量的增加，t0.5减小，即入渗水量越多，PFOA进入到土柱中的量越多，所用的穿透时间越短。

（2）土壤性质

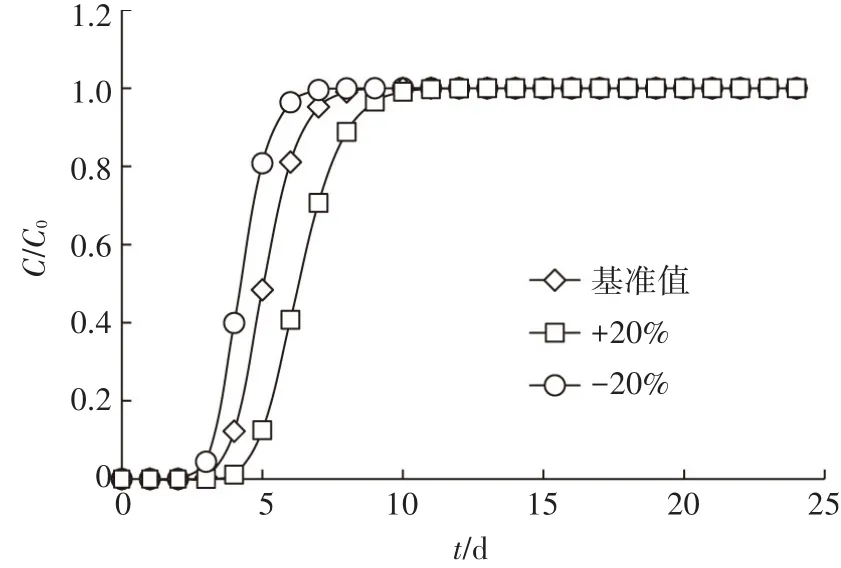
图4 不同入渗量条件下PFOA穿透曲线图Figure 4 The breakthrough curve of PFOA in different infiltration conditions

土壤介质性质为PFCs在土柱中发生各类反应提供了相应的环境和条件。在HYDRUS模型中，分别改变饱和土壤含水率、饱和渗透系数和土壤容重的变化幅度，结果与t0.5的关系见图5。可以看出，饱和含水率和饱和渗透系数随着各自的变幅引起的t0.5的变化很微小，即饱和含水率和饱和渗透系数对PFCs的迁移并没有太大的影响，而土壤容重的减小，会使t0.5明显的减小。这说明土壤容重与t0.5的关系相比其他两种因素更加敏感。

（3）纵向弥散系数

以PFOA为例，纵向弥散系数分别增加幅度为20%、40%，和减小幅度为20%、40%时PFOA在土壤中的穿透曲线见图6。可以看出，不同纵向弥散度变幅下，浓度穿透曲线的变化趋势一致，且接近于重叠，说明纵向弥散度对t0.5的敏感度较小。

（4）吸附系数

以PFOA为例，将吸附系数分别增加幅度为20%、40%，和减小幅度为20%、40%时，穿透曲线变化见图7。随着吸附系数变化幅度的增加，t0.5越来越大，说明随着吸附系数的增加，PFOA被土壤吸附的量越多，反应越复杂，与土壤作用的时间也越长。从图3～图7中可以看出，入渗量、土壤容重和吸附系数的变化对PFOA在土柱中运移影响较大。

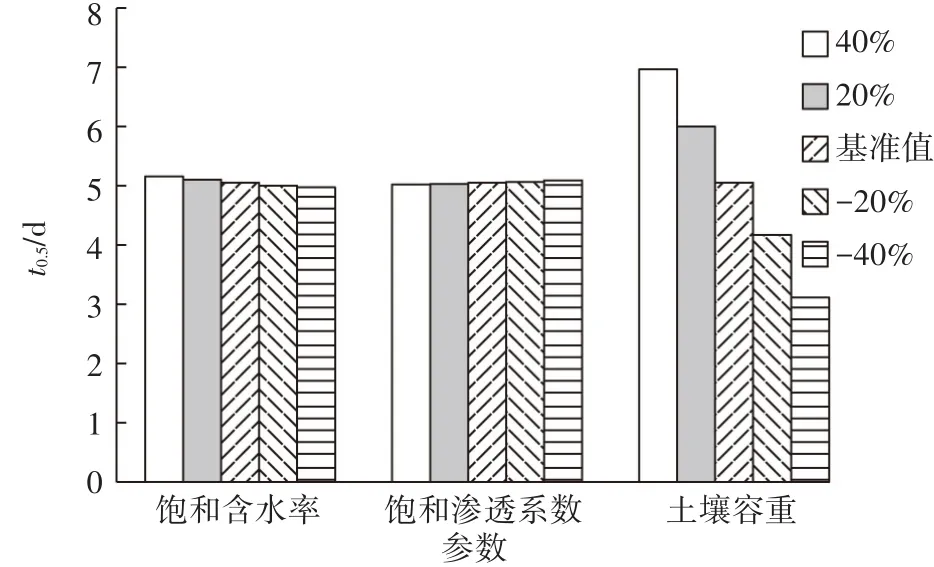
图5 土壤性质变化与穿透时间关系图Figure 5 The breakthrough time of PFOA in different soil conditions

图6 不同纵向弥散系数条件下PFOA穿透曲线图Figure 6 The breakthrough curve of PFOA in different longitudinal dispersion conditions

分别计算6种PFCs入渗水量、饱和土壤含水率、饱和渗透系数、容重、纵向弥散系数和吸附系数对t0.5的敏感系数，见表3。

通过表3可以看出，吸附系数和土壤容重是模型中最为敏感的参数，敏感系数为0.937～0.977。其次是入渗水量，敏感系数为0.813～0.833。饱和土壤含水率、饱和渗透系数和纵向弥散度敏感度较小，敏感系数分别为0.033～0.062、0.005～0.021和0.002～0.084。其中，与t0.5正相关的参数有入渗水量、饱和渗透系数和纵向弥散度，与t0.5负相关的参数有饱和土壤含水率、容重和吸附系数。这说明，在室内小尺度土柱实验模拟PFCs的迁移过程中，污染物的淋溶量、土壤的孔隙度以及污染物本身的吸附能力是决定污染物迁移能力大小的主要影响因素。PFCs的淋溶量越大、吸附系数越大、土壤的孔隙度越高（容重越小），PFCs在土壤中富集及穿透的能力就越强。

3 结论

（1）采用HYDRUS-1D模型对实验土柱出水口6种PFCs的浓度变化情况进行数值模拟，以PFCs在土柱中的运移分布实验结果为基础对模拟结果进行验证并进行误差分析，结果表明模拟值与实测值能够较好的吻合，模拟结果基本反映出了PFCs在土柱中迁移的特征。

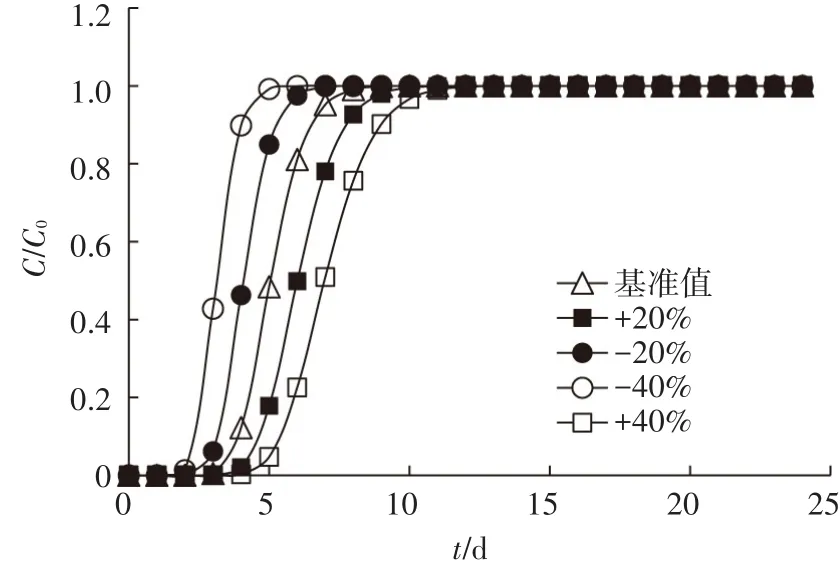
图7 不同吸附系数下PFOA穿透曲线图Figure 7 The breakthrough curve of PFOA in different Kd

（2）采用局部灵敏度分析方法对模型参数敏感度进行分析，结果表明入渗水量、土壤容重和PFCs的吸附系数是影响PFCs在土壤中迁移的主要因素。

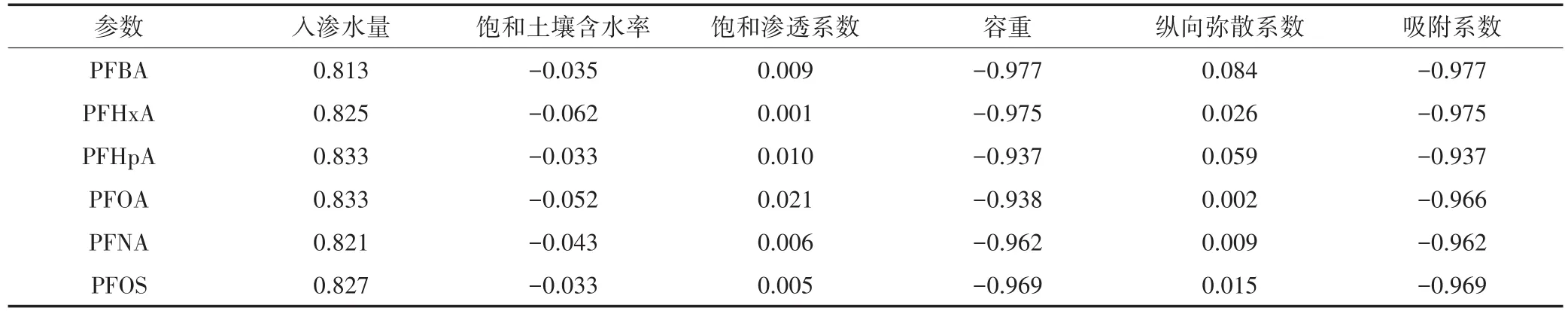
表3 敏感系数表Table 3 Sensitive coefficient