液滴撞击圆柱内表面的数值研究∗

李玉杰黄军杰肖旭斌

1 引 言

液滴是自然界中随处可见的,它在工业当中的应用也十分广泛,例如喷涂、印刷工艺、内燃机蒸发过程、涡轮叶片冷却等都牵涉到液滴撞击固体表面的现象[1−4]．液滴撞击动力学的研究也受到广泛关注,尤其是对液滴撞击固体表面的流体动力学特性的研究．范瑶[5]在对液滴撞击低温金属壁面行为特性的研究中对圆柱壁面曲率、过冷度和浸润性不同的情况进行实验,得到随曲率增加轴向液膜铺展较差,周向液膜铺展较好;液滴在低温壁面的回缩过程中会出现底层结冰现象;低温壁面接触角越大液滴振荡越明显、持续时间越长等结论．

液滴撞击过程需要考虑惯性力、黏性力、表面张力、被撞击体表面物性等因素的影响,因此,液滴撞击后液滴状态的模拟并不容易[6]．近几年,计算机技术得到了很大的提高,在此基础上液滴撞击问题的数值模拟得到很大的发展．李彦鹏和王焕然[7]在总结前人经验的基础上,用水平集和浸没边界法结合对液滴低冲击能量撞击球面的沉积特性进行了系统、全面的研究,指出沉积过程中液滴铺展面积会随球面(凸曲面)曲率半径、液滴撞击速度的变化而变化;阐述了撞击全过程中液滴在球面呈现的状态为铺展、回缩、再铺展、再回缩、沉积,在沉积过程中会出现中心局部破裂现象,且对中心局部破裂现象进行了定性分析．Huang等[8]基于捕捉界面的相场理论,采用格子Boltzmann方法(lattice Boltzmann method,LBM)模拟液滴撞击圆球的现象,研究了不同接触角、动力黏性比、相对半径下液滴的变形．Shen等[9]选用Shan-Chen LBM对液滴撞击曲面进行了数值模拟研究,揭开了液滴撞击管表面会出现移动、蔓延、成核、滴下和飞溅的过程．刘邱祖等[2]基于LBM将液滴沿壁面的铺展简化为液膜流动问题,考虑固-液分子间的作用力,分析了壁面润湿性、液滴表面张力对铺展动态的影响．宋云超等[10]采用复合水平集-液体体积(coupled level-set/volume-of- fluid,CLSVOF)方法研究液滴撞击壁面发生的飞溅运动,建立了发生飞溅运动临界条件的理论模型,并给出相应的判据判断撞击后是否会发生飞溅现象．上述研究工作就液滴撞击平面或凸曲面现象给出理论分析和数值模拟,也有部分学者对该现象进行了实验研究,但对于液滴撞击凹曲面的研究尚较少．郑志伟等[11]使用CLSVOF方法分析了液滴撞击球形凹曲面的问题,凌俊[12]同样使用CLSVOF方法分析了液滴撞击凹壁面的动力学特性,并进行了一些实验研究．但对于不同数值方法和一些参数在模拟此类问题中的影响还需更加全面深入的探讨．

本文就液滴撞击圆柱内表面(凹曲面)现象,采用基于相场的LBM进行数值模拟,对液滴撞击后的动态变形等进行研究,观察了不同撞击参数、液滴物性和圆柱内表面(凹曲面)特性变化时,撞击过程及液滴形态的变化,并观察了重力的影响．

2 理论模型和数值计算

对两种不混溶流体的模拟,本文采用基于相场的混合格子Boltzmann有限差分法[13],界面动力学的Cahn-Hilliard方程(CHE)选择二阶有限差分进行空间离散及四阶Runge-Kutta法进行时间推进,流体动力学采用LBM模拟[13−15]．

2.1 相场模型

两相流的自由能泛函F可以表示为

其中,ψ(ϕ)是体积自由能密度,常用双阱形式表示,ψ(ϕ)=a(ϕ+1)2(ϕ−1)2,a为常数,序参数ϕ的变化范围为[−1,1]．(1)式中右侧第二项是界面能密度．化学势µ由F关于ϕ的变分得到

其中,常数a及界面能常数κ与界面张力σ和界面厚度W相关,有平衡状态下序参数沿界面法向由双曲正切函数描述是沿着垂直界面方向的坐标,ς0是ϕ=0处的坐标．考虑对流项,可得到序参量ϕ的演化方程(CHE):

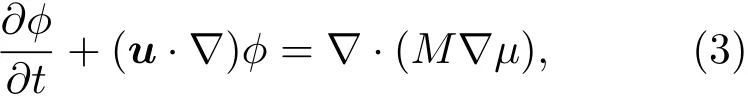
其中,M是扩散系数,为常数;u是流体速度．

当使用单松弛时间碰撞模型时,格子Boltzmann方程(LBEs)为[14,15]

其中,分别是沿着格子速度ei的分布函数和平衡分布函数(i=0,1,···,b);cs为格子声速;

uα表示速度在α方向的分量;动力黏性η与松弛参数τf相关,有．平衡分布函数为

其中,ωi是沿着格子速度方向的权重,p是动水压．本文采用常见的D2Q9格子速度模型(b=8)[16].宏观变量的计算如下:

通过Chapman-Enskog分析,可以发现上述LBEs在宏观尺度近似下列方程:

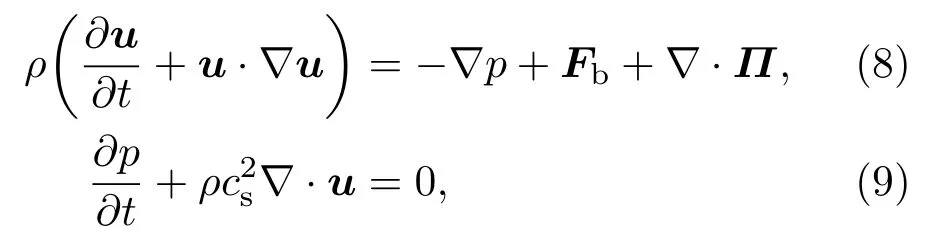
其中,Π是牛顿流体的黏性应力张量;(8)式右侧第二项Fb=Fs+Fe,Fs=−ϕ∇µ反映了表面张力的作用,Fe为外加体积力(考虑重力时Fe=ρg(g为重力加速度),否则为零).为了提高稳定性,本文采用多松弛时间碰撞模型[13,16].

2.2 边界条件

壁面附近边界条件与润湿性和接触线的运动密切相关,对于化学势µ在S表面采用无通量边界条件:

其中nw表示表面的单位法向量(指向流体).对于序参数,有各种类型的润湿性边界条件,如表面能类型、几何类型等,描述也不同[17,18].本文选择几何类型润湿边界条件(wetting boundary condition,WBC),假设在扩散界面中ϕ的等值线相互平行,包括在表面附近区域.在保证当地接触角与指定值的匹配上,几何WBC更优于表面能类型[19].具体而言,本文采用一种最近开发的基于特征插值的WBC,该方法通过充分利用序参数的双曲正切函数分布,在曲面附近无需采用复杂的插值计算,也无需判断界面和网格的相对构型,实施起来较为方便,其准确性也已得到验证[8].

2.3 物理模型

本文主要研究平面内液滴撞击圆柱内表面的过程.液滴撞击后会出现铺展、收缩、反弹、飞溅等现象[6].重力在和液滴有关问题中的重要性通常用Bond数Bo=ρLr2g/σ衡量(ρL为液体密度,r为液滴半径).在地球表面,取重力加速度g≈9.8 m·s−2,对于通常状况(1标准大气压、20◦C)下直径为1.5 mm的水滴,Bo≈0.08.由Bo数定义可见,其大小正比于液滴尺寸的平方.因此,对于尺寸较小、表面张力较大的液滴及在微重力情形下可忽略重力的影响.本文大部分研究没有考虑重力,对于重力对结果的影响本文也有涉及,具体见3.6节.为节省计算时间,本文取右半部分[20],如图1所示,上下边界采用周期边界,左边界为对称轴,右边界也使用对称边界条件(可由问题的对称性和周期性推出),圆柱内表面为固壁.r为液滴半径,UImp为液滴初始速度,R为圆柱半径.液滴中心位于(xcd,ycd),圆柱中心为(xcy,ycy).

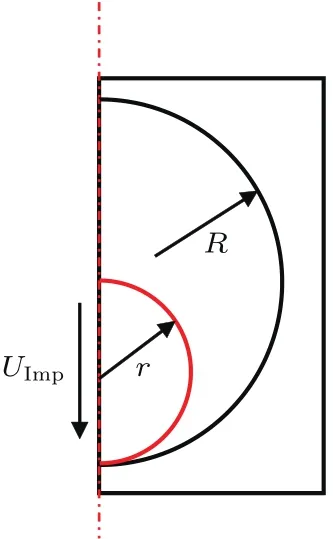
图1 液滴撞击圆柱内表面示意图(右半侧区域)Fig.1.Con figuration for the droplet impinging on the inner surface of a cylinder(right hemi area).

3 结果与分析

研究液滴撞击圆柱内表面问题涉及的因素较多,本文按如下方式定义一些物理参数,并在计算过程中选择适当的计算参数.选取初始液滴半径r作为参考长度,Lr=r.参考速度可由表面张力σ和(液体)动力黏性ηL(ηL=ρLνL,νL为液体运动黏性)导出,Ur=σ/ηL=σ/(ρLνL),由此可得参考时间Tr=Lr/Ur=(LrηL)/σ=rρLνL/σ.将参考长度Lr用NL个网格离散,参考时间Tr用NT个时间步离散,可得到网格尺寸和时间步长为δx=Lr/NL和δt=Tr/NT. 在LBM计算中常采用格子单位,可得格子速度c= δx/δt.在两相流的模拟中增加两个数值参数:Cahn数Cn=W/Lr=(W/δx)/NL和用来测量CHE中扩散相对于对流大小的Pelect数Pe=UrL2r/(Mσ).下面的模拟中,Pe数为5000,Cn值会根据NL(本文中NL=Nr)变化而有相应的变化. 选择Nr=20,40,60和80时液滴沿圆柱内表面的铺展系数进行分析,定义铺展系数Rx=xmax/r(xmax通过捕捉界面ϕ=0与壁面交汇处坐标得到,见图2(a)).由图2(b)可得,当Nr>20时,铺展系数Rx随网格数的增加变化很小[21],因此本文取Nr=40.一般而言,模拟中优先选择足够小的Cn值来接近尖锐界面的极限[22],即Cn值应尽可能小.因此,在给定Nr的情况下应使格子单位的界面厚度W/δx较小,但该参数太小会导致界面上ϕ的轮廓不能被精确捕捉,本文将该参数设置为W/δx=4,充分解决了捕捉ϕ的轮廓问题,也保证了计算成本[8].

首先选择接触角的数值结果与理论结果符合情况验证模型[23],测试三个接触角:θω=60◦,90◦和120◦并将其与计算值θnum进行对比,θnum为平衡状态下的数值计算结果(平衡时液滴为圆弧,θnum由Rx,Ry求出).定义接触角达到平衡状态后的数值计算结果θnum与接触角θω的差和θω的比值为Eω=|θω− θnum|/θω,可用来衡量计算方法的准确性.表1展示了液滴在不同润湿性圆柱内表面达到平衡状态时给定接触角与数值计算结果的比较,可见两者误差较小.

为进一步验证模型,在本文的理论基础上创建与文献[24]参数相同的液滴撞击平面液膜模型,选取液滴直径d=2r为特征长度,计算域为H×L=4×6,运动黏性比rν=νL/νG=1,液-气密度比rρ=ρL/ρG=5,计算域左右侧边界为对称边界,上下侧为固壁边界,液膜厚度Hw=0.4.图3中给出了雷诺数Re=200,韦伯数We=5000时本文模拟结果与文献[24]的对比情况(这里撞击参数和时间的定义和文献[24]相同).可见本文模拟结果与文献结果符合度很高,从而验证了本文方法对液滴撞击问题研究的可信性.

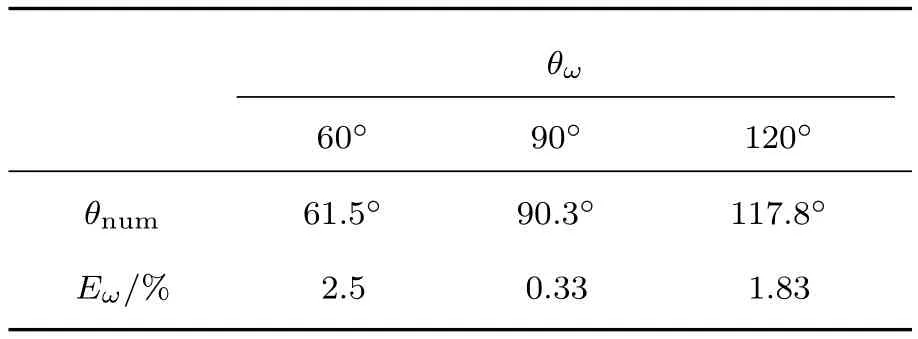
表1 液滴在不同润湿性的圆柱表面达到平衡状态时数值推断出的接触角和给定接触角的比较Table 1.Comparison of the contact angles of a droplet on the inner surface of a cylinder in equilibrium state deduced numerically and the specified ones.

本文研究液滴撞击圆柱内表面问题时,选择初始状态给定的液滴撞击速度UImp为特征速度,可得到基于UImp的撞击韦伯数、撞击雷诺数和撞击毛细数:LLrUImp/ηL,CaImp=ηLUImp/σ, 易知CaImp=UImp/Ur=WeImp/ReImp.为便于与其他文献中采用直径作为特征长度的结果进行对比,本文中WeImp,ReImp的值均是基于直径计算得到,后文中提到的We均指WeImp,Re均指ReImp.本文略有不同的是撞击参考时间是基于半径计算,即tImp=r/UImp,所有时间均以tImp为单位.

图2 (a)铺展系数Rx,Ry示意图;(b)不同网格密度下的铺展半径RxFig.2.(a)Schematic of spreading parameters Rx,Ry;(b)spreading radius Rxobtained by different grid density.

图3 Re=200,We=5000时本文模拟得到的一些时刻的界面(右侧蓝色图形)与文献[24]中结果(左侧红色图形)的比较Fig.3.Comparison of the interface shapes at selected times by the present simulation(right blue graph)and from Ref.[24](left red figure)at Re=200 and We=5000.

3.1 动力黏性比和密度比的影响

为研究密度比对液滴撞击行为的影响,本文数值模拟了计算域为140×280(Nx×Ny),液滴半径r=1,圆柱半径R=3,(xcd,ycd)=(0,1.5),(xcy,ycy)=(0,3.5),接触角θω=90◦,Re=200,We=5,20,50,动力黏性比rη=1,液体和气体的密度比rρ=1,5,20,50时(运动黏性比rν=1,0.2,0.05,0.02)液滴撞击圆柱内表面形态变化的过程.对于气-液两相流,两种流体的密度和黏性通常相差较大.本文考虑了密度比和动力黏性比较小的情形,一方面是为了研究这两个参数的影响,另一方面也可以为一些相对不常见的二元流体系统(如密度和黏性有可能近乎相等的水-硅油等)或者临界点附近的气-液系统提供有价值的信息.图4给出了铺展系数(Rx,Ry)在液滴沿圆柱内表面的铺展、收缩过程中随时间t的变化.

图4显示液滴撞击圆柱内表面时会先向下沉积,随后Ry达到最小值,Rx达到最大值,密度比越大振荡幅度越大,周期越短.这是由于密度比越大,气体的密度越小,气体惯性所起到的作用越小.这和二维表面张力波问题中密度比的影响很相像[25].We=5和20(We=50,rρ=50时计算不稳定,图中未给出),密度比分别为20和50时,Rx和Ry随时间变化差异很小,表明对于液滴撞击圆柱内表面的问题,密度比足够大时其对液滴形态变化影响较小.

图4 不同密度比下液滴在圆柱内表面沿x和y方向长度的变化(从上到下We数分别为5,20和50)Fig.4.Changes of the droplet lengths in the x and y direction on the inner surface of cylinder at different density ratios(The Weber number from upper to lower is 5,20 and 50).

图5 不同运动黏性比下液滴在圆柱内表面沿x方向和沿y方向的变化(从上到下We数分别为1,5和50)Fig.5.Changes in the x and y direction of the droplets on the inner surface of cylinder at different kinematic viscosity ratios(the Weber number from upper to lower is 1,5 and 50).

现就We=1,5,50,密度比不变(rρ=5)时运动黏性比(此时动力黏性比固定为运动黏性比的5倍)变化的液滴撞击圆柱内表面问题进行研究.图5显示:We较小(We=1)时,黏性比越大,液滴的最大铺展半径越大,且在圆柱内表面的振荡幅度更大.黏性比增大意味着气体的黏性变小,液滴受到的剪切阻力较小.从图5也可以看出,黏性比对振荡周期影响较小.结合图4可见,振荡周期在更大程度上受密度比影响.

此外,图5显示,We=1时,运动黏性比为20和50的情况下,铺展系数随时间的变化几乎一致,即小We数下,黏性比足够大时,其对液滴撞击圆柱内表面的影响较小.当We数增大到50时,液滴在收缩过程中沿对称线的变化(Ry)在高黏性比和低黏性比有所不同,出现非单调性变化,这可能是由于We较大时,撞击后从接触线前端引起的表面张力波更为剧烈,在高黏性比(气体黏性较小)时不易被阻抑,传播到液滴中部而引起Ry振荡.从图5可看出大We数下,黏性比变化对液滴变形结果的影响更显著.

总体而言,We数较小时,黏性比和密度比大到一定值以后,其对液滴撞击圆柱内表面现象的影响较小,对较大的We数,黏性比和密度比的增大对撞击现象产生的影响要更显著,但增大到一定值后其影响也在逐渐减小.一般情况下,密度比越大,最大铺展系数越大,液滴振荡幅度越大,周期越短;黏性比越大,振荡幅度越大,周期也略有增升.在碰撞初期,黏性比对液滴铺展几乎没影响,这可能由于碰撞初期剪切流动刚开始发展,黏性力只起相对次要的作用.

3.2 液滴初始速度的影响

本节研究液滴初始速度对撞击过程的影响.图6显示r=1,R=3,(xcd,ycd)=(0,1.5),(xcy,ycy)=(0,3.5),Re=200,θω=90◦,rρ=5,rν=1时,液滴在We=1,15,50,100沿圆柱内表面的铺展情况.表2为液滴以不同初速度(不同We数)撞击圆柱内表面时在圆柱内表面的铺展参数变化.

液滴在撞击圆柱内表面时会出现铺展收缩交替出现的过程,现将液滴铺展、收缩过程较为明显的时间t=1.2,2.8,4.4,6.0及液滴处于平衡状态(We不同达到平衡状态时间不同),液滴铺展情况在We数不同的情况下进行对比.

图6显示随We数增大,液滴撞击圆柱内表面后在圆柱内表面的铺展越明显.We=1时,液滴在圆柱内表面只发生铺展和收缩;We=50时,液滴在圆柱内表面铺展过程中边缘出现翘起;We=100时翘起更加明显,且翘起处颈部半径较小.当液滴速度增加时,液滴向下的动量越大,动能也越大,而撞击后液滴在圆柱内表面对其向上的作用力持续作用下失去向下的动量,转而沿圆柱内表面切向铺展,初速度越大,液滴受到的挤压越严重,沿切向铺展的速度也越大,铺展过程中液滴铺展前端接触线由于受黏性阻力和圆柱内表面的法向压力作用而减速,圆柱表面速度为零(接触线速度不为零但较小),初速度越大液滴铺展前端区域的剪切流动越剧烈,液滴前端动态接触角越大,气体越容易进入液滴铺展前端和圆柱内表面之间,使翘起更容易发生.液滴在撞击后达到的稳定状态一致,但小We数情况下液滴铺展收缩的振荡幅度较小.

表2 液滴初始撞击速度及相关参数Table 2.Initial impact velocity of droplet and other related parameters.

图6 不同We数下t=0.2,1.2,2.8,4.4,6.0和最终平衡状态(从左到右)时液滴的变形Fig.6.Deformation of the droplet at t=0.2,1.2,2.8,4.4,6.0 and the final equilibrium state(from left to right)at different Weber numbers.

当We数增加到400,600时(见图7)可以看到液滴翘起处颈部半径越来越小直至液滴发生分裂,即t=9.6(We=600),11.2(We=400)时的现象,We=600时液滴翘起部分在t=9.6和12.6会发生两次分裂,We=400时液滴只发生一次分裂.从前期(t=1.0,4.4)可以看出,液滴的翘起都和气体进入液滴铺展前端和圆柱表面之间相关,翘起部分由于惯性力和剪切力持续作用而被过分拉伸变形(呈细长形),表面张力在翘起尖端局部(较小区域)又逐渐重新占据主导作用,到某个临界点使液滴发生分裂,以降低表面能,分裂出的小液滴因尺度较小,之后又在表面张力作用下逐渐变为圆形(以使表面能最小).

图7 We=400(上)和600(下)液滴撞击圆柱内表面的变形情况Fig.7.Deformation of droplet impacting the inner surface of cylinder by We=400(upper)and 600(lower).

3.3 液滴初始位置对液滴撞击行为的影响

本节考虑初速度相同但初始高度h(液滴最低点与圆柱内表面最低点的距离)不同时,液滴撞击圆柱内表面的情况,探讨初始高度对液滴撞击行为的影响.对初始高度h=0,0.5,1.0和1.5的情况进行模拟,为了尽可能降低周围气体对撞击现象的影响,将密度比、动力黏性比均设置为38(密度比过大时计算易不稳定),圆柱半径R=3,We=50,Re=200.

首先对初始高度h=1.0的情况进行分析.图8给出了撞击的不同阶段中几个时刻界面的形态.密度比和动力黏性比较大时,液滴在最初的下降阶段受周围气体的影响较小,液滴形状和初始圆形相比偏差不大(见图8(a)t=1.0);当液滴进一步接近圆柱底部后与壁面间的气体排出较多,液滴和壁面间有较薄的气体层,且液滴首先在此气体层上铺展(如图8(a)t=1.2,1.3,1.35).对液滴及其周围(圆柱凹侧底部附近)气体进行分析,此阶段圆柱对流体的压力起主导作用,该压力有向上的分量,其持续作用使得流体向下的动量逐渐减小.

图9(a)给出了t=1.2时的压力分布图,可见此时液滴下方为高压区域;图9(b)给出了t=1.35时的压力分布图,可知随着时间推移,高压区域逐渐离开液滴中心向铺展方向移动,在液滴铺展前端出现低压区域,且前端因有较大的压力梯度而逐渐凸起.由图9推断,液滴在此阶段的铺展主要源于压力梯度的驱动,表面张力的作用相对次要.随着铺展过程的发展,由于前端凸起部分的Kelvin-Helmholtz不稳定性[26]导致气液界面在某时刻发生较大扰动,或由于圆柱内表面向上弯曲,液滴极小部分开始与圆柱内表面接触(如图8(a)t=1.35,1.4),接触后界面张力(包括气-液、气-固及液-固间的界面张力)也开始影响界面的局部运动.接触圆柱表面后的初始铺展阶段,前进接触线附近的流体速度较大,流体剪切力相对界面张力占优,动态(前进)接触角大于所给的静态(平衡)接触角(如图8(b)t=1.8,2.4),但随着前进接触线的推进,液滴被显著拉伸,液滴动能逐渐减小,一部分转化为表面能(液滴发生了显著偏离平衡状态的变形),另一部分被黏性耗散所消耗.随着前进接触线速度的减小,动态接触角又逐渐减小至静态接触角附近,此阶段某一时刻液滴铺展半径达到最大(如图8(b)t=6.8).由图8还可以看出,在液滴铺展前端接触到圆柱表面后,还有部分气体在液滴下方未完全排出而形成小气泡,气泡开始呈现非常扁平的状态(如图8(b)t=1.8),后在表面张力作用下,小气泡逐渐收缩,直至变成近乎圆弧形(图8(b)t=2.4,3.6).由于采用的相场模型特点[27]及网格解析度限制,气泡此后逐渐消失(可认为溶解于液滴中).铺展半径达到最大以后,液滴铺展前端开始回缩(图8(c)t=8.6),气液界面在表面张力作用下经历较大振荡后逐渐趋于平衡状态,即趋于圆弧形并处于圆柱底部(图8(c)t=40).

下面讨论铺展半径和各种能量的变化.图10给出了铺展半径、液滴动能、表面能及黏性耗散随时间的演化.对于二维问题,假设在第三维上为单位长度,从初始时刻到t时刻的黏性耗散:

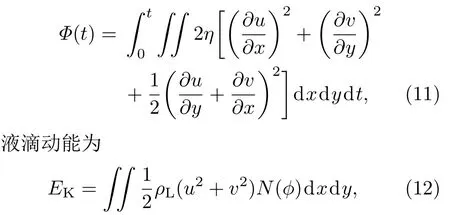
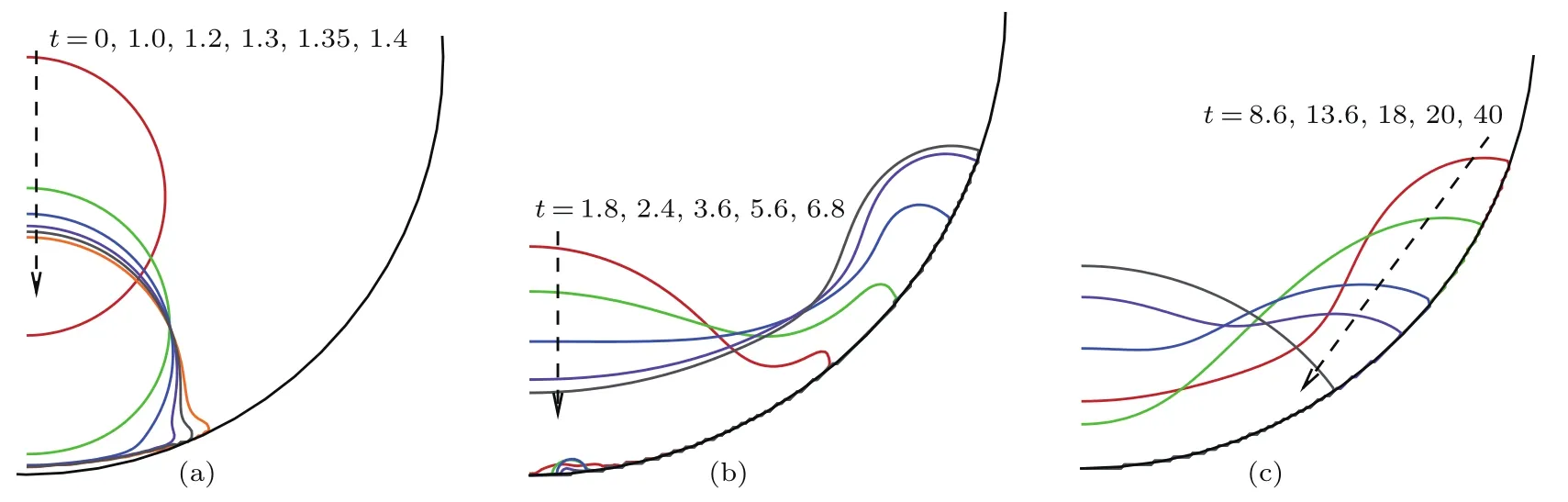
图8 h=1.0时液滴撞击圆柱内表面的三个阶段不同时刻的界面 (a)液滴下降至开始接触圆柱内表面;(b)液滴在圆柱内表面铺展至最大铺展半径;(c)液滴回缩至圆柱底部Fig.8.The three stages of droplet impact on the inner surface of a cylinder when the initial height is 1.0:(a)Droplet falls and starts to contact the inner surface of cylinder;(b)the droplet spreads on the inner surface of the cylinder and reaches the maximum spreading radius;(c)the droplet retracts to the bottom of the cylinder.

图9 初始高度h=1.0时,在(a)t=1.2和(b)t=1.35条件下液滴撞击圆柱内表面的压力分布、界面形状(白线)和流场(红色为高压区域,蓝色为低压区域)Fig.9.With an initial height of 1.0,the pressure distribution,interface shape(white line)and the flow field(red is high pressure area,blue is low pressure area)of the droplet impact on the inner surface of a cylinder at:(a)t=1.2;(b)t=1.35.

其中,N(ϕ)当ϕ>0时取值为1,否则为0.总表面能ES可结合(1)式进行计算得到.图10中的各种能量是与选取的参考能量相比的结果,图10(a)中液滴动能的坐标采用了对数尺度(因其变化尺度跨度较大).从图10(a)可见,在撞击的第一阶段,动能降低较缓慢,液滴形状和流场变化都还较小;在第二阶段,动能迅速降低,液滴铺展半径达到最大时,动能尚未降到局部最小(因动能采用对数尺度,此时动能也已很接近局部最低点),此后动能都维持在较小值(降到初始值的近1%),反映在液滴铺展达到最大后表面张力起相对主导作用.从图10(b)可见,表面能一开始变化很小,在第一阶段末、第二阶段初有显著增加,因这段时间液滴发生了较大变形,表面能显著增加的同时,黏性耗散也迅速上升,可看出这段时间流场内剪切流动也比较剧烈,随后黏性耗散变化相对平缓;进入第三阶段后,表面能快速减小,对应液滴分裂后回缩到平衡状态的过程,此阶段黏性耗散增加缓慢,流动较前期更为平缓.

当初始高度h发生变化时,液滴撞击过程与h=1.0的情况类似,均经历三个阶段(h=0时无初始下降阶段),且液滴最终都停滞于圆柱底部趋于平衡状态.不同高度对撞击过程的影响主要表现在液滴下方出现滞留的小气泡(h=0时没有发现明显的气泡),但一段时间之后气泡都溶解消失.图11给出了Rx和Ry随时间的演化,可见这两个量的变化在不同初始高度非常相似.以上结果表明,当密度比和动力黏性比较大时,初始高度对液滴撞击的结果影响较小.

图10 初始高度为1.0时液滴撞击圆柱内表面过程中各参量随时间的变化 (a)铺展半径及液滴动能;(b)表面能及黏性耗散Fig.10.With an initial height of 1.0,the evolutions of various quantities with time in the process of droplet impact on the inner surface of a cylinder:(a)Spreading radius and droplet kinetic energy;(b)surface energy and viscous dissipation.

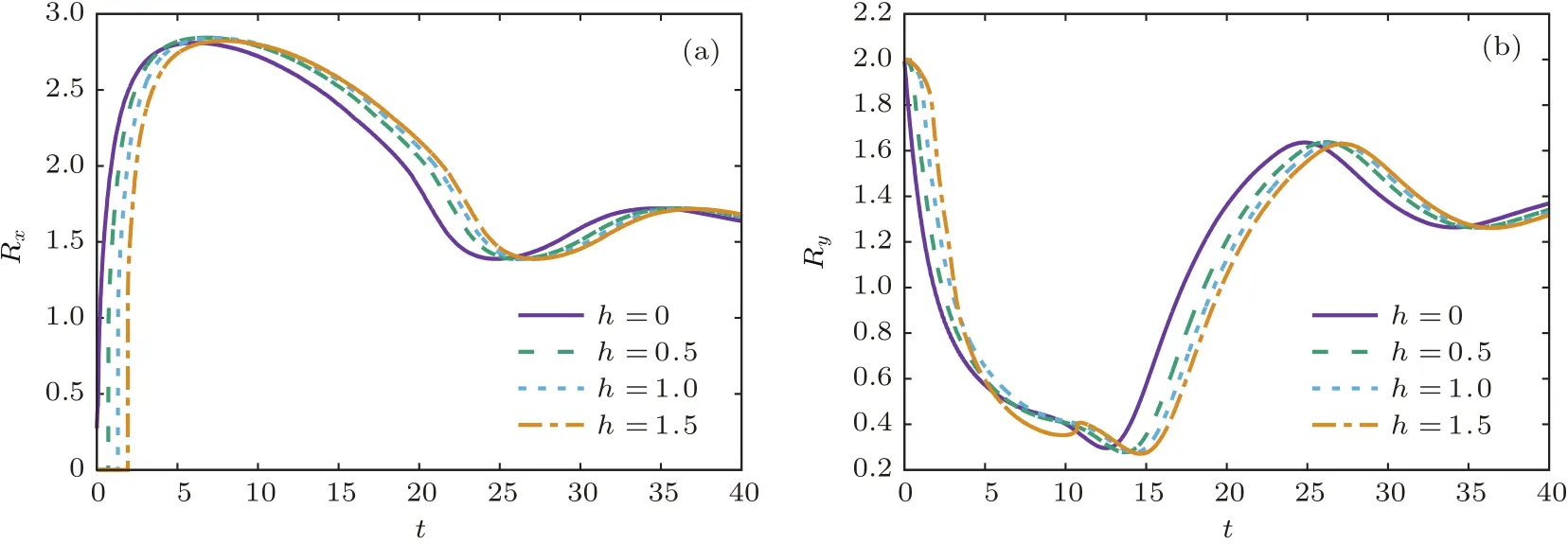
图11 不同初始高度下液滴撞击圆柱内表面过程中(a)Rx,(b)Ry随时间的演化Fig.11.Evolution of(a)Rx,(b)Rywith time at different initial heights of droplets impacting on the inner surface of a cylinder.

3.4 圆柱相对半径对液滴行为的影响

对于液滴撞击圆柱内表面问题,改变圆柱相对半径Rs(R/r)可研究凹曲面曲率半径变化时对液滴撞击行为的影响.当圆柱半径趋近于无穷大时,该问题可转变为液滴撞击平面问题.本节采用液滴半径r=1,初始高度h=1.0,密度比和动力黏性比为38,We=50,Re=200,θω=90◦,分析圆柱相对半径Rs=R=3,5,8,20和无穷大时的撞击现象,发现撞击过程和液滴形态变化总体趋势相同,液滴都经历了铺展、回缩、再铺展、再回缩,最终沉积在曲面上的过程.图12给出了圆柱相对半径Rs=8和Rs=∞两种情况下部分时刻的界面,与3.3节图8相比,可发现不同点主要在于最大铺展半径、达到最大铺展半径的时刻及撞击初始阶段滞留于液滴下方的小气泡.圆柱相对半径越大,液滴下方滞留的小气泡越小且消失的时刻越早.这是由于圆柱半径越大,液滴两侧和固体表面间距离越大,撞击过程中液滴下方气体越容易被从两侧排出.图13给出了上述五个圆柱相对半径下Rx和Ry随时间的演化(图13(a)中插图给出了最大铺展半径随圆柱曲率1/Rs的变化).从图13(a)可以发现,最大铺展半径随圆柱半径的增加而增加,但增加速度逐渐变小,最终趋于常数,即撞击平板时的最大铺展半径.这是由于圆柱半径较小时,液滴撞击后的最大铺展半径不仅受撞击We数等物理参数的影响,也很大程度上受由圆柱几何特性的影响.而当圆柱半径增加到一定程度再发生变化时,圆柱曲率变化不大,最大铺展半径主要受物理参数影响.由图13(b)可看出,圆柱相对半径越小,液滴撞击后的振荡幅度越小,振荡周期越短.这是由于在越小的圆柱内,液滴受到的几何限制越大.

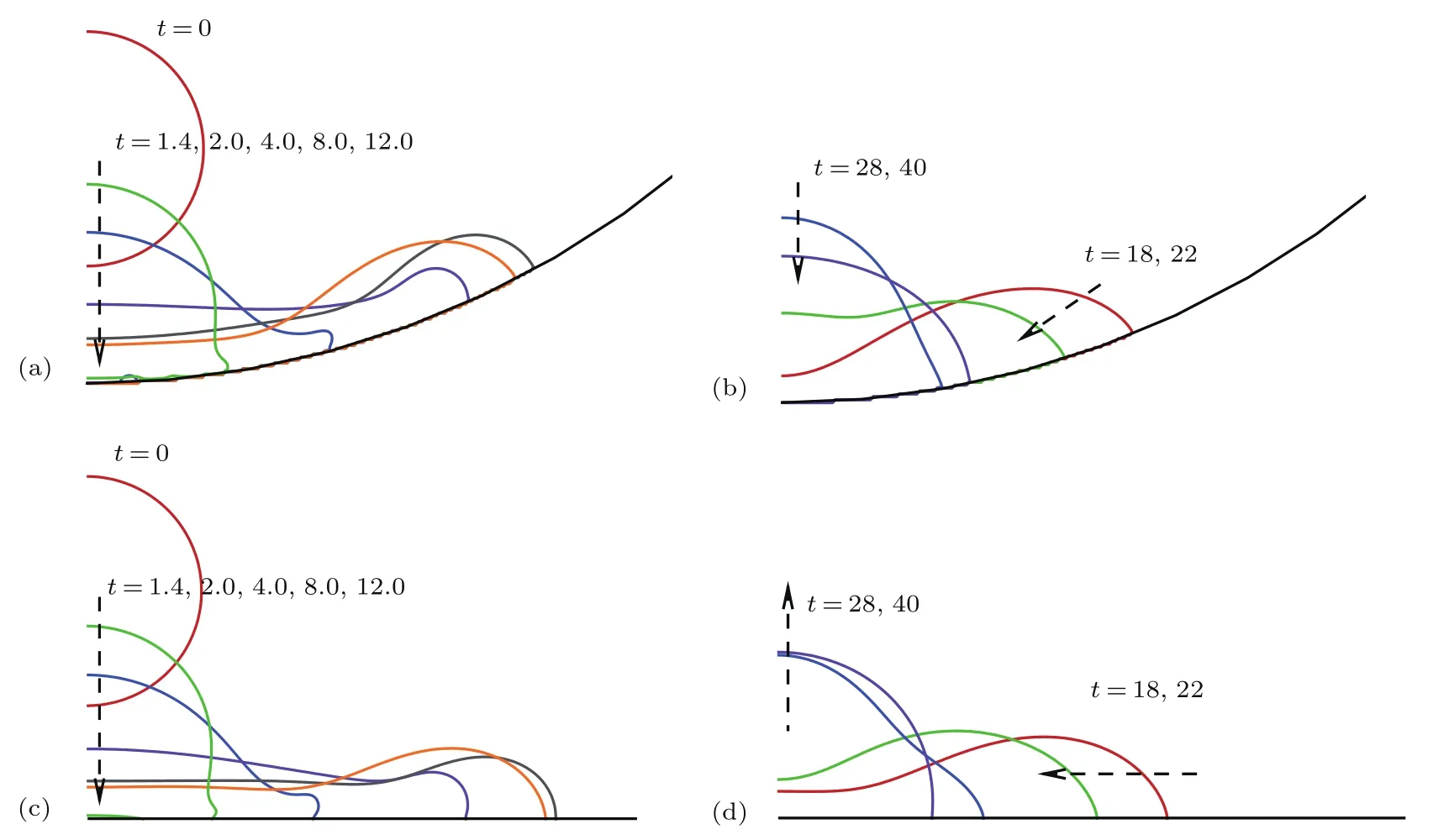
图12 在不同圆柱半径下一些时刻的界面形状 (a),(b)Rs=8;(c),(d)Rs=∞Fig.12.Interface shapes at some moments with the radius of cylinder being:(a)and(b)Rs=8;(c)and(d)Rs=∞.

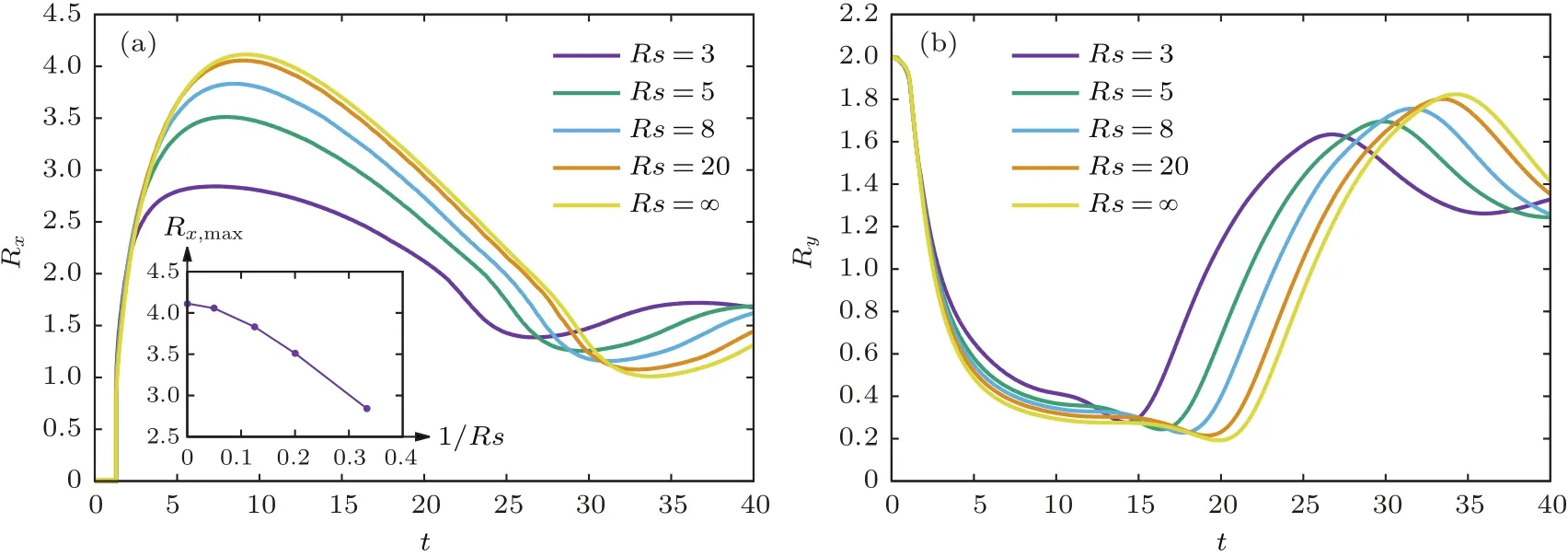
图13 不同圆柱相对半径下(a)Rx,(b)Ry随时间的演化Fig.13.Evolution of(a)Rx,(b)Rywith the time when the radius of cylinder is changed.

3.5 圆柱内表面润湿性对液滴撞击行为的影响

为研究圆柱内表面润湿性对液滴撞击动力学行为的影响,本文模拟了圆柱内表面接触角不同时,液滴撞击圆柱内表面的动态过程.计算域为3.5×7,半径R=3,Cn=0.1,Re=200,We=50,rρ=38,rν=1,圆柱内表面的接触角θω分别设置为60◦,95◦和150◦.图14给出了液滴撞击不同润湿性圆柱内表面过程中界面形态在几个时刻的变化.

由图14可见,圆柱内表面接触角越大,液滴在壁面的最大铺展半径越小.这是由于接触角越大,壁面的疏水性越大,对液滴的排斥力越大,液滴的铺展越容易受到抑制.当接触角增至150◦时,液滴回缩过程在圆柱内表面底部出现反弹现象.接触角较小时,液滴接触圆柱内表面后沿壁面快速铺展,液滴最大铺展半径更大,铺展过程更长,黏性耗散更大,更重要的是,对应较小接触角的接触线平衡位置距离圆柱底部更远,在回缩过程中,接触线到达该位置后液滴失去进一步回缩的动力,之后在此位置附近振荡而无法反弹.而接触角较大时,液滴沿壁面的铺展程度较低,铺展回缩过程中能量耗散较小,而且对应较大接触角的接触线平衡位置距离圆柱底部更近,回缩过程更长,这使液滴重新获得的动能更大,即使接触线到达该位置后,液滴具有足够大向上的动量仍然能进一步回缩直至反弹.

图14 圆柱表面接触角为60◦(红色实线)、95◦(蓝色点划线)和150◦(绿色虚线)时液滴的形态变化Fig.14.Morphological changes of a droplet impacting on the inner surface of a cylinder at θω =60◦ (red line),θω =90◦ (blue dash dot line)and θω =150◦ (green long dash line).

3.6 重力作用的影响

图15 初始高度h=1.0,不同Bo数下(a)Rx随时间的演化,(b)t=40的界面Fig.15.With an initial height of 1.0,(a)the evolutions of Rxwith time and(b)the interfaces at t=40 under different Bond numbers.

之前的模拟中没有考虑重力作用,可适应于微重力或者尺寸较小、表面张力较大的液滴.本节简要考虑Bo=0(包括Bo=0.2和1.0)的情况,并与Bo=0的结果进行比较.除Bo数不同,其他参数均相同:rρ=38,rν=1,Rs=3,h=1.0,θω=90◦.图15(a)所示为在这三个Bo数下Rx随时间的变化,可见在所考虑的Bo范围内,Bo的变化对于最大铺展半径影响较小,但在后续时间,Bo数越大,Rx的振荡幅度越小,周期越小,衰减越快.这表明重力的作用会抑制液滴撞击后在圆柱内表面的振荡,加快液滴达到平衡状态的过程.图15(b)给出了这三个Bo数下t=40的界面,此时液滴的振荡幅度已经较小,整体已接近平衡状态.由图15(b)可见,Bo越大,液滴形状越偏离圆弧状,而呈现较扁平的状态,这和日常现象的观察相符,即较大的液滴更易被自身重力“压扁”.

4 结 论

本文采用两相流相场LBM模拟研究了液滴撞击圆柱内表面的过程.结果表明:液滴撞击圆柱内表面过程中会出现铺展、收缩、反弹、液滴分裂、气泡滞留等现象;韦伯数变化对液滴最初的铺展程度变化影响较大,韦伯数足够大时液滴撞击会产生飞溅现象;密度比和动力黏性比增大到一定程度以后,再增加对结果影响相对较小;在密度比和动力黏性比较大时,液滴初始高度的变化会影响一些局部细节,如下方滞留的小气泡等,但对撞击过程总体特征影响较小;圆柱相对半径较小时,其变化对液滴的铺展程度影响较大,另外圆柱半径越大,滞留气泡越小;圆柱内表面接触角越大,液滴越易发生反弹;若考虑重力,则液滴的振荡会在一定程度受到抑制.本文只研究了二维问题,与实际情况还有一些差别,后续将使用三维模型做进一步研究.