具有非线性食饵收获的随机捕食-食饵模型

蓝桂杰，付盈洁，魏春金，张树文

(集美大学理学院，福建 厦门 361021)

0 引言

长期以来，捕食-食饵模型的动力学行为一直是生态学与生物数学的研究热点之一。在过去的几十年里，已经提出了许多捕食-食饵模型，并获得了许多丰富的研究成果[1-3]。文献[1]提出了以下模型

(1)

其中:x(t)，y(t)分别表示食饵和捕食者在t时刻的种群密度；模型的所有参数都是正的；r1，r2分别表示食饵和捕食者的内禀增长率；a1表示食饵种群的密度制约系数；b1是捕食者对食饵的捕获率；b2y/x表示具有Leslies形式的捕食者数量反应。文献[1]得到了模型(1)存在唯一的全局渐进稳定的正平衡态。文献[3]指出，在食饵x严重稀缺的情况下，捕食者有其他替代的食物来源，但由于食饵x不足，捕食者的增长仍将受到限制。所以将模型(1)的b2y/x修改为b2y/(k2+x)，其中k2为捕食者y的环境容纳量。

在经济和生物方面，食饵或捕食者或两者的收获又是另一个重要研究课题[4-16]。捕获强度对种群的动力学行为起到了非常重要的作用。因此，收获函数在描述捕食-食饵模型的动力学行为中起到了关键的作用。文献[4]指出，非线性收获比常数收获和比例收获更贴近实际。此外，在现实生态系统中，各种形式的环境干扰都是无时不在、无处不在的，生态系统中的各个种群都会受到不同形式和不同程度的环境干扰的影响。近年来，涌现出大量的文献致力于研究随机生物种群与随机传染病模型的动力学性质，并取得了丰富的研究成果[11-18]。本文假设只对食饵进行捕获，而捕食者没有经济价值，构建以下随机捕食-食饵系统:

(2)

1 预备知识

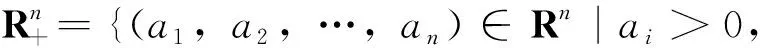
dX(t)=f(X(t)，t)dt+g(X(t)，t)dB(t)，t0≤t≤T。

(3)

定理2[19-20](It公式) 设X(t)(t≥0)是方程(3)的解。V∈C2，1(Rn×R+;R)，则V(X(t)，t)仍是It过程，具有随机微分dV(X(t)，t)=(Vt(X(t)，t)+VX(X(t)，t)f(t)+0.5trace[gT(t)VXX(X(t)，t)g(t)])dt+VX(X(t)，t)g(t)dB(t),a.s.,称此式为It公式。

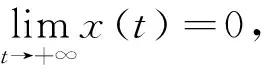
考虑下列随机微分方程

dX(t)=X(t)[r1-a1X(t)]dt+σX(t)dB(t)，

(4)

其中r1，a1，σ都是正常数，B(t)是标准的布朗运动。

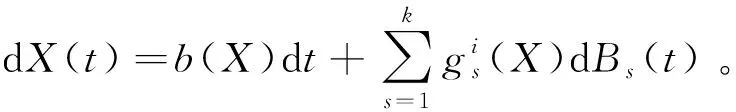
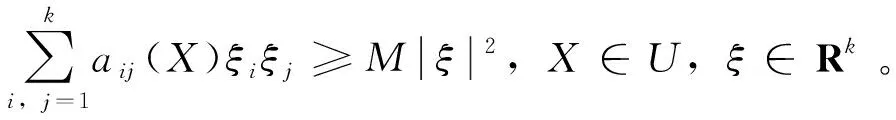
为了验证(A2)成立，只要证明存在非负的C2-函数及邻域U，使得对于任意的X∈ElU，LV(X)是负的。

2 主要结果

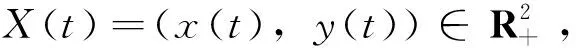
证明令u(t)=lnx(t)，v(t)=lny(t)。由It可得

(5)

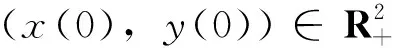
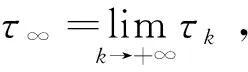
事实上,对于-a1x2-b2y2-a1x2y+(r1+r2)xy，若x≥(r1+r2)/a1，则上式小于等于零，即有上界。若x<(r1+r2)/a1，则-a1x2-b2y2-a1x2y+(r1+r2)xy≤-b2y2+((r1+r2)2/a1)y依然有上界。类似的可证存在常数N1∈R，使得

LV≤N1。

(6)

下面的证明与文献[21] 的相似，省略。

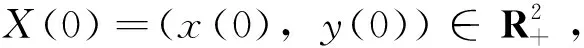
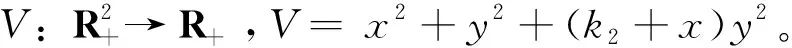
定义W=etV，对W应用It公式可得，LW=et(V+LV)≤et(x2+y2+(k2+x)y2-2a1x3-2b2y3-与不等式(6)的证明类似，存在N2>0使得LW≤N2et，即dW=et(LVdt+(2σ1x2+σ1xy2)dB1(t)+(2σ2(k2+x)y2+σ2y2)dB2(t)+Vdt),上式两端从0到t积分，并取均值可得E(W(t))≤W(0)+N2(et-1)，即E(x2+y2+(k2+x)y2)≤W(0)e-t+N2(1-e-t)<+∞。因此E2|X|≤E<+∞，最后应用Chebyshev不等式就能得到结论，所以省略。

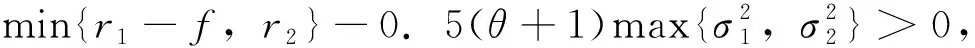
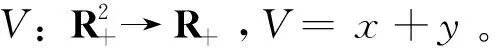
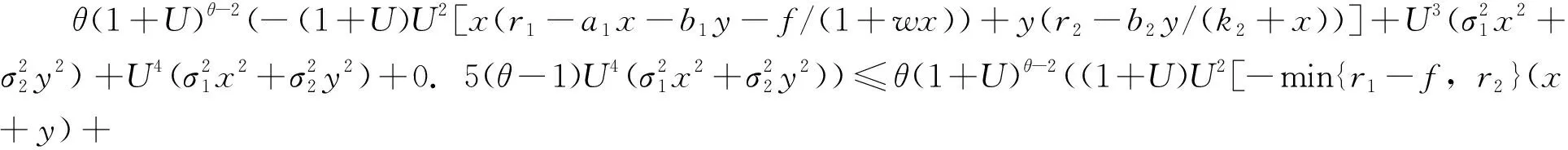
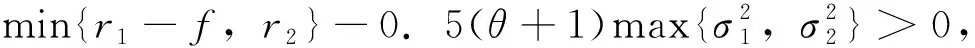
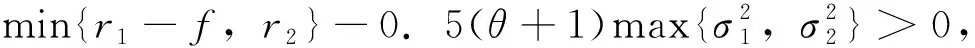
结合定理5、定理6及Chebyshev不等式，可以得到结论。

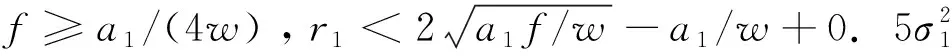
证明ⅰ)对lnx应用It公式可得,σ1dB1(t)。

ⅱ)对lny应用It公式可得，d lnσ2dB2(t),两边同时从0到t积分并除以t再取极限，由强大数定律可得,t-1ln即y(t)=0，a.s.。类似地，对于任意的ε>0，存在T0和Ωε，当t>t0和ω∈Ωε，都有P(Ωε)≥1-ε和b1y≤ε。所以有x(r1-a1x-f/(1+wx)-ε)dt+σ1xdB1(t)≤dx≤x(r1-a1x-f/(1+wx))dt+σ1xdB1(t)。

定理9 设系统(2)满足(r1-f)/b1>r2k2/b2，a1>fw,

b1M2/(2r2(a1-fw))]2，b2(y*)2}

(7)

证明首先考虑下面二元方程组

(8)

将上述方程组的第二个方程代入第一个方程可得ax2+bx+c=0，其中a=-(a1+b1r2/b2)w，b=-(a1+b1r2/b2+(r1-b1r2k2/b2)w)，c=r1-f-b1r2k2/b2。

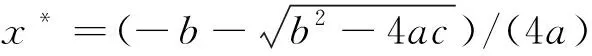
显然当(r1-f)/b1>r2k2/b2，方程(8)存在唯一的正解，不妨设为(x*，y*)。

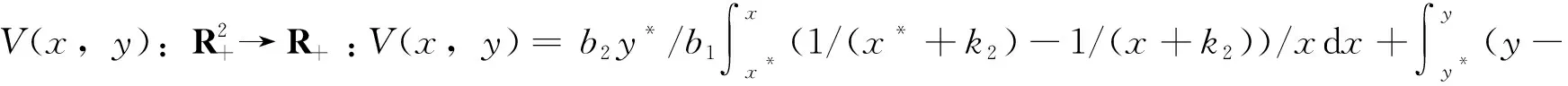
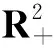
定理10 设系统(2)满足(r1-f)/b1>r2k2/b2，a1>fw，则系统(2)的确定系统存在唯一的全局渐近稳定的正平衡态。

3 数值模拟

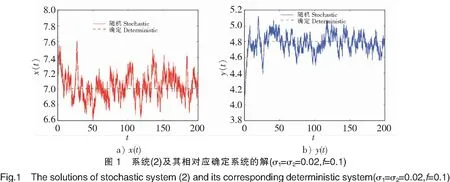
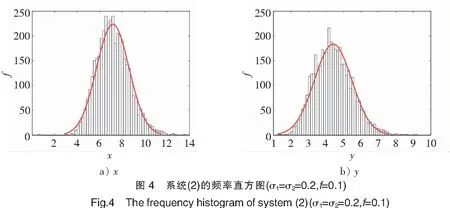
为了验证理论结果，采用Milstein高阶方法[24]对随机系统(2)进行数值模拟。取r1=1.2,r2=0.3，k2=1，b2=0.5，b1=0.1，w=0.6，a1=0.1和初值(7，4)，通过取不同的σ1，σ2，f来研究白噪声和收获对系统(2)的影响。

3)取σ1=1.8，σ2=0.2，f=0.1，显然满足定理8条件ⅰ)，即食饵灭绝，捕食者平均持续生存(见图5)。从图5可知食饵x灭绝，捕食者y平均持续生存。

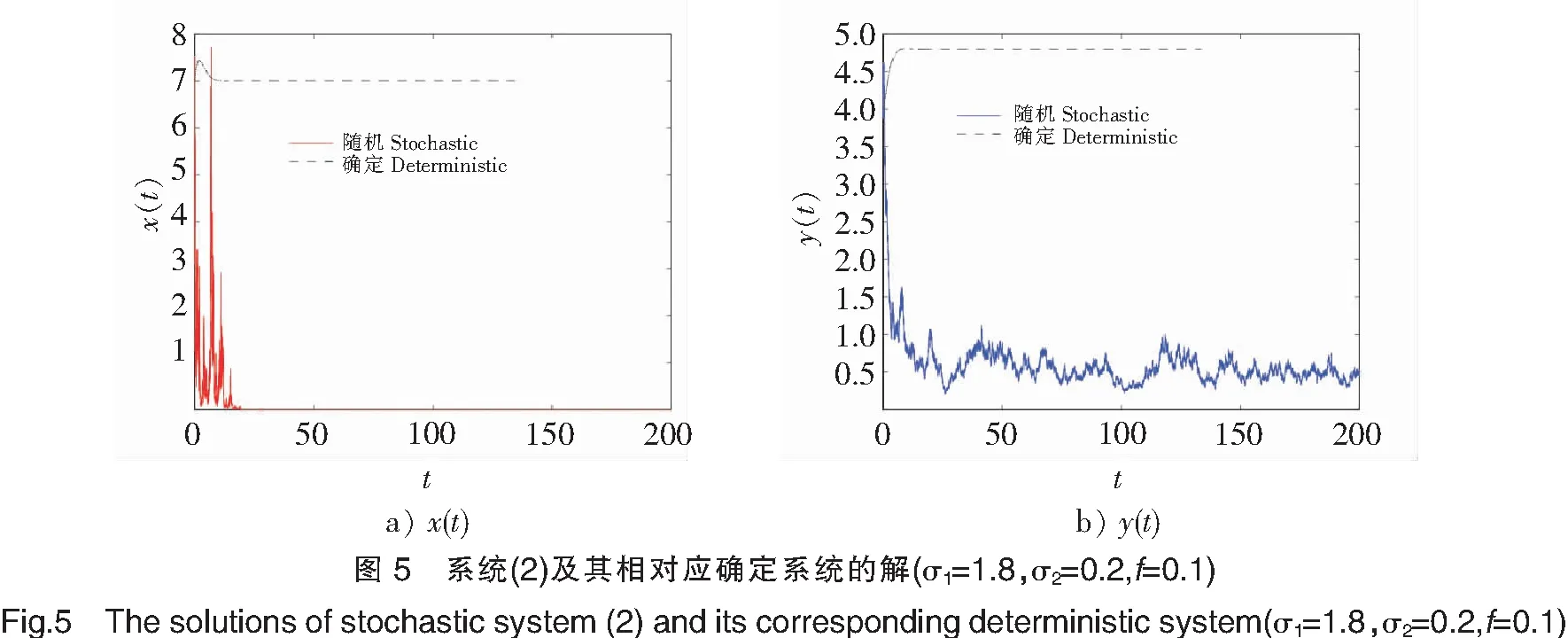
4)取σ1=0.2，σ2=0.8，f=0.1，显然满足定理8条件ⅱ)，即捕食者灭绝，食饵平均持续生存(见图6)。从图6可知食饵x灭绝，捕食者y平均持续生存。

5)取σ1=1.8，σ2=0.8，f=0.1，显然满足定理8条件ⅲ)，即食饵和捕食者均灭绝(见图7)。从图7可知食饵x灭绝，捕食者y平均持续生存。

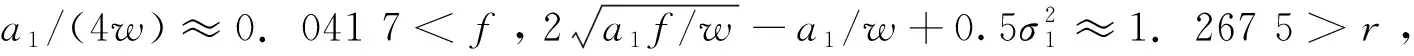
数值模拟结果显示，白噪声强度的大小和人类的捕捞活动都对物种的生存起着至关重要的作用，即过大的干扰会使物种灭绝，过度的捕获食饵，食饵也将灭绝。