基于激光传感器定位的非完整AGV导引控制
杨素珍
(漳州职业技术学院机械工程学院,福建 漳州 363000)
0 引言
自动导向车(automatic guided vehicle,AGV)是现代化物流的重要设备,主要用于各种环境下的物料储运,因其具有安全、灵活、高效等优点,日益得到广泛应用。AGV是移动机器人的一个重要应用分支,导引控制AGV以一定的精度沿着特定轨迹运行是AGV进行预规划路径导航的基础。为了实现有效的导引控制,首先得解决AGV的定位方法和控制方法的问题。激光传感器定位[1]是利用3个及以上激光反射板的位置信息,实现AGV的自定位。与磁点定位[2]、RFID定位[3]、视觉定位[4]等方法相比,激光传感器定位更为灵活,抗干扰能力强,且定位精度高,方便进行路径规划和自由路径导引,成为目前AGV系统较为普遍应用的定位方法之一。导引控制方法可采用轨迹跟踪[5]和路径跟随[6],相比之下,路径跟随不要求参考轨迹随时间变化,其前进速度可自由设定,从而方便行程统计,更适用于AGV系统的集中调度规划。非完整AGV是一个复杂的多输入多输出非线性系统,由于受到非完整约束,运动空间受限,其路径跟随控制器设计难度较大。本文将对非完整AGV的数学模型、激光定位方法、路径跟随控制器算法进行研究,并给出仿真实验情况。
1 AGV运动学模型分析

研究对象(2,0)型[7]非完整AGV的结构如图1所示,它由车体、两个独立驱动轮和万向轮组成,其中:xoy为全局惯性坐标系{U};xcocyc为局部坐标系{F};θ为AGV的导向角度;Oc为AGV的质心;de为Oc与Op之间的距离;θr为路径曲线Op点的切线与x轴的夹角;v和w分别为AGV的线速度和角速度;两驱动轮间的距离为2b;轮子半径为r。
万向轮用来提高AGV的载质量能力,通过控制两驱动轮的不同转速可实现AGV各种运动形式。


(1)
式中:S为WMR的广义Jacobian 矩阵;u=[vw]T为速度输入矢量,各矩阵取为

定义坐标系{U}到坐标系{F}的旋转矩阵为:
(2)
又因为
(3)

(4)
式中:ϑ为路径起始点到Op点的轨迹长度,Op与O重合时ϑ=0;有界且可微的c(ϑ)为路径Op点的曲率。则在Serret-Frenet 框架下有如下关系成立:
“弗”在《齐》中未见,“弗”与“不”的使用在殷周时期大体是1∶2,此后“弗”的数量大幅下降,看两部文献“弗”与“不”使用相差悬殊,仅《周》见一例,此例中“弗”加及物动词没有带宾语,虽然表强调的功能扩展,仍无法与“不”竞争[6] 。可见《周》的用法比《齐》略丰富,南方比北方语法更发达。
(5)
其中:
而
(6)
定义AGV新的坐标状态集合为(ϑ,de,θe),结合式(1)、式(5)和式(6)可得AGV的路径跟随运动学模型为[8]:
(7)
式中:θe=θ-θr。式(7)表明非完整AGV系统为一个变量耦合的多输入多输出非线性系统。
2 AGV激光传感器定位方法
AGV使用的激光传感器通常也称为激光测距仪,其工作原理是测量发射光束与从物体表面漫反射光束的时间差,并结合激光的传播速度,计算出其与反射物体之间的距离。为了获得更好的反射效果,提高测量精度,反射物体通常采用专用的激光反射板。该反射板安装于AGV所处空间的已知位置,在AGV初始位置已知后,激光传感器内部的激光头进行周期性的固定角度旋转扫描,从而可获得3个或以上反射板的位置和角度信息,再应用三角测量法和统计方法获得自身的定位信息。和其他定位方法相比,该方法具有不易受环境影响,测量速度快,定位精度高的特点。
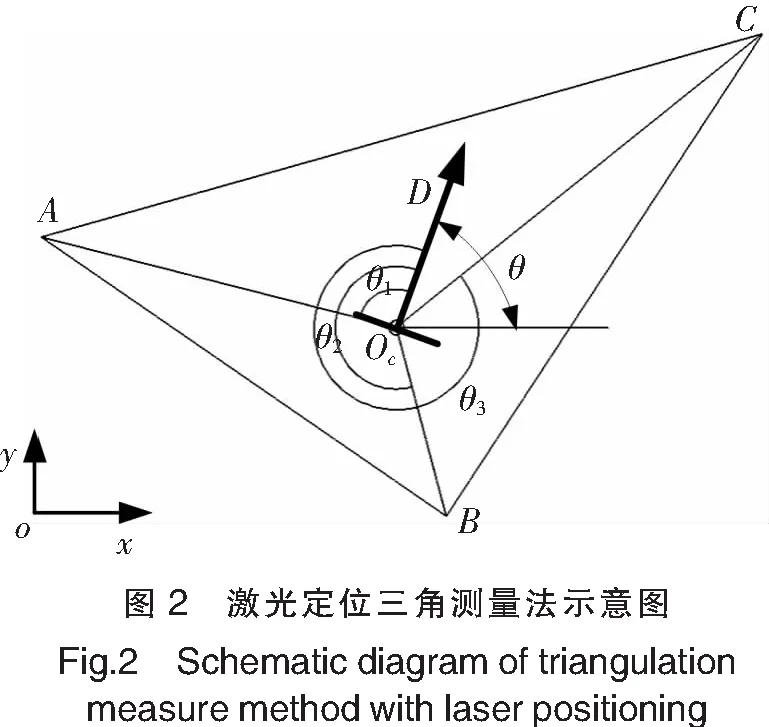
以仅3个反射板的激光定位三角测量法为例,其定位原理如图2所示。图中,A(x1,y1),B(x2,y2)和C(x3,y3)为3个激光反射板的已知安装位置,∠AOcD=θ1,∠DOcB=θ2,∠DOcC=θ3为当前时刻激光传感器扫描检测获得的反射板与AGV前进方向的夹角(顺时针为正值),则有如下方程成立:
(8)
(9)
式中:AGV初始位置在直线上方时del取正,反之取负值;θl为直线的倾斜角度。
对于圆轨迹(xc-c1)2+(yc-c2)2=R2,AGV路径跟随误差值dec和θec分别为
(10)
3 激光导引控制器设计
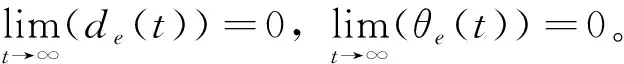
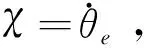
(11)
式中,k2为正的常数。对式(11)求导,并将式(7)代入可得
(12)
设计控制律为
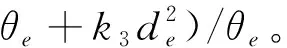
(13)
式中,k1和k3为正的常数。将式(13)代入式(12)可得
(14)
假设
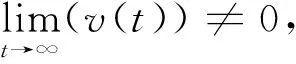
(15)
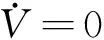
(16)
可以保证系统是渐近稳定的。
4 仿真实验分析
为了验证本文方法的有效性,在Matlab环境下进行仿真实验。仿真时间为10 s;采样周期为0.01 s;AGV结构参数取:r=0.04 m,b=0.2 m;路径跟随控制器取:k1=10,k2=6,k3=1;AGV的初始速度v=1.414 m/s,w=0 rad/s;直线轨迹参数为:a=1,b=-2,c=0;AGV的初始位姿分别取为:(1 m,2.1m,2 π/5),(1 m,0.5 m,π/3)。路径跟随情况如图3~图5所示,可见本文控制器可保证多个位姿下AGV的稳定导引控制。

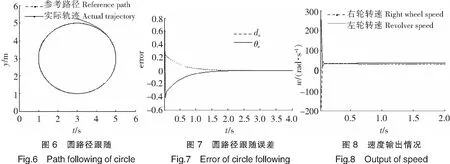
圆弧路径跟随实验,圆弧轨迹参数为:c1=3,c2=3,R=2;AGV的初始位姿取为:(3 m,5.2 m,π/4)。实验结果如图6、图7所示,系统距离误差到达稳态的时间为1.89 s,角度误差到达稳态的时间为2.08 s。达到稳态后,距离稳态误差均值绝对值为1.9044×10-4m,角度稳态误差均值绝对值为3.986×10-5rad,可见本文设计的控制器有较好地控制效果。圆弧跟踪的两轮速度输出如图8所示,速度没有大跳变,可见采用路径跟随的方式进行AGV导引控制有利于系统的平稳运行。
5 结 论
本文从定位方法和控制器设计两个方面研究了非完整AGV的路径导引控制问题,建立了包含AGV参考点与参考路径之间距离误差和角度误差的路径跟随误差控制模型,分析激光传感器多点反馈定位原理,并给出直线和圆弧路径的误差计算模型。借助Lyapunov理论,获得渐进稳定且结构简单的路径跟随控制器。仿真试验表明,该控制器能够快速消除路径跟随误差,且误差值较小,下一步将进行实际AGV 系统研究。

