识别特殊图形“破题”，重视经典问题教学——2018年“北、上、广”中考卷几何综合题导向分析

☉江苏省泰州市姜堰区实验初级中学 邱晓敏

许小燕老师在文［1］中从2018年北京中考卷第27题（一道几何综合题）说起，提出一些平面几何命题建议（特别是回归教材、坚守课标、重视经典几何问题）给笔者很多体会，引发共鸣，并由此思考了全国各地中考试卷对平面几何难题的考查呈现出明显的地区特点，比如一些平面几何难题多出现在一些地级市中考试卷中，像北京、上海、广州这些“超一线城市”却把命题重心都放在经典几何题、常见图形为背景的习题，这是值得我们关注和思考的.

一、2018年“北、上、广”平面几何综合题概述

考题1：（2018年北京卷，第27题）如图1，在正方形ABCD中，E是边AB上一动点（不与点A、B重合），连接DE，点A关于直线DE的对称点为F，连接EF并延长交BC于点G，连接DG，过点E作EH⊥DE交DG的延长线于点H，连接BH.

（1）求证：GF=GC；

（2）用等式表示线段BH与AE的数量关系，并证明.

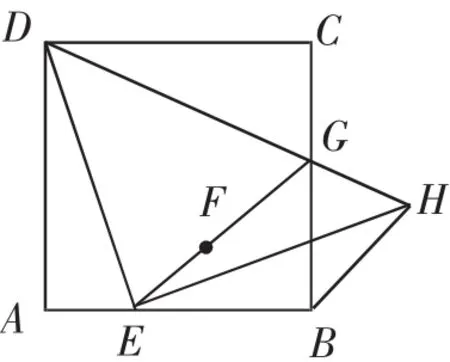
图1

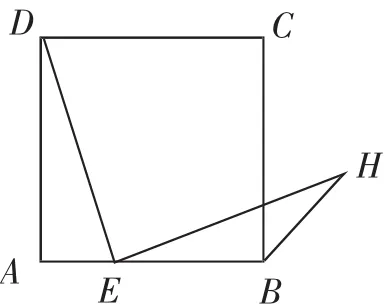
图2

思路概述：第（1）问是基础题，只要构造并利用全等三角形即可实现问题解决，第（2）问在前一问的基础上成果扩大后可得△DEH是等腰直角三角形.这样问题就转化为“教材习题”：如图2，正方形ABCD中，点E为AB边上任意一点，连接DE，将线段ED绕点E顺时针旋转90度到HE，连接HE，可证出BH平分正方形一个外角（或∠CBH=45°），也可证出BH=AE.

考题2：（2018年上海卷，第25题）已知⊙O的直径AB=2，弦AC与弦BD交于点E，且OD⊥AC，垂足为点F.

（1）如图3，如果AC=BD，求弦AC的长；

（2）如图4，如果E为弦BD的中点，求∠ABD的余切值；

（3）连接BC、CD、DA，如果BC是⊙O的内接正n边形的一边，CD是⊙O的内接正（n+4）边形的一边，求△ACD的面积.

图3

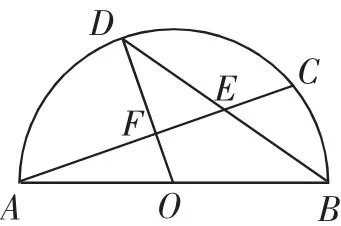
图4

思路概述：第（1）问强化条件“AC=BD”后，可得出特殊三角形（如△ABC是含30°角的直角三角形，△AOD是等边三角形等）.第（2）问随着“E为弦BD的中点”的强化，如图5，连接OE、BC，由垂径定理，得△ODE是直角三角形，EF⊥OD，于是可导出一组相等的角：∠ODE=∠AEO=∠ABE=∠DBC，于是可证出△AEO △ABE，有AE2=AO·AB=1×2，于是AE=，待求∠ABD的余切值恰是△ABE与△AEO的相似比

图5

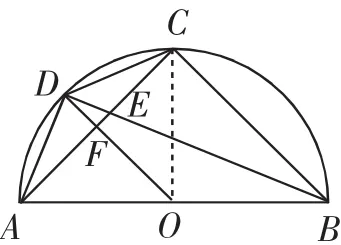
图6

解第（3）问的关键是由正多边形的条件信息，沟通弦AD、CD、BC所对圆心角度数（用含n的式子表示），如°，这样由∠COB+∠COD+∠AOD=180°，得出关于n的方程180，解得n=4.于是调整图形为图6，∠AOD=∠COD=45°，∠BOC=90°，问题转化与等腰直角三角形相关的计算问题，容易求出

考题3：（2018年广州卷，第25题）如图7，在四边形ABCD中，∠B=60°，∠D=30°，AB=BC.

图7

（1）连接BD，探究AD、BD、CD三者之间的数量关系，并说明理由；

（2）若AB=1，点E在四边形ABCD内部运动，且满足AE2=BE2+CE2，求点E运动路径的长度.

图8

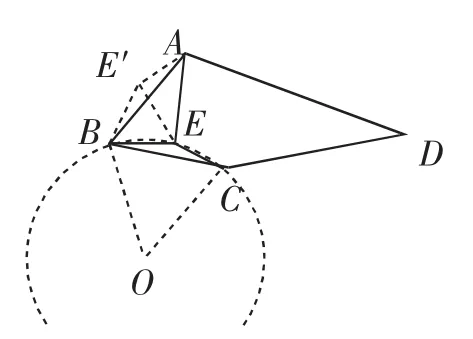
图9

思路概述：（1）如图8，将△BCD绕点B逆时针旋转60°，得△BAD′，连接DD′.先分析出等边三角形BDD′，再证∠BAD+∠C=270°，得出∠DAD′=90°. 由勾股定理，得AD2+AD′2=DD′2.代换得AD2+CD2=BD2.

（2）如图9，将△BEC绕点B逆时针旋转60°,得△BE′A，连接EE′.先证等边三角形BEE′.结合AE2=BE2+CE2，代换出AE2=EE′2+AE′2，可得∠AE′E=90°，∠BE′A=150°，∠BEC=150°.问题转化为“BC弦确定，圆周角∠BEC=150°”（对于这类问题，有资料上总结为所谓“定弦定角”问题）.从圆的角度想到点E在以BC为弦，优弧（所对的圆心角为300°的圆上.以BC为边在下方作等边△BCO，则O为圆心，半径BO=1.所以点E的运动路径为

二、“北、上、广”平面几何命题的导向之思

平面几何难题是一些地区中考试卷用来承担区分功能的把关题，在限时考试的环境下，有些平面几何难题“杀伤力”很大，少数优生投入不少时间却极容易“隐性失分”.最近几年，笔者也大量收集各地较难的中考平面几何综合题进行训练，但从个人的练习体会来看，有些地级市的平面几何题确实繁难，其难点常常表现在以下几个方面.一是图形线条太多（如哈尔滨市中考卷），一看如此之多的线条，学生往往望而却步，放弃思考；二是图形虽然线段不多，但涉及旋转，且增加了动点参与之后的旋转，需要构造旋转前者对应的图形，构图很难；三是图形虽然看似经典，但另出新的设问，且破解方法相对单一，虽然最后只要添加一条辅助线就能解决，或取一个中点即可攻克，但是考生往往会有很多无效念头的干扰，影响思路的获取.诸如此类，既是笔者个人解题的体会，也是教学过程中大量观察学生面对平面几何难题的一些现状.然而，我们看到“北、上、广”三地关注的却是教材上的经典问题，这样的命题对教学和命题有怎样的导向呢？以下提出笔者的一些思考.

1.关注教材例、习题，教学时可通过变式探究使得成果扩大

由于所谓学案导学的盛行，当前教学中对教材关注度不够不是少数现象，因为导学案“沦落”为习题拼凑式的练习案是一个较为普遍的现象（见文［3］），特别是在规模较大的学校，集体备课往往就是选题填充到习题导学案上，课堂上基本没有时间关注课本，新概念、新定理的教学常常是“一个定义，三项注意”式的讲解，而教材上的很多例、习题也往往被忽略，直至在一些教辅资料或各级考试中再被考到，又会成为练习讲评的重点.我们认为，对教材上的例、习题要认真教学，不止于满足教材的要求，还要在跟进的习题教学时，继续对教材例、习题进行变式教学，让学生在变式探究过程中加深对教材例、习题的理解，达到做一题、会一类、通一片的教学效果.

2.重视经典问题，命题时可将经典问题适当包装后考查

平面几何教学主要是训练学生的推理证明能力，并在此过程中熏陶“步步有据”的理性精神，懂得凡事应该有“客从何处来”的治学追求.但是探究繁难的几何性质、辅助线添加却不是义务教育课程标准所要求的，那只是少数参加数学竞赛学生的挑战要求.所以作为平时教学与命题，对经典问题充分关注十分有必要，像上文中“北、上、广”三地考查的都是经典问题（在有些老师眼中都是一些陈题、旧题），这难道不是一种命题上的引领吗？难道是这些经济、文化处于领先地位的超一线城市命题专家们不懂创新，反而回归经典吗？回复上述疑问，也许那句“因为懂得，所以慈悲”可为之一辩.

3.对于几何奇异性质，平时教学可引导学生探究但不宜考查

我们知道，平面几何中有很多美妙、奇异的性质，如三角形的三条角平分线（中线、高线）交于一点、圆中很多奇异的线段乘积的性质（比如托勒密定理等），然而这些性质被课标或教材删减不学，其背后的原因值得细思，如圆中很简单的“相交弦性质”被删减，对相似三角形的判定定理的要求也只是了解，而且不得利用相似进一步探究相关命题，等等.这些在课标文本中都有明确的要求，不知什么原因很多地级市中考试题中对国家层面的教学要求视而不见，不但对圆的考查要求太高，而且对利用相似三角形探究更为奇妙的性质保持着个性化的兴趣，作为平时教学引导学生深入探究，让优秀学生挑战难题、享受几何的美妙，是值得肯定的，然而这种兴趣并不一定适合全体学生，更不宜放在高利害的中考试卷中.想起近一段时间，各级教育行政主管部门严查所谓校外机构“超标、超纲、超前”教学，然而引发这些不良现象的深层次原因何在呢？是否也应该检讨一下各地区中考命题的“现实引领”呢？