从一道中考题看概率问题事件分析的重要性

一、问题提出

在阳光体育活动时间，小亮、小莹、小芳和大刚到学校乒乓球室打乒乓球，当时只有一个空球桌，他们只能选两人打第一场.如果确定大刚做裁判，用“手心”“手背”的方法决定其余三人哪两人打第一场.游戏规则是：三人同时伸“手心”“手背”中的一种手势，如果恰好有两人伸出的手势相同，那么这两人上场，否则重新开始.这三人伸出“手心”或“手背”都是随机的，请用画树状图的方法求小莹和小芳打第一场的概率.(2015年山东省聊城市中考数学试题第22题）

参考答案：画树状图，如图1所示.

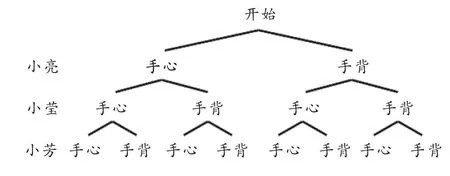
图1

所有等可能的情况有8种，其中小莹和小芳伸“手心”或“手背”恰好相同的情况有2种，则小莹与小芳打第一场的概率为

二、解题困惑

笔者所在学校的教师对该问题的理解持三种观点，分别是：

观点1：从小亮、小莹、小芳三人中选出两人打第一场，共有三种结果，分别为（小亮，小莹）、（小亮，小芳）、（小莹，小芳），并且是等可能事件，因此图1所示的树状图中第1、8两个分枝无法确定谁打第一场，理应舍去，即实际共有6种可能结果，所以正确答案为小莹与小芳打第一场的概率为

观点2：由于三人出现相同手势是客观存在的，且每种手势出现的机会是均等的，树状图中第1、8两个分枝是必要的、不可或缺的，因此参考答案正确.

观点3：基于对“否则重新开始”的文本解读，因此游戏的次数无法确定，若游戏要连续进行n次才能确定打第一场的选手，故小莹与小芳打第一场的概率为

三种观点，到底谁是谁非？老师们困惑不已.

三、惑因分析

笔者经过仔细思索，认为一线教师之所以存在困惑，其原因在于：

（1）在本题所提及的游戏中，是否为等可能事件呢？从概率类型来看，是否属于古典概型？这些是存在困惑的原因之一.

从游戏过程来看，每个人所出手势“手心”“手背”是随机的，而且可能性也是均等的，因此是等可能事件概率.小亮、小莹、小芳所出手势所有可能的结果如图1所示.其中小亮与小莹、小亮与小芳、小芳与小莹打第一场的概率均为，而无法确定小芳与小莹打第一场的概率同样为.因此从概率问题类型上看，这种游戏属于古典概型.

很显然，观点1不成立.

（2）解读题目提供的相关信息，发现实验次数无法确定（未确定谁打第一场时需继续实验直至确定出来为止）.但从题目中提供的参考答案看，命题者的本意是只需一次实验就可以确定小莹与小芳打第一场的概率.难道这个游戏实验一次与连续两次乃至连续三次……计算出的概率都是？这又是老师们困惑的另一原因.

为了进一步探索问题的根源，笔者请山东的许永忠老师利用EXCEL（软件版本为2010版）进行了游戏的随机模拟实验，结果如表1所示：

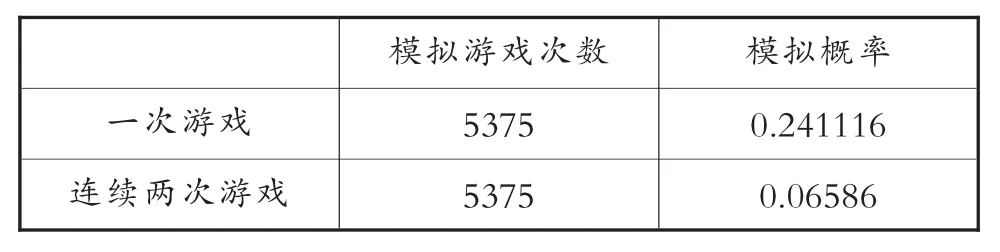
表1

从表中数据不难得出，观点2也不正确，只有观点3成立.

四、我来解惑

基于以上分析，运用古典概型可以得出如下结论：

1.经历连续不同次数的游戏，求出的概率是不相同的

（2）若一次游戏不能确定谁打第一场，则需要进行第二次游戏（即连续两次游戏），其计算要用到参考文献［1］中提及的等枝法，将图1的树状图再画一级，即在第1枝和第8枝下各生8枝，另外6枝下也分别生等“份量”的同结果的8枝，最后共有64枝，如图2所示.

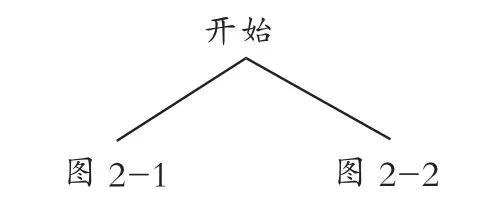
图2

其中，图2-1、2-2具体如下：

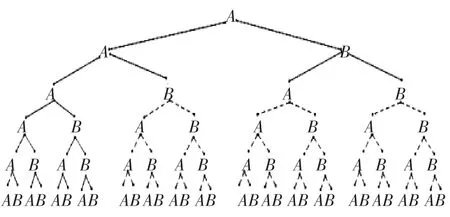
图2-1

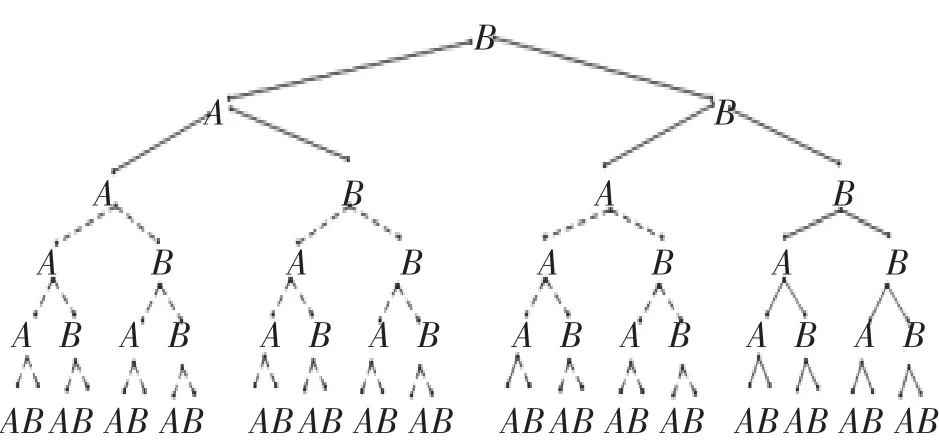
图2-2

说明：A——手心；B——手背；图中虚线所示树状图表示实际游戏中不需要进行，这里画出，是为了将这一游戏由非古典概型转化古典概型，便于相关事件概率的计算.

从图2可以看出，此时三人出现相同手势的分枝共有4枝，因此它的概率变成了，即通过连续两次游戏确定小芳与小莹打第一场的概率为.

以此类推，若连续两次游戏还不能确定谁打第一场，则要进行第三次游戏（即连续三次游戏），根据游戏的规则，这4种情形又要重新开始，即对应的这4枝下又生8枝，另60枝下也分别生等“份量”的同结果的8枝，共512枝，其中三人出现相同手势的分枝共有8枝，因此通过连续三次游戏确定小芳与小莹打第一场的概率为……显然，这个树状图若无限画下去，按照“等枝法”不难发现，连续进行n次游戏所得小芳与小莹打第一场的概率为）n.因此，笔者认为老师们所持的观点3是正确的.

2.该游戏不可能无限进行下去

在“连续进行n次游戏才能确定出三人中哪两人打第一场”的条件下，可以计算出小芳与小莹打第一场的概率为，即当n→+∞时因此连续游戏的次数不会很大.

基于“当n≥2时，小芳与小莹打第一场的概率计算难度很大，超出了课标要求”，因此建议将原题问题修改为“请用画树状图的方法求通过一次游戏确定小莹和小芳打第一场的概率.”