例谈中考数学几类规律探索型问题*

☉内江师范学院数学与信息科学学院 潘 超

☉内江师范学院数学与信息科学学院 程婧怡

规律探索型问题是中考数学中常考常新的典型试题.它是在一定条件下，探索发现有关数学对象所具有的规律性或不变性的问题，它往往给出了一组变化了的数、式子、图形或条件，要求学生通过阅读、观察、分析、猜想来探索规律［1］.解决这种问题的过程中，能渗透方程思想、函数思想、数形结合思想、数学模型思想、分类讨论思想、特殊与一般思想等.其中的一些数学思想，能体现“探究”的解题思维品质，具有趣味性、思想性、变化性、挑战性等特征，也能较好地体现“注重让学生在实际背景中理解基本的数量关系和变化规律”［2］等课标要求.因此，研究中考数学规律探索型问题对教学具有重要的现实意义.下面，结合近几年的中考题谈谈几类规律探索型问题.

一、“数式排列”型规律探索题

“数式排列”型规律探索题通常依据给定的一列数、式子或者等式，写出其中包含的一般规律.对这类问题的基本解法是，先写出基本结构，然后通过对比各组中的相同部分和不同部分，找出各部分的特点，最后得出一般性的结论［3］.这类问题通常包含数字排列型和式子排列型两种类型.

1.数字排列型

数字排列型规律探索题是指数字或代表数字的字母按照一定规律依次排列出现，需要探索蕴含在其中的某个指定位置的数值或关系的问题.

例1（2018年，十堰市）如图1所示，是按一定规律排成的三角形数阵，按图中数阵的排列规律，第9行从左至右第5个数是（ ）.

图1

评注：我们在解这类数字排列型规律探索题时，可以对出现的有限项的特征或规律进行猜测，再计算几组数据验证猜想，并以此解决问题.

2.式子排列型

式子排列型规律探索题是指按照一定规律给出有限组式子，并由此按要求归纳出一般性结论的问题.这类题中，各式往往与式子对应的序号存在一定的关联，通过计算和整理不同项，可以归纳得到与序号有关联的一般结论.

例2 （2018年，安徽省）观察以下等式：

图2

按照以上规律，解决下列问题：

（1）写出第6个等式：____________；

（2）写出你猜想的第n个等式：_____________（用含n的等式表示），并证明.

分析：以序号n为前提，依此观察每个数，可以发现规律.

评注：式子排列型规律探索题是通过归纳、猜想、构造等步骤解决复杂的问题.先发现有些项中共同的特征，再以此发现数字和序号的关系猜测第n项，解题方法与数字排列型规律探索题类似.

二、“图形变换”型规律探索题

“图形变换”型规律探索题即探索图形的变化规律，主要特征是“计数”，并着重讨论图形构成要素的变化规律.

例3（2018年，自贡市）观察图3中所示的一系列图形，它们是按一定规律排列的，依照此规律，第2018个图形共有_______个○.

图3

分析：每个图形的最下面一排都是1，另外三面随着图形的增加，每面的个数也增加，据此可得出规律，求得答案.

解：观察图形可知：

第1个图形：1+1×3；

第2个图形：1+2×3；

第3个图形：1+3×3.

……

第n个图形：1+3n.

所以，第2018个图形：1+3×2018=6055.

评注：“图形变换”型规律探索题重在培养学生的直觉思维和空间想象能力，通过运用数形结合思想对复杂图形进行简化和可视化，找到“形”与“数”之间的联系，归纳概括图形变化的规律.

三、“新型定义”型规律探索题

新型定义是指在题目中给出一个新概念或新方法，并对该概念或方法进行说明，要求学生能运用新的定义，解决题目中的规定问题，现学现用.

例4（2012年，扬州市）大于1的正整数m的三次幂可“分裂”成若干连续奇数的和，如23=3+5，33=7+9+11，43=13+15+17+19，…，若m3分裂后，其中有一个奇数是2013，则m的值是（ ）.

A.43 B.44 C.45 D.46

解析：分析规律，找出2013所在的奇数的范围可得解.由于23=3+5，33=7+9+11，43=13+15+17+19，…，则m3分裂后的第一个数是m（m-1）+1，共有m个奇数.因为45×（45-1）+1=1981，46×（46-1）+1=2071，所以2013是底数为45的数的立方分裂后的一个奇数，所以m=45.故选C.

评注：这是一道“新型定义”型规律探索题，主要考查学生的阅读理解能力，应用有理数知识分析和解决问题的能力.此题通过定义正整数m的三次幂的“分裂”，将其转化为一个不等式，采用“两边夹”得到m的值.［4］

四、“坐标变化”型规律探索题

“坐标变化”型规律探索题是指在直角坐标系中根据图形变化或性质探索点发生变化的规律的问题.

例5（2018年，安顺市）正方形A1B1C1O、A2B2C2C1、A3B3C3C2、…按如图4所示的方式放置，点A1、A2、A3、…和点C1、C2、C3、…分别在直线y=x+1和x轴上，则点Bn的坐标为______.

图4

分析：根据一次函数图像上点的坐标特征可得出点A1的坐标，结合正方形的性质可得出点B1的坐标，同理可得出点B2、B3、B4、…的坐标，再根据点的坐标的变化即可找出点Bn的坐标.（点Bn的坐标为（2n-1，2n-1），解答过程略）

评注：这种坐标变化规律探索问题，体现了“数”与“形”的结合.要解决这类问题，学生应具有良好的识图能力和符号意识，能将图形规律和数值变化规律结合起来.对于点的坐标的变化规律题，往往从特殊到一般，求解前几个点的坐标之后，不难发现它们之间存在着循环关系或递推关系，再综合运用图形的性质解决问题.

五、“实验操作”型规律探索题

“实验操作”型规律探索题是指将一个物品或图形通过折叠、剪拼、堆放、拆合、透视等动态模拟变换方式，得到新的物品或图形，再研究其几何性质或数量关系的试题.对这种问题，学生通过模拟操作，对同一对象，一层一层地计算，发现其中的规律.

例6（2015年，宁波市）如图5，将△ABC沿着过AB的中点D的直线折叠，使点A落在BC边上的A1处，称为第1次操作，折痕DE到BC的距离记为h1；还原纸片后，再将△ADE沿着过AD的中点D1的直线折叠，使点A落在DE边上的A2处，称为第2次操作，折痕D1E1到BC的距离记为h2；按上述方法不断操作下去，经过第2015次操作后得到的折痕D2014E2014到BC的距离记为h2015，若h1=，则h的值为（ ）.2015

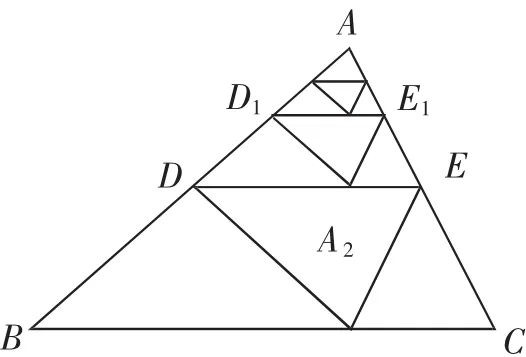
图5

解：DE是△ABC的中位线，D1E1是△ADE的中位线，D2E2是△AD1E1的中位线……

评注：学生一般对自己动手操作的东西感兴趣，一方面，不是枯燥地学习、接受知识；另一方面，通过自己一层层操作动手计算、发现规律、解决问题，获得成功的喜悦［5］.此类题有助于学生数学逻辑思维和创造思维的培养［6］.

以上仅仅介绍了部分规律探索型问题.事实上，这类中考试题在每年的中考试题中还会出现很多，这些试题都能不同程度体现以创新意识为立意，体现创新教育和素质教育的价值取向.在平时数学教学中，应注意激发学生强烈的创造欲望、勇敢的探索精神、深刻的体验意识、敏锐的观察能力、良性的思维品质，以及培养学生善于发现问题、提出问题、分析问题并创造性地解决问题的能力.［7］