基于改进MC算法的图像三维重建研究与实现

田应贵，程鹏

（1.四川大学计算机学院，成都 610065；2.四川大学空天科学与工程学院，成都 610065）

0 引言

近年来，计算机技术飞速发展，随着交叉学科的兴起，三维重建技术被广泛应用到各个行业中，特别是在医疗行业。三维重建算法可分为体绘制和面绘制两个大类，体绘制愈加真实地反映物体构造，然而运算量大，导致实时性较差，而面绘制则比体绘制运算速度快，实时性相对较强[1]，所以在实践应用中，目前图像三维重建的主流方法仍旧是面绘制。

Marching Cubes（MC）算法[2]是面绘制算法中的经典算法，它是W.Lorensen等人于1987年提出来的一种体素级重建方法[3]；MC算法因原理好理解并且算法易实现而得到了广泛的应用，但是算法在拓扑一致性、绘制精度以及重建速度上仍有许多需要改进和完善的地方。

本文以保持好的视觉效果同时提高重建实时性为出发点，展示了一种改进的MC算法，最终在Visual Studio 2015（v140）环境下，使用OpenGL可编程管线基于GPU绘制出重建后的三维图像，有效地实现了等值面快速提取，提高了医学图像可视化效果以及三维重建的效率。

1 移动立方体算法

移动立方体算法（下称MC算法）是在三维数据场中生成等值面的经典算法，它使用体素立方体抽取等值面，一般处理三维正交数据场[4]，表示：

定义1：

设 f(x,y,z)为三维连续图像，频域上占有限带宽，覆盖空间区域V，空间取样函数S(x,y,z)是理想的δ脉冲阵列[5]：

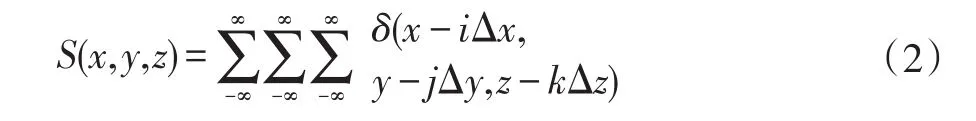
其中：

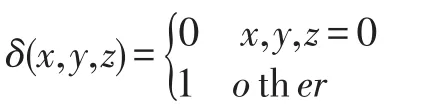
得到图像：

表示为三维立体数据。

1.1 等值面剖分模型

MC算法以体元作为基本处理单元处理正交场中的数据[6]，体元是由上下两张切片中8个相邻像素点构成的立方体，如图1。

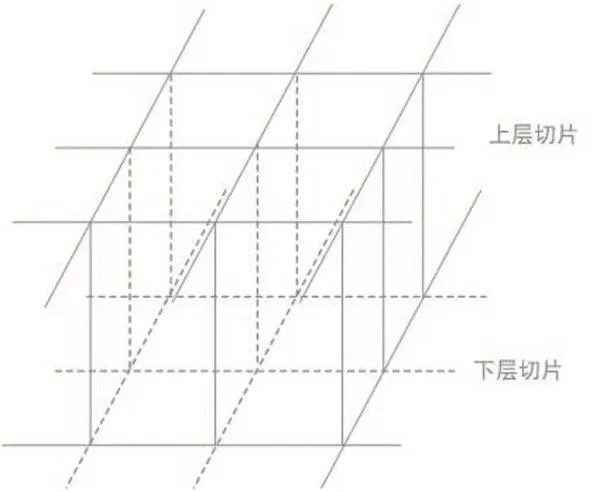
图1 体元模型

在使用MC算法处理体元数据过程中，一般从左到右，从上到下，从前到后依次处理每个体元，从而通过判定体元中各个顶点是在等值面外还是在等值面内对体元的8个顶点进行分类，根据顶点位置分布即可确定当前立方体等值面所对应的三角剖分状态。因为体元的8个顶点各有两个状态，由此我们可以得到256种索引状态，再由立方体对称性、旋转性、共轭性可将这256种剖分状态简化为15种，如图2。

图2 15种简化剖分模型

图中实心标记的顶点即为处于等值面内的点，有了这15种三角剖分模型便可建立一个包含256个索引项的三角剖分构型查找表，使用它来记录所有等值面的连接方式。此时根据编号进行线性插值运算[7-9]便可得到等值面的顶点坐标，公式如下：

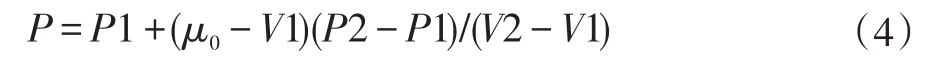
其中等值点坐标为P，边上两个端点的坐标分别为P1、P2，灰度值分别为V1、V2，给定的阈值为 u0。

1.2 等值面法向量的计算

在三维重建的可视化过程中，得到体元基本数据后，还要保证正确的链接各个等值点以形成等值面，由于每个点在等值面内沿面切线方向上的梯度分量为0，所以此时该点的梯度矢量方向就是要求的法向量[10]。但是等值面通常是两种不同密度物质的分解面，所以导致处于等值面上的点的梯度矢量不为0，传统MC算法使用线性插值计算法向量[11]：

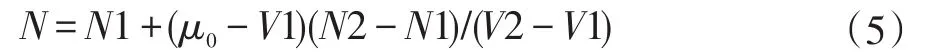
其中，等值点法向量坐标为N，边上两个端点的法向量坐标分别为 N1、N2，灰度值为 V1、V2，u0代表阈值。

2 中点法简化计算

三维重建中使用线性插值来计算等值点和法向量显得太过复杂，对于体元之间共有的棱边还会进行重复计算，一条棱边重复计算了4次，这增加了重建的时间代价和复杂性，因此本文使用中点法[12]简化计算，使用棱边中点代替线性插值点，三角面顶点坐标和法向量坐标表示如下：

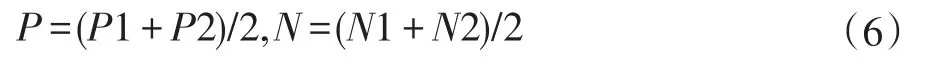
其中顶点坐标为 P，顶点法向量为 N，P1、P2，V1、V2分别为棱边的两个角点坐标和法向量。

3 OpenGL可编程管线

使用MC算法进行三维重建过程中会产生大量的三角片面，若是使用传统的固定OpenGL渲染管线，这将会增加CPU的负担，占用大量的时间空间片，大大降低了三维重建的效率，因此本文采用最新的OpenGL可编程管线进行三维重建，通过顶点着色器传递顶点数据，片段着色器处理法向量和颜色值进行可视化三维重建。

3.1 顶点处理

在使用MC算法进行三维重建过程中，会产生大量的三角片面，其中包括大量的顶点数据需要处理，如果每次得到一个三角片或者一个顶点数据就从CPU发送顶点数据到显卡，CPU会进行大量的重复工作，同时消耗大量的时间，因此本文提出使用顶点缓冲对象（Vertex Buffer Objects，VBO）[13]来管理内存分配，它会将大量的顶点数据存储在GPU中，我们可以一次性将大量的顶点数据发送到显卡，此时顶点着色器几乎能做到立即访问接受到的顶点数据，这个过程是非常快的。顶点缓冲对象的定义代码如下：

unsigned int VBO;

glGenBuffers（1,&VBO）;

//绑定独一无二的ID

glBindBuffer（GL_ARRAY_BUFFER,VBO）;

//绑定缓冲类型

glBufferData（GL_ARRAY_BUFFER,sizeof（vertices）,GL_STATIC_DRAW）;

//将顶点数据复制到缓冲内存中

3.2 顶点数据解析

在OpenGL可编程管线中，只要是以顶点属性的形式进行输入的数据，我们都可以将其传递给顶点着色器，这就要求在配置顶点时要具有很强的灵活性，因此我们要手动配置输入数据与顶点着色器顶点属性的对应关系，以保证在渲染前告诉OpenGL该如何处理接收到的顶点数据，OpenGL中顶点数据解析如图3所示：

图3 顶点数据解析

解析后位置数据以32位（4字节）浮点值的形式存储，每个位置有三个这样的数据，其中第一个值处于缓冲的起始位置，得到这些信息后OpenGL使用glVertex⁃AttribPointer函数配置顶点数据的解析方式：

glVertexAttribPointer（0,3,GL_FLOAT,GL_FALSE,3*sizeof（float）,（void*）0）;

glEnableVertexAttribArray（0）;

3.3 着色器状态配置

当我们绘制多个物体时，就需要重复的进行数据的绑定和链接以保证绑定正确的缓冲对象，从而重建过程中配置正确的顶点属性就显得极为麻烦，因此本文提出使用顶点数组对象（Vertex Array Objects，VAO）来把这些状态存储到一个对象中去，在每次需要配置顶点属性指针时，只需要将那些调用执行一次，之后在绘制物体时将其绑定到相应的VAO即可，顶点数组对象会存储glEnableVertexAttribArray和glDisableVertex⁃AttribArray的调用，通过glEnableVertexAttribArray配置顶点属性，通过glVertexAttribPointer调用相关联的顶点缓冲对象。

图4 顶点数组对象（VAO）绑定VBO

创建好VAO后，类似的可以使用glBindVertexAr⁃ray绑定VAO，再对属性指针和对应的VBO进行绑定，完成之后解绑VAO以供使用，此后每次绘制物体时，将VAO绑定到特定的设定上即可，代码如下：

//1.绑定顶点VAO

glBindVertexArray（VAO）;

//2.把顶点数组复制缓冲中

glBindBuffer（GL_ARRAY_BUFFER,VBO）;

glBufferData（GL_ARRAY_BUFFER,sizeof（vertices）,ver⁃tices,GL_STATIC_DRAW）;

//3.设定顶点属性指针

glVertexAttribPointer（0,3,GL_FLOAT,GL_FALSE,3*sizeof（float）,（void*）0）;glEnableVertexAttribArray（0）;

//..::绘制代码（渲染循环中）::..

//4.绘制代码

glUseProgram（shaderProgram）;

glBindVertexArray（VAO）;

glDrawArrays（GL_TRIANGLES,0,3）;

4 实验与分析

采用传统MC算法与改进的MC算法基于OpenGL可编程管线对医学CT扫描数据进行三维重建，实验环境为AMD A8-4500M 1.90GHz，4GB内存，64位Windows 10操作系统，数据为200×160×160的人脑CT数据，实验结果如图5所示。表1、表2为实验结果对比。

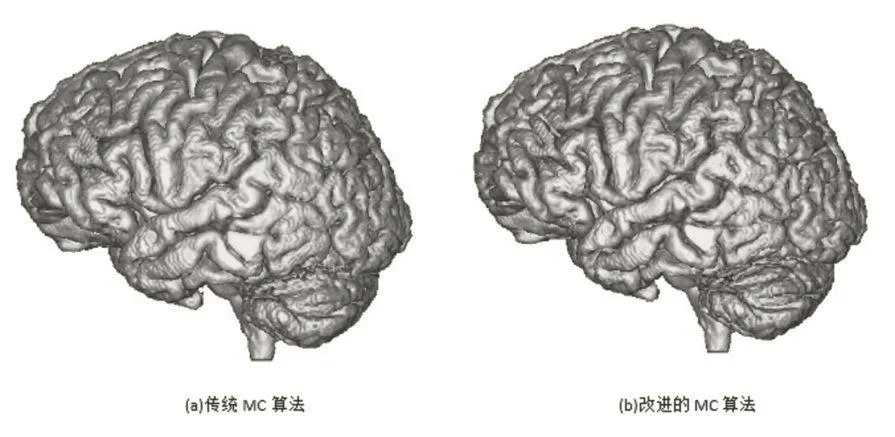
图5 大脑表面重建实验结果

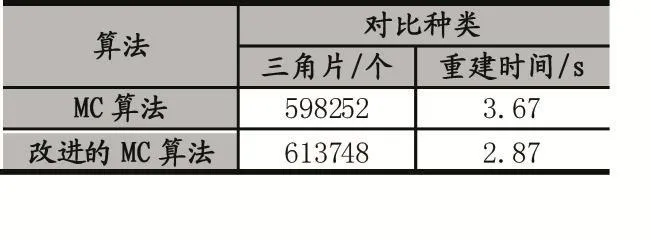
表1 OpenGL可编程管线下的实验对比

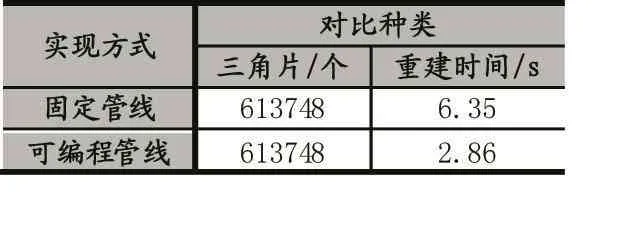
表2 改进MC算法在固定管线和可编程管线下的实验对比

实验对比结果可见，本文改进的算法相较于传统MC算法在生成的三角片数量上略有增加，重建图像质量上有一定提升，同时在使用了中点法改进算法之后，重建时间提升了21.8%；由表2实验对比可以看出，在医学图像重建中，使用MC算法会产生大量三角片和顶点坐标数据，本文使用OpenGL可编程管线中的顶点缓冲对象和顶点数组对象处理三角片和顶点数据，重建时间提升了55.1%，综上本文提出的改进方法在提升了重建图像效果的同时，运行时间取得了明显的改进。

5 结语

针对MC算法进行三维重建耗时过长、重建效果不佳等问题，本文使用OpenGL可编程管线结合改进的MC算法，使用中点法代替线性插值、顶点缓冲对象和顶点数组对象处理大量的三角片顶点数据，经过实验表面该方法在提升图像重建效果的同时，在算法耗时上得到大大提升，增强了MC算法的实时性，为算法在临床医学领域的应用做出了一定的贡献。