例谈中考“圆”的问题
肖 健
圆是初中平面几何中的重要内容,也是中考的重点内容.下面我们就一起来看下这部分内容常见的考点.
考点一:圆有关概念
主要考查圆及其有关概念,如弦、弧、圆心角、等圆、等弧的概念.
例1(2016·山东潍坊)木杆AB斜靠在墙壁上,当木杆的上端A沿墙壁竖直下滑时,木杆的底端B也随之沿着射线OM方向滑动.下列图中用虚线画出木杆中点P随之下落的路线,其中正确的是( ).
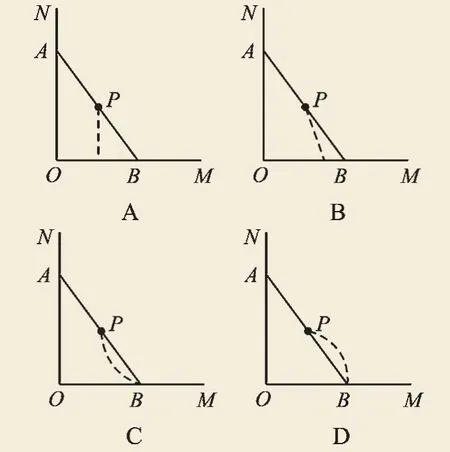
【解析】连接OP,显然OP是Rt△AOB斜边上的中线,由直角三角形斜边上的中线等于斜边的一半,可得OP=AB.由于木杆不管如何滑动,长度都不变,所以OP长为定值,所以P点就在以O为圆心的圆弧上.故选:D.
【点评】此题很灵活地考查了圆的定义:平面上到定点的距离等于定长的点的集合叫圆.木杆AB在运动过程中,位置是变化的,但其中P点到O点的距离保持不变.
考点二:圆的有关性质
主要考查圆的中心对称性、旋转不变性和轴对称性、垂径定理的使用.
例2(2017·青海西宁)如图1,AB是⊙O的直径,弦 CD 交 AB 于点 P,AP=2,BP=6,∠APC=30°,则CD的长为( ).

图1
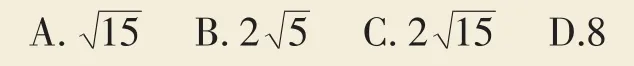
【解析】如图2,连接OC,作OH⊥CD于H.

图2

在Rt△OHC中,∵OC=4,OH=1,

【点评】结合条件,首先应该想到垂径定理,作出垂线段是解决本题的关键.圆中求半径长、弦长或弦心距,通常要综合使用垂径定
∴HC=HD,∵AP=2,BP=6,
∴AB=8,∴OA=4,∴OP=OA-AP=2,
在Rt△OPH中,
∵∠OPH=∠APC=30°,理、勾股定理、三角函数等知识.
考点三:圆周角概念、圆周角定理(推论)、圆的内接四边形性质定理
例3(2017·湖北荆州)如图3,A,B,C是⊙O上的三点,且四边形OABC是菱形.若点D是圆上异于A,B,C的另一点,则∠ADC的度数是

图3
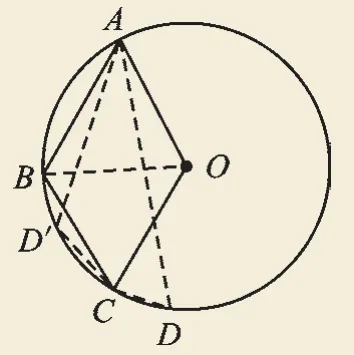
图4
【解析】如图4,连接OB,
易知AB=OA=OB=BC,
∴△AOB是等边三角形,
∴∠AOC=120°,
∴∠ADC=60°,∠AD′C=120°.
故答案为60°或120°.
【点评】此题考查了圆周角定理和圆的内接四边形的性质定理.由于D点位置不确定,所以要进行分类讨论.分类讨论思想的渗透是本题的亮点.
考点四:直线与圆的位置关系
主要考查直线是圆的切线的判定条件、直线与圆相切的性质.
例4(2017·浙江衢州)如图5,在直角坐标系中,⊙A的圆心A的坐标为(-1,0),半径为1,点P为直线y=x+3上的动点.过点P作⊙A的切线,切点为Q,则切线长PQ的最小值是

图5
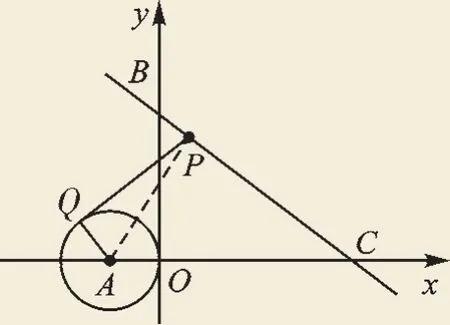
图6
【解析】如图6,作PQ相切⊙A于点Q,连接AP,
∵PQ是⊙O的切线,
∴PQ⊥AQ,∴∠PQA=90°,
∴在Rt△APQ中,PQ2=AP2-AQ2=AP2-1,
∴当AP最小,即AP⊥BC时,PQ最小.
又∵由直线解析式可得C(4,0),B(0,3),
∴BC=5.
∵A(-1,0),
∴AC=5=BC.
又∵∠C=∠C,
∠APC=∠BOC=90°,
易证△CBO≌△CAP,
∴AP=3,∴PQ=2 2.
【点评】此题考查了切线的性质.连接圆心与切点是一条常用辅助线,由此构造出的直角三角形广泛应用于圆的证明和计算中.
例5(2016·湖北荆门)如图7,AB是⊙O的直径,AD是⊙O的弦,点F是DA延长线的一点,AC平分∠FAB交⊙O于点C,过点C作CE⊥DF,垂足为点E.求证:CE是⊙O的切线.

图7
【解析】证明:如图8,连接CO.
∵OA=OC,∴∠OCA=∠OAC,
∵AC平分∠FAB,
∴∠OCA=∠CAE,
∴OC‖FD.∵CE⊥DF,∴OC⊥CE,
∴CE是⊙O的切线.
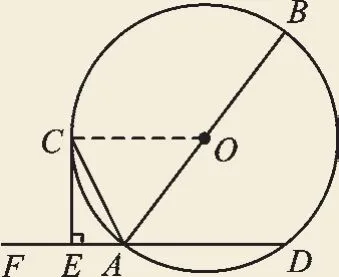
图8
【点评】此题考查了切线的判定.证明切线的常用方法有两种:当已知直线与圆有公共点时,常证明直线经过半径的外端并且垂直这条半径,即“连半径,证垂直”;当题设中未给出直线与圆的公共点时,常证明直线到圆心的距离等于该圆的半径,即“作垂直,证相等”.此题用的是第一种方法.
考点五:与圆有关的计算
主要考查弧长、扇形面积、弓形面积的计算,圆锥的侧面积和全面积的计算.
例6(2016·江苏苏州)如图9,AB是⊙O的直径,AC是⊙O的弦,过点C的切线交AB的延长线于点D,若∠A=∠D,CD=3,则图中阴影部分的面积为

图9
【解析】如图10,连接OC.

图10
∵CD为⊙O的切线,∴OC⊥CD,
∴∠OCD=90°,∴∠D+∠COD=90°,
∵AO=CO,∴∠A=∠ACO,
∴∠COD=2∠A,
又∵∠A=∠D,∴∠COD=2∠D,
∴3∠D=90°,∴∠D=30°,
∴∠COD=60°,
∵CD=3,∴OC=3tan30°=3 ,
∴阴影部分的面积=S△DCO-S扇OCB=
【点评】此题综合性较强,涉及圆中较多的知识.阴影部分面积的求解关键是求出△OCD和扇形OCB的面积.一般情况下,不规则图形面积通常使用割补法求解.
例7(2017·浙江杭州)如图11,在Rt△ABC中,∠ABC=90°,AB=2,BC=1.把△ABC分别绕直线AB和BC旋转一周,所得几何体的底面圆的周长分别记作l1,l2,侧面积分别记作S1,S2,则( ).
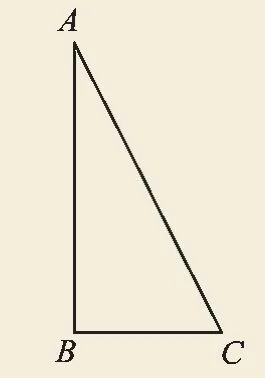
图11
A.l1∶l2=1∶2,S1∶S2=1∶2
B.l1∶l2=1∶4,S1:S2=1:2
C.l1∶l2=1∶2,S1∶S2=1∶4
D.l1∶l2=1∶4,S1∶S2=1∶4
【解析】△ABC分别绕直线AB和BC旋转一周,所得几何体都为圆锥体.
∴l1=2π×BC=2π,l2=2π×AB=4π,
∴l1∶l2=1∶2,
∵S1=π×1× 5= 5 π,S2=π×2×=2π,
∴S1∶S2=1∶2.故选:A.
【点评】此题关键是要认识到△ABC分别绕直线AB和BC旋转一周,所得几何体都为圆锥体,然后再应用圆锥的侧面积公式解决即可.应用公式时,务必弄清楚母线长和底面圆半径是否已知,如果不已知,则需求解后再用公式.

