基于两次傅里叶变换的时域MUSIC波达方向估计

(江西科技学院 信息工程学院，南昌 330098)

1 引 言

宽带信号具有较强的抗干扰能力，在声呐、雷达和通信等领域被广泛应用和分析[1-2]。到目前为止，已有许多学者对基于宽带信号的被动检测和方位估计问题进行了深入研究，并取得了一定的成果[3-5]。近年来，具有高分辨能力的多重信号分类(Multiple Signal Classification,MUSIC)方法得到了快速发展，并在声呐、雷达和通信等领域得到了广泛应用[6-9]。由于频域和波束域 MUSIC方法对数据平稳性的要求限制了其在被动检测和方位估计中的有效应用。如何在付出代价较小的条件下放宽频域和波束域MUSIC方法对数据平稳性的要求，是MUSIC方法应用于宽带目标被动检测和方位估计需要解决的关键问题[10-11]。

针对频域和波束域MUSIC波达方向估计方法在快拍数较少时难以稳定实现目标波达方向估计问题，司伟建等人[12]利用延时相关函数所包含的角度信息，并结合混沌优化思想实现空间谱和波达方向(Direction of Arrival，DOA)估计；张志刚等人[13]利用观测矩阵的结构信息，通过自适应迭代加权，在秩缺失情况下，提高了DOA估计精度；文献[14-16]采用了压缩感知与MUSIC相结合，提高了MUSIC算法在快拍数较少情况下的DOA估计性能；张涛涛等人[17]通过构造基于最佳准则的聚焦矩阵，然后利用滑动平均实现对宽带MUSIC方法改进。以上方法虽然能在快拍数不能满足MUSIC方法要求时提高波达方向估计性能，但均没有给出如何只利用时频处理技术在快拍数不能满足MUSIC方法要求时提高其对DOA的估计性能。为此，本文结合时域常规最佳处理和MUSIC基本思想，提出了一种基于两次傅里叶变换的时域MUSIC波达方向估计方法(本文称之为FTMUSIC方法)。该方法是基于时域与频域相结合的阵列信号处理方法，在一次有效快拍数情况下，通过多个时间点的累积获得良好的协方差矩阵估计，获得与导向权向量稳定正交的噪声子空间，降低快拍数对MUSIC方法的影响，且具有较好的噪声抑制效果，进一步拓宽了MUSIC方法在工程领域的应用。

2 MUSIC方法

MUSIC波达方向估计方法是在噪声(包括干扰)与信号不相关的假设下，对协方差矩阵Rx作特征分解得到信号特征向量Us和噪声特征向量Uv。依据噪声向量与导向权向量的正交性[10-11]，可获得来自扫描角度θ上的空间谱为

(1)

式中：W(θ)=[ej2πfτ1,ej2πfτ2,…,ej2πfτN]为导向权向量;τn=(n-1)dcos(θ)/c，c为声速，d为阵间距。

从MUSIC方法输出空间谱过程可知，MUSIC方法实现时应该满足：信号与噪声不相关，即Rx中不应含有信号与噪声相关成分的贡献；数学上要求Rx满秩；权向量应为复权，以便在目标波达方向获得与噪声子空间的正交性。

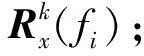
(2)

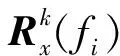
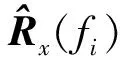
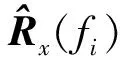
3 FTMUSIC方法

3.1 理论分析

对于时域数据，通常一次快拍即可获得具有信号与噪声不相关和满秩条件的协方差矩阵[18]。若能引入复导向权向量，则可在单次快拍条件下实现DOA估计，进而降低有效快拍数对MUSIC方法估计性能的影响。FTMUSIC方法的基本思路为：通过两次快速傅里叶变换将各阵元时域实数据转换为相移后的复数解析数据，用复数数据引入复导向权向量，再结合时域常规最佳处理求取经相移后协方差矩阵，最后利用特征分解思想求取具有正交特性的噪声子空间，获得来波方向估计值。

假设单个目标信号从θ1方向辐射到N元的阵列上，则第n号阵元接收的实数信号可表示为

xn(t)=s(t-τn(θ1))+vn(t) 。

(3)

式中：τn(θ1)，1≤n≤N为目标信号到达第n号阵元相对于参考阵元的时间延迟，其只与目标信号相对阵列所处的方位θ1有关。

由FFT变换的性质可将式(3)写为频域离散化形式，即

Xn(fm)=S(fm)·exp(-j2πfmτn(θ1)+Vn(fm)。

(4)

由式(4)所示的频域形式也可发现，对阵列接收时域复解析数据进行的时延τn可在频域通过相移的方式来实现，即插入相移因子exp(j2πfmτn(θ))改变各阵元接收数据在扫描角度θ上的相位不一致性。此时，可将式(4)用矩阵形式表达：

XF(fm)=S(fm)·exp(-jφ1)+V(fm) 。

(5)

式中：φ1=[2πfmτ1(θ1)，2πfmτ2(θ1)，…，2πfmτN(θ1)]。

为了求取扫描角度θ方向的空间谱，此时可对处理频带内的频域数据按频率单元乘以相移因子exp(jφ)，改变各阵元接收数据在扫描角度θ上的相位差异，φ=[2πfmτ1(θ),2πfmτ2(θ),…,2πfmτN(θ)]T。此时式(5)可转换为

YF(fm)=XF(fm)·exp(jφ)=XF(fm)·

[exp(j2πfmτ1(θ)),…,exp(j2πfmτN(θ))]T=

XF(fm)Wτ,fl≤fm≤fh。

(6)

式中：fs为系统采样频率，fl为处理频带下限，fh为处理频带上限，Wτ=exp(jφ)。

为了构造时域复解析数据，接下来对式(6)如下处理：

(7)

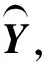
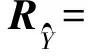
(8)

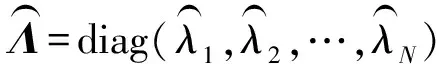
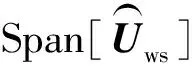
(9)

式中：I1×N=[1,1,…,1]1×N为加法器。

(10)

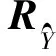
与MUSIC方法相比，FTMUSIC方法所需快拍次数较少。在数据长度满足式(10)情况下，只需一次快拍(包含L采样点数)即可稳定得到具有与目标波达方向对应导向权向量正交特性的噪声子空间。

由于引入了时域解析数据，FTMUSIC方法放宽了对快拍数的条件限制，且不需做子带分解，计算量大大减小，使得FTMUSIC方法有更宽的适用范围。不过，在一个扫描角度上，FTMUSIC方法只有一组子空间，而MUSIC方法相应于每个子带均有一组子空间，子空间个数数倍于FTMUSIC方法。因此，需要数值仿真和实测数据进一步对比FTMUSIC方法和MUSIC方法的噪声抑制及抗干扰能力。

3.2 实现流程

根据上面分析可知，基于FTMUSIC方法的DOA估计方法可分为如下步骤实现：

Step1 对N元阵列采集的时域离散数据xn(m)进行滤波处理，并对滤波后的N路离散数据做一次M点长度的FFT处理，得到相应的频域数据。

Step2 在扫描角度θ上，按式(7)对处理频带内的频域数据乘以相移因子exp(j2πfmτn(θ))。

Step3 对相移补偿后的N路频域数据的共轭形式做FFT，得到时域复解析数据，此时的复解析数据为经过相移后的时域复解析数据。

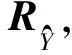
Step5 按式(9)对噪声特征向量进行处理，可获得FTMUSIC方法在扫描角度θ上的空间谱估计值PFTMUSIC(θ)。

Step6 改变扫描角度θ，重复Step 2～ 5，可获得FTMUSIC方法在不同扫描角度上的空间谱PFTMUSIC(θ),θ∈[θl,θh]，θl为扫描角度下限，θh为扫描角度上限。

Step7 通过对PFTMUSIC(θ),θ∈[θl,θh]进行峰值筛选，可对目标波达方向实现估计。

3.3 数值仿真分析

为了进一步验证FTMUSIC方法对有效快拍数的宽容性，对FTMUSIC方法进行数值仿真分析。仿真条件：接收阵为32阵元的等间隔水平直线阵，相邻阵元间距为1 m，模拟信号为700～800 Hz宽带高斯白噪声，信号长度0.1 s，SLR(Spectrum Level Ratio)为信号与背景噪声谱级比，背景噪声为加性高斯白噪声，模拟信号输入方向为60°。系统采样率为20 kHz，一次采样长度为1 s，FTMUSIC方法由一次快拍实现，MUSIC方法所分子带数为M=100，每一子带由76次快拍(每一次快拍包含512个采样样本)实现。

图1为SLR=-25～0 dB情况下，由MUSIC方法与FTMUSIC方法通过200次独立统计所得正确检测概率。图2为SLR=-25～0 dB情况下，由MUSIC方法与FTMUSIC方法通过200次独立统计所得DOA估计均方误差(Root Mean Squared Error,RMSE)。图3为SLR=-15 dB情况下，由MUSIC方法与FTMUSIC方法所得单一时刻空间谱。

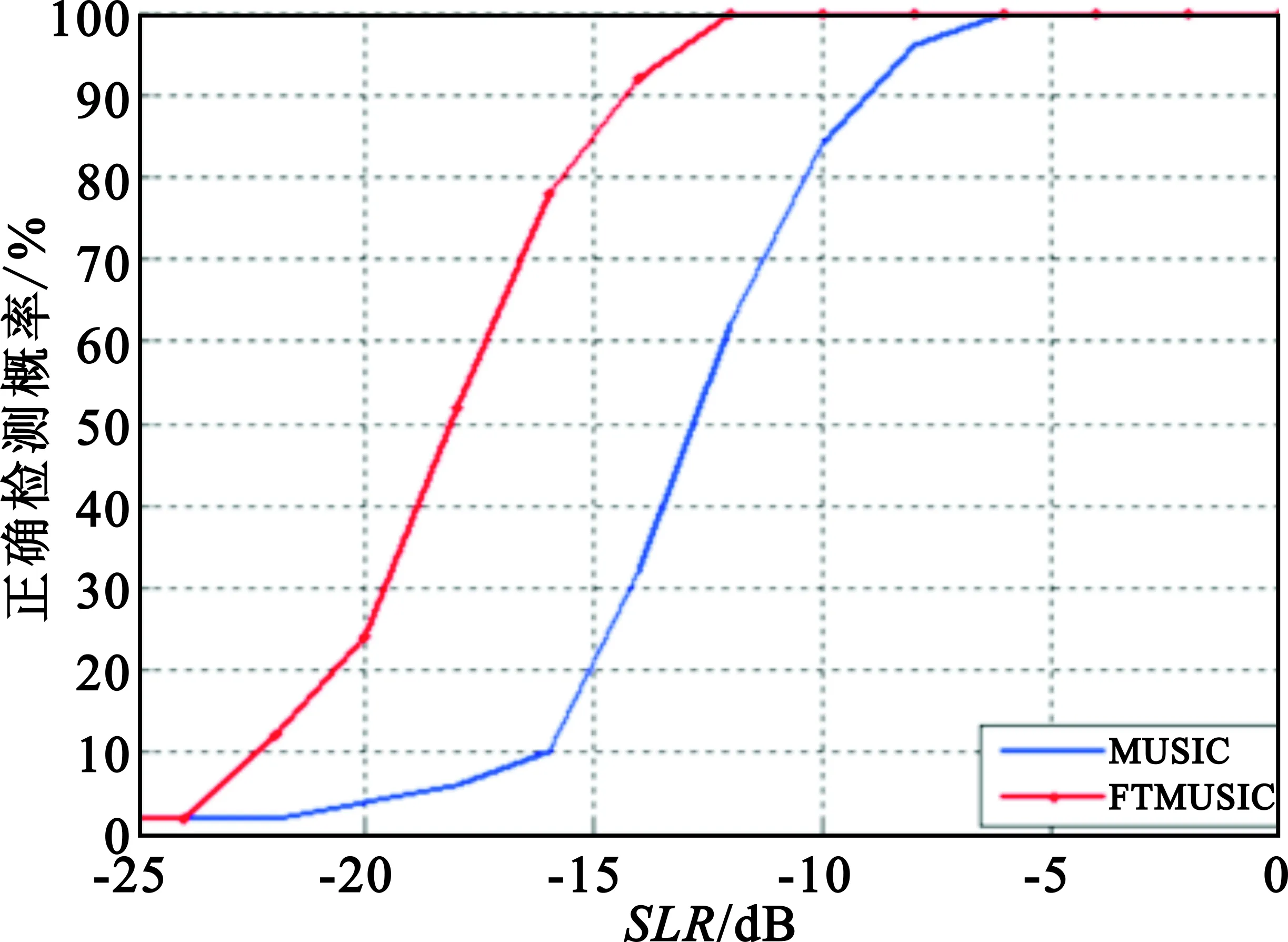
图1 MUSIC与FTMUSIC检测目标成功率Fig.1 Detect target success rate of MUSIC and FTMUSIC

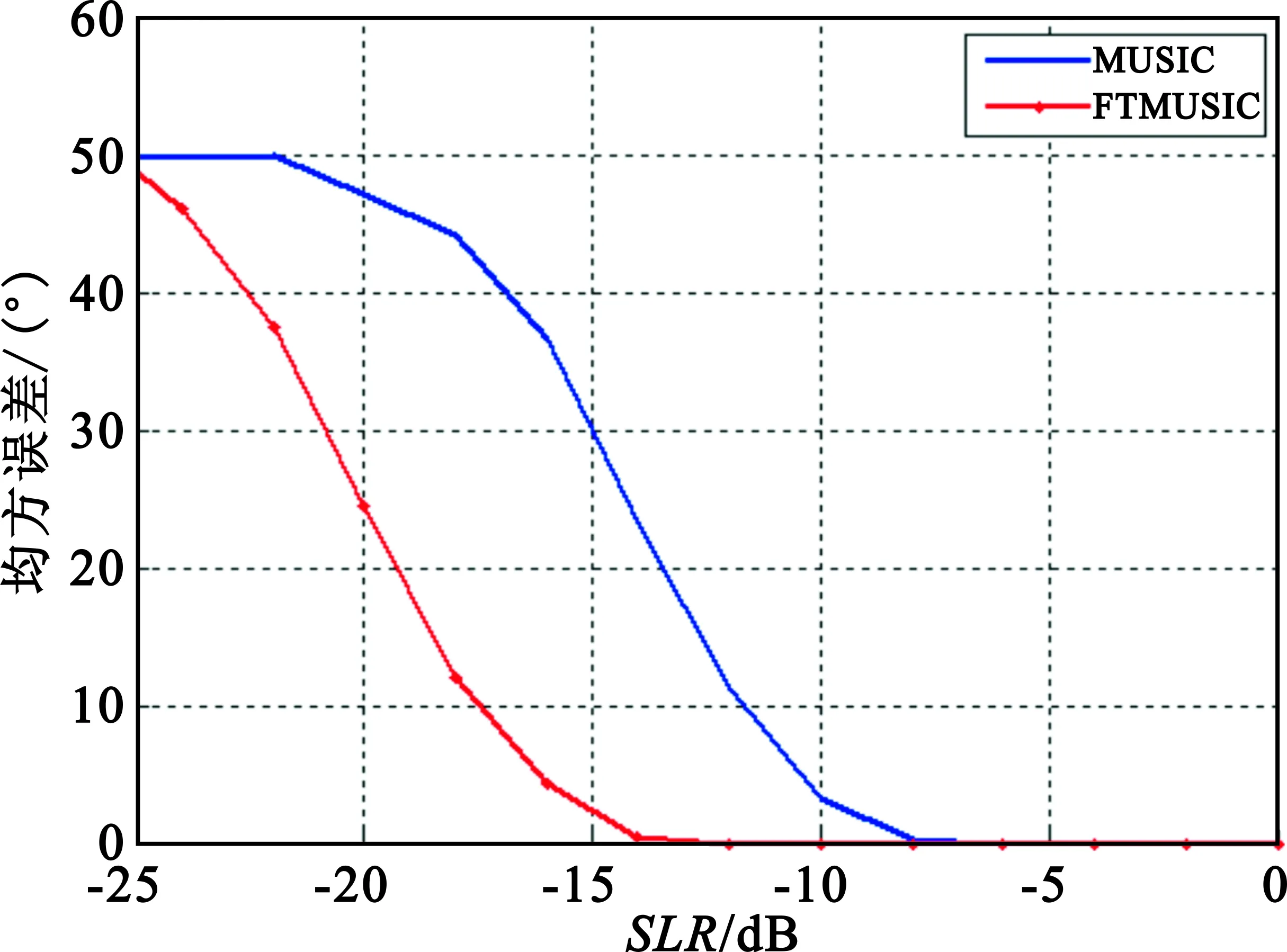
图2 MUSIC与FTMUSIC波达方向估计均方根误差Fig.2 RMSE of DOA estimation of MUSIC and FTMUSIC

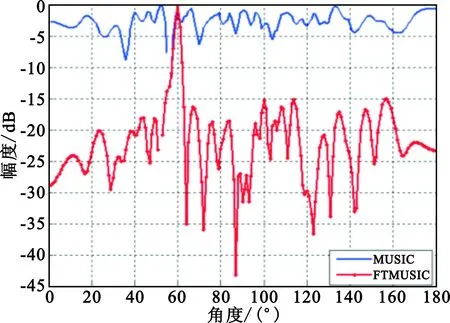
图3 2种方法输出空间谱

由图2和图3仿真结果可知，在有效快拍数较少情况下，对于相同的正确检测概率和DOA估计精度，相比MUSIC方法，FTMUSIC方法输出空间谱对最低信噪比要求上降低了5 dB，背景噪声级和旁瓣级得到了3 dB以上的改善，数值仿真结果进一步证明了FTMUSIC方法对有效快拍数的宽容性得到了有效改善。

在该数值仿真数据处理中，FTMUSIC方法与频域MUSIC方法计算量比较是在Intel(R) Core(TM) i7-7500U CPU@2.70 GHz 2.90 GHz的计算机上利用Matlab2014a的CPU TIME测出的，如表1所示。该实验采样率较高，由于FTMUSIC方法只对一次快拍数据进行处理，且并未进行子带分解，其计算量小于频域MUSIC方法。

表1 两种方法计算时间比较Tab.1 Comparison of processing time of two methods

4 实测数据处理

为进一步考核FTMUSIC方法性能，下面分别利用FTMUSIC方法和MUSIC方法对某次试验数据进行处理并作对比。试验中，接收阵为均匀分布32阵元的水平直线阵，阵元间距为8 m；处理数据带宽为60～120 Hz，处理数据时间长度为100 s，该时间段内目标方位在33°、50°、55°、69°、77°(运动)、82°、109°和153°(运动)附近。MUSIC方法具体处理过程如下：首先将数据分块，每块数据为1 024个，记为一次快拍样本长度，数据块之间重叠512个，快拍数为76，做FFT后选取60～120 Hz频段，对每个频点分别作协方差估计；而FTMUSIC方法通过512阶带通滤波器选取60～120 Hz频段，采用一次快拍数据进行分析处理。图4和图5分别为MUSIC方法和FTMUSIC方法处理数据所得时间历程图，图6为单一时刻两种方法输出空间谱。

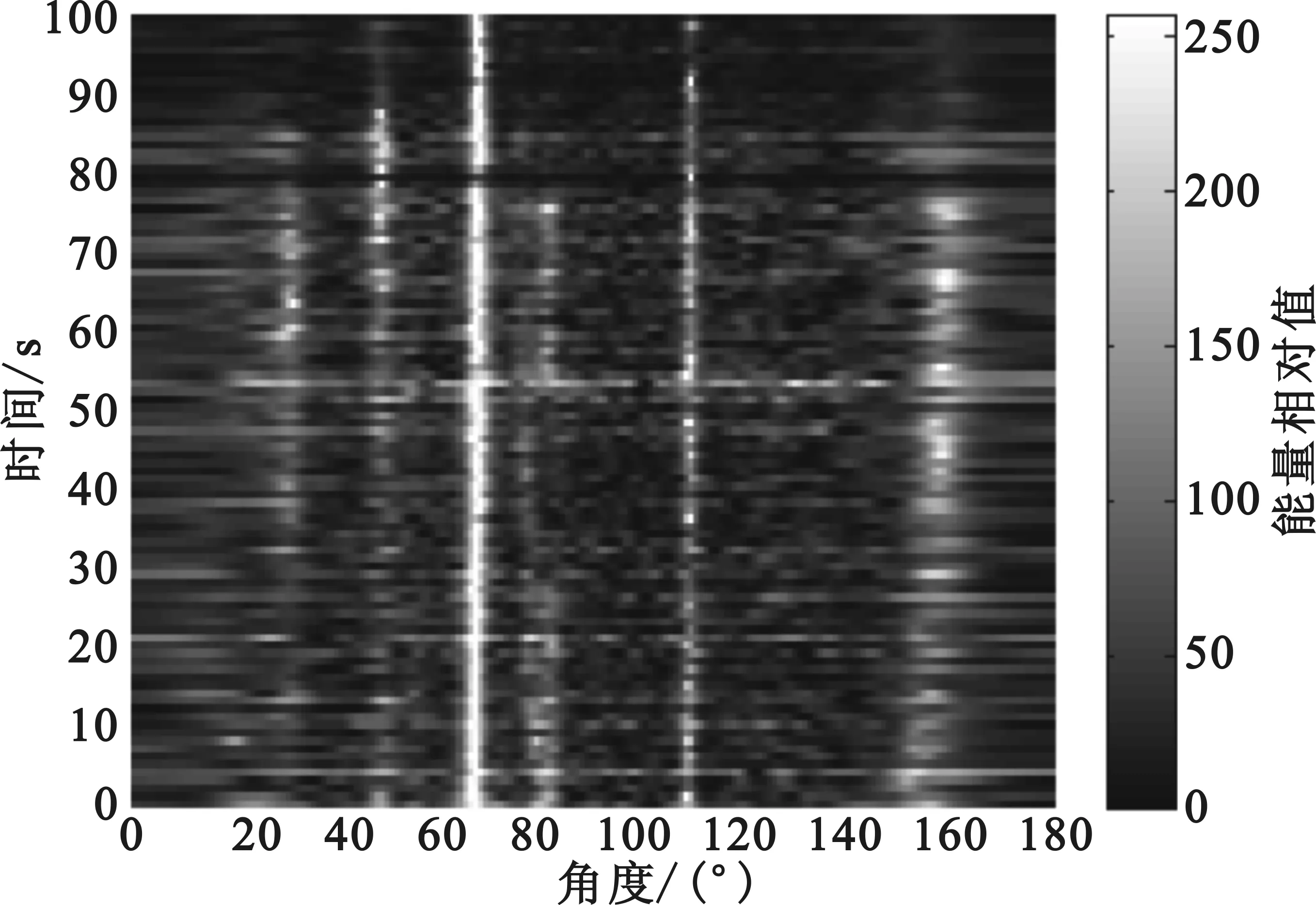
图4 MUSIC方法所得方位历程图Fig.4 Bearing time/record of MUSIC method

图5 FTMUSIC方法所得方位历程图Fig.5 Bearing time/record of FTMUSIC method

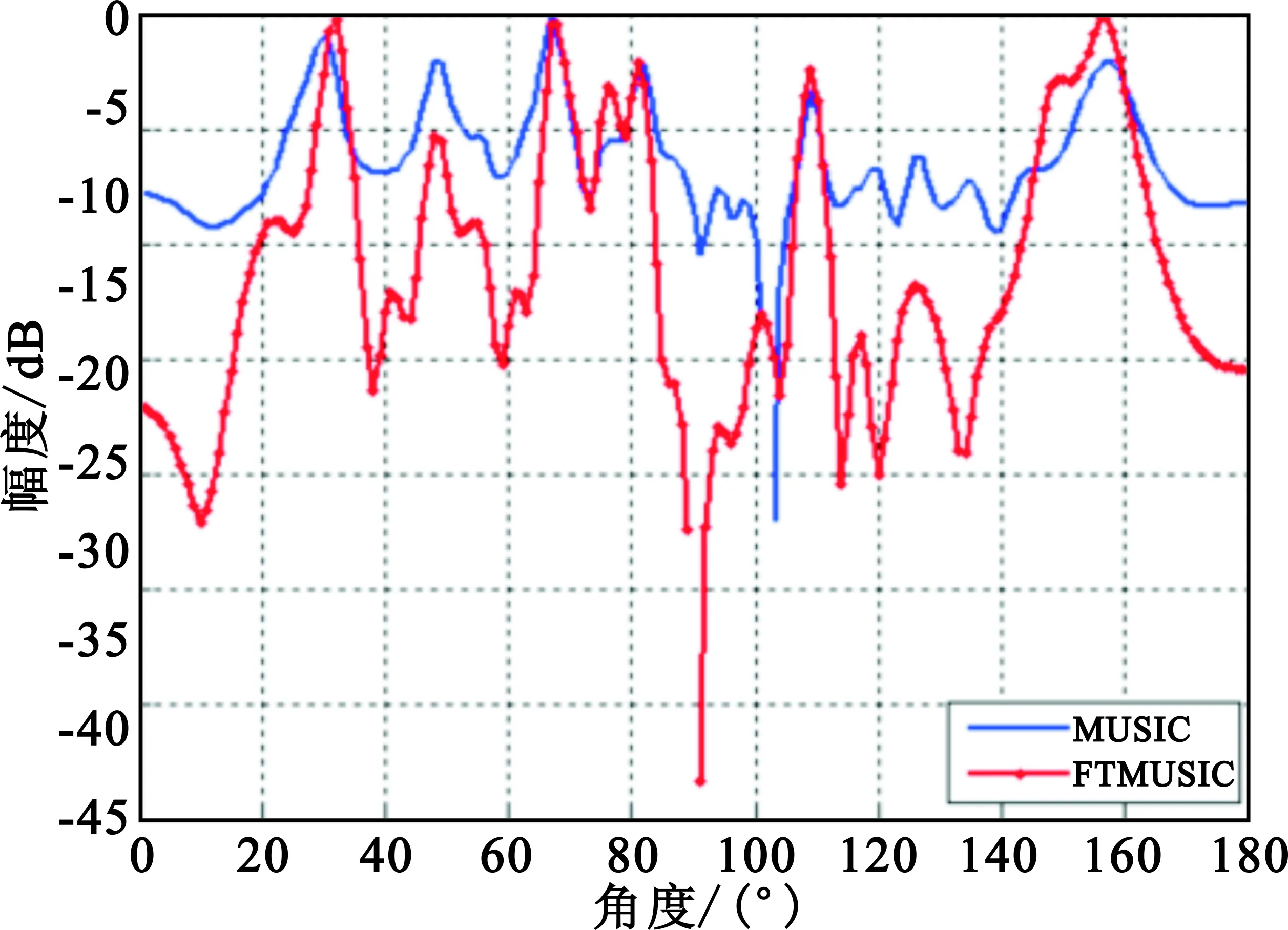
图6 两种方法输出空间谱(t=60 s)Fig.6 Output spatial spectrum of two methods(t=60 s)

由图4～5可知，FTMUSIC方法所得方位历程图显示目标航迹清晰，目标方位明晰可辨，进一步证明了FTMUSIC方法在理论上和实测数据处理上的正确性；而MUSIC方法在0～100 s时间段内无法对55°附近目标实现有效检测，对77°附近目标检测效果较差，且无目标处谱级较大。

同样，由图6也可以看出，FTMUSIC方法较MUSIC方法有更低的背景噪声级和旁瓣级。

5 结束语

本文首先介绍了频域MUSIC波达方向估计方法基本原理，并分析了频域MUSIC方法对快拍数的需求，然后提出了一种基于两次傅里变换的时域MUSIC波达方向估计方法——FTMUSIC方法。该方法是基于时域与频域相结合的阵列信号处理方法，利用两次傅里叶变换实现了时域复解析数据构造和相移补偿，在一次有效快拍数情况下通过多个时间点的累积可获得良好的协方差矩阵估计，可获得与导向权向量稳定正交的噪声子空间，降低了快拍数对MUSIC方法的影响，且具有较好的噪声抑制效果，进一步拓宽了MUSIC方法在工程领域的应用。数值仿真及实测数据处理结果均表明，在有效快拍数较少情况下，相比频域MUSIC方法，对于同样的正确检测概率和DOA估计精度，FTMUSIC方法输出空间谱对最低信噪比要求上降低了5 dB，背景噪声级和旁瓣级得到了3 dB以上的改善，目标检测和方位估计性能得到了明显提高。

如何在FTMUSIC方法基础上进一步降低一次快拍包含的采样点数还有待进一步研究。