基于无速率码的遥感数据自适应传输技术

宋 鑫，廖育荣b，丁 丹b，杨新岩，曾江辉

(航天工程大学 a.研究生院；b.电子与光学工程系，北京 101416)

1 引 言

随着有效载荷技术的发展，遥感卫星所获取的数据量急剧增加。地面对卫星的可视时间十分有限，而固定编码调制方式的传输速率恒定，有限时间内的传输数据量难以满足地面系统要求。为了及时有效地将卫星采集到的海量遥感数据传输至地面站，文献[1-2]采用了第二代数字卫星电视广播标准(DVB-S2)中的自适应编码调制(Adaptive Coding and Modulation,ACM)[3]方案，根据信道状态的变化情况自适应地切换编码调制方案，实现了传输数据量的提升。该ACM方案采用BCH码和LDPC码级联的编码方案，可选码率有1/4、1/3、2/5等，可选调制方式有QPSK、8PSK、16APSK等。但是ACM方案也存在固有的问题：一是接收端需要计算信道状态信息并反馈给卫星，信道状态计算误差以及反馈时延会造成星上切换的编码调制方案与地面终端不匹配；二是在信道状态变化较快时，地面终端需要上传大量的反馈信息，这会造成链路资源浪费并且使得星上过于频繁地切换编码调制方案；三是在“阶梯式”的切换方案下，链路余量仍未得到充分利用。

针对上述问题，本文利用ACM方案中码率可变的思想，结合无速率码[4]固有的随机性和信道自适应特性，采用了基于无速率码的遥感数据传输技术。无速率码作为一种特殊的信道编码，最初作为纠删编码使用，但文献[5-6]证明，无速率码作为纠错编码使用时也具有良好的性能。无速率码的自适应特性主要体现在码率随信道状态的变化自适应地进行无缝调整，非常适合应用于时变的无线信道中实现高效、可靠的数据传输。

文献[7]设计了一种无速率码链路传输协议，提出了译码累积分布函数的概念，将其定义为不同长度的编码数据对应的成功译码概率，并利用动态规划的方式确定下一次发送时的最优编码长度。但是文献[7]没有将无速率码应用至星地数据传输中，也未对码率的自适应变化进行仿真验证。文献[8]设计了一种基于无速率码的自适应算法以调整无速率码的传输码率，文献[9]在文献[8]的基础上引入余量因子、平均重传次数、信道加权系数等参数对自适应算法进行约束和优化，提高了算法的可行性。但是文献[8-9]中对调制方式的设置较为单一，预设的最低信噪比也在4 dB以上，对低信噪比下的传输情况考虑不足。

现有文献中侧重于对传输机制和策略的设计，未对传输过程中有效数据率和传输数据量进行分析和处理，也未对低信噪比和多种调制方式下的传输情况进行考虑。针对上述问题，本文提出将无速率码与QPSK、8PSK、16QAM、64QAM等调制方式相结合进行遥感数据传输，并将低信噪比时的情况也考虑在内。本文方法与文献[2]的分析方法类似，但与文献[2]相比，本文在参数选择和数值计算时纳入了无速率码的译码环节，根据无速率码的译码成功概率对码率值进行设置，并且可在单一调制方式下仅利用无速率码的无缝调整实现传输数据量的提升。

2 基于无速率码的自适应传输方案

2.1 传输方案

采用无速率码进行遥感数据传输的基本思想是在信道状态快速变化时，接收端利用无速率码自适应地调整参与译码的比特数，使得码率发生变化，从而保持误比特率恒定。基于无速率码的遥感数据传输方案如图1所示。

图1 采用无速率码的自适应传输方案Fig.1 The adaptive transmission scheme using rateless codes

完整的数据传输过程包含5个步骤：

Step1 地面终端通过上行链路注入成像需求。

Step2 遥感卫星获取影像信息，对影像数据完成在轨处理。

Step3 对生成的信息产品进行无速率编码，将编码后的数据加工成适用于星地传输的数据包。

Step4 遥感卫星将Step 3中的若干组数据包通过下行链路实时传输至地面终端，终端接收到数据后即刻启动译码。

Step5 地面终端对一组数据包成功译码后，通过上行链路反馈确认信息(Acknowledgement,ACK)给星上，卫星开始传输下一组数据包，直至所有数据包都被终端成功接收，本次数据传输结束。

在整个传输过程中，地面终端不必进行信噪比估计，也不需要向卫星反馈信道状态信息，只需要在每组数据包接收完成后向卫星发送1 bit左右的ACK信息，相比ACM方案而言所需的反馈信息极少，减少了反馈时延带来的空闲期。卫星也不必在多种编码调制方案之间进行切换，只需要源源不断地向终端传输数据，直到接收到终端上传的ACK信息，这样就提升了信道利用率，简化了卫星工作模式。

2.2 无速率码的选择及参数设置

Luby提出的LT码是第一种实用的无速率码，但LT码在加性高斯白噪声(Additive White Gaussian Noise,AWGN)信道下存在明显的误码平台[10]。Shokrollahi提出的Raptor码[11]也是一种典型的无速率码，在编码时一般将一个弱化的LT码作为内码，在此基础上增加了一个预编码(通常采用高码率的LDPC码)，因此Raptor码实际上是一种级联码。由于采用了级联结构，预编码部分可以进一步纠正LT码译码结果中的差错，从而有效降低了误码平台。因此，本文传输方案中的无速率码设定为Raptor码。

Raptor码具有前向递增冗余特性，可以利用之前的译码信息对新接收到的编码数据进行初始化，称之为“渐进”译码模式，这样可以在不损失译码性能的前提下，进一步降低译码复杂度。Raptor码实际上是利用LT码部分实现“渐进”译码，设译码成功时LT码的编码长度为n，LT码输入信息长度为k，定义译码开销为ε=n/k，LT码的码率为rLT=k/n，两者互为倒数。遥感卫星过境时链路传输损耗的变化会引起接收端符号信噪比Es/N0的变化，Raptor码在每个信噪比下选取不同ε值时的译码成功概率Ps不同。但Ps与ε之间的关系受到调制方式、信噪比、预编码种类、度分布函数、信息比特数长度等的影响，目前尚无确切的关系式可以表示两者之间的关系。为了选取最佳ε值，本文对Raptor码在不同调制方式和不同信噪比下的译码情况进行蒙特卡洛仿真，将每个信噪比对应的所有ε值从小到大排列并分别统计各ε值出现的频率，将各频率值依次累加作为相应ε值下的译码成功概率。根据大数定律可知，当大量重复某一实验时，最后的频率无限接近事件概率，因此上述分析是合理的。

对Raptor码在不同信噪比下的译码性能进行仿真分析。Raptor码的预编码采用码率为0.95的LDPC码，输入信息比特数s=19 000，构造校验矩阵时采用PEG算法，固定变量节点度数α=3，校验节点近似具有规则的度数β=60；内码为LT码，其度数分布为

Ω(x)=0.015x+0.495x2+0.167x3+

0.082x4+0.071x5+0.049x8+

0.048x9+0.05x19+0.023x66。

(1)

仿真采用联合译码算法[12]，并在“渐进”模式下进行，在联合译码算法中设置迭代次数的值为(30,30,10)。发送端采用QPSK、8PSK、16QAM以及64QAM共4种调制方式，信号功率归一化为1 W，设置信噪比变化范围为[-5,10] dB。采用蒙特卡洛仿真(仿真次数设为10 000次)，得到采用上述4种调制方式时各信噪比下不同ε值对应的译码成功概率，部分结果如图2所示。进一步设定Pth=99.7%为阈值，选取Ps≥Pth时所对应的最小ε作为最佳ε值，并根据ε与rLT的关系求得最佳码率值。

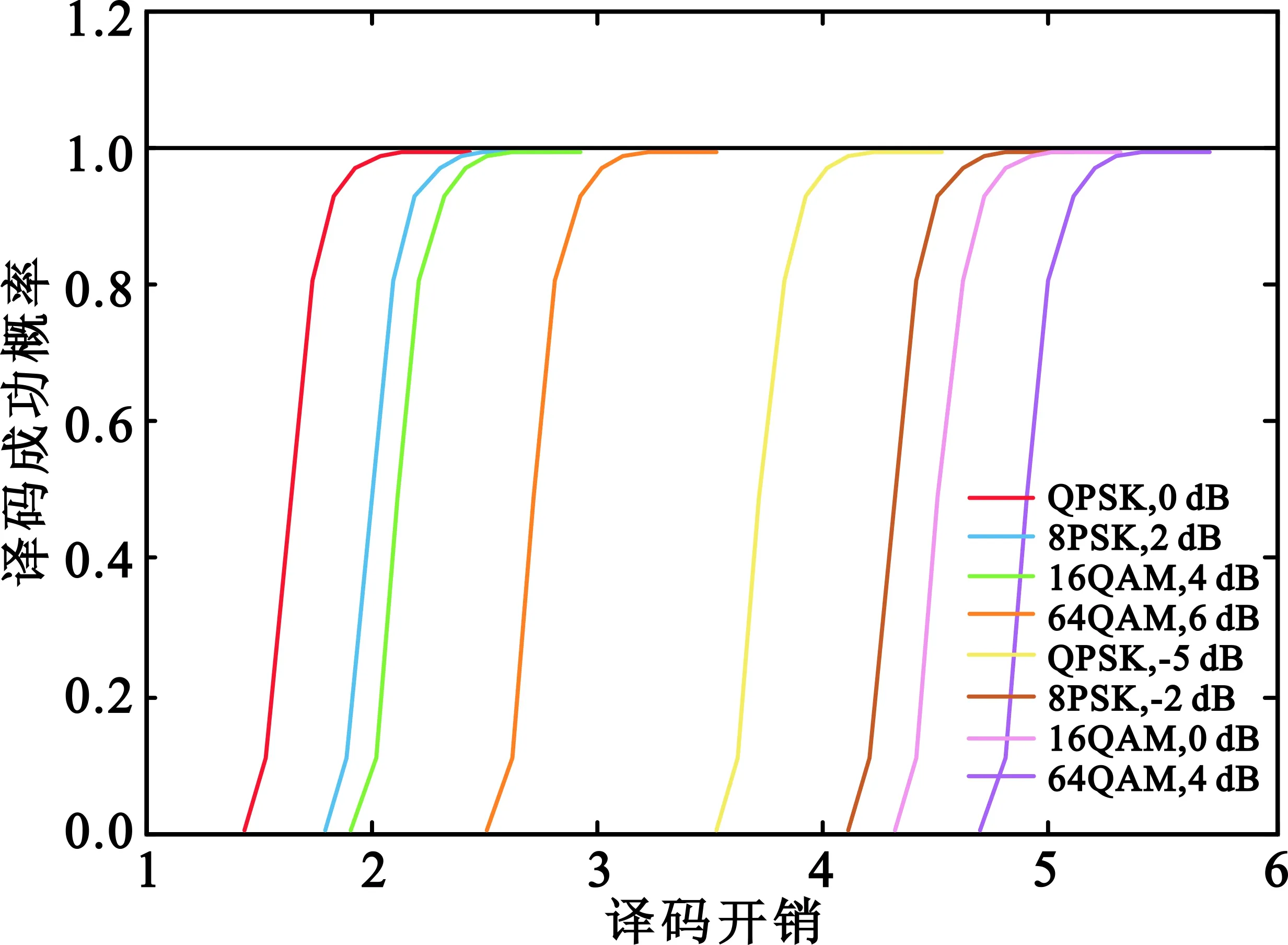
图2 Raptor码的译码开销与译码成功率关系图(部分)Fig.2 The relation diagram of decoding overhead and decoding success probability of Raptor code

需要说明的是，虽然通过无限增加编码长度可以保证Ps等于1，但是过多的编码数据会增加接收端译码复杂度并降低码率值，使得有效数据率下降。因此本文通过设定阈值的方式在Ps与ε之间进行折中，且设定的阈值Pth为99.7%，几乎逼近1，已经确保了系统具有极大的概率可以成功译码。另外，通过与重传机制[8]结合，总可以使得系统在该ε下具有良好的译码性能。

3 链路计算与传输数据量分析

3.1 星地传输链路的计算

为了计算采用无速率码的系统在卫星过境时的传输数据量，需要先对星地传输链路进行计算与分析。在星地传输链路的计算中，通常使用接收机输入端的载噪比C/N0来衡量信道的好坏，其中C为载波功率，N0为噪声功率谱密度。下行链路计算方程为

[C/N0]=[EIRP]+[G/T]-[L]-[M]+228.6。

式中：方括号表示取对数；EIRP是卫星发射天线的等效全向辐射功率，用来表征星上发射的载波功率的大小；G/T是地面接收天线的品质因数；L是链路传输损耗；M是系统备余量；常数值228.6为玻尔兹曼常数取对数后的结果。

在卫星过境期间，链路传输损耗L随着星地传输距离的缩短而减小，从而引起了接收端载噪比C/N0的增加。不同传输距离都将对应一个最佳传输码率值以及最大有效数据率，无速率码的作用就是通过其自适应特性实现不同码率之间的无缝切换。

3.2 Raptor码在不同调制方式下的码率

以采用联合译码算法的Raptor码为例，对无速率码在信噪比变化时的码率值进行求解。设成功译码时的码率值为r=rprLT，其中rp为预编码的码率，本文中为0.95。在2.2节中得到了不同调制方式下Raptor码在Es/N0的值为[-5,10]dB时的最佳译码开销ε，根据式(3)可以计算得到相应的码率值，结果如表1所示。

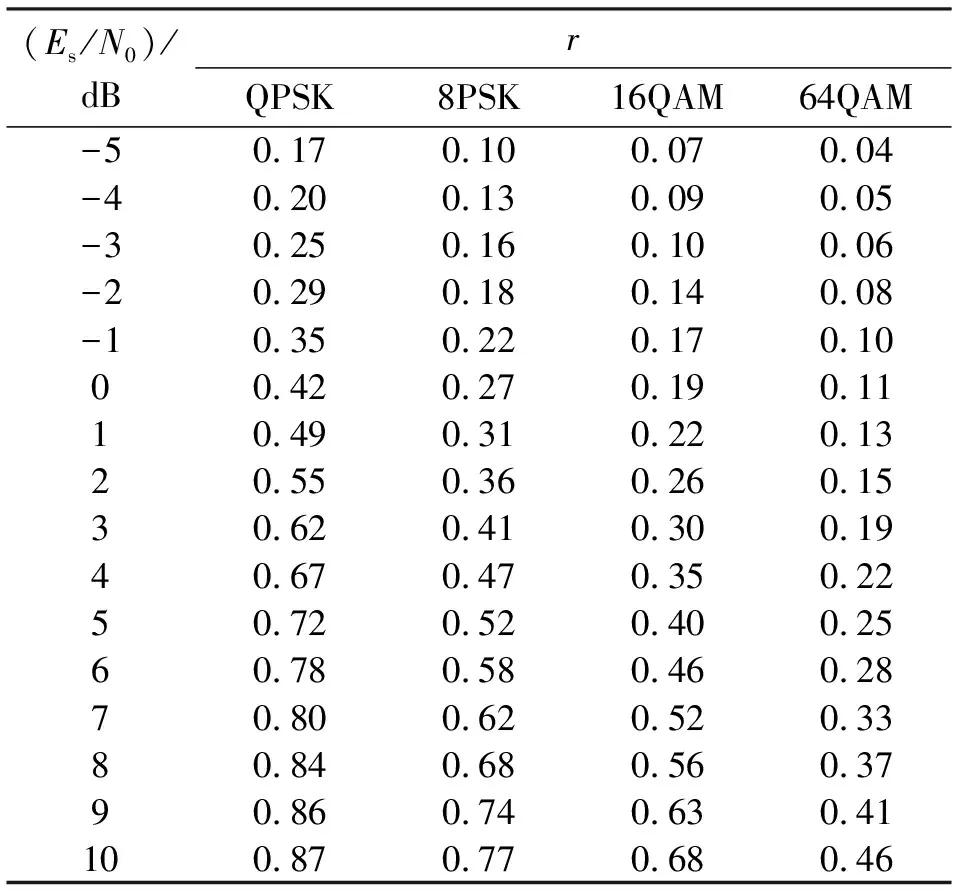
(3)

基于上述分析，将遥感卫星的主要参数设置如下：轨道高度为400 km，EIRP值为15 dBW，符号速率Rs=30 Msymbol/s，载波频率为7.25 GHz，地面终端G/T为27.6 dB，系统备余量为3 dB。为简单起见，暂不考虑滚降系数的影响。

在以上参数条件下可以仿真得到卫星从进站至过顶的过程中，接收端载噪比C/N0的变化范围约为[73,88]dB，根据式(4)可求得接收端信噪比Es/N0的变化范围约为[-5,10] dB。

[Es/N0]=[C/N0]-10lg(Rs)。

(4)

表1求得的r是Es/N0为整数值时的码率值，但卫星过境时接收端信噪比是连续变化的，如果要真正实现不同码率之间的无缝切换，还需要确定Es/N0在区间[-5,10] dB内任意一点的码率值。针对这个问题，考虑利用上述计算出的码率值r进行多项式拟合，以最小均方根误差为约束条件，确定最佳拟合阶数为7阶，表达式为

(5)

式中：an为拟合参数。根据表1中的仿真数据得到拟合参数如表2所示，拟合曲线如图3所示。

图3 采用不同调制方式的码率拟合曲线Fig.3 The code rate fitted curve withdifferent modulation schemes

表2 不同调制方式的拟合参数(部分)Tab.2 The fitting parameters with different modulation schemes

上述分析得到了信噪比与码率值的关系，进一步可以求出有效数据率随信噪比的变化情况，将有效数据率乘以卫星过境时间就得到了数据传输量。在过顶时刻将卫星从进站至出站的过程划分为两个阶段，信噪比的变化情况是完全对称的，两个阶段中码率、有效数据率、传输数据量的计算方法和结果完全相同，因此这里只对卫星从进站至过顶的过程进行分析。如果将卫星从进站至过顶的过程按等间隔信噪比进行阶段划分，会导致每个阶段内卫星运行时间不相同，使计算变得复杂。针对这个问题，考虑采用等间隔中心角进行阶段划分，这样得到的各阶段的运行时间T是相同的，然后求解出有效数据率曲线的积分值Q，则QT即为传输数据量。图4给出了中心角与仰角的关系图，其中δ为中心角，θ表示仰角。将卫星运行过程按照中心角间隔为1°进行阶段划分，以卫星所处阶段为横坐标重新画出码率值的变化情况，如图5所示。其中，两个横坐标值之间包含两个阶段，比如11～13对应的是阶段11和12。

图4 卫星运行过程中仰角和中心角的关系图Fig.4 The relation diagram of elevation angle and center angle during the operation of the satellite

图5 卫星过境时段内码率变化趋势Fig.5 The code rate behavior during satellite transit process

3.3 传输数据量计算

假定遥感卫星和地面终端按照2.2节中给出的方式进行编码和译码，则计算传输数据量时就可以参照2.2节及3.2节中的结论。为了便于与文献[2]中的ACM方案进行对比，假设在当前码率下数据包均一次性传输成功，在计算时暂不考虑传输时延和地面终端反馈ACK信息带来的空闲期。对采用Raptor码的系统而言，卫星在运行过程中任意位置处的有效数据率为

Rb-Rap=Rs·lb(M)·r。

(6)

式中：M为调制阶数，Rs为符号速率，r为该位置处的码率值。

参照文献[2]在表3中给出了适用于本文中系统的ACM方案。需要说明的是，阶段1～6中的信噪比均小于基于DVB-S2标准的ACM方案中给出的可以进行数据传输的最低符号信噪比，因此没有满足条件的编码调制组合，不进行数据传输。

表3 基于DVB-S2的ACM方案Tab.3 The ACM scheme based on DVB-S2 standard

ACM方案中有效数据率Rb-ACM的计算方式与Rb-Rap相同，进一步得到Rb-Rap与Rb-ACM的变化情况如图6所示。可以看出，随着仰角的增加，采用Raptor码的系统在4种调制方式下的有效数据率不断增加，并且实现了无缝切换。这表明，与ACM方案相比，采用无速率码的传输方案能进一步利用“速率阶梯”之间的信道余量进行数据传输，从而提高了遥感卫星数据传输的频谱效率。

在3.2节中设置的参数下，1°中心角对应的卫星运行时间为T=15.02 s，求出图6中各曲线与横坐标的积分值Q，则QT就是数据传输量D。表4中给出了几种方案下的传输数据量，图7给出了卫星过境期间累计传输数据量的情况。

表4 几种方案的传输数据量Tab.4 The data amount of different schemes

图7 卫星过境时段内累计传输数据量Fig.7 The accumulated data amount during satellite transit process

令DM-Rap表示调制阶数为M时Raptor码系统的传输数据量，根据表4中的数据可知，D4-Rap、D8-Rap、D16-Rap、D64-Rap分别比DACM提高了10.29%、21.30%、27.65%、20.70%，这表明采用无速率码的传输方案在信道状态条件极差且变化范围较大时更具优势。4种方案中，D64-Rap小于D16-Rap，因为与其他3种方案相比，采用64QAM的方案在相同信噪比下成功译码所需要的冗余比特最多，因此码率最低，从而引起传输数据量的下降。但在其他3种方案中，通过增加星座点个数及其包含比特数，足以弥补初始阶段码率偏低引起的传输数据量的损失，这说明经过恰当的设计，总能使得采用无速率码进行遥感数据传输时的数据量达到最大。

图8给出了本文4种传输方案和ACM方案在卫星过境时段内的频谱效率，为便于观察和对比，将横坐标设置为信噪比。可见，在采用无速率码进行遥感数据传输时能够进一步挖掘ACM方案中“阶梯”之间的链路余量，使频谱效率随信道状态的变化而无缝变化，充分利用了卫星信道的传输能力。从图8中还可以看出，ACM方案共进行了5次切换，而本文方案仅在单一调制方式下即可进行数据传输，且得到比ACM方案更多的传输数据量，进一步体现了采用无速率码进行数据传输的优势。

图8 采用不同传输方案的频谱效率曲线Fig.8 The spectrum efficiency curve with differenttransmission schemes

4 结束语

无速率码具有信道自适应特性，在信道状态变化较快时更具有优势，非常适合应用于遥感数据传输系统中。与DVB-S2标准中的ACM方案相比，采用无速率码的方案频谱效率更高，且不必进行信道状态的估计和反馈，有效降低了系统的复杂度，节省了大量的反馈开销。本文以Raptor码为例，提出了无速率码与4种调制方式相结合的传输方案，给出了在译码成功概率Ps≥99.7%的性能目标下不同调制方式和不同信噪比下的译码开销和码率，进而根据链路预算结果，求解了卫星过境期间的有效数据率和传输数据量，并与ACM方案进行了比较。仿真和分析结果显示，采用Raptor码的传输方案能将传输数据量进一步提高10.29%～27.65%，从而验证了该方案的正确性和有效性。

本文主要考虑的是不同调制方式下Raptor码译码开销的求解以及卫星过境期间传输数据量的计算，在将来的研究中，可以进一步考虑传输机制和策略对码率值、传输数据量的影响。