大规模天线组阵信号并行合成方法

(1.航天工程大学 电子与光学工程系，北京 101416；2.西昌卫星发射中心，四川 西昌 615606；3.西安卫星测控中心，西安 710043)

1 引 言

SUMPLE算法由于实现较简单、运算量合理、合成效率高，是天线组阵合成最重要算法之一[1-4]。信号合成器需要接入所有天线的接收信号，并同时对所有天线信号进行权值计算。当天线组阵规模较大时，会带来两个问题：一是很难将所有天线的接收信号同时传输至信号合成器；二是受限于单个信号处理设备的处理能力，信号合成器很难同时对所有天线接收信号进行权值计算和合成。因此，限制了SUMPLE算法在大规模天线组阵中的应用。在通用计算平台上进行信号处理已经得到了应用[5-7]，为大规模天线组阵的信号合成提供了新思路。典型的通用计算平台是中央处理器(Central Processing Unit，CPU)和通用图形处理器(Graphics Processing Unit，GPU)异构系统[8-10]，本文对CPU-GPU异构系统上的并行合成方法进行研究。

国内对天线组阵并行合成方法的研究比较少。文献[11]提出了两种SUMPLE算法的分级实现方法，分别是全增益和部分增益实现方法。其基本原理是将所有天线分为若干天线组，首先在天线组内合成，然后将不同天线组的合成信号继续合成，降低了需要同时传输至信号合成器的信号路数，避免了信号合成器同时对所有天线进行合成。不足之处是部分增益法存在信噪比(Signal-to-Noise Ratio,SNR)损失，也没有对两种方法在CPU-GPU异构系统上的可行性进行分析。

本文将文献[11]提出的全增益实现方法称为多天线组合成方法(Multi Antenna Group Method,MAGM)，详细研究了该方法的实现步骤，对其在CPU-GPU上的可行性进行分析。提出了一种多信号块合成方法(Multi Signal Block Method,MSBM)，基本原理是将同一积分段内的所有天线信号发送到一个节点进行处理，不同节点处理不同积分段的信号，如此便可延长每个积分段的信号传输时间和处理时间，降低各处理节点的数据传输速率，减小各处理节点的计算压力。MSBM同时处理不同积分段的信号，而广泛应用的SUMPLE算法通过前一个积分段的权值推算当前积分段的权值，必须按照时间先后顺序依次处理，不能满足要求。本文研究了SUMPLE算法的积分段内迭代方法，消除了权值计算的时间依赖，并仿真分析了其合成性能。

2 SUMPLE算法基本原理

设定天线组阵系统由Nant个天线组成，各天线接收信号可表示为

Si,k=si,k+ni,k,i=1,2,…,Nant。

(1)

式中：下标k和i分别表示时间序号和天线序号，si,k、ni,k和Si,k分别表示第i个天线k时刻的信号、噪声和含有噪声的信号。信号合成时的权值系数可表示为

Wi,K=wi,K+ηi,K,i=1,2,…,Nant。

(2)

式中：下标K是以积分段为单位的时间序号，wi,K是理想权值，ηi,K是由噪声引起的权值估计误差。

SUMPLE算法将每个天线接收信号与其他所有天线的加权和进行相关，得到复权值，进而对所有信号进行加权合成。第i个天线的第K+1个积分段的权值Wi,K+1由Wi,K递推得到：

(3)

式中：L是积分段的采样点数；上标*表示复共轭；RK+1是归一化幅度因子，满足

(4)

常用的SUMPLE迭代发生在积分段之间，本文称为积分段间迭代方法，如图1所示。第K+1个积分段权值由第K个积分段的权值递推得到，这使得必须按照时间先后顺序计算不同积分段的权值，约束了算法的并行性。

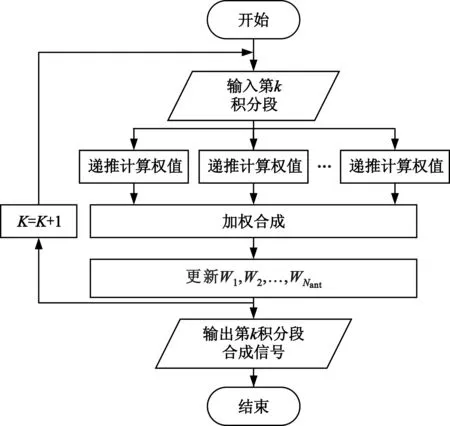
图1 SUMPLE算法的积分段间迭代方法Fig.1 Iterative method between the integral time intervals

3 并行合成方法

本文根据并行分解原理不同，将并行合成方法分为MAGM和MSBM。MAGM基于任务分解原理，通过将大量天线合成任务分解为多个天线组的合成任务，相当于将一个复杂任务分解为大量可并发执行的子任务。MSBM基于数据分解原理，将信号流分解为多个相对独立的信号块，并发处理信号块。下面对这两种方法及其实时性进行分析，分析采用以下参数：天线数量为500；接收信号采样率为100 MHz，12 bit采样；采样积分段长度为1×105，时长为1 ms。GPU 型号为TESLA K80，双精度浮点性能为2.91 Tflop；在现有PCI-e3.0总线条件下，其带宽为16 GByte/s。

3.1 多天线组合成方法

将所有天线分为若干天线组，首先在天线组内合成，然后将不同天线组的合成信号继续合成。合成器分为一级合成器、二级合成器等多级合成器。MAGM的基本原理如图2所示。

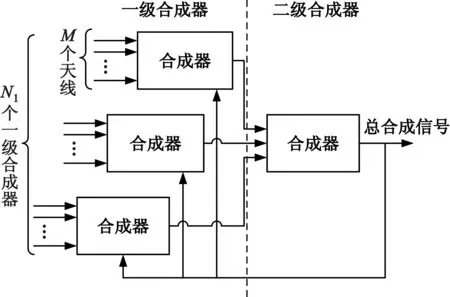
图2 MAGM的原理Fig.2 The principle of MAGM

方法详细步骤如下：

Step1 初始化各合成器的权值。

Step2 一级合成器根据前一积分段的权值进行加权合成。

Step3 二级合成器根据前一积分段的权值进行加权合成。

Step4 将总合成信号反馈到各级合成器。

Step5 一级合成器根据总合成信号进行权值计算、加权合成。

Step6 二级合成器根据总合成信号，对一级合成器的合成信号进行权值计算、加权合成。

重复Step 2～6，可持续进行信号合成。在CPU-GPU异构系统上的计算流程如图3所示。

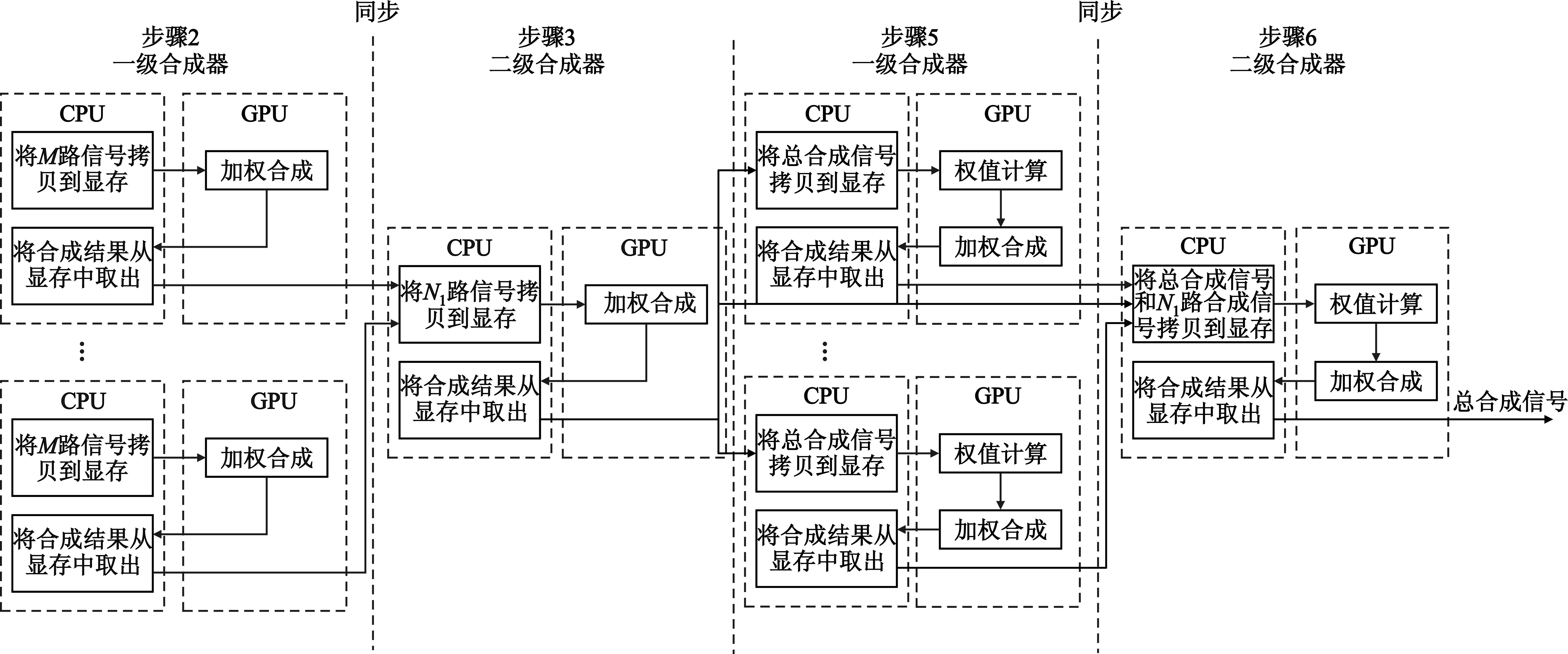
图3 MAGM的计算流程Fig.3 Processing flow of MAGM

下面从单个合成器和MAGM两方面进行实时性分析。

(1)单个合成器的实时性分析

设单个合成器能够处理M路信号，那么满足以下实时性条件：数据传输时间与处理时间之和小于积分时间，即

(5)

式中:D1=ML是数据传输总量，D2=ML是运算量，L是积分段点数，B是传输带宽，P是GPU的双精度浮点性能。把具体数值代入求得M<102.4，即单个合成器最多能实现102路信号实时合成。实际情况要远远糟糕，PCI-e不会达到理论传输速度，算法不能完全并行化，GPU也不会达到计算峰值。

(2)MAGM的实时性分析

若MAGM只有两级合成器，即一级合成器数量是N1，二级合成器数量是1，那么能够处理最多M×N1路天线信号。如果增加三级合成器，二级合成数量是N2，那么能够处理最多M2×N2路信号。为了方便，下面只分析到二级合成器。

对于500个天线的合成问题，显然有

M×N1=500 。

(6)

MAGM能够满足实时性，必须在积分段时长内完成Step 2～6的处理，即

(7)

式中：Ttotal是完成Step 2～6的时间，

Ttotal=max{T2(1),…,T2(N1)}+T3+

max{T5(1),…,T5(N1)}+T6。

(8)

式中：T的下标表示步骤序号，如T2(N1)是Step 2中第N1个一级合成器的处理时间。由于Step 3要等待Step 2的所有一级合成器完成处理，Step 6要等待Step 5的所有一级合成器完成处理，因此Step 2和Step 5的处理时间是所有一级合成器处理时间的最大值。但为了方便分析Ttotal，本文假设Step 2和Step 5中所有一级合成器的处理时间相等：

(9)

那么，式(8)可以简化为

Ttotal=T2+T3+T5+T6。

(10)

每一个T由两部分组成，一是内存和GPU显存之间的数据拷贝时间Ttran，二是GPU计算时间Tpro。显然，Ttotal也由这两部分组成，记为Ttotal,tran和Ttotal,pro：

Ttotal=Ttotal,tran+Ttotal,pro。

(11)

Step 2～6中由CPU拷贝到GPU的数据总量D1是

D1=(M+1)L+(N1+1)L+2L+(N1+1)L=

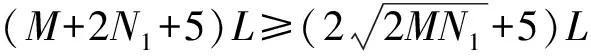
(12)

把式(6)代入式(12)得到

D1≥68.2L。

(13)

对于这些数据量，当PCI-e速度达到理论峰值时，所需传输时间是Ttotal,tran=6.4 ms，远远超过了积分段时间1 ms。可见，在MAGM中，CPU与GPU之间有大量、频繁的数据传输。在本文假设条件下，仅仅数据传输时间就远远超过积分段时间，无法达到实时性要求。因此，MAGM不适用于CPU-GPU异构系统。

3.2 多信号块合成方法

MSBM将高速数字信号按时间先后顺序分流到多个合成器上，每个合成器负责一个积分段的所有天线的合成处理，图4所示为其基本原理，其中，A(i,j)表示第i个天线的第j个积分段。各天线将采样信号送入信号池中，信号池将同一个积分时间段内的信号打包送至任务空闲的合成器中。对单个合成器而言，由于接收到了所有天线的信号，所以合成器不需要总合成信号的反馈辅助。

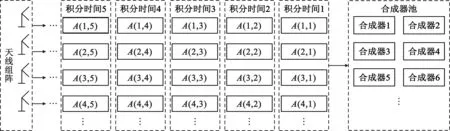
图4 MSBM原理Fig.4 The principle of MSBM

其详细步骤如下：

Step1 初始化合成器的权值。

Step2 接收积分段。

Step3 权值计算，加权合成。

下面对MSBM的实时性进行分析。一个积分段的处理时间Ttotal包含两部分，一是传输时间，将所有天线的信号从信号池传输到合成器所耗费时间；二是计算时间。对于任意的Ttotal，只要合成器数量N0满足式(14)即可保证实时性：

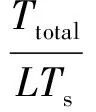
(14)

式(14)的物理意义如图5所示，合成器1从积分段①的起始时刻开始接收信号，然后处理。合成器2在积分段②到来之前保持空闲，从积分段②的起始时刻开始接收信号，然后处理。合成器1处理完积分段①后，保持空闲，直到积分段③的起始时刻。同理，合成器2处理完积分段②后，保持空闲，直到积分段④的起始时刻。如此循环往复，两个合成器轮流对信号进行合成，能够满足实时性要求。

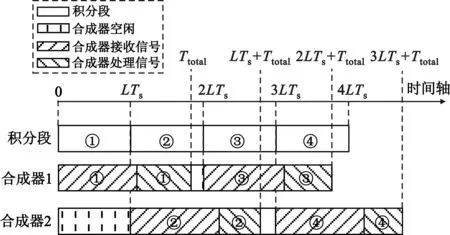
图5 公式(11)的物理意义Fig.5 The physical meaning of Formula (11)

当Ttotal增大时，可以通过增加合成器的数量以保持处理的实时性，具有两点好处：一是可以降低合成器的接收速率，减少单个合成器的带宽需求；二是可以降低合成器的处理速率，减少单个合成器的计算速度需求。

理论上通过增加合成器的数量就可以无限提高方法的处理能力。以本节假设为例，500个天线的积分段时长是1 ms，信号总量是7.5×107Byte，在 16 GByte/s速率下，需要4.7 ms传输时间。对500个天线做相关处理，需要5×107次乘加运算，假如在TESLA K80 GPU上运行并且能完全利用其浮点性能，也至少需要0.02 ms。因此，理论情况下1 ms的积分段需要4.72 ms处理时间，5个合成器即可达到实时处理。

3.3 SUMPLE算法的积分段内迭代方法

MSBM要求各积分段能够并行处理，而常用的SUMPLE算法采用积分段间迭代方法，导致各积分段间存在明显的依赖关系。本文研究了积分段内的迭代方法，其流程如图6所示。在积分段的处理中，各天线权值的初值为0相位，按式(3)进行递推，求得各天线权值的更新值；根据更新值进行加权合成，估计得到合成信号的SNR，当相邻两次合成SNR的变化量ΔSNR小于一定值时停止迭代，否则继续迭代。设停止迭代时的迭代次数是Niter，这种积分段内迭代方法的运算量为NiterNantL。

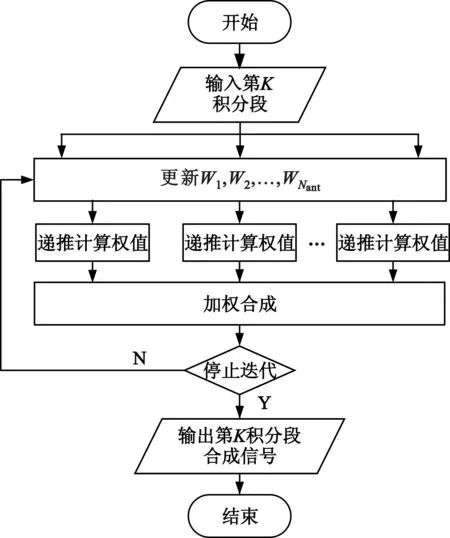
图6 SUMPLE算法的积分段内迭代方法Fig.6 Iterative method inside the integral time interval

4 仿真分析

本文研究积分段内迭代方法的目的是为了对SUMPLE算法进行改造，使不同积分段的处理相互独立，以适用于MSBM方法。只要积分段内迭代方法的性能与积分段间迭代方法的性能相当，就达到预期。对SUMPLE算法的积分段内迭代方法和积分段间迭代方法进行仿真，参数如下：天线数量为20；迭代次数为15；积分长度为100 000；SNR为-15 dB、-10 dB和0 dB；信号形式为单点频信号，频率为1 MHz；采样率为4 MHz。进行500次蒙特卡洛仿真，得到如图7所示的结果。

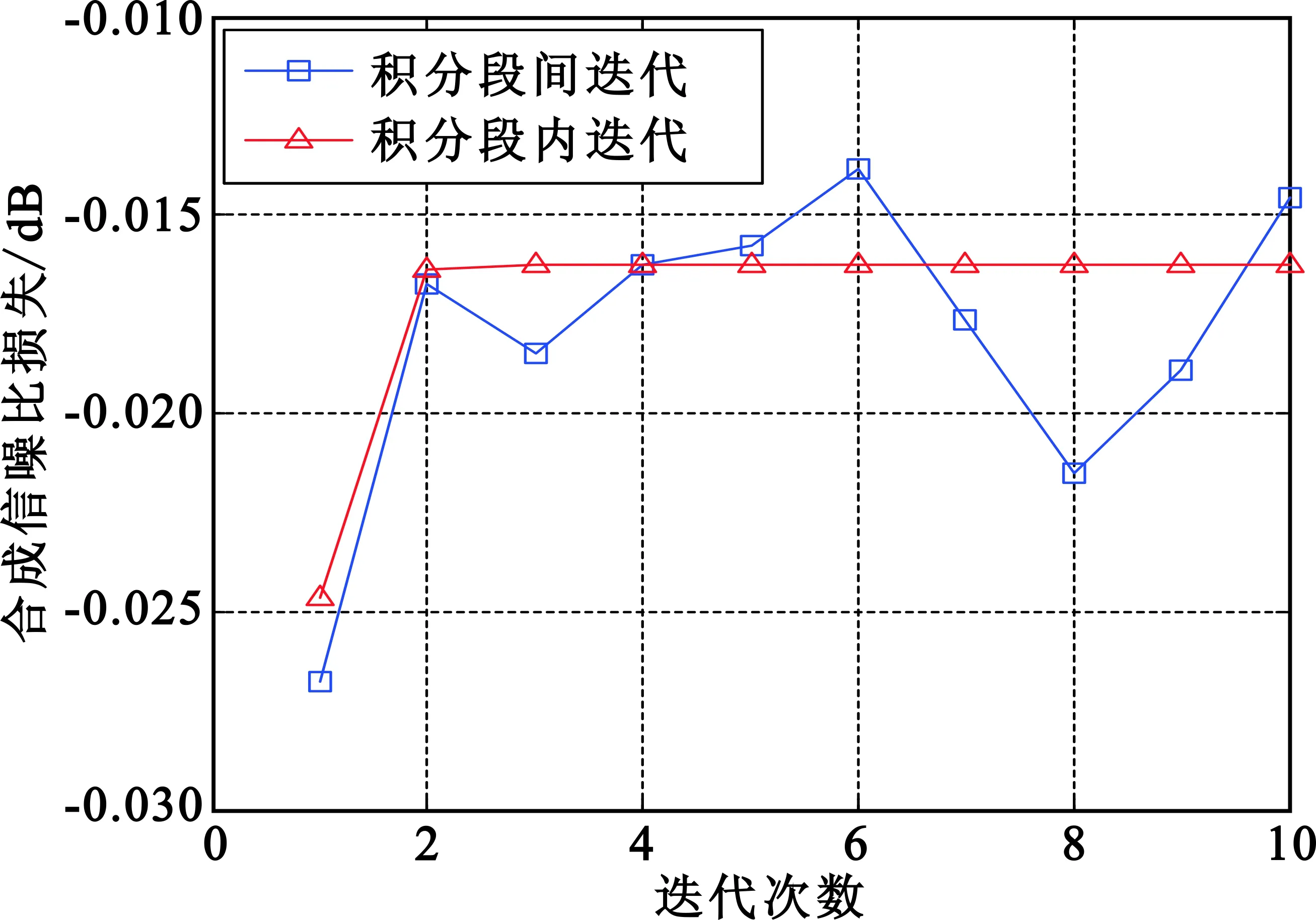
(a)SNR=0 dB

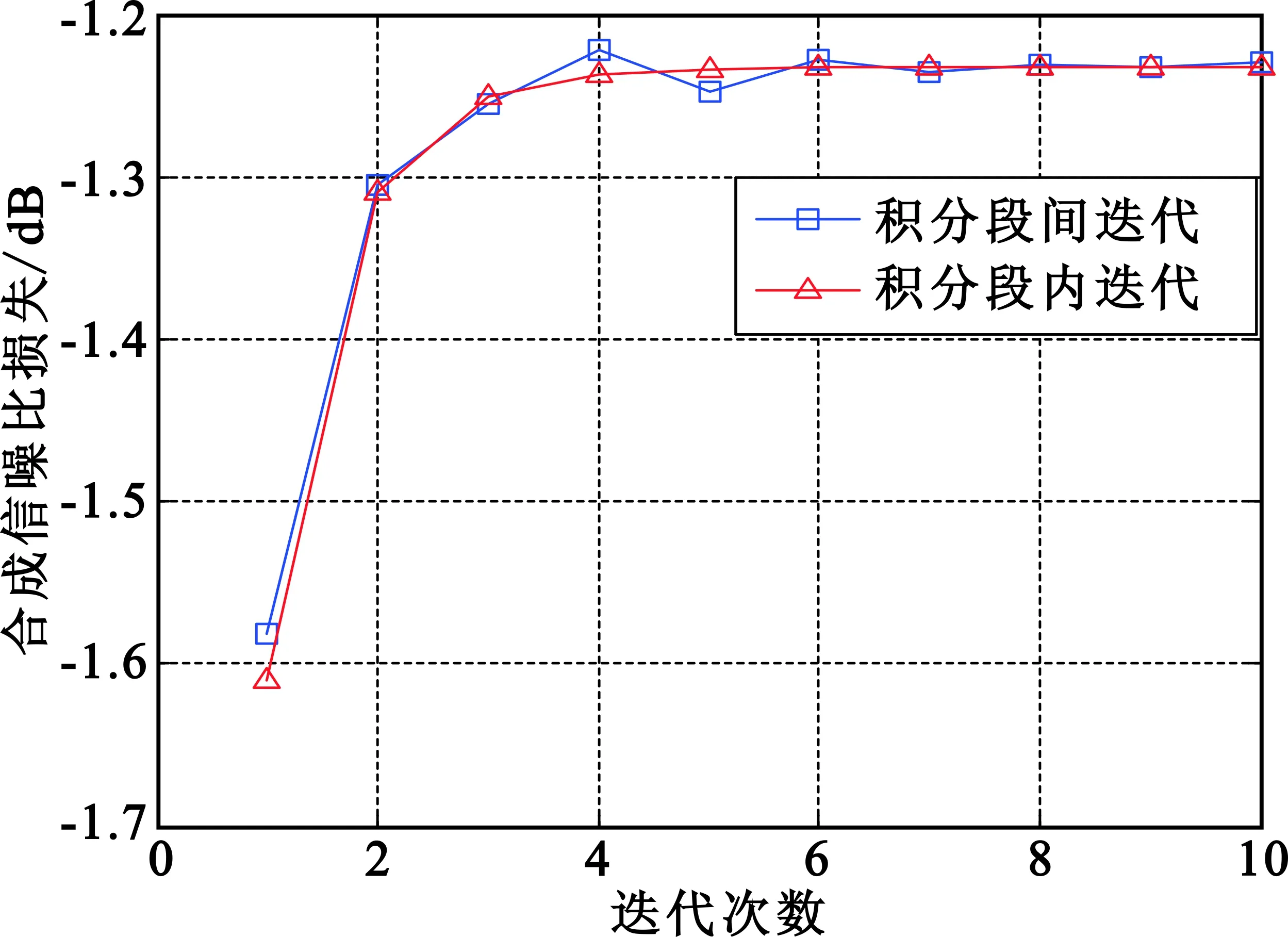
(b)SNR=-10 dB

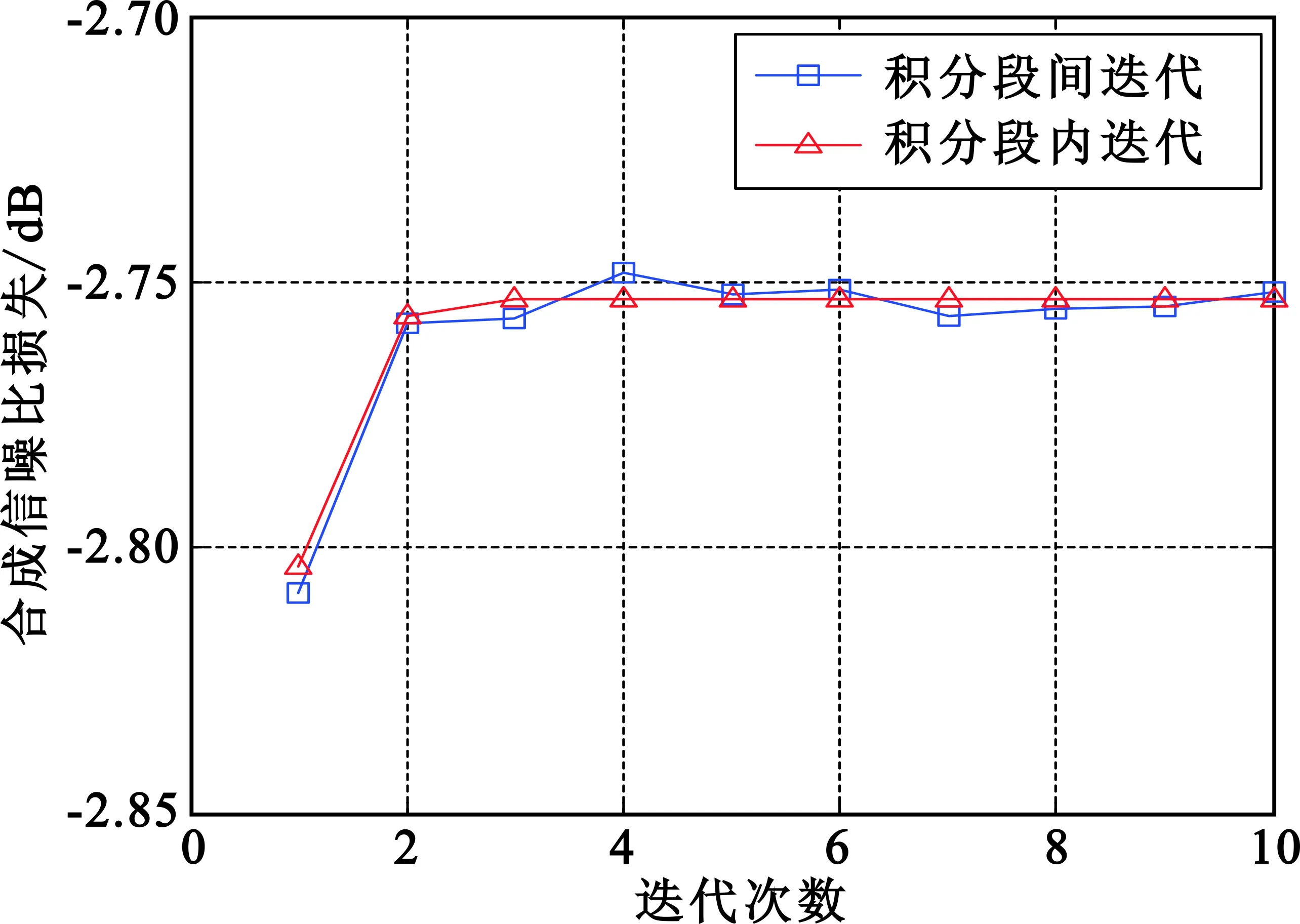
(c)SNR=-15 dB图7 两种迭代方法的合成性能仿真结果Fig.7 Combining performance simulation results of two iterative methods

由仿真结果可得，在3种信噪比下，两种迭代方法的收敛过程和收敛后的合成性能是基本一致的,这已经达到了预期要求，可以将积分段内迭代方法应用到MSBM中，而不带来额外的合成损失。此外，段内迭代方法的抖动要小，对其原因进行分析如下：段内迭代方法是在一个积分段内多次迭代，不断提高权值估计精度，所以合成损失随迭代过程越来越小。段间迭代方法的每次迭代对应不同的积分段，对于每个积分段，只进行了一次权值计算，精度要低于段内迭代方法，即使迭代收敛之后，每次迭代的权值计算精度不尽相同，引起的合成损失也不一样，所以合成损失随迭代过程抖动较大。

5 结束语

本文围绕通用计算平台上的大规模天线组阵合成方法展开研究，对MAGM和MSBM的实时性进行分析，结论是：MAGM需要大量频繁数据通信，不适用于通用计算平台；MSBM通过增加合成器数量，降低合成器的通信带宽和处理速度需求，具有很大的处理能力提升空间，且适用于通用计算平台。研究了SUMPLE算法的积分段内迭代方法，其与积分段间迭代方法具有相同的合成性能。本文研究结果对在通用计算平台上进行大规模天线组阵信号合成具有一定的指导意义。下一步将结合具体CPU-GPU平台进行实现验证。