依据信噪比的雷达信号质量估计

(空军航空大学 航空作战勤务学院,长春 130022)

1 引 言

在战场电磁环境中，微弱信号由于其功率低，甚至达不到接收机灵敏度，尤其是低截获概率(Low Probability of Intercept,LPI)雷达采用功率管理技术，致使现有技术无法对此类信号实现有效处理。信号增强技术是专门针对微弱信号侦察截获难而进行的研究，其中如何检验增强技术是否有效是信号增强的重要部分，最直接的方法是对比增强前后信号质量。在具体的验证中，本文通过对比信号的信噪比来衡量信号的质量。

信噪比(Signal-to-Noise Ratio,SNR)一直是现代通信系统中一个非常重要的参数，在传统电子战领域研究得不多。许多学者在通信领域就信噪比估计这一问题进行了广泛研究。文献[1]研究了针对线性调频信号在时间域上利用傅里叶级数拟合自相关主瓣达到信噪比估计的算法，主要分析了时宽和带宽对结果的影响。文献[2]为在载波频率精确恢复前提高多进制数字相位调制信号在低信噪比下的估计精度，提出了一种在符号定时恢复和帧同步后提取同步段符号，相关运算后在频域进行信噪比估计的算法。文献[3]研究了利用最大似然估计法解决在调频差分混沌键控系统中的多径瑞利衰落信道的信噪比估计问题。文献[4]将Gram-Schmidt正交化过程引入到紧缩投影近似子空间跟踪(Projection Approximation Subspace Tracking deflation,PASTd)中，使计算得到的特征向量相互正交，从而保证算法具有更好的收敛性能。文献[5]研究了在高动态环境下基于数据辅助信噪比估计算法，其实质是利用似然函数求微分的思想。

本文根据雷达信号复杂多变的特点，采用基于子空间分解的信噪比估计算法：首先针对传统算法对自相关矩阵估计不准的问题进行改进，随后利用粒子群优化(Partical Swarm Optimization,PSO)算法[6]对自相关矩阵进行特征值分解，然后利用最小描述长度(Minimum Description Length,MDL)算法[7]确定出信号的维数，将信号分为信号子空间和噪声子空间，进而实现信噪比估计。本文在加性高斯白噪声(Additive White Gaussian Noise，AWGN)信道条件下进行理论推导和仿真讨论，从标准偏差和方差的角度估计信噪比估计算法的性能。

2 信号模型

任何信号都可以表示为各种谐波之和，因此，任何信号估计问题都可以等效为谐波估计问题。在本文中假设信号模型如下：

(1)

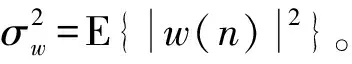
3 信噪比估计计算

信号x(n)可以变形为

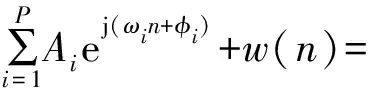
(2)

式中：αi=Aiejφi。

取时间长度为M的时间窗，窗内的信号{x(n),n=n,n+1,…,n+M-1}可以表示为矢量的形式：

X(n)=[x(n),x(n+1),…,x(n+M-1)]T。

因此，

(3)

式中：

w(n)=[w(n),w(n+1),…,w(n+M-1)]T，
V(fi)=[1,ej2πfi,…,ej2π(M-1)fi]T。

X(n)的自相关矩阵为

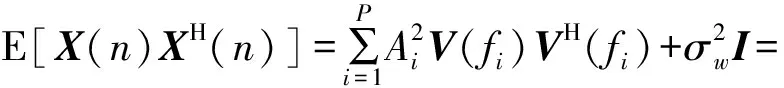
(4)

式中：

V=[V(f1),V(f2),…,V(fP)]M×P，

自相关矩阵RX可以表示为

(5)

式中：λm是以降阶排列的RX的特征值，λ1≥λ2≥…≥λM；qm是相应的特征向量，而

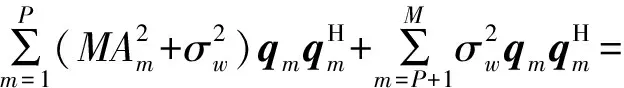
(6)

式中：

Qs=[q1,q2,…,qP]M×P,

Qw=[qP+1,qP+2,…,qM]M×(M-P)。

在整个分析问题过程中，关键是要能够确定Λ的秩P，就能通过自相关矩阵RX的特征值分解实现区分开信号子空间和噪声子空间，由此信噪比估计值可以由以下公式计算：

(7)

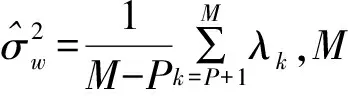
3.1 自相关矩阵估计改进

在进行信噪比估计的过程中，如果采用式(4)计算出来的结果作为信号自相关矩阵，就会存在一定的偏差。

真实情况下X(n)的自相关矩阵为

RX=E[X(n)XH(n)]=

E[(S(n)+w(n))(S(n)+w(n))H]=

Rss+Rww+Rsw+Rws。

(8)

比较式(8)和式(4)，式(8)的前两部分是式(4)中的两项和，代表了信号和噪声部分；后两部分代表了信号和噪声的互相关。在研究的模型当中，假定的噪声是零均值并且和信号是不相关的，因此式(4)中后两部分应该等于零。然而，在数据量有限的情况下，式(8)中后两项就会变得重要，它直接导致了自相关矩阵估计偏离真实值。

本文就针对上述问题在估计自相关矩阵时提出了改进形式。改进的信号矩阵形式为

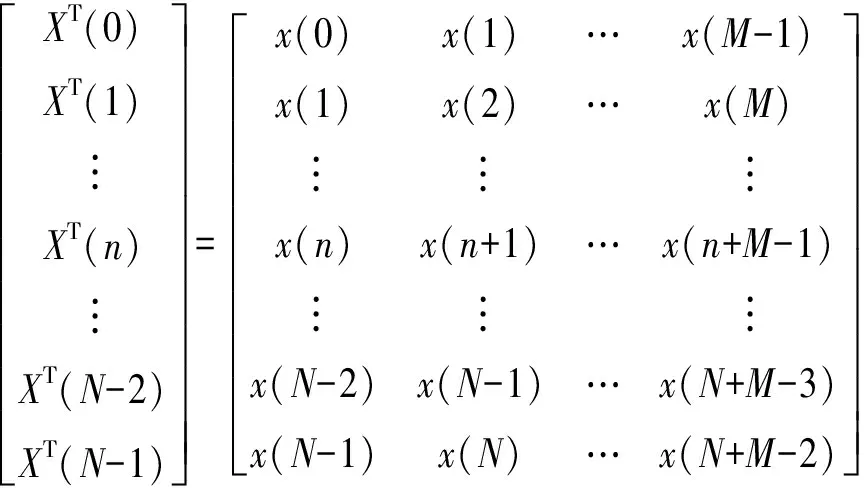
(9)

式中：n=0,1,…,N-1，N是信号的长度，又叫快拍数。

这样改进的目的是充分考虑到信号和噪声之间的相关性，尽可能按照式(8)来构造信号矩阵，相对于式(4)提高了估计精度。改进后的信号自相关矩阵为

(10)

3.2 特征值计算

信号自相关矩阵的特征值计算是本文的一个重要组成部分，准确快速地对自相关矩阵RX进行特征值分解是基于子空间理论进行信噪比估计的关键。普通的求解方法有迭代法和变换法，其中，迭代法是利用矩阵向量之间相乘进而求得特征值和特征向量，常用的方法有Lanczos法[8]、Davidson法[9]等；变换法则是直接对矩阵进行变换，使之变成容易求解特征值和特征向量的新矩阵。这些方法都是矩阵论中的经典计算方法，但是普遍存在着存储量大、精度低、收敛速度较慢等不足。另外可以采用一些分解矩阵的方法，例如Jacobi旋转[10]和QR分解[11]，但其都存在计算量大、收敛速度慢的缺点。粒子群优化算法是基于群体智能的进化优化算法，采用实数求解，需要调整的参数较少，且算法简单,易于实现。因此，本文选其作为RX矩阵特征值求解的方法。

3.2.1PSO算法

PSO初始化开始时，会随机产生一群粒子又叫做随机解，在这个过程中粒子不断跟踪两个极值，一个是个体极值，指的是粒子自身找到的最优位置；另一个是全局极值，指的是迄今整个粒子群找到的最优位置来更新速度和位置。

假设第i个粒子的位置是Xi=(xi1,xi2,…,xid)，速度是Vi=(vi1,vi2,…,vid)，其中d是粒子的维数；第i个粒子的历史最优位置为Pi=(pi1,pi2,…,pid)，其适应度值记为fitness(Pi)；迄今为止粒子群搜索到的最好位置记为Pg=(pg1,pg2,…,pgd)，其适应度记为fitness(Pg)。粒子按照下式调整自己的位置：

(11)

(12)

式中：1≤i≤N，N为粒子群规模；1≤d≤D，D为粒子维数；k为迭代次数(k≥0)；加速常数c1和c2是非负数；r1和r2是(0,1)区间的随机数；惯性权重w一般取0.5～0.9之间的常数。在解空间内粒子不断跟踪个体极值与全局极值进行搜索，直到达到规定的迭代次数或者满足规定的误差标准为止。

3.2.2基于PSO的特征值求解

个体由粒子位置X和粒子速度V这两部分组成，分别包含两个分量，即(X,V)=((x1,x2),(v1,v2))，其中，(x1,x2)对应矩阵特征值的实部和虚部，即特征值λ=x1+x2i；(v1,v2)表示特征值对应的速度的实部和虚部。

把个体代入特征方程P(λ)=|A-λI|=0中，得P(λ)=A-(x1+x2i)I=0，设e=det(A-(x1+x2i)I)，对λ的求解转化为e=det(A-(x1+x2i)I)的最小化问题。即PSO的适应度函数为

minf=|det(A-(x1+x2i)I)| 。

(13)

基于PSO的矩阵特征值求解步骤如图1所示。

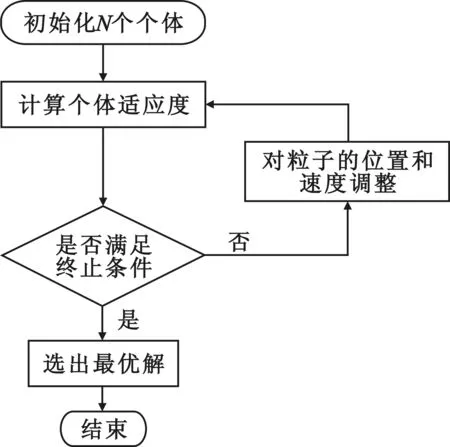
图1 PSO算法求解矩阵特征值流程 Fig.1 PSO algorithm process for solving matrix eigenvalue

3.2.3PSO的改进

为了防止PSO算法进入局部最优值“陷阱”，缩短算法收敛时间，本文对PSO算法进行如下改进：

(1)如果粒子的适应度值不等于fitness(Pg)，利用式(11)、(12)更新其位置；

(2)如果粒子的适应度值等于fitness(Pg)，利用如下公式更新其位置：

4 信号子空间维数的确定

含有噪声的信号的维数可以由最终预测误差(Final Prediction Error,FPE)[12]、赤池信息量(Akaike Information Criterion,AIC)准则、自回归传递函数或者最小描述长度来计算，但是在接收雷达信号较少的情况下，最小描述长度效果最好[13]。所以，本文选择MDL原理来计算信号子空间的维数:

(14)

则信号子空间的维数为

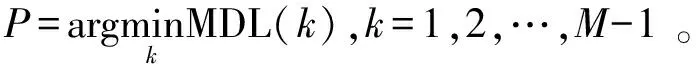
(15)

综上理论分析，得出信噪比估计的过程如下：

(1)建立雷达信号的自相关矩阵RX；

(2)利用PSO算法对RX进行特征值求解，求出其特征值序列；

(3)依据MDL原理表达式确定RX的维数P；

(4)按照式(7)求其信噪比估计值。

5 仿真与性能分析

为了测试算法的性能，我们选取雷达信号中最常见的常规雷达信号、线性调频信号(Linear Frequency Modulation,LFM)和二相编码信号(Binary Phase Shift Keying,BPSK)并进行100次蒙特卡洛(Monte-Carlo)仿真实验，主要分析观测长度M和不同信号对实验结果的影响。在仿真实验中，采用信噪比的估计均值和估计均方根误差(Root Mean Square Error,RMSE)来衡量算法的性能。RMSE定义如下：

5.1 仿真1

设置情景:接收机收到一个常规雷达信号，信号形式为单一载频。信号长度为256点，时间窗长度为16，初始种群个数为50，惯性权重为0.8，空间维数为2，两个加速常数都为0.5。在本实验中，设置信号的归一化频率为0.03。仿真结果如图2所示。

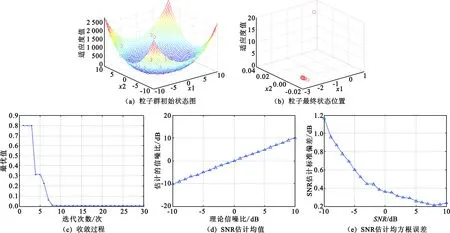
图2 一部常规雷达信号SNR估计Fig.2 SNR estimation of a conventional radar signal

5.2 仿真2

设置情景:接收机收到两部常规雷达信号，信号形式均为单一载频。在本实验中，设置两个信号的归一化频率分别为0.03和0.07。仿真结果如图3所示。

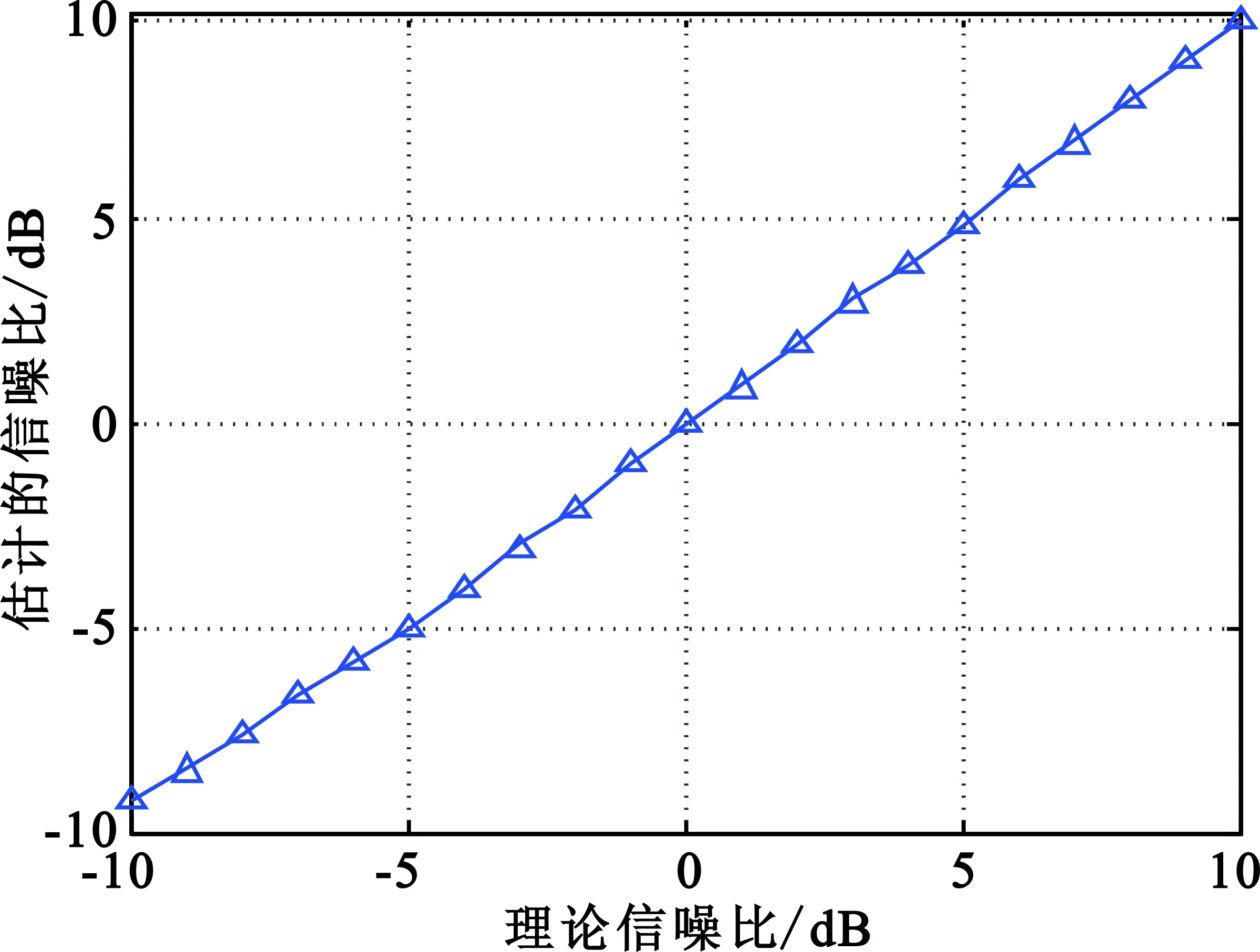
(a)SNR估计均值

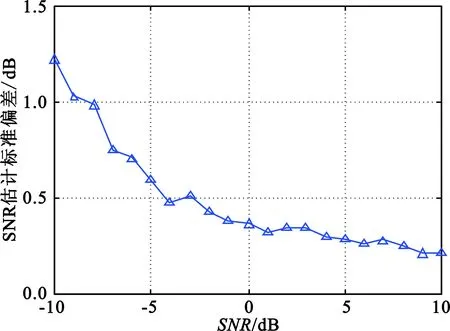
(b)SNR估计均方根误差图3 两部常规雷达信号SNR估计Fig.3 SNR estimation of two conventional radar signals

5.3 仿真3

设置情景:接雷收机收到两部达信号，其中一部为常规雷达信号，信号形式为单一载频，归一化频率值为0.03；另外一部为低截获概率雷达，采用线性调频的调制方式，归一化频率变化范围0.01～0.02。仿真结果如图4所示。

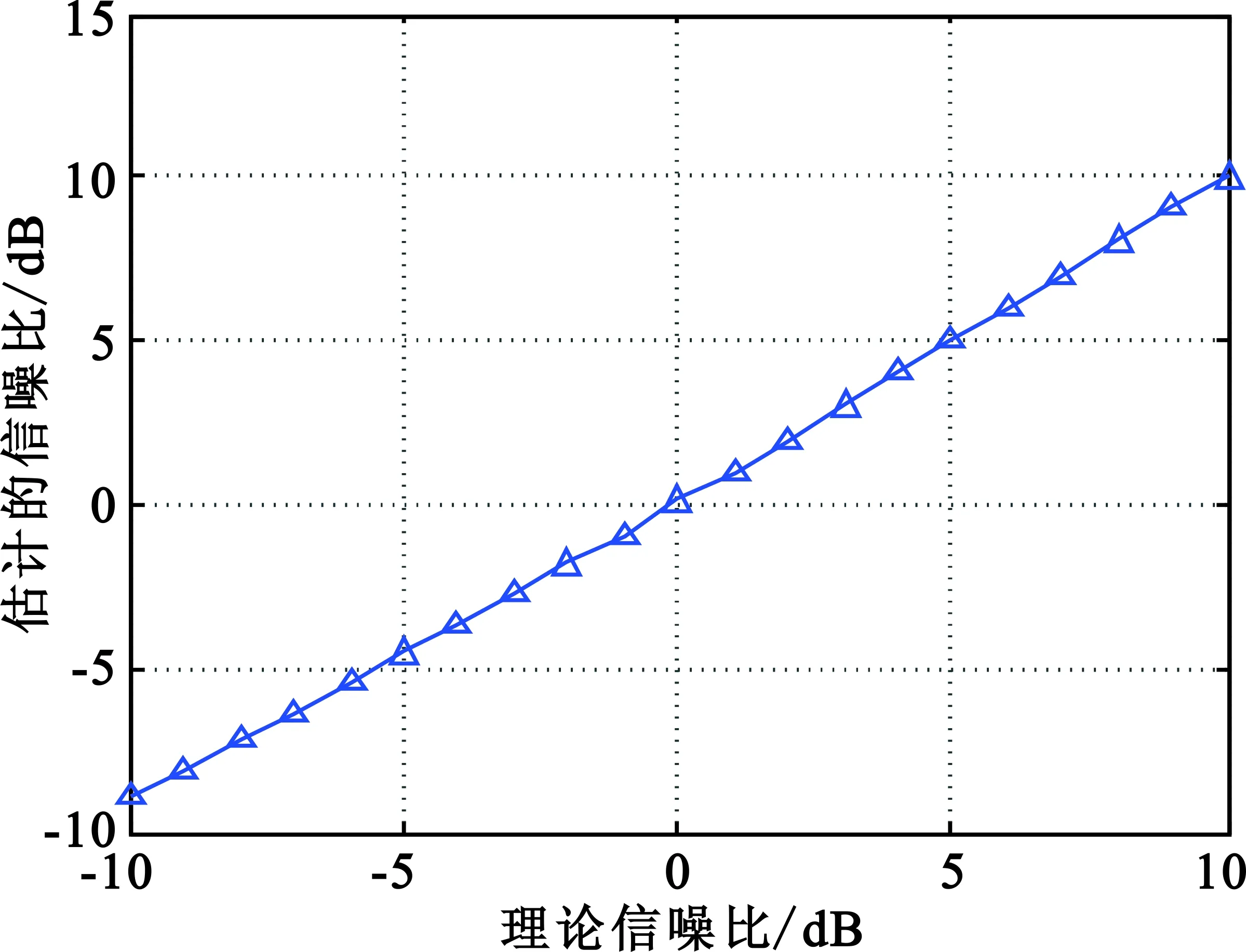
(a)SNR估计均值

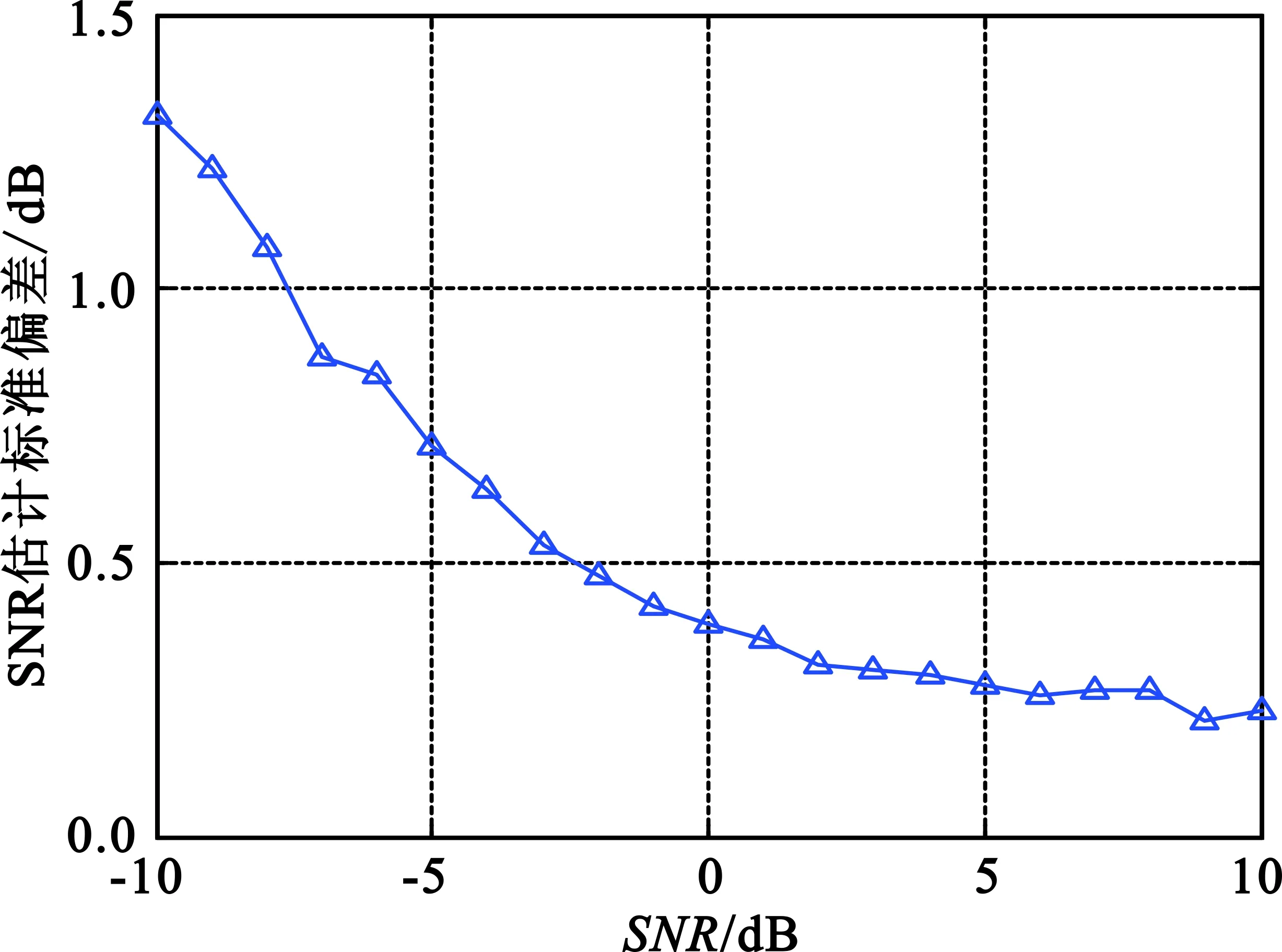
(b)SNR估计均方根误差图4 常规和线性调频样式混合信号SNR估计Fig.4 The conventional and LFM mixed signal SNR estimation

5.4 仿真4

设置情景:接收机收到3部雷达信号，其中一部为常规雷达信号，信号形式为单一载频，归一化频率值为0.03；另外一部为低截获概率雷达，信号采用线性调频的调制样式，归一化频率变化范围0.01～0.02；第三部也为低截获概率雷达，信号采用二相编码的调制样式，归一化频率为0.025。仿真结果如图5所示。

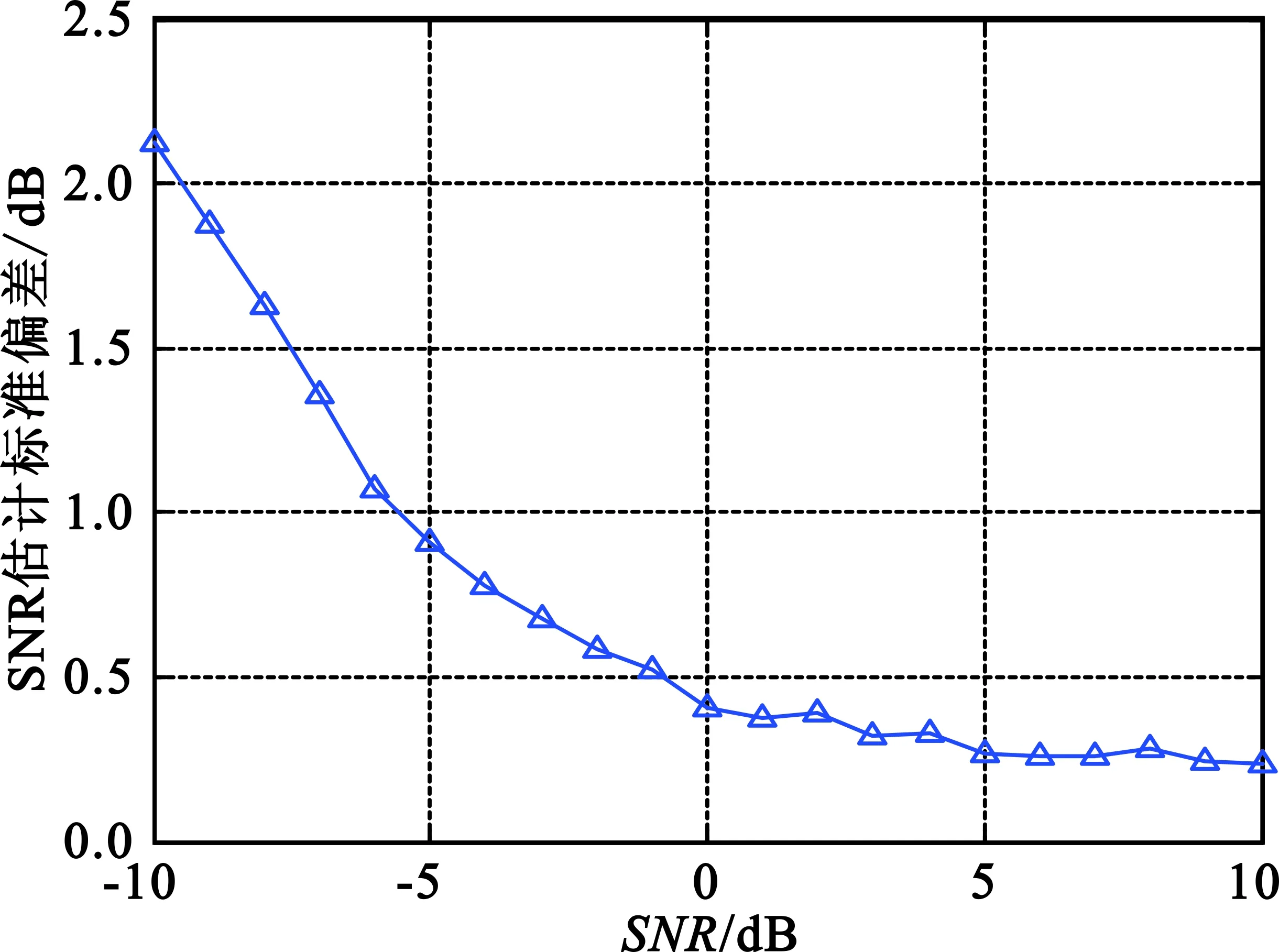
(b)SNR估计均方根误差

5.5 仿真5

将本文的算法和EB方法、GT方法和M2M4方法[14-16]进行性能对比，设置信号和仿真1的相同。仿真结果如图6所示。

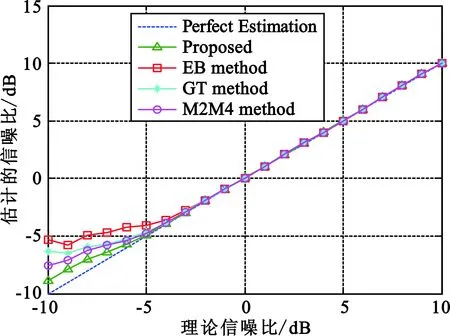
(a)不同方法的SNR估计均值

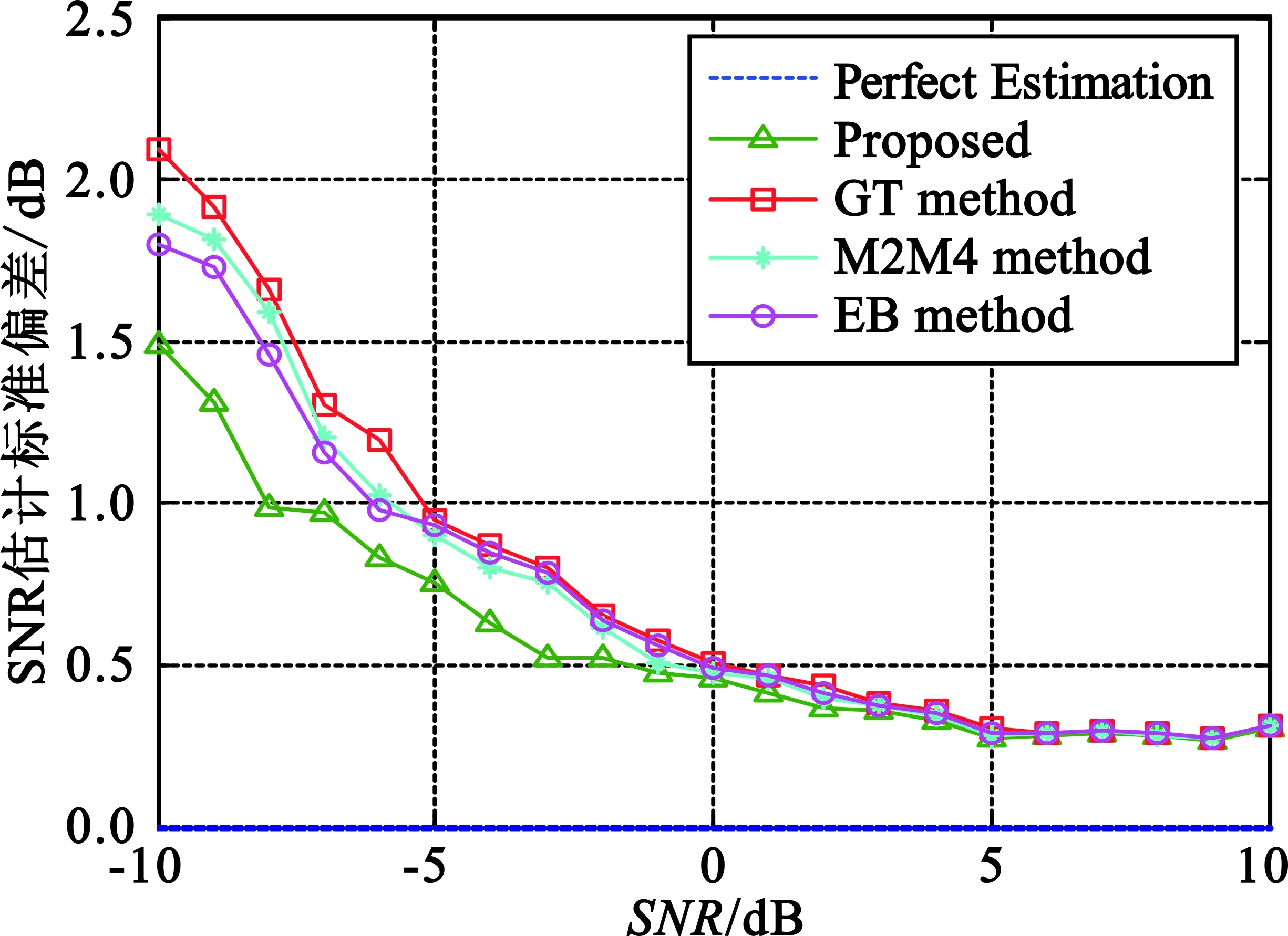
(b)SNR估计均方根误差图6 4种方法的SNR估计Fig.6 SNR estimation comparison among four methods

仿真1～4分别设置了不同的信号条件，从单一常规信号一直增加到多个复杂调制信号混叠输入，从结果来看，经过100次的蒙特卡洛实验，在-10～10 dB之间信噪比估计值与理论值基本相等，随着SNR逐渐增大，估计的均方根误差呈现指数衰减，属于正常误差范围之内。仿真5将本文算法同文献[14-16]的信噪比估计算法进行了性能对比，从仿真结果来看，当SNR<-3 dB时，本文算法的估计值精度优于其他算法，均方根误差明显小于其他算法。此外，在求解自相关矩阵的特征值时，本文运算复杂度为O(n2)，而基于QR分解的算法复杂度为O(n3)。

6 结 论

本文研究了在复杂电磁环境中对接收雷达信号的信噪比估计，解决了在有限信号量下自相关矩阵估计偏差问题，同时也解决了传统算法求解特征值复杂度高、运算速度慢的问题。仿真结果表明，本文算法明显优于EB方法、GT方法和M2M4方法，有效提高了估计精度。此算法是一种进行盲信噪比估计的有效方法，实现了将信噪比作为衡量信号质量的指标，为信号增强研究领域提供了准确有效的检验方法。在后续研究中，我们将考虑在更低信噪比的极端环境下的算法改进。