基于噪声分布特性的脉冲信号自适应门限检测

(中国西南电子技术研究所，成都610036)

1 引 言

信号检测是侦测系统的基础，即在噪声中检测有无信号。信号检测主要包含三方面内容：判决统计量的选取、判决门限的调整和判决算法的确定。自适应门限检测即通过自动计算判决统计量以设置合理的门限，并自动判决信号有无。常见的判决统计量包括时域和频域的统计量，时域统计量为信号能量[1-2]，频域统计量则包括幅度谱[3]、循环谱[4-5]。另外，针对特定信号检测的二阶矩(相关函数)、高阶矩[6]甚至高阶累积量[7-8]也用于判决统计量，但计算复杂度很高，不适合高密度的脉冲信号检测。而时域的信号能量判决和频域的幅度谱判决，需要先检测出一段时间内的信号功率并以此作为当前检测的门限，然后随着时间推移依次滑动，自适应调整检测门限，当大信号比邻小信号时，门限会被拉高，造成漏检。

为降低计算复杂度，并解决传统自适应门限检测方法中大信号比邻小信号时门限被拉高的问题，本文提出一种基于噪声分布特性的自适应门限算法，用于对脉冲信号进行目标检测。

2 信号幅度差分模型

从接收机采集得到的数字脉冲序列可表示为

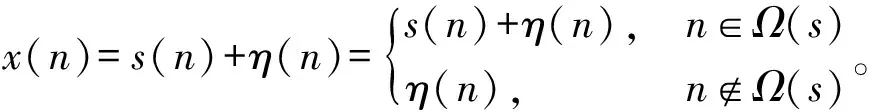
(1)

式中：s(n)表示复信号序列，η(n)表示叠加的噪声，Ω(s)表示存在目标信号的区域。忽略量化噪声因素，η(n)主要源于接收机噪声，服从高斯分布，为了分析方便，可设为均值为0、方差为σ2的加性高斯白噪声(Additive White Gaussian Noise，AWGN)。为了方便讨论，这里假设噪声的频谱无限宽，信号幅度是方波型(其他梯形状与方波型的差别不大)。

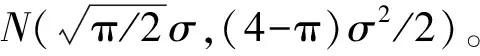
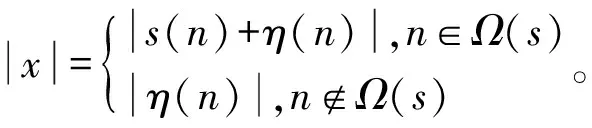
(2)

此处产生两个脉冲信号，信噪比分别为5 dB和2 dB，信号的实部时域波形和幅度分别如图1和图2所示。

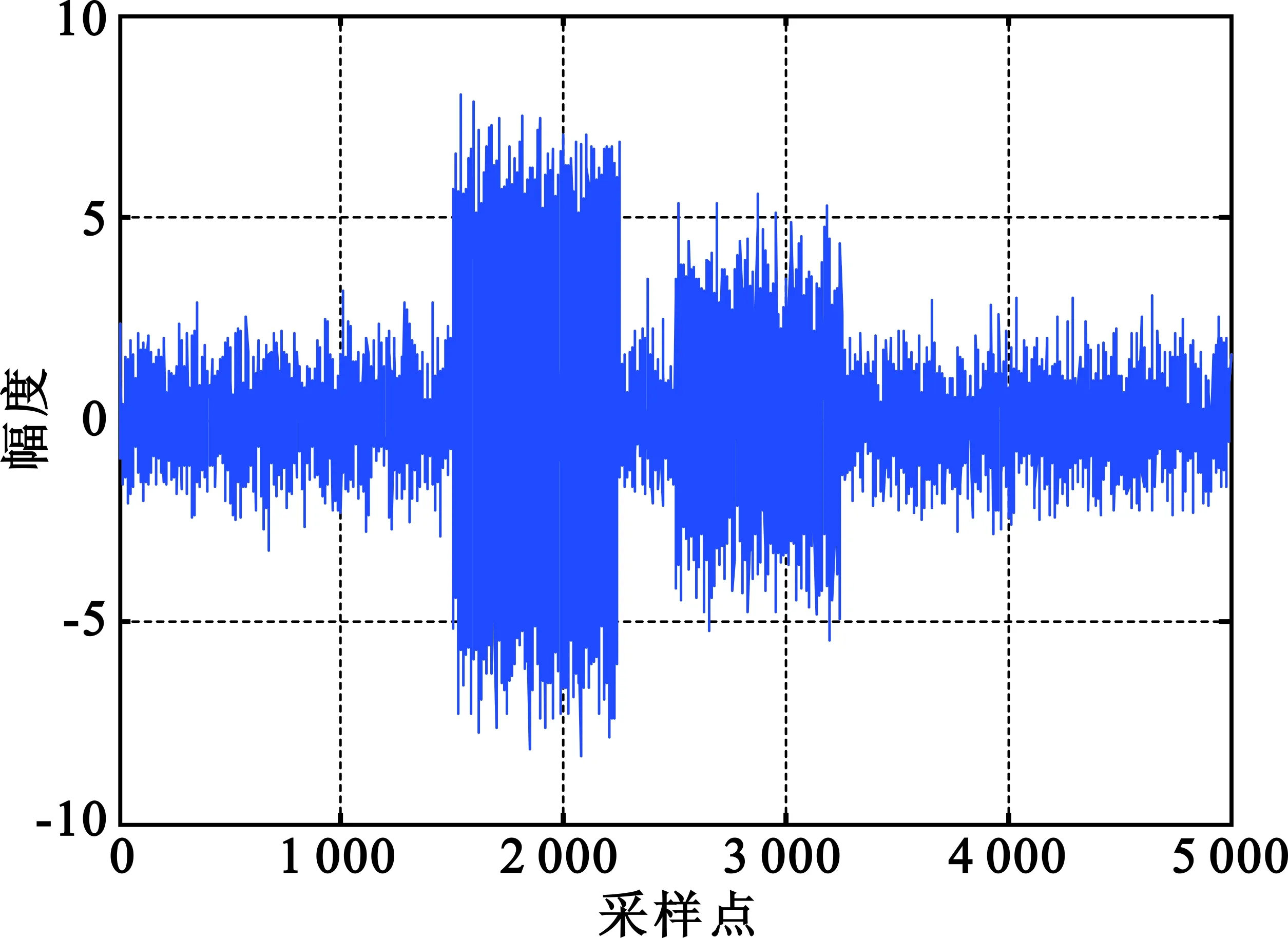
图1 信号实部波形Fig.1 Waveform of the real part

图2 信号幅度Fig.2 Signal amplitude

由于噪声η(n)是叠加在信号s(n)上，故对式(2)做差分可得

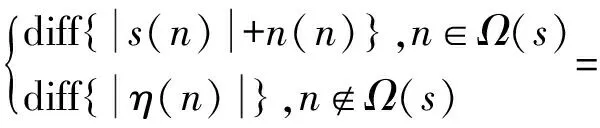
(3)

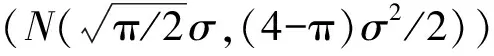
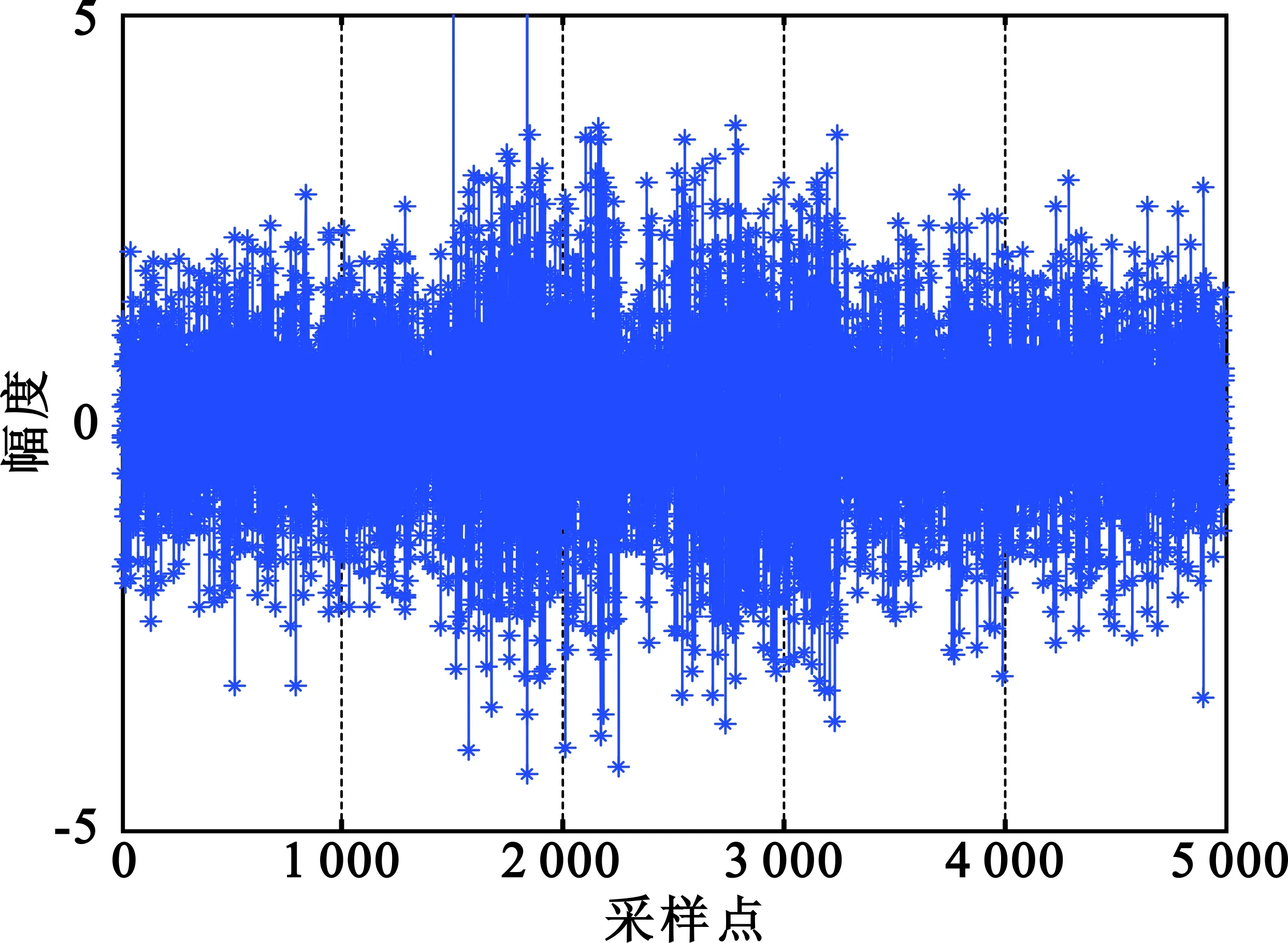
图3 信号幅度的差分Fig.3 Difference of signal amplitude

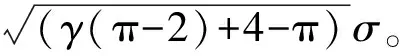
3 基于方差的自适应门限

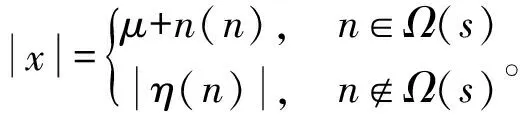
(4)

这里假设信号能量大于噪声能量，不然无法从时域检测出信号。则当门限为τ时，发生区分错误的概率为

(5)

这里忽略掉第二项概率密度函数小于0部分(事实上这部分很小，可以忽略)。由假设条件和瑞利高斯概率密度函数单峰性可知必有最小的P值存在，同时概率密度函数的连续性，保证了P可导性，因此当P对τ的偏导数为0时必然对应P的最小值。令

(6)

设τ=mσ,μ=kσ，则上式可进一步化简为

(7)

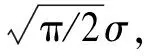
由于门限的设置是为了能检测幅度较低的信号，而幅度很大的信号则不是关注重点，因此这里假设信号幅度小于噪声均方差k0倍，则式(7)右边满足

(8)

再根据幂指数展开近似要求，将式(7)右边改写为泰勒级数展开形式，即

(9)

即将式(7)转化为代数方程，可以根据不同环境要求k0得到门限τ的比值m。

e(mk-k2/2)≤ek2/2≤eπ，

(10)

(11)

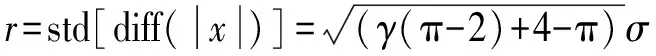
(12)

由于占空比γ满足0≤γ≤1，故由式(12)可得门限τ的范围为1.322 2r≤τ≤2.018r。

4 基于均值的自适应门限

(13)

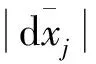
(14)

由于两变量分布不完全相同，差分后概率密度函数必然关于Y轴对称，故只需考虑正半轴的概率密度函数，即

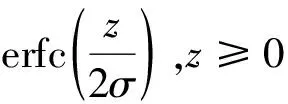
(15)

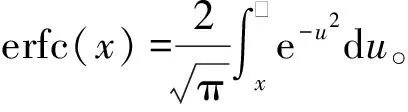
综合式(14)和式(15)可得

(16)

这里只给出正半轴部分的表达式。

(17)

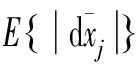
(18)

设占空比为γ，综合n∉Ω(s)和n∈Ω(s)有

(19)

将τ=1.869 6σ代入式(19)可得

(20)

由于信号幅度的差分与信号幅度的关系不大，可以将γ设为0，计算门限τ。由式(20)可知，计算门限τ仅需计算幅度差分后的均值，并乘以一个常数，仅涉及到简单的加法和乘法运算，计算复杂度低。

综上可得，计算数字脉冲信号自适应门限的算法步骤如下：

Step1 计算信号幅度|x(n)|。

Step5 根据式(20)计算门限τ。

5 仿真实验

为验证算法的有效性，进行了以下两方面的仿真，一是脉冲信号功率差异不大的情况，二是大信号比邻小信号的情况。仿真使用式(20)计算所得门限与信号幅度之间的关系。

如果不考虑接收机的自动增益控制，在没有外界干扰的实际系统中，接收机的噪声功率是近似恒定不变的，而接收信号的功率则是随着环境的变化在大动态范围内变化，故接收信号的信噪比主要由信号的功率决定。在后续的仿真中保持噪声功率不变，通过调整接收信号的功率来调整信噪比。

5.1 信噪比相同时信号幅度与门限的关系

当信噪比为5 dB时，产生两个脉冲信号，脉冲信号幅度与门限之间的关系如图4所示，其中门限1为传统方法计算所得的门限，门限2为式(20)计算所得门限。

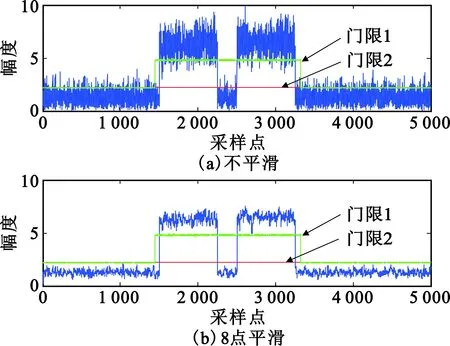
图4 信号幅度与门限之间的关系图Fig.4 Relationship between signal amplitude and threshold

由图4可知，通过式(20)计算所得的门限基本上是紧贴着噪声的，不仅能提高信号检测的概率，相对于使用传统方法计算的自适应门限，还降低了计算量。为了降低虚警和漏检的概率，信号检测时一般需要对信号做平滑处理，故图4还给出了平滑后信号幅度与门限之间的关系。

5.2 大信号比邻小信号时信号幅度与门限的关系

当信噪比分别为5 dB和2 dB时，产生两个脉冲信号，脉冲信号幅度与门限之间的关系如图5所示，其中门限1为传统方法计算所得的门限，门限2为式(20)计算所得门限。

图5 大信号比邻小信号时信号幅度与门限之间的关系图Fig.5 Relationship between signal amplitude and threshold when weak signals are next to strong signals

由图5可知，通过式(20)计算所得的门限没有出现传统方法中大信号比邻小信号时，门限被拉高的情况。

为了验证算法用于信号检测的性能，做1 000次蒙特卡洛实验，并统计检测概率。假设信噪比为-5～5 dB，间隔1 dB，得到检测的概率统计图如图6所示。

图6 信号检测概率与信噪比的关系曲线Fig.6 Relationship between the detection probability and SNR

由图6可知，在不平滑的情况下，通过式(20)计算所得门限在信噪比3 dB时能很好地检测出信号,并且在相同条件下，平滑点数越高，检测性能越好。

6 结 论

计算信号幅度差分绝对值的均值可以得到信号检测的时域判决统计量，仿真实验验证了该算法的有效性。算法解决了大信号比邻弱信号时门限被拉高的问题，且运算复杂度低，非常适合于实时性要求高而资源不足的FPGA硬件平台实现。在实际的信号检测系统中，本文算法已经取得了良好的检测效果，为脉冲信号的实时捕获和后续的侦察处理提供了支撑。对基于频域噪声分布特性的自适应门限的相关算法正在进一步研究中。