异构网络中基于功率控制的能效优化算法
谷 静,刘亚茜,张 新,王倩玉
(西安邮电大学 电子工程学院, 陕西 西安 710121)
0 引 言
近年来,节能减排、降低功耗成为现在通信业的研究热点,近80%的消耗来自于网络中的基站消耗[1,2]。异构网络[3]中低功率节点[4](low power node,LPN)的引入弥补了单一宏蜂窝网络的性能缺陷,但为了更好的区域覆盖,不可避免地需要部署大量LPN,使整个系统功耗增加,引发人们对蜂窝异构网络能效(energy efficiency,EE)[5]的担忧和思考。
在此方面,相关文献进行了大量研究,下面主要从资源分配角度分析异构网络中的能效变化。文献[6]通过凸优化理论得到最优联合子载波和功率分配策略,提出一种求解超越方程组的方法,但此文献中提出的算法计算复杂度较高。文献[7]将宏基站发射功率作为网络能耗最大的部分,采用梯度上升方法控制宏基站发射功率,给出资源分配问题的最优性条件,验证算法的收敛性,但是通过控制宏基站发射功率影响了宏用户的服务质量。文献[8,9]利用遗传算法提高了系统吞吐量等性能。目前在异构网络与遗传算法相结合的文献中大部分从吞吐量等性能进行分析,较少文献利用遗传算法研究异构网络中的能效情况。
在此基础上,提出一种基于功率控制的能效优化算法。在PBS发射功率的限定条件下提出以能效为目标的优化函数并利用遗传算法[10]对多个PBS的发射功率进行控制,在保证用户服务质量前提下,实现能效最大化,减少算法复杂度。同时改进遗传操作使得解集趋于更快、更优的方向收敛。
1 系统模型及干扰分析
异构网络中的LPN包括远程射频头(remote radio head,RRH)、微微基站(PBS)、家庭基站(femto base station,FBS)以及中继(Relay)等[11],以宏基站和微微基站构成的异构网络为研究背景,系统模型及干扰场景如图1所示。
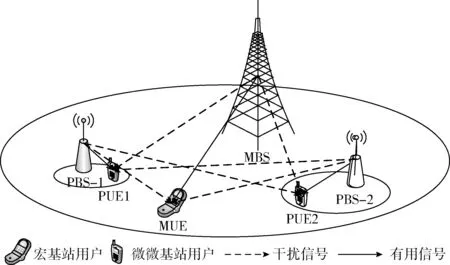
图1 系统模型及干扰分析场景
MBS覆盖区域为蜂窝状正六边形区域,MBS位于正六边形中心位置,PBS均匀分布于MBS边缘区域,每个基站内部随机分布若干用户。为了提高频谱利用率,宏基站(macro base station,MBS)和PBS共享同一段频谱,每个小区包含K个物理资源块(physical resource block,PRB),每个PRB占用带宽为180 kHz,且每个用户分配1个PRB进行通信。
由图知MUE由MBS服务,PUE1由PBS-1服务,PUE2由PBS-2服务,在MBS-PBS两层异构网络中,存在以下3种下行干扰:
(1)MBS对PUE的跨层干扰,如MBS-PUE1,MBS-PUE2;
(2)PBS对MUE的跨层干扰,如PBS-1-MUE,PBS-2-MUE;
(3)PBS对PUE的同层干扰,如PBS-1-PUE2,PBS-2-PUE1。
综上所述,宏基站用户MUE受到来自PBS-1和PBS-2的跨层干扰,而微微基站用户PUE1受到来自MBS的跨层干扰和PBS-2的同层干扰,PUE2受到来自MBS的跨层干扰和PBS-1的同层干扰。
假设在1个MBS覆盖范围内有P个PBS,m个MUE,n个PUE,MUE的信干噪比(signal to interference plus noise ratio,SINR)如式(1)
(1)

(2)

根据香农定理,MUE速率为
Rm=BPRB·log2(1+SINRm)
(3)
同样的,PUE速率为
Rn=BPRB·log2(1+SINRn)
(4)
系统容量计算方法见式(5),其中BPRB表示单位PRB上的带宽,TP表示系统吞吐量
(5)
2 所提的能效优化算法
2.1 基站功率损耗模型
以宏基站和微微基站的功耗进行建模,基站的线性功耗模型采用文献[7]的功耗模型

(6)
式中:PTotal是整个基站功耗,NTRX是基站的发射天线数,P0是最小非零输出功率,Δ是与负载相关的功耗斜率,PT是基站发射功率,Pmax是基站最大发射功率,Psleep表示基站休眠时的功耗,本文不考虑基站睡眠情况。根据式(6)可得到MBS和PBS的功耗模型如下
PMacro=NTRX,M(P0,M+ΔMPT,M)0
(7)
式中:PMacro和PPico分别表示MBS和PBS的功耗,分别P0,M和P0,p表示MBS和PBS的最小非0输出功率NTRX,M和NTRX,P分别表示MBS和PBS的发射天线数,ΔM和Δp分别表示MBS和PBS与负载相关的功耗斜率,Pmax,M和Pmax,P分别表示MBS和PBS最大发射功率。Psys表示整个系统功耗。上述仿真参数模型见表1。
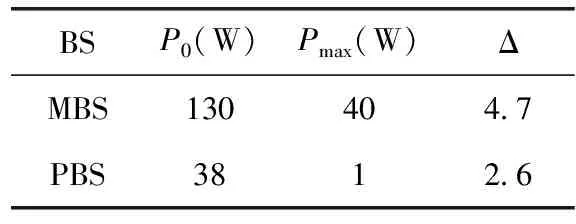
表1 功耗模型仿真参数
2.2 优化目标分析
将所有基站所获得的传输能力总和也就是系统吞吐量与基站功率消耗的比值EEsys作为衡量系统能量效率的标准[12],单位为bit/Joule,即消耗每焦耳能量时传输的比特数,由此得到式(8)
(8)
为了最大化系统能效,将上式能效表达式转化成式(9)进行求解
(9)
根据式(9)中的目标优化函数,为了在系统总功耗最小的情况下实现最大的系统容量[13],得到最优的系统能效,为此建立如式(10)所示的优化模型,其中,Pmax,P表示PBS基站所能承受的最大功率消耗
(10)
3 基于改进遗传算法的能效优化算法
遗传算法是指通过模拟达尔文自然进化选择的过程,对一个解集空间进行遗传操作并搜索,使群体经过优胜劣汰,最终在解集空间中找到最优解[14,15]。本文遗传算法应用于异构网络场景时,以系统能效为优化目标,PBS的发射功率作为遗传算法的初始解,改变进化过程中的交叉和变异概率使得解集趋向更优的方向进化,最终找到最优能效时的各PBS发射功率。
3.1 遗传算法的适应度函数
将式(9)中的能效目标优化函数EE(PT,1,PT,2,…,PT,P)作为遗传算法的适应度函数f(Ul),PBS的发射功率构成遗传算法中的初始解,即染色体的遗传编码,如式(11)所示,功率分配方案Ul的能效值由式(12)确定
(11)
(12)
其中,f(Ul)表示第l个功率分配方案对应的EE。Ul(l=1,2,…,L)代表第l个染色体的遗传表示,即第l个功率分配方案,每一个基因位XT,lp对应第l个功率分配方案下第p个PBS的发射功率Pp,L表示种群个数即功率分配方案个数。
3.2 改进遗传算法的种群初始化及选择复制
为了能够有效地得到最优解,加快算法的收敛性,对基本遗传算法初始化和选择过程进行改进。
若初始种群中每个功率分配方案对应的适应度函数最大值即最高能效值高于未使用遗传算法情况下的EEsys时,根据适应度值进行选择复制,否则重新生成初始种群。
为了得到较优的染色体个体,进行选择复制时,尽量使得更多表现优秀的个体作为父代参与交叉或变异。因此,将每个群体对应的适应度值从高到低进行排序,根据适应度值大小降序排列,种群数为L。将种群依次分为4等份,分别为UL1、UL2、UL3、UL4。去掉低适应度值部分UL4,将UL1复制两份,UL2、UL3各复制一份,原始种群变为UL1、UL2、UL3、UL1,既保证了保持种群数不变,又使更多较优个体参与交叉过程,如图2所示。

图2 选择复制原理
3.3 改进遗传算法的交叉与变异
传统的遗传算法中交叉概率和变异概率是固定的,个体参与交叉和变异的概率都是随机的,易导致最优解的丢失,算法过早收敛。根据个体适应度值的不同改变了个体的交叉和变异概率,避免的优秀个体的丢失,保证了算法的稳定性,使算法收敛于最优。为了减少算法复杂度,交叉选择二进制交叉中的单点交叉,变异选择二进制变异,对PBS的发射功率进行遗传操作的具体流程如图3所示。
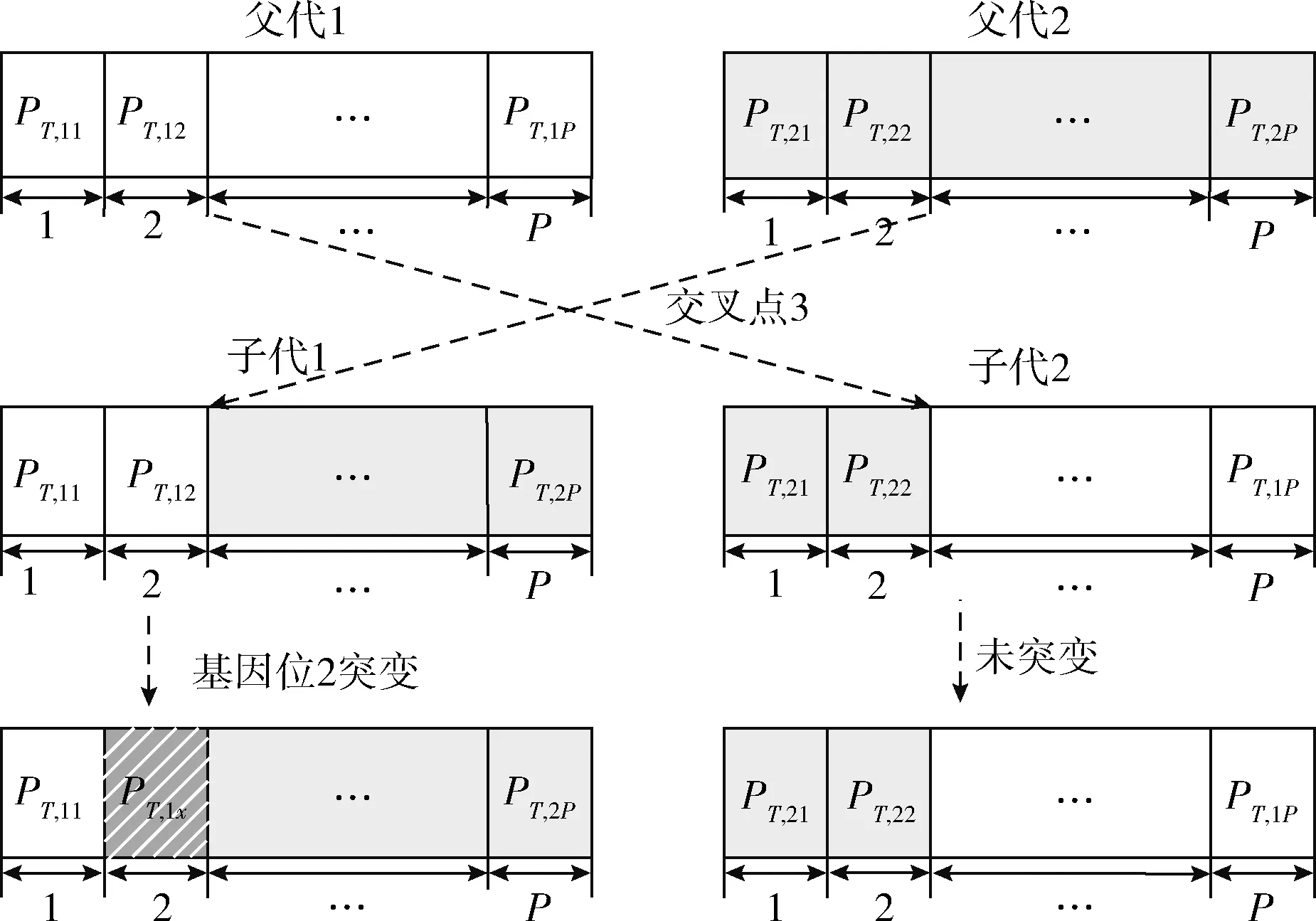
图3 遗传操作过程
图3中是两个父代染色体进行交叉变异产生新个体的过程,其中PT,lp(l=1,…,L,p=1,…,P)表示第l个功率分配方案中第p个PBS发射功率,PT,1x表示交叉后产生的子代1中基因位2突变重新生成的基因。
将上述改进遗传操作后的算法应用于异构网络,相应的能效优化步骤如下:
(1)计算异构网络下系统能效EEsys;
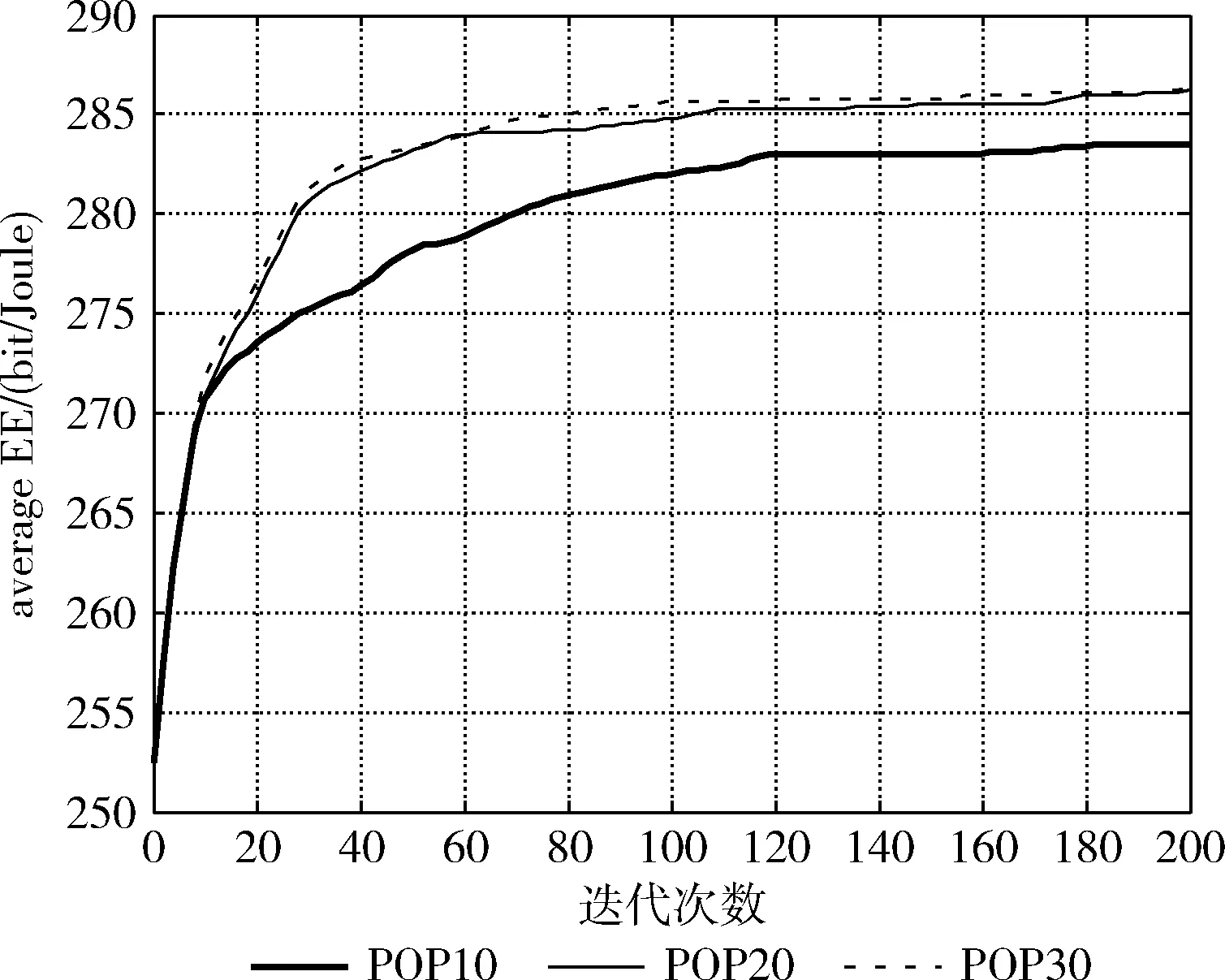
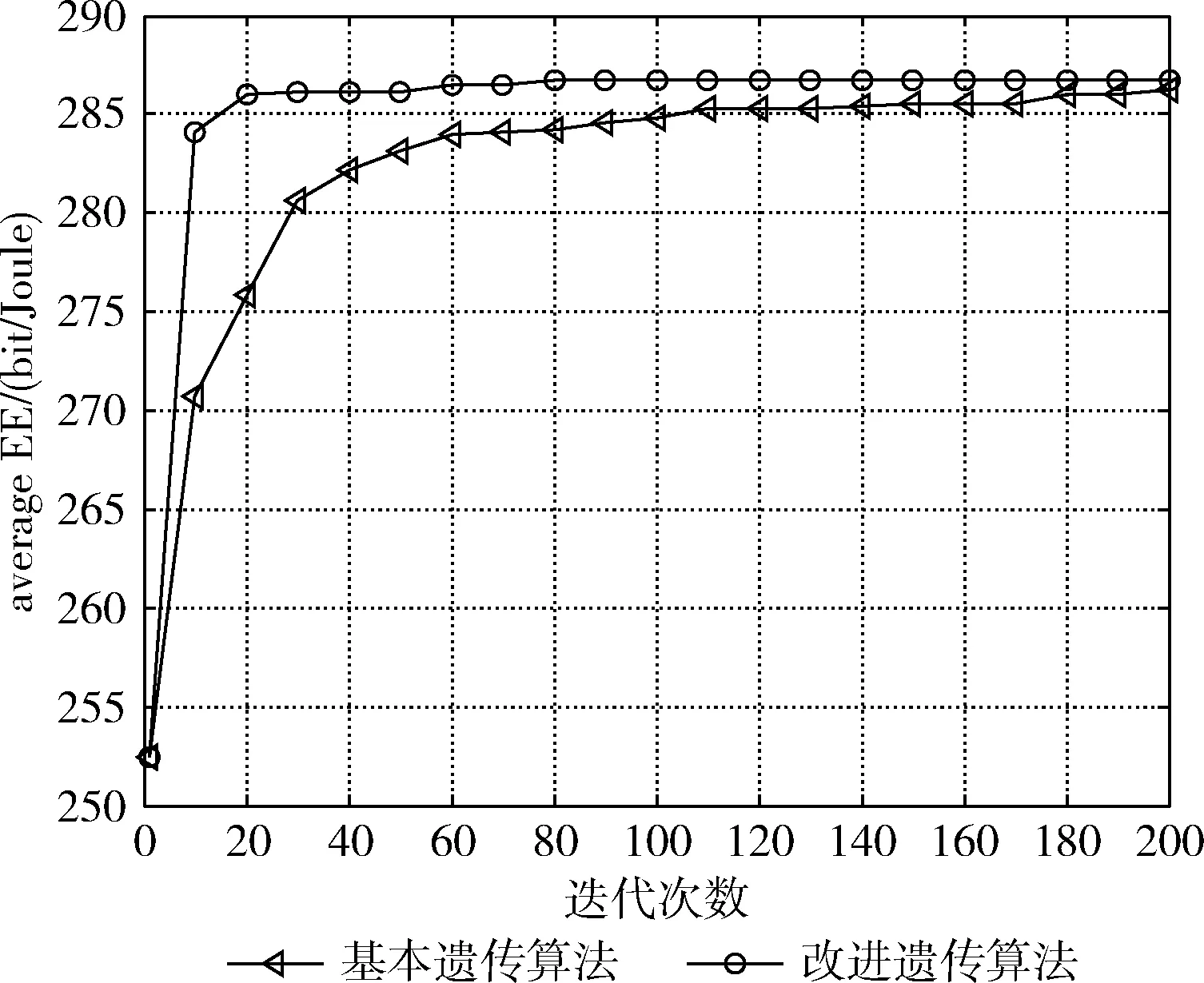
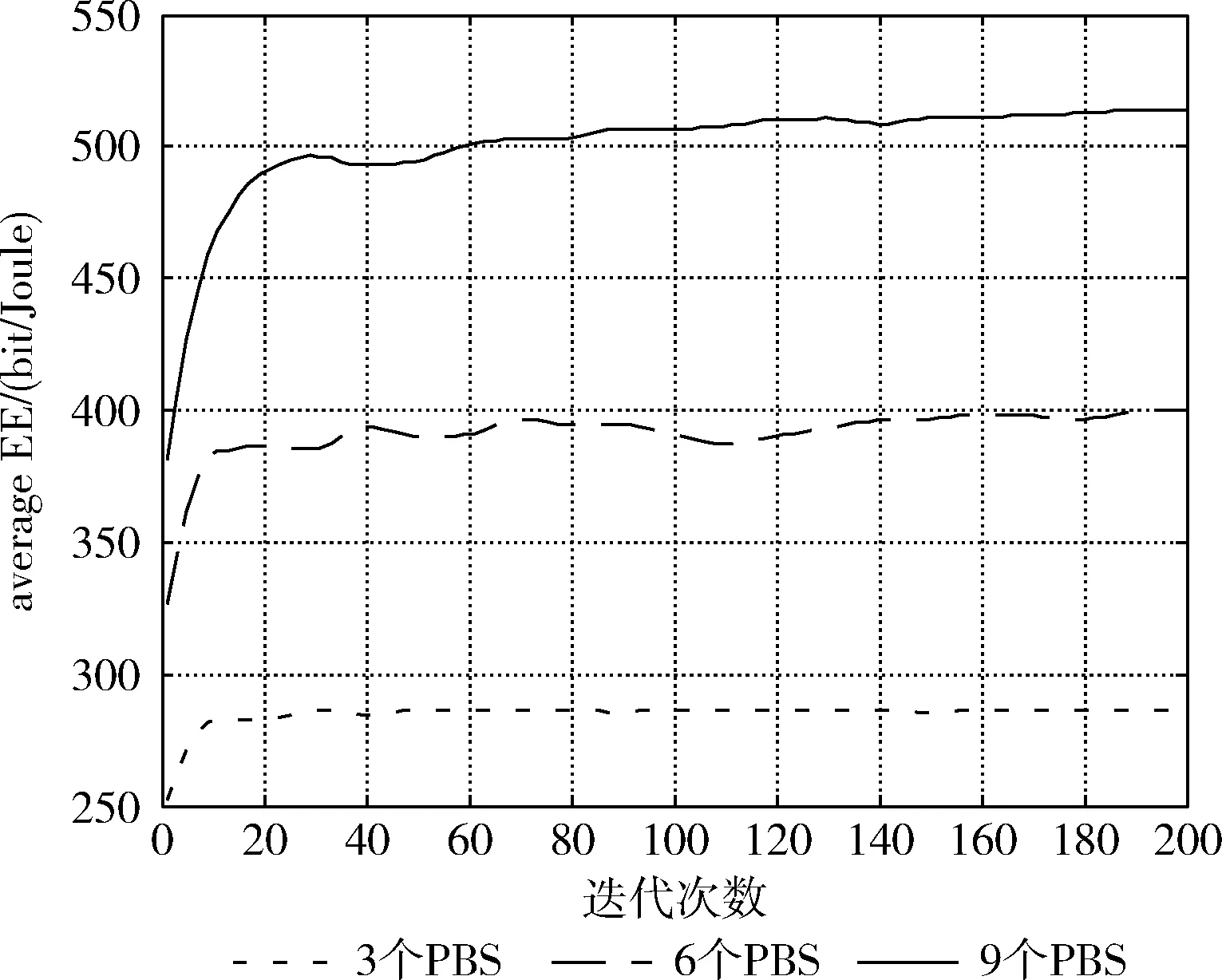
(2)在0≤PT,p (3)设置迭代次数θ,t=1(t≤θ); (4)ifEEsys>fmax,重复(2)、(3); else根据3.2节所提方法进行选择复制; (5)由3.3节知,iff(Ul)-EEsys>0,ifrand() end; end; (6)iff(Ul)-EEsys>0,不参与变异,保留遗传信息不变; end; (7)计算每次迭代的适应度均值作为此次迭代的系统能效值; (8)t=t+1,重复(2)-(7); (9)满足迭代次数θ,结束; 通过上述的遗传操作过程能够保留较优的一些个体参与杂交,防止较优的个体参与变异,避免较优解丢失的同时使得算法趋于更优解的方向进化,加快算法的收敛速度。 首先,根据基本遗传算法对系统能效进行优化,每次迭代中个体对应的适应度函数均值作为此次迭代的系统能效值,得出不同种群数目下的系统能效随着迭代次数的变化情况,如图4所示。仿真参数见表2。 图4 不同种群数下能效变化 表2 仿真参数设置 图4对比了种群数分别为10、20、30这3种情况下的能效变化情况,从图中可知,为了使得EE达到最优,当种群数较少时,需要较多的迭代次数才能找到最优解,收敛速度较慢。相应的,种群数较多时收敛速度较快,在较少的迭代次数前提下更容易找到较优的PBS功率分配方案。从图中得到种群数设为10时,EE在120次迭代时基本趋于稳定,种群数设为20与设为30时相比,能效变化不明显,在迭代次数将近100次时能效趋于稳定。种群数为10时,能效相对于初次迭代提升将近12%。同理,种群数为20和30时,能效提升将近14%。因此在后续仿真中考虑到算法的收敛性和复杂度,设置种群规模为20进行仿真。 根据改进的遗传算法对系统EE进行仿真,并与基本遗传算法情况下进行对比,如图5所示。通过调整PBS发射功率,减少了PBS对MUE的跨层干扰和对PUE的同层干扰,使得系统吞吐量得到提升,从而提高能效。但在PBS发射功率减少到一定程度时,PUE信干噪比降低,系统吞吐量不再提升,系统能效趋于稳定。图5中明显可以看出两种算法在迭代次数较少时收敛较快,随着迭代次数的增加,收敛速度逐渐下降,能效趋于平稳。基本遗传算法下能效在80次迭代时趋于平稳,而改进遗传算法基本在迭代数20时趋于平稳。两种算法在迭代数200时,能效达到最大值,而改进遗传算法基本在20次迭代时将近达到最大系统EE。因此,通过改进遗传操作,提高了算法的收敛速度,在较少迭代次数条件下得到较高的系统EE。 图5 遗传算法与改进遗传算法能效对比 图6对未使用遗传算法、基本遗传算法以及改进遗传算法情况下的用户信干噪比和用户吞吐量累积分布函数进行了对比。从右图中可以看出,应用遗传算法调整PBS发射功率,降低了其对宏用户的跨层干扰,以及PBS之间的同层干扰,用户信干噪比得到明显提升,而改进遗传算法与基本遗传算法区别不大。相应的,用户吞吐量累积分布如左图所示,总体来说,所提算法保证了用户的通信质量。 图6 用户信干噪比和吞吐量累积分布函数对比 图7通过改进遗传算法对不同微微基站数量下的能效变化进行了仿真。从图中我们可以看出3个微微基站时,EE基本在10次迭代趋于平稳,6个微微基站在20次迭代趋于平稳,9个微微基站在80次迭代趋于平稳。这是因为微微基站数目增多时,利用遗传算法进行功率分配变得更加复杂,增加了算法运行时间。3个PBS时,能效相对于初次迭代提升近14%,6个PBS时提升近22.4%,9个PBS时提升近31%。因此,随着PBS的增加,能效得到明显改善,验证了所提算法的有效性。 图7 不同微微基站数目与能效变化对比 在保证系统吞吐量最大,系统总功耗最小的前提下,将遗传算法应用于异构网络场景中,根据遗传算法调整PBS发射功率。以能效为优化目标,PBS发射功率作为遗传算法的初始解,提出一种基于功率控制的能效优化算法。首先,对不同种群数下的能效变化进行了仿真,仿真结果表明利用遗传算法进行功率控制能效得到一定提升。其次,改进遗传算法能够在较少的迭代次数条件下达到较优的系统能效,加快了算法的收敛速度,在一定程度上保证了用户服务质量。最后,改进遗传算法对不同PBS数目的能效变化进行了仿真,结果表明PBS数目增多时,能效得到明显提升。因此,通过改进遗传算法调整PBS发射功率,在提升系统能效的同时降低了系统功耗,验证了算法的有效性,实现了绿色节能的目的。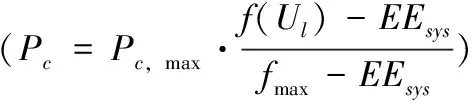

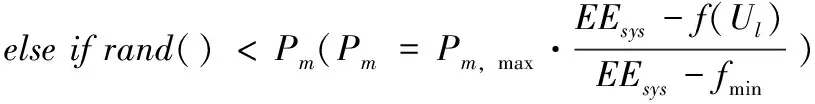
4 仿真结果与分析


5 结束语

