基于深度残差网络的图像隐写分析方法
高培贤,魏立线,刘 佳,刘明明
(武警工程大学 网络与信息安全武警部队重点实验室, 陕西 西安 710086)
0 引 言
传统的图像隐写分析方法是先提取特征,再利用分类器进行分类,例如富模型(RM)[1]+集成分类器(EC)[2]。随着深度学习在图像识别领域的优异表现,卷积神经网络(CNN)逐渐成为一种重要的图像隐写分析方法。Guangshuo Xu等构建了一个5层的CNN模型进行隐写分析,对S-UNIWARD算法的检测准确率达到了80.24%[3],但是CNN的缺点是随着深度的增加,网络模型会出现退化问题,模型识别准确率会很快达到饱和,然后迅速下降[4,5]。为了解决退化问题,何凯明等提出了深度残差网络(DRN),通过捷径连接改变网络结构,实现残差学习。何凯明等构建的152层DRN模型在ImageNet测试集中的识别误差为3.57%,在2015年的大规模视觉识别挑战赛中赢得了第一名[6]。
针对目前图像隐写分析效率较低的情况,本文提出了一个基于深度残差网络的神经网络模型(S-DRN)进行图像隐写分析。实验结果表明,相比Guanshuo Xu等的构建CNN模型,本文模型识别准确率提高了12.89%。
1 残差网络
1.1 退化问题
深度卷积神经网络的提出引发了图像分类方法的一系列突破[7-9],通过增加网络深度可以提取图像更加抽象的特征,从而提高模型识别准确率。随着网络深度的增加,梯度消失/爆炸问题会阻碍网络的收敛,批量规范化(BN)的提出使得深度网络利用随机梯度下降(SGD)得以收敛。但是,深度网络在训练过程中会出现退化问题,即随着网络层数的递增,网络识别性能会逐渐达到饱和后并迅速下降。退化问题并不是由于过拟合造成的[6],而是增加网络的深度会使得训练误差增加。退化问题表明了深度网络在训练过程中寻找最优权重参数存在很大的困难。
1.2 残差学习
在训练好的浅层网络基础上,通过增加网络层来拟合恒等映射,这种加深网络的方法使得训练误差不应高于其浅层网络模型,但退化问题表明利用非线性网络层去拟合恒等映射在求解上存在困难[6]。在CNN中,H(X)为若干堆叠的非线性网络层逐渐逼近的目标函数,其中X为网络的输入。与CNN不同的是,残差网络使用非线性网络层去拟合残差函数
F(X)=H(X)-X
(1)
这里假设输入与输出是相同维度。通过捷径连接,使得网络的输出为
H(X)=F(X)+X
(2)
虽然这两种方法都可以逐渐拟合出目标函数H(X),但是利用堆叠的非线性网络层学习残差值使其逼近于0值相对来说较为容易。因此,相比无参考函数的网络,残差网络使得网络进行参数最优化变得更加容易实现,且随着网络层数的增加可以获得更高的识别准确率。
如图1为1组残差学习模块。残差学习模块的输入为X,输出为
y=F(X,{Wi})+X
(3)
式中:Wi为权重矩阵,F(X,{Wi})为网络学习到的残差函数。当X与F(X,{Wi})维度不同时,通过在捷径连接上作线性投影Ws来实现输入输出之间的加法,即
y=F(X,{Wi})+WsX
(4)
为了简化符号,在输出公式中省略了偏差项。残差模块中必须至少含有两层卷积层,若只有一层卷积层,则残差模块为线性层,其输出为y=W1X+X,失去了残差学习的优势。

图1 残差学习模块
1.3 深度残差网络(DRN)
残差学习使得深度卷积神经网络的训练得以实现,随着网络层数的增加,模型的识别准确率也逐渐增加。在DRN的残差学习模块中,捷径连接特征图的大小和维度必须与残差特征图相同,否则不能实现捷径连接的输出与残差函数的加法。对于卷积操作带来的特征图大小变化,通过采用0元素填充使得特征图大小不变。当网络中的特征维度增加时,有两种方案实现维度相匹配。①对于维度增加带来的空缺元素补零。②通过线性投影来匹配维数,采用大小为1×1的卷积核来实现。整个网络仍然可以使用反向传播算法(BP)进行端到端的训练,不需修改求解方法,在很大程度上方便了网络的训练。
2 S-DRN模型
基于何凯明等的研究,本文提出了一个S-DRN模型进行图像隐写分析,如图2所示。在该模型中共有34层卷积层。这些卷积层可分为3类:高通滤波器层(HPF层),特征提取卷积层和残差学习卷积层,其中参与权重更新的是残差学习卷积层。
2.1 S-DRN网络层
在图像隐写分析领域,HPF层的是一种特殊的卷积层。其卷积核大小为5×5,通道数为1,权重为固定值F,且不随随机梯度下降(SGD)而更新。网络的输入经过HPF层预处理之后再进入特征提取卷积层。HPF层的使用可以加快网络的收敛速度
特征提取卷积层与CNN中的卷积层相同。该卷积层的卷积核与输入进行卷积操作,提取出输入的不同特征,第一层卷积层提取低级特征,更高层的卷积层提取更高级的特征[10]。当网络深度加深以及训练样本数量有限时,使用拟合好的卷积层可以避免过拟合以及缩短训练时间,该模型使用了拟合好的两层卷积层。
每个残差模块由两层残差学习卷积层组成,并通过捷径连接将残差函数与输入相加实现残差学习。当相邻残差模块之间维度相同时,捷径连接采用恒等映射。当相邻残差模块中卷积核个数增加时,在捷径连接中采用大小为1×1的卷积核来实现维度的增加。在残差模块中采用了大小为3×3的卷积核,共构建了16组残差学习模块。
在残差学习模块后采用了两层输出为1000维的全连接层和一层损失函数层,全连接层的神经元与上一层网络的神经元全连接,整合出卷积层中可以区分所属类别的局部特征。损失函数层采用的是Softmax损失函数,将输入分为两类。具体的分类问题需要考虑具体的损失函数。由于池化层对分类效果产生不好的影响,因此该模型没有使用池化层。

图2 S-DRN框架
2.2 模型分析
Guanshuo Xu等构建了一个5层CNN模型进行隐写分析,该模型由5组卷积模块组成,如图3所示,每组卷积模块由卷积层和池化层组成。前2组卷积模块采用TanH激活函数,后3组卷积模块采用ReLU激活函数。为了避免模型在训练过程中陷入局部最优化,在激活函数前都加入了批量正规化层(batch normalization layer,BN层)。输出层由一层全连接层和损失函数层组成。该模型在BOSSBass数据库上检测S-UNIWARD嵌入算法的准确率达到80.24%。
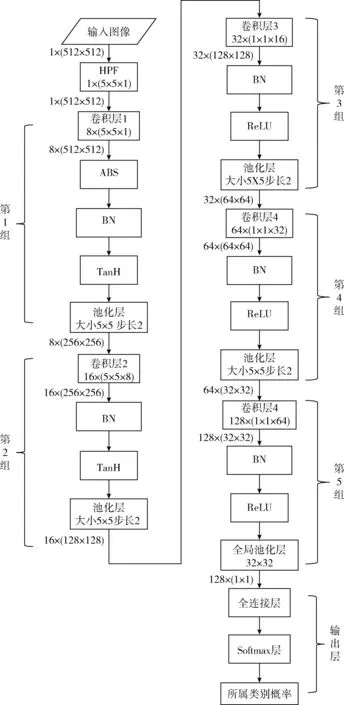
图3 Guanshuo Xu等构建的5层CNN模型
相比Guanshuo Xu等构建的CNN模型,S-DRN模型显著增加了网络的深度,并且利用残差学习解决了退化问题,有效提高了图像隐写分析效果;对于图像隐写分析来说,模型通过识别图像中嵌入的噪声进行分类,而池化层会弱化所嵌噪声,不利于最终的识别效果,因此S-DRN模型取消了池化层;由于残差网络的深度,在网络训练过程中会出现梯度消失/爆炸问题,导致模型不收敛或者收敛速度极慢。因此,每个模型都在卷积层之后增加了批量正规化层(BN层),以实现模型的收敛。BN层的使用还可以增加1%左右的识别准确率[11]。
2.3 网络对比
为了更好的评估深度残差网络,本文构建了3种网络进行对比实验。①浅层卷积神经网络:由两层卷积层组成,如图4(左)所示。②深度卷积神经网络:在浅层卷积神经网络的基础上,直接叠加32层卷积层,如图4(右)所示。③深度残差网络:在浅层卷积神经网络的基础上增加了16组残差学习模块,如图3所示。3种网络都使用相同的HPF层、全连接层、softmax层。
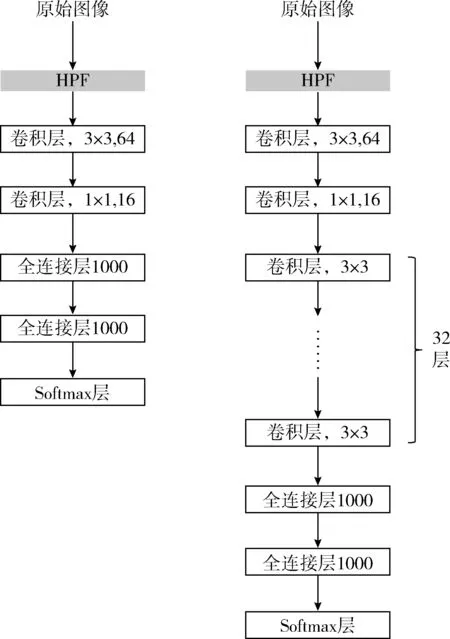
图4 浅层CNN(左)和深度CNN(右)
考虑到训练时间,将残差网络的中的残差模块改为如图5的瓶颈结构。3个网络层中卷积核大小分别为1×1、3×3和1×1。卷积核大小为1×1的卷积层是用来减少或恢复维度。通过这种结构改变使得卷积核大小为3×3的卷积层的输入和输出维度减小。这种结构的使用可以缩短训练时间,更加经济[6]。

图5 瓶颈结构
3 实 验
3.1 图像库及实验平台
本文使用的图像库是目前图像隐写分析最常用的BOSSbase图像库,由10 000张大小为512×512的pgm格式的灰度图像组成。为了增加训练样本的数量以及节约内存,实验中将图像裁剪为大小为128×128的图像,将16×104张图像作为载体图像,使用S-UNIWARD隐写算法对载体图像进行信息嵌入,嵌入后的图像作为隐写图像,嵌入率为0.4 bpp。将载体图像和隐写图像中的3/4作为训练集,其余的图像为测试集,训练集和测试集均为随机打乱的顺序并且不存在交集。残差网络同样使用BP算法进行端到端的训练,实验平台选择的是基于C++语言的深度学习仿真工具Caffe。
3.2 实验参数
与CNN相同,残差网络的训练使用随机梯度下降算法(SGD)进行优化。学习速率初始值为0.001,学习率变化策略为“inv”,避免了手动调整学习率参数,使学习率随着迭代次数的增加自动调整。由于GPU内存的限制,训练时最小批量大小为64,测试时最小批量大小为40。冲量参数(momentum)为0.9,权值衰减(weight_decay)为0.004。对模型迭代20 000次进行训练。为了更好地对比CNN和残差网络,在训练过程中网络都采用相同的参数。
3.3 实验结果
相比传统的图像隐写分析法,S-DRN模型较大的提高了图像隐写分析的检测准确率和检测效率;相比XU等[3]构建的5层CNN模型,S-DRN模型提取了更抽象的高级特征,并且解决了网络退化问题,提高了识别效果。实验结果见表1。

表1 各模型识别准确率
本文首先构建了两种CNN模型进行实验,这两种模型除卷积层不同外,其余各层以及参数均相同。实验结果表明,两层卷积层的CNN模型的识别效果优于一层卷积层的CNN模型,见表2。同时优于传统的隐写分析算法和XU等构建的5层CNN模型。

表2 浅层CNN模型识别准确率
在拟合好的两层CNN模型的基础上,对比了直接叠加的平凡网络和不同深度的残差网络。网络的深度直接影响识别效果,对于残差网络,网络越深,识别效果越好。但随着网络深度增加,网络参数急剧增多,需要更大的GPU内存以及更多的训练时间。因此,本文对比了3种不同深度的残差网络。结果如图6所示,残差网络的准确率明显高于浅层CNN和直接堆叠的平凡网络。
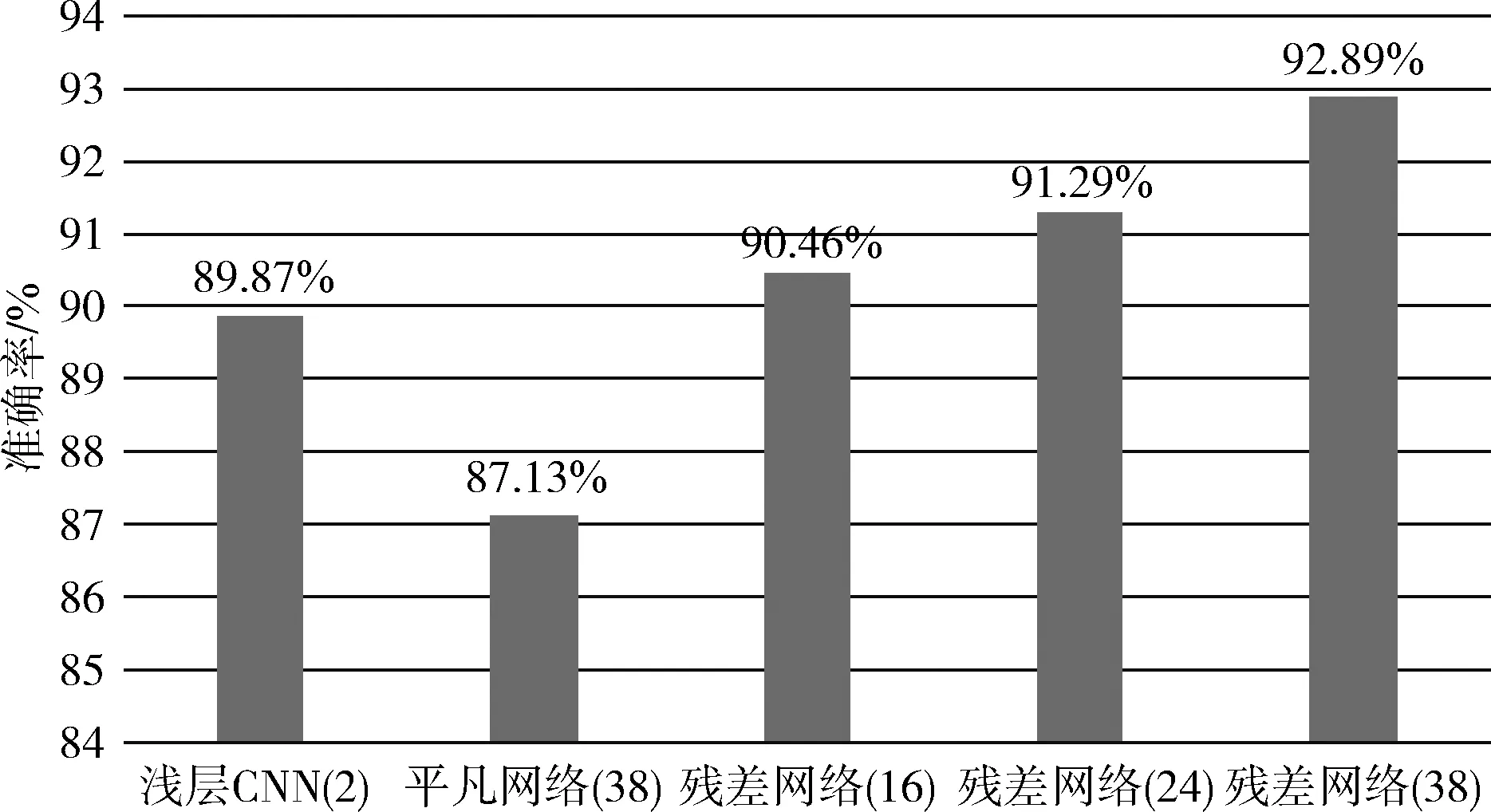
图6 3种类型的神经网络识别准确率
网络中池化层会弱化噪声,不利于最终的识别效果。因此,本文还对池化层对隐写分析检测效果的影响做了对比实验。实验结果见表3,池化层会降低模型隐写分析的准确率,因此在模型中取消了池化层。
对于图像隐写分析,HPF层极大地提高了模型的收敛速度,表4为S-DRN模型在迭代20 000次时有无使用HPF层的损失值和准确率对比结果,从表中可以看出,当训练20 000次时,无HPF层的模型损失值仍然没有收敛,分类结果接近于随机分类。
网络训练的损失值(loss)代表着网络的拟合程度,图7表明了平凡网络的拟合速度慢于残差网络,这也证明了神经网络随着深度的增加会出现退化问题,而残差网络可以有效解决退化问题。
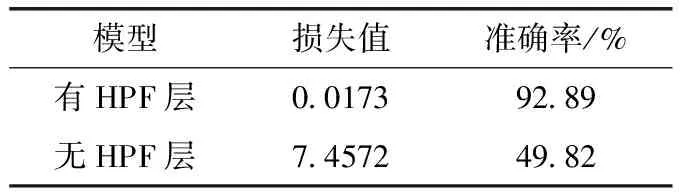
表4 有无HPF层的损失值和识别准确率

图7 平凡网络和S-DRN模型损失值(loss)
4 结束语
本文构建了一个深度残差网络模型进行图像隐写分析,增加了网络模型的深度,解决了退化问题,提高了识别准确率。实验结果表明,S-DRN在图像隐写分析邻域的表现优于浅层卷积神经网络和传统的图像隐写分析算法。但是,深度网络的训练相对于浅层网络比较耗时,下一步研究的方向是增强深度学习在隐写分析领域的准确性以及提高深度网络的训练效率。

