深度研读试题 启迪复习备考
安徽省临泉田家炳实验中学 (邮编:236400)
高考试题对复习备考有导向作用.因此,每年高考后,教师大都认真做高考试题,感受高考试题的变化.笔者认为仅限于此还不够,教师应深度研读高考试题,挖掘试题的来源,探寻试题的不同解法,并深度拓展试题,启迪高三复习备考.下面以2018年全国卷I文20(理19可看成它的变式)为例具体谈谈自己的看法,与大家交流.
1 试题呈现
设抛物线C:y2=2x,点A(2,0)、B(-2,0),过点A的直线l与C交于M、N两点.
(1)当l与x轴垂直时,求直线BM的方程;
(2)证明:∠ABM=∠ABN.
本题以抛物线为载体,以直线与抛物线的位置关系(相交)为依托,借助两角相等,综合考查直线、抛物线以及它们之间的关系等知识;在解决问题的过程中,进一步考查学生的逻辑推理与运算求解能力,从中渗透了直观想象、逻辑推理、数学运算等数学核心素养,综合性强,有一定难度.
2 试题来源
2.1 试题命制猜想
该试题改编自教材,过程如下:
(1)人教版数学选修2-1第73页第6题:“如图1,直线y=x-2与抛物线y2=2x相交于A、B两点,求证:OA⊥OB”;
(2)如图2,去掉线段OA、OB以及点F,然后取直线y=x-2与x轴交点M(2,0)及定点N(-2,0),连接NA、NB;
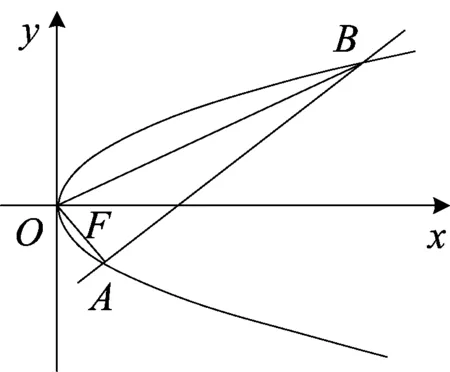
图1
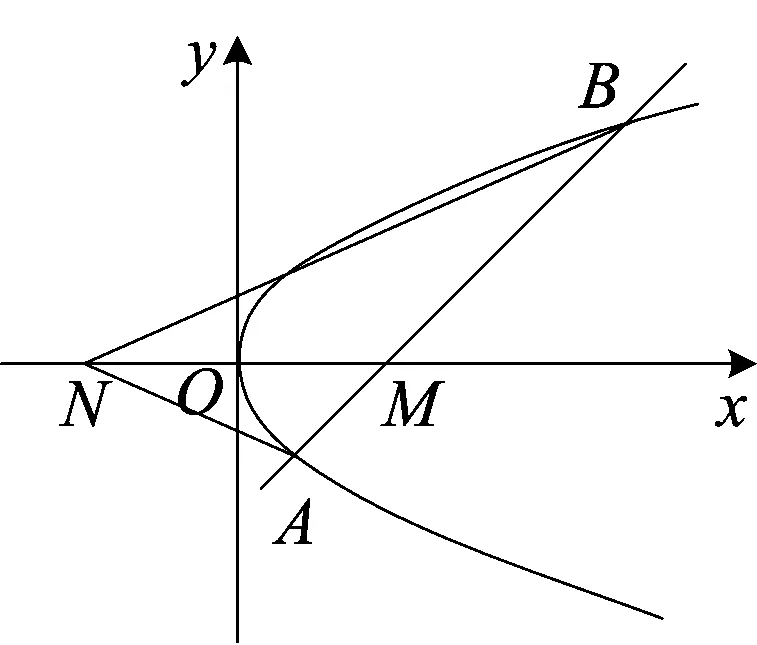
图2
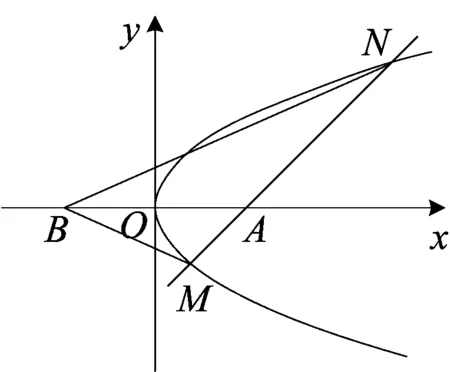
图3
(3)如图3,把直线y=x-2改为任意过M(2,0)的直线l,并把相应的字母交换,就得到试题.
2.2 改编前后对比
试题保持了教材中抛物线和点(2,0)不变,把直线y=x-2一般化,并添加了与点(2,0)关于原点对称的点(-2,0),而结论也由线垂直改为角相等.通过这样的改编,使得试题的深度和灵活性都得到大幅度地提高,符合高考命题(源于教材,又高于教材)的要求.
3 试题解法
3.1 解法
(1)是求特殊位置(直线l与x轴垂直)下的直线方程,易得直线BM的方程为x-2y+2=0或x+2y+2=0(过程略).对于(2),由于∠ABM与∠ABN的公共边在x轴上,另外两边分居x轴的两侧,故证∠ABM=∠ABN主要有四条思路:利用角平分线定理的逆定理,直线BM、BN的斜率之和为零以及三角形相似.由于当直线l垂直x轴时,易证∠ABM=∠ABN,只考虑直线l不垂直x轴的情况.
解法1利用角平分线定理1的逆定理
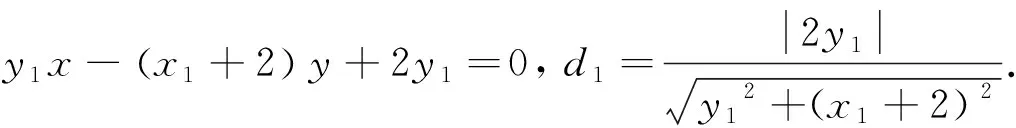
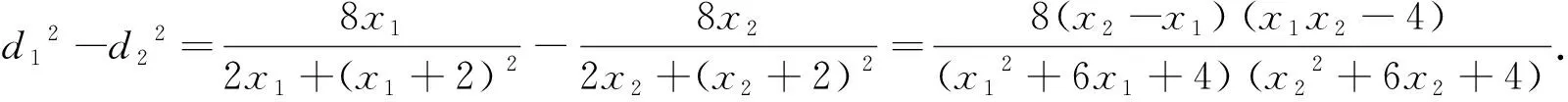
解法2利用角平分线定理的逆定理
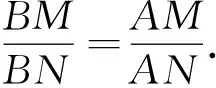
设直线l的方程为y=k(x-2),M(x1,y1),N(x2,y2),

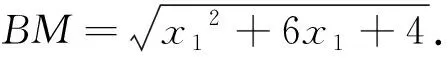
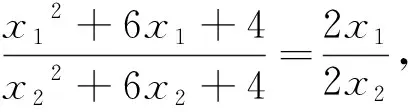

解法3利用两直线的斜率之和为零
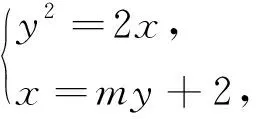
因为M(x1,y1),N(x2,y2)都在直线l:x=my+2上,所以x1=my1+2,x2=my2+2.
因此kBM+kBN=

=∠ABN.
解法4利用三角形相似
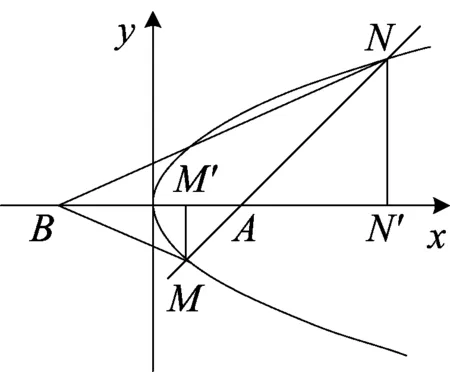
图4
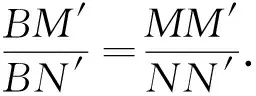
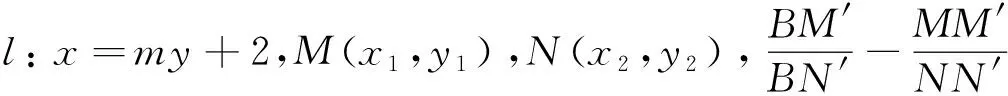
故∠ABM=∠ABN.
当然也可以借助BM上关于x轴对称的点在BN上,或者向量法证明.
3.2 解法对比
四种解法都是以直线与抛物线相交为基础,在设而不求思想的指导下,通过消元建立关于x或y的一元二次方程,利用韦达定理得到等式,为证明命题做准备.其中方法1与方法2直接利用角平分线定理的逆定理,具有初中知识背景,容易想到,但是对运算能力要求较高,对一般的学生是一种挑战,一般不提倡用它.方法3是把角相等转化为斜率之和为零,相对于前两种方法,运算量减少,但思维量增大,这是师生一般采用的方法.方法4侧重于几何法,构造三角形相似,简化了运算量,但学生不易想到.四种方法各有千秋,只有让学生亲身感受解题的过程,才能深刻领会各种方法的优缺点.
4 试题拓展
4.1 拓展
拓展1设抛物线C:y2=2px(p>0),点A(a,0),B(-a,0)(a>0),过点A的直线l与C交于M、N两点,那么∠ABM与∠ABN是否相等?
拓展2已知A、B、C、D是抛物线E:y2=2px(p>0)上的四点,A、C关于抛物线的对称轴对称且在直线BD的异侧,直线l:x-y+1=0是抛物线在C点处的切线,BD∥l,那么AC平分∠BAD吗?
拓展3设圆C:x2+y2=r2(r>0),点A(a,0),B(-a,0)(0 (1)当l与x轴垂直时,求直线AM的方程; (2)设O为坐标原点,证明:∠OMA=∠OMB. 4.2 拓展分析 在试题的基础上,通过变换载体(从抛物线到圆、椭圆再到双曲线)实现横向拓展,在同一载体(抛物线、椭圆)下变换条件进行纵向拓展,力求举一反三,打通知识间的纵横联系,开拓视野,发展学生的思维能力. 5.1 复习备考,注重教材的深度挖掘 复习备考的主要目的是解高考题.关于如何解高考题,罗增儒教授曾指出:“教材是高考命题的基本依据.有的试题直接取自教材,或为原题、或为类题;有的试题是教材概念、定理、例题、习题的改编;有的试题是教材中的几道题目、几种方法的串联、并联、综合与开拓;少量难题也是按照教材内容设计的,在综合性、灵活性上提出较高要求.”[1]在谈到复习备考时,章建跃博士曾强调:“高考复习教学,基本而重要的是使学生系统掌握课本知识,形成良好的数学认知结构.这是教师应作、能做且必须做好的工作.不能抛开课本搞复习!”[2]由此可见,教材在复习备考中的重要性.在复习备考中,教师要依托教材,对教材深度挖掘,不仅要串联起相关的数学知识,还要对一些例题、习题加工整合,必要的话可适度拓展.对于“复习就是讲题”,“复习无需教材”等片面的备考观要引起重视,实践证明,任何脱离教材的备考都是不靠谱的. 5.2 复习备考,注重习题的深度解析 众所周知,高考数学科的考试时间有限且极其珍贵,如何节约时间将是影响高考成绩的重要因素.而高考试题的设置往往入口宽,解法多样,这就要求学生在短暂的时间内选择最优的解法(如文20的思路3与思路4).这种最优法选择的培育源于平时教学,源于复习备考.而复习备考主要是让学生学会解题.解题就是寻找题目的条件与结论之间的通达路径,路径不同,解法亦不同. 有的路径曲曲折折,但沿途风景优美;有的路径平坦通达,但略显乏味.只有让学生亲身体验,才能品味到个中的滋味,才能在解题中灵活应用.因此,在复习备考的途中,对于解法多样的习题,教师要有足够的耐心,深度解析各种方法,让学生在比较中开拓思路;教师不能以赶进度为借口,选择一种自认为合适的解法,草率的结束了事,这样不利于学生思维的发展和解题能力的提升. 5.3 复习备考,注重习题的深度拓展 复习备考,时间紧、任务重,教师往往为了赶时间、赶进度,把有“内涵”的试题轻易地放过了.表面上题没少讲,但实际上效果并不佳,再遇到类似的题目学生仍不会做,或看起来会做就是做不对,复习的效果可想而知.教师应抓住有“内涵”的试题不放手,不仅深度解析试题,还要在此基础上加以拓展,让学生通过一道题看透一类题,“拔出萝卜带出泥”.这样可以避免“刷题”带给学生的体力劳动,保证做适量的题达到有效复习备考的目的. 总之,在高考试题面前,教师要做一个“有心”人,既认真做高考题,又要抱着一种欣赏的态度,从不同方面、不同角度深度研读它.唯有这样,才能取得收获,获得启迪,进而提升复习备考的效果.
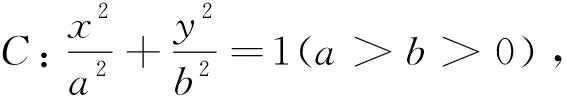
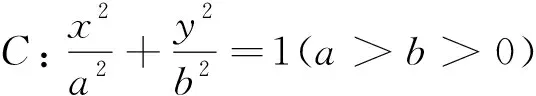
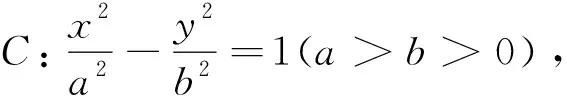
5 复习备考启示

