2018年高考全国I卷理科数学第18题解法探究

湖南师范大学数学与统计学院 (邮编：410081)

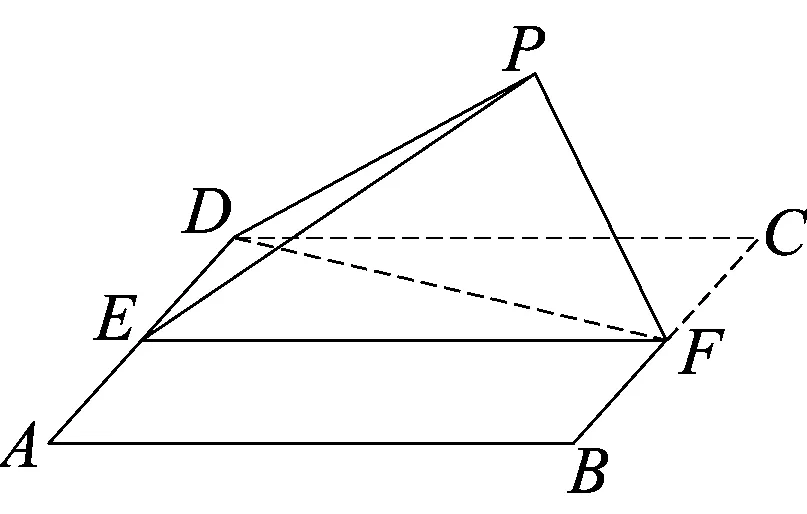
图1

题目如图1，四边形ABCD为正方形，E、F分别为AD、BC的中点，以DF为折痕把△DFC折起，使点C到达点P的位置，且PF⊥BF.

(1)证明：平面PEF⊥平面ABFD；

(2)求DP与平面ABFD所成角的正弦值.

本题主要考査直线与平面垂直、平面与平面垂直的概念、性质及判定方法，以及直线与平面所成角的有关知识，考查空间想象能力、推理论证能力，考査化归与转化思想，难度适中.对于这道题第(1)问，考査面面垂直的判定，比较简单，属于送分题.本文主要研究第(2)问，从不同知识的联系出发，给出多种解法.

解析(1)要证明面面垂直，首先想到面面垂直的判定定理，由线线垂直→线面垂直→面面垂直.题目中出现中点，目的就是要利用中位线的性质，据此思路，可得下列解法：

由E、F分别为AD、BC的中点，可得EF∥AB，故BF⊥EF,同时已知BF⊥PF,所以BF⊥平面PEF.又BF⊂平面ABFD，所以平面PEF⊥平面ABFD.

(2)本小问的解法多，思路宽，下文中将给出一些有代表性的解题思路.传统的解法有: 定义法和坐标法，首先介绍定义法．

为了解题的方便，先设正方形ABCD的边长为2.

I定义法

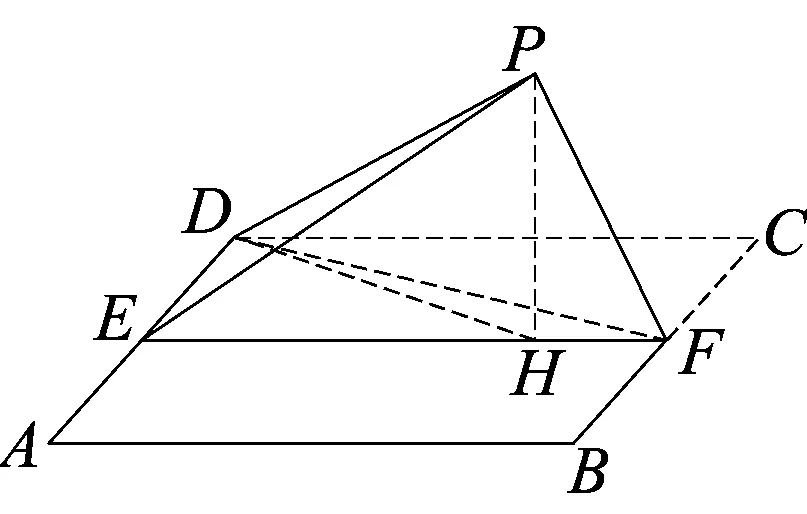
图2

如图2所示，过P作PH⊥EF,垂足为H.由(1)得PH⊥平面ABFD，故∠PDH即为直线DP与平面ABFD所成的角.

解法1(勾股定理)由(1)知，DE⊥平面PEF,因此DE⊥PE.设PH=x,则

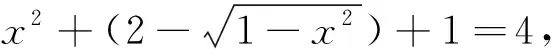
定义法，也称几何法，解题过程中经常要引入辅助线和回忆大量的几何定理公理，对学生的空间想象能力和逻辑推理能力要求较高.对于本题，运用定义法的关键在于找出直线DP与平面ABFD所成的角，并构造三角形.其中，求出点P到平面ABFD的距离是至关重要的得分点，如前所述，对于PH的求法是多种多样的.在教学过程中，我们应引导学生优先考虑用几何法解题，会动手操作、尝试着去处理图形，即对图形进行分割、补全、折叠、展开、添加辅助线等，借此不断提髙学生的空间想象能力，另一方面，让学生熟练掌握初中、高中几何定理公理的运用.

有些题目无论是找角(线面夹角、二面角的平面角)，还是求线段的长度都有一定的难度，而坐标法是一种万能的方法.下面我们就利用向量坐标的运算来求解本题．

II 坐标法

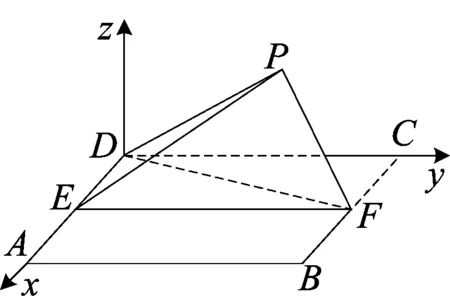
图3

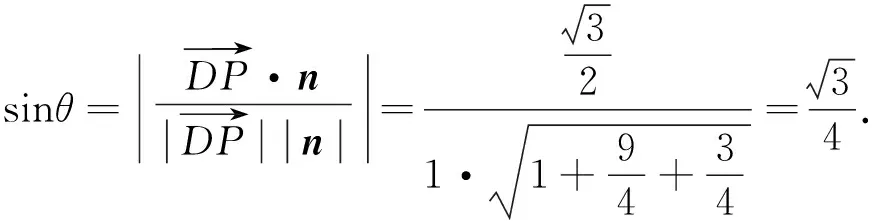
上述解法仅用到了本题的已知条件——PF⊥BF，PF⊥DP，极大降低了立体几何的思维难度，可有效降低减轻学生的心理障碍.对于坐标系的建立，以及根据题目中的条件列方程求解也有若干种不同的方式，在此就不再赘述.以上都是利用初等数学的思想解题，有些层次高的学生甚至提出了更高的观点，可以用空间解析几何的知识作答，下面将此想法进行完善：

解法5设DP与x轴、y轴、z轴的夹角分别为α、β、γ,则sinθ=cosγ,此题转化为求解cosγ.由三角恒等式：cos2α+cos2β+cos2γ=1,可以先求解cosα、cosβ,进而得到cosγ.

图4

坐标方法主要是利用向量的相关知识及其运算来解决问题，即用代数的方法解决几何问题，将数与形完美地结合起来，降低了立体几何的思维难度，解题有一定的规律性，便于学生掌握.

在教学中，可以鼓励学生从不同的角度解决立体几何问题，哪怕受教学时间的限制，在课堂上尽可“择其善者而从之”，但对另外的方法应稍作提示引导，让学生在课下尝试、讨论，并对不同的方法进行比较，以此来提高学生的能力.