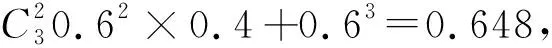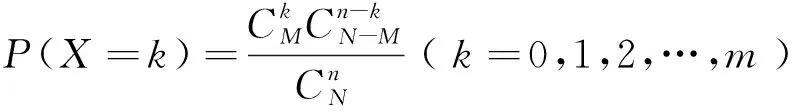一道2018年全国卷高考试题的商榷
——兼谈二项分布和超几何分布
山东省济南市教育教学研究院 (邮编:250001)
概率是新课改以后中学数学新增的教学内容,它与现实生活紧密联系,有很强的实用性.二项分布和超几何分布是两个应用广泛的重要概率模型,生活中的许多问题都可以利用这两个概率模型来解决,在近年的高考试题中经常出现,二者既有联系又有区别,因此正确区分并理解这两个概率模型至关重要.
1 高考真题与参考答案
2018年新课标I卷20题:
某工厂的某种产品成箱包装,每箱200件,每一箱产品在交付用户之前要对产品作检验,如检验出不合格品,则更换为合格品.检验时,先从这箱产品中任取20件作检验,再根据检验结果决定是否对余下的所有产品作检验,设每件产品为不合格品的概率都为p(0 (1)记20件产品中恰有2件不合格品的概率为f(p),求f(p)的最大值点p0. (2)现对一箱产品检验了20件,结果恰有2件不合格品,以(1)中确定的p0.作为p的值.已知每件产品的检验费用为2元,若有不合格品进入用户手中,则工厂要对每件不合格品支付25元的赔偿费用. (i)若不对该箱余下的产品作检验,这一箱产品的检验费用与赔偿费用的和记为X,求EX; (ii)以检验费用与赔偿费用和的期望值为决策依据,是否该对这箱余下的所有产品作检验? 参考答案 令f′(p)=0,得p=0.1.当p∈(0,0.1)时,f′(p)>0;当p∈(0.1,1)时,f′(p)<0. 所以f(p)的最大值点为p0=0.1. (2)由(1)知,p=0.1, (i)令Y表示余下的180件产品中的不合格品件数,依题意知Y~B(180,0.1),X=20×2+25Y,即X=40+25Y, 所以EX=E(40+25Y)=40+25EY=490. (ii)如果对余下的产品作检验,则这一箱产品所需要的检验费为400元, 由于EX>400,故应该对余下的产品作检验. 商榷1原题目中“先从这箱产品中任取20件产品作检验”,任取20件产品是有放回还是无放回,这涉及适用的概率模型是二项分布还是超几何分布?题目中没有明确说明20件产品的抽样过程,按照题目的表述,20件产品的抽样过程应该理解是不放回的抽样,因此,该题目中第一问的“20件产品中恰有2件不合格品的概率”应该按照超几何分布概型来计算.参考答案按照二项分布来计算,默认是有放回的抽样. 商榷2原题目中“设每件产品为不合格品的概率都为p”.每件产品是否为不合格产品是该产品的内在禀赋,它不存在不确定性.不确定性来自对总体的随机抽样而产生,因此,正确的表述应当是“每次抽样时,抽样的产品为不合格品的概率为p”. 商榷3原题目中“且各件产品是否为不合格品相互独立”.各件产品是否为不合格品不存在不确定性,不确定性来自抽样过程中,各件产品抽中为不合格产品是相互独立的. 商榷4原题目中“(ii)是否该对这箱余下的所有产品作检验?”根据待命题的否定,怎样叫不检验,是全不检验吗?还是不全检验?是否的真正含义是什么? 商榷5原题目中“(ii)是否该对这箱余下的所有产品作检验?”余下指的是这一箱余下的还是全部产品余下的,题目没有界定清楚. 表1 表2 超几何分布与二项分布都是取非负整数值的离散分布,表面上看,两种分布的概率求取有截然不同的表达式,但看它们的概率分布列,会发现构造上的相似点,如:随机变量X的取值都从0连续变化到l(l=min(n,M)),对应概率和N,n,l三个值密切相关,可见两种分布之间又有着密切的联系. 一般来讲,超几何分布和二项分布最明显的区别在超几何分布是“无放回”抽样,二项分布是“有放回”抽样 例1(2018年天津卷16)已知某单位甲、乙、丙三个部门的员工人数分别为24、16、16. 现采用分层抽样的方法从中抽取7人,进行睡眠时间的调查. (I)应从甲、乙、丙三个部门的员工中分别抽取多少人? (II)若抽出的7人中有4人睡眠不足,3人睡眠充足,现从这7人中随机抽取3人做进一步的身体检查. (i)用X表示抽取的3人中睡眠不足的员工人数,求随机变量X的分布列与数学期望; (ii)设A为事件“抽取的3人中,既有睡眠充足的员工,也有睡眠不足的员工”,求事件A发生的概率. 分析本小题主要考查随机抽样、离散型随机变量的分布列与数学期望、互斥事件的概率加法公式等基础知识.考查运用概率知识解决简单实际问题的能力.在第二问中,本题是典型的超几何分布,不放回,“睡眠充足”与“睡眠不足”两类,所以随机变量X~H(3,4,7) 例2(2015全国卷4)投篮测试中,每人投3次,至少投中2次才能通过测试.已知某同学每次投篮投中的概率为0.6,且各次投篮是否投中相互独立,则该同学通过测试的概率为( ) (A)0.648 (B)0.432 (C)0.36 (D)0.312 从极限的角度来分析,随着样本个数的增加,样本个数越大超几何分布和二项分布的对应概率相差就越小,当样本个数为无穷大时,超几何分布和二项分布的对应概率就相等,换言之,超几何分布的极限就是二项分布.但对于高中生的概率学习来讲,还是以各自分布的特征为区别,正确选择公式.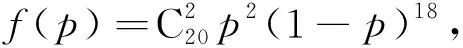
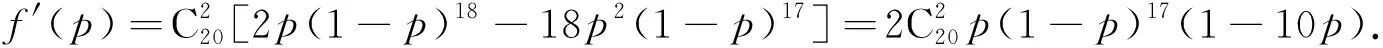
2 高考题的几点商榷
3 二项分布与超几何分布的概念回顾

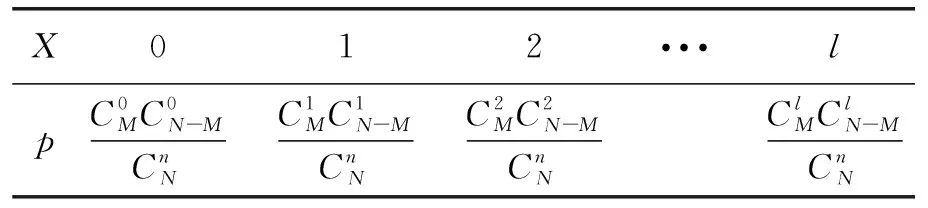
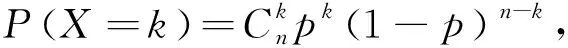
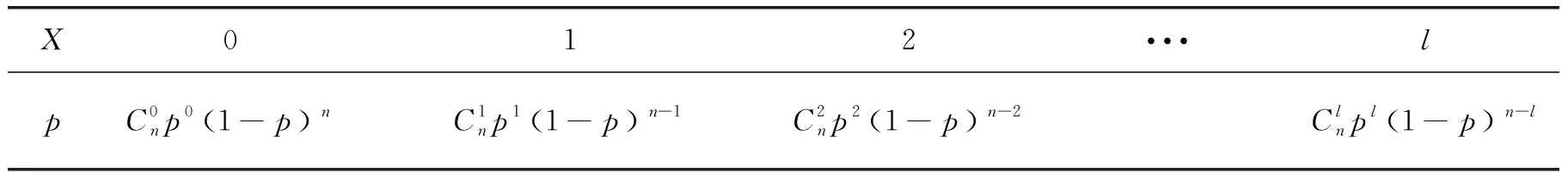
4 二项分布与超几何分布的区别与联系
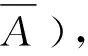
5 二项分布与超几何分布的应用举例