巧分类 细解题

章 丽

等腰三角形是特殊而又十分重要的三角形，一直受到各地中考命题者的青睐.同学们往往会因为考虑不全面而出现解答不完整的情况.在解决这类问题时，常常少不了关于角（顶角或底角）、关于边（腰或底边）的分类讨论.本文就从“角”的角度入手关注几例：

【例1】（2017·浙江丽水）等腰三角形的一个内角为100°，则顶角的度数是________.

【解析】等腰三角形的一个内角为100°，100°角是钝角，因此只能是顶角，不能为底角.故例1答案为100°.

【例2】（2018·浙江义乌改编）等腰△ABC中，∠A=80°，求∠B的度数.

【解析】等腰△ABC中一个内角∠A为80°，所以当∠A为顶角时，则底角∠B=50°；当∠A为底角时，∠B可能是顶角，也可能是底角，则∠B=20°或 80°.故答案为 50°或 20°或80°.注意本题有两个层次的分类讨论.

【归纳】对于一个等腰三角形，若条件中并没有明确顶角或底角时，应注意分类讨论，先确定这个已知角是顶角还是底角，再运用三角形内角和定理求解.

【例3】（2018·黑龙江哈尔滨）在△ABC中，AB=AC，∠BAC=100°，点D在BC边上，连接AD.若△ABD为直角三角形，则∠ADC的度数为________.

【解析】根据等腰三角形的性质可以求得∠B=∠C=40°，类比等腰三角形确定顶角“身份”，则直角三角形要确定直角“身份”，如果无法确定，则需分类讨论.所以已知△ABD为直角三角形，则直角可能是∠ADB 或∠BAD.如图 1，当∠ADB=90°时，则∠ADC=90°；如图 2，当∠BAD=90°时，则∠ADB=50°，∠ADC=130°.故答案为90°或130°.

图1

图2

【例4】（2018·湖北武汉）以正方形ABCD的边AD作等边△ADE，则∠BEC的度数是________.

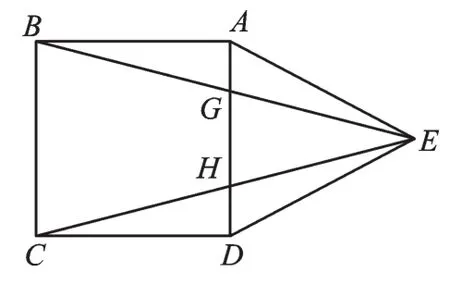
图3

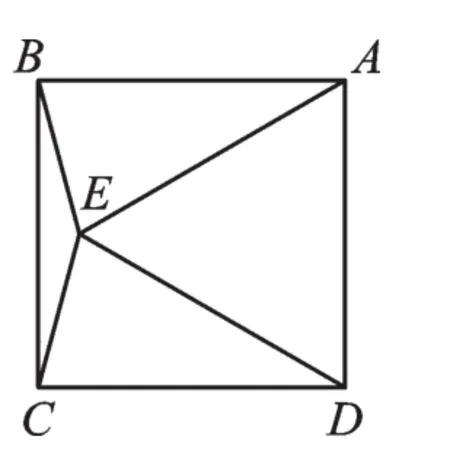
图4

【解 析】∠BAD=∠ABC=∠BCD=∠ADC=90°，∠AED=∠ADE=∠DAE=60°，AB=AD=CD=DE=AE，但不确定等边△ADE在正方形的内部还是外部，故需分成两种情况分别求解.如图3，∠BAE=∠CDE=150°，得∠AEB=∠CED=15°，则∠BEC=30°.如图4，∠BAE=∠CDE=30°，得∠CED=∠ECD=75°，∠ABE=∠AEB=75°，则∠BEC=150°.故答案为30°或150°.

解决与图形相关的问题时，常会出现图形中相关元素的“身份”不确定，或图形位置的不确定等情况.我们首先需要认真审题，逃出“陷阱”，然后锁定合理的分类标准，对各种情况逐一进行讨论求解，做到不重不漏.

（作者单位：江苏省无锡市水秀中学）