没有定“型” 分“类”讨论
顾云霞
同学们在学习“轴对称图形”这章时,常遇到计算线段长的问题.但因题目中的相关量没有定“型”,我们常常会由于考虑不全面而漏解或错解.下面从三种典型错误出发,通过错因剖析和正确解答,希望对同学们有所启示.
一、没有定“角色”——讨论边长“角色”
【例1】等腰三角形的两边长分别为5、8,则它的周长为( ).
A.13 B.18
C.21 D.18或21
【错解】选B;或选C.
【错因剖析】此题因没有对5、8两边长在等腰三角形中的“角色”进行讨论,而出现漏解;但有些问题若只考虑边的“角色”,遗忘了用三角形的三边关系来判断能否围成三角形,又会出现多解,导致出错.故涉及等腰三角形的边长问题,既要考虑到边长“角色”,还要顾及三边关系,考虑问题要周到全面.
【正解】选D.若5为腰长,且三条长为5、5、8的线段能构成三角形,所以周长为5+5+8=18;同理,若8为腰长,也能构成三角形,则周长为5+8+8=21.
【变式】一个等腰三角形的两边长分别为4、8,则它的周长为( ).
A.12 B.16 C.20 D.16或20
(正确答案:C)
二、没有定位置——讨论交点位置
【例2】在△ABC中,BC=10,AB的垂直平分线与AC的垂直平分线分别交BC于点D、E,且DE=4,则AD+AE的长度为_____________.
【错解】根据题意画草图,如图1所示,AD+AE=BD+CE=BC-DE=10-4=6.

图1
【错因剖析】由于没图,不少同学常画如图1所示的图形,故漏解.因为两条垂直平分线与BC交点D、E的相对位置没有确定,故要讨论交点D、E的位置,分两种情况作答.
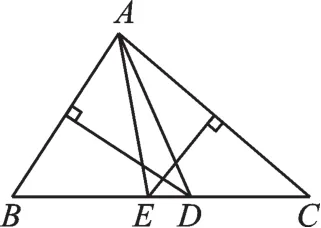
图2
【正解】根据题意,除了图1情形,还存在如图2所示的情况,此时AD+AE=BD+CE=BC+DE=10+4=14.故此题答案为6或14.
三、没有定图形——讨论图形形状
【例3】(2016·内蒙古通辽)等腰三角形一腰上的高与另一腰的夹角为48°,则该等腰三角形的底角的度数为__________.
【错解】如图3,由题意可知,∠ABD=48°,∠ADB=90°,所以∠A=42°,所以底角∠C=(180°-42°)÷2=69°.

图3
【错因剖析】此题同样需要画图分析、很多同学习惯了画顶角是锐角的等腰三角形,腰上的高自然在形内,却忽略了顶角是钝角的等腰三角形腰上的高线在形外的情况,故此题要分顶角是锐角的等腰三角形与顶角是钝角的等腰三角形两种形状讨论.
【正解】除了图3以外,还有图4,∵∠ABD=48°,∠ADB=90°,∴∠DAB=42°,∴21°.故此题答案为69°或21°.
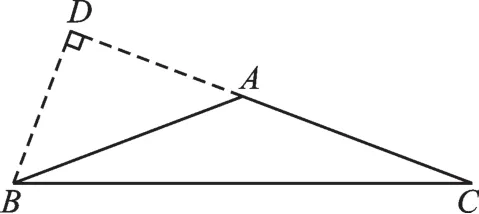
图4
【变式】等腰三角形一边上的高与一腰的夹角为48°,则该等腰三角形底角的度数为__________.(正确答案:42°;69°或21°)
总之,我们需要仔细审题.如果由已知条件无法确定相关元素的“角色”、图形位置、形状等,那么同学们就要小心谨慎,结合基本概念、基本图形,找准不确定元素的类别,分情况讨论,从而逐步培养自己缜密细致的思维习惯.


