一种大推力凸极永磁直线同步电机特性分析*

汪旭东，翟中飞，许孝卓，孙伟翔，师宇飞

(河南理工大学 电气学院，河南 焦作 454000)

0 引 言

近年来，随着矿山开采深度的不断延伸，高层建筑不断向空中延伸，传统曳引提升系统的局限性愈发凸显：

(1)一次性提升高度受到钢丝绳单位长度绳重、钢丝绳强度、根数及安全系数的影响，大部分情况下需要多级提升[1]。且钢丝绳过长易变形，引起轿厢震动严重从而造成提升系统控制困难；

(2)提升速度受钢丝绳缠绕速度所限，无法满足人们对于提升机高度运行的需求[2]；

(3)占用大量建筑空间，导致成本巨大[3]。

为解决上述问题，亟待提出一种新的提升模式。由于永磁直线同步电机(PMLSM)具有结构简单、力能指标高、动态性能好、功率密度高等优点[4-5]，在垂直提升系统领域内，由直线电机驱动的无绳提升系统无疑将是最好的选择。

PMLSM垂直提升系统取消了传统曳引提升系统的配重，轿厢动力源全部来自于直线电机，这就要求PMLSM具有足够大的推力密度，然而，现有的PMLSM推力密度较低，仍不能满足实际工业发展的需求，且常规结构的凸极永磁直线同步电机对气隙要求较高，气隙长度小时永磁体有较高的利用率，但气隙长度增大时，漏磁显著增大，电机功率将明显减小[6]。因此，开展大推力PMLSM的结构创新及电磁特性的研究，对于扩展直线电机垂直提升系统的应用范围具有重要意义。

针对现有的直线电机垂直提升系统所存在的电机推力自重比较低的问题，本文提出一种凸极Halbach永磁直线同步电机的设计方案，并对凸铁宽度、高度和永磁体磁化方向对SH-PMLSM单元电机性能的影响进行研究[7]。

1 SH-PMLSM原理及结构设计

1.1 结构原理

常规凸极永磁直线电机结构如图1所示。

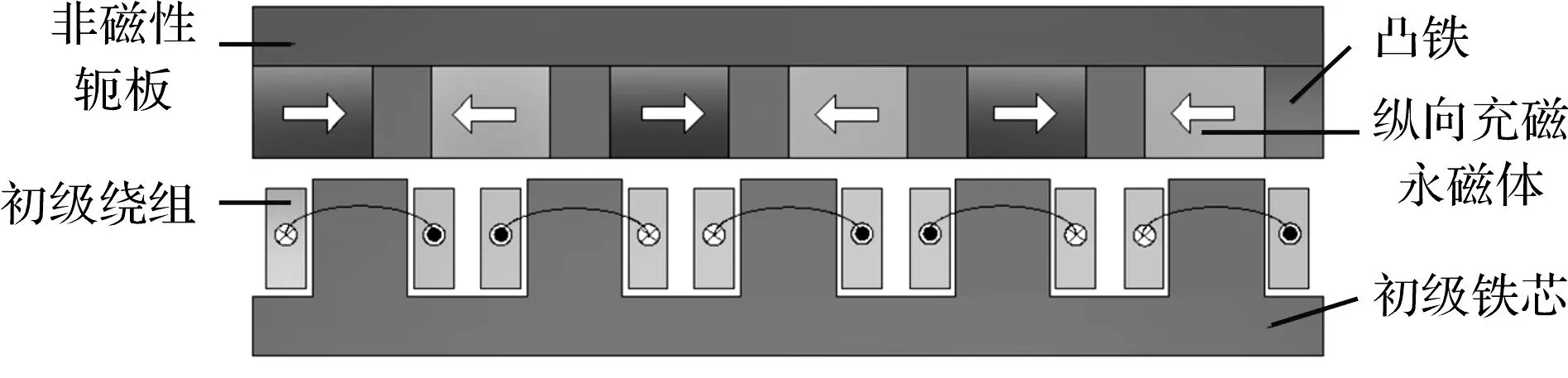
图1 常规凸极永磁直线电机结构

凸极Halbach永磁直线电机如图2所示。

图2 凸极halbach永磁直线电机结构

本文提出的凸极Halbach永磁直线电机为单边电机结构[8],主要分为次级动子和初级定子两大部分，综合了Halbach电机、凸极电机和永磁直线电机的结构和优越性，次级部分由非磁性轭板、永磁体和凸铁构成，次级永磁体的结构是将常规凸极直线电机磁极结构置于Halbach阵列中[9-11]。

有限元仿真磁场分布如图3所示。

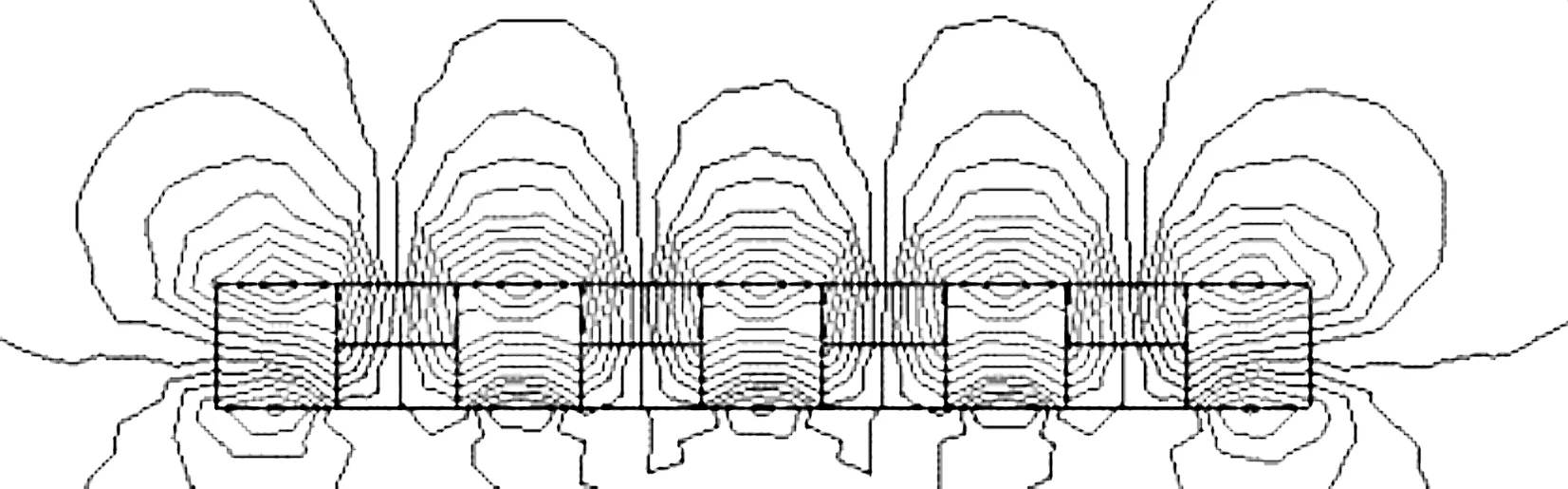
图3 SH-PMLSM磁极永磁体结构磁场分布

由图3可以看出：绝大部分磁场分布在永磁体结构一侧，而另一侧几乎不受磁场影响，这种特殊的磁场分布改善了常规凸极直线电机受气隙长度约束的情况[12]。通过分析，SH-PMLSM在大气隙的工况下，漏磁较少，相应的推力密度较高，可解决常规凸极结构永磁直线电机在提升系统中推力不足的问题。

1.2 初级绕组方案

本文所设计电机采用节距为1的分数槽集中绕组。对于直线电机，初级绕组采用分数槽集中绕组有助于提高绕组的分布系数和槽满率，通过合理的设计可以使分数槽集中绕组节距为1，即每个齿上套一个线圈，线圈端部仅跨过一个槽距，使线圈的总长度和端部伸出长度缩短，从而减少总用铜量，降低铜耗，进而提高电机效率，且端部绕组不会交叠，不用设计相间绝缘[13]。

本研究对电机分数槽绕组进行分析，确定该电机极槽配合方式为16级15槽，绕组系数为0.951，绕组接线如图4所示。

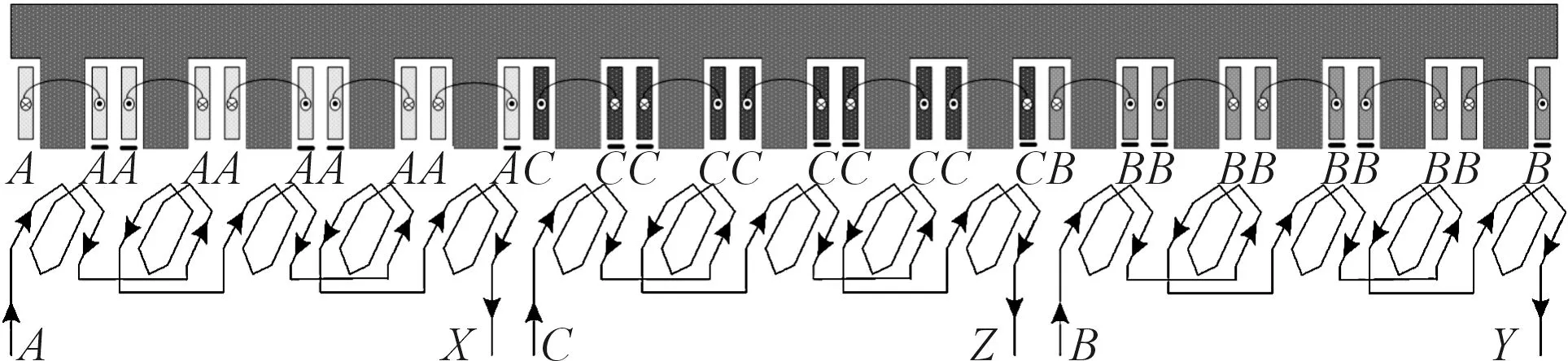
图4 绕组接线示意图

初级每个齿上嵌套一个线圈，相邻齿上线圈反向串联，5个线圈串联构成一相，三相间无重叠绕组[14]。

本研究在旋转电机尺寸关系的基础上，对直线电机主要尺寸之间的关系进行推导，进而确定该电机纵向长度为360 mm，电枢计算长度为70 mm，最后选定该电机所用硅钢为50W470型无取向硅钢，选定永磁体材料为钕铁硼[15]。

2 SH-PMLSM特性分析

基于有限元，本文搭建凸极Halbach永磁直线同步电机单元电机模型，分析其静态特性与稳态特性，并在等永磁体用量、相同的初级和气隙条件下，与隐极式永磁直线电机(S-PMLSM)进行对比分析，研究不同结构参数对SH-PMLSM单元电机性能的影响。

2.1 静态特性分析

15/16级SH-PMLSM结构参数如表1所示。

表1 15/16级SH-PMLSM结构参数

16极15槽凸极Halbach永磁直线电机(SH-PMLSM)次级由Halbach阵列、凸铁极和非磁性轭板构成。电机的磁体结构采取纵向充磁方式，通过两块永磁体之间法向充磁的永磁体将纵向磁场转为法向，电机运行时法向磁场为有效磁场[16]。笔者根据表1结构参数，通过设置无限长的初级理想边界条件，建立16极15槽的单元电机模型如图5所示。

图5 15/16极SH-PMLSM单元电机模型

本研究通过软件仿真给电机模型赋予同步运行速度v=1.035 m/s，求解电机的空载感应电动势E0，空载感应电势(EMF)波形如图6所示。

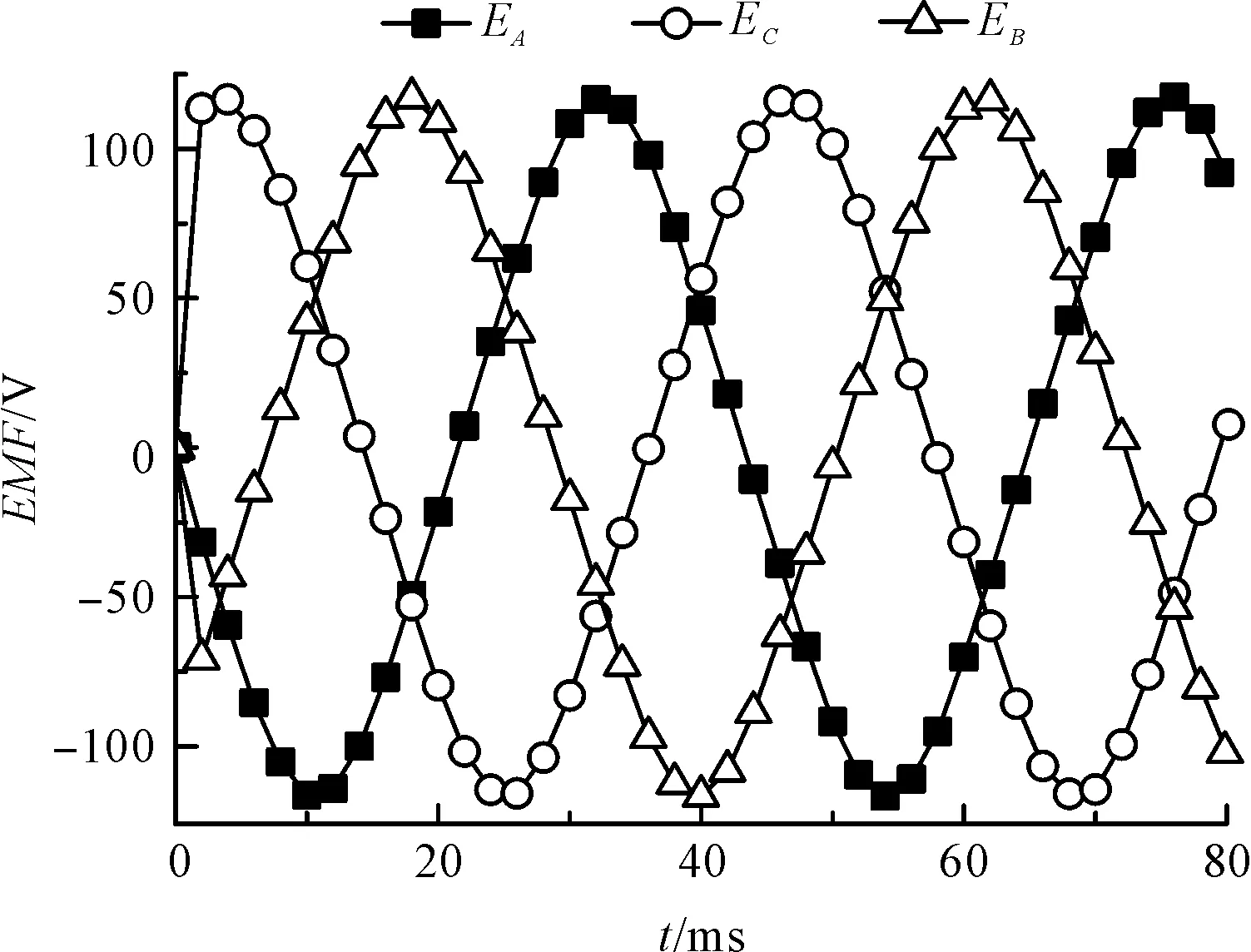
图6 SH-PMLSM三相感应电势

ABC三相空载感应电动势EA、EB、EC幅值一致(有效值为85.9 V)，相位互差120°电角度，正弦度较好，并计算出电机的反电势常数Ke为：

本研究搭建的隐极型永磁直线同步电机单元电机模型如图7所示。

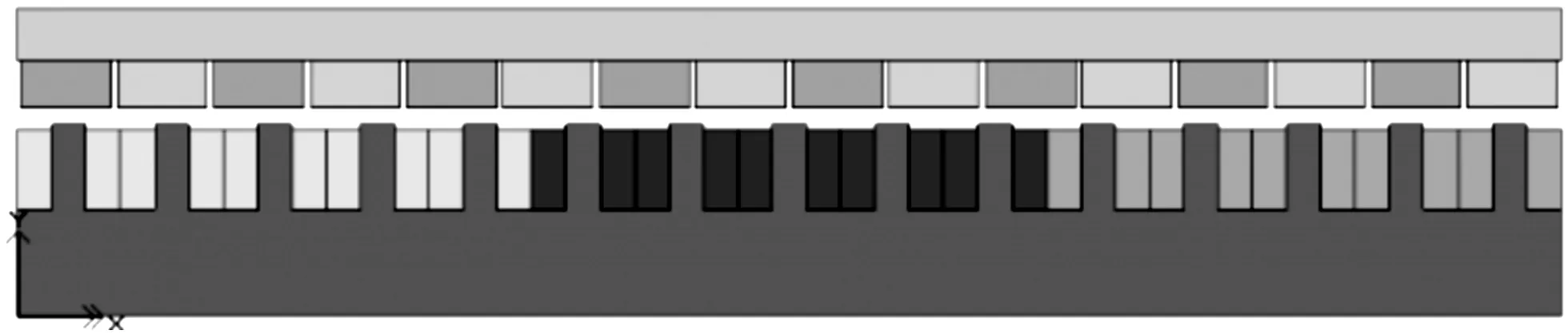
图7 等永磁体用量条件下的S-PMLSM单元电机模型

求解其空载反电势，得到其反电势波形如图8所示。

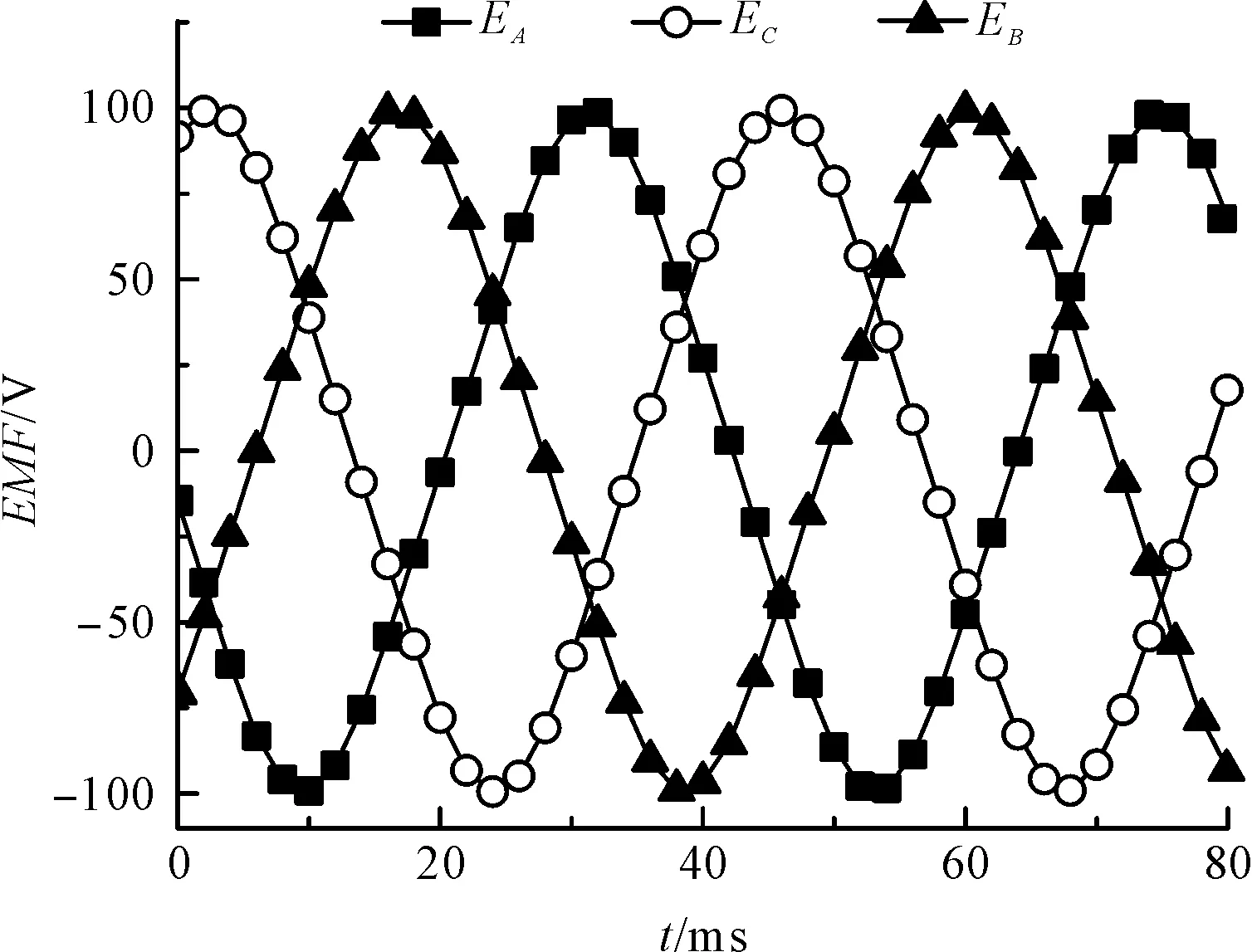
图8 S-PMLSM三相感应电动势

对比SH-PMLSM，结果显示：SH-PMLSM的电势相对提高了15.18%，从而使SH-PMLSM在相对较小的初级电流情况下具有更大对的推力密度。

2.2 稳态特性分析

基于有限元，本研究建立16p15s SH-PMLSM单元电机模型，分别求解在50%、100%、150%负载下的稳态特性，并得出其在不同负载下的推力。

不同负载下的推力曲线如图9所示。

图9 SH-PMLSM不同负载下推力波形

从其推力波形上来看，所设计的SH-PMLSM至少具有1.5倍的过载倍数，并且推力响应较快，但存在一定的推力波动。

在永磁体用量相同、相同的初级结构和气隙条件下，分别对比不同负载角下SH-PMLSM与S-PMLSM推力、电流、功率因数及效率等稳态特性。稳态特性对比结果如表(2～5)所示。

表2 SH-PMLSM与S-PMLSM电机推力特性对比

表3 SH-PMLSM与S-PMLSM单元电机电流特性对比

表4 SH-PMLSM与S-PMLSM单元电机功率因数特性对比

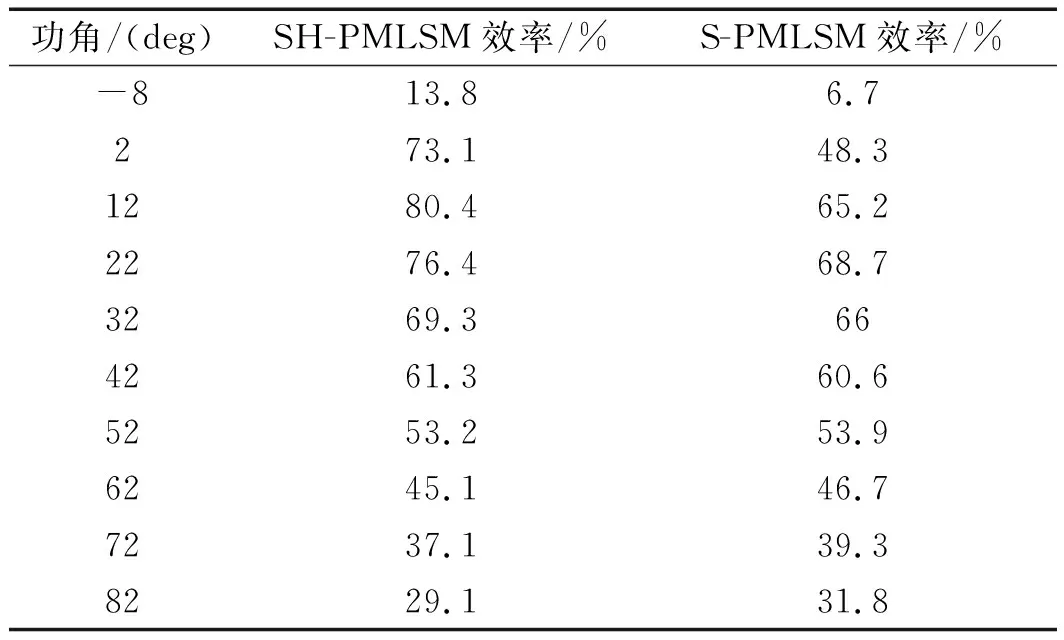
表5 SH-PMLSM与S-PMLSM单元电机效率特性对比

由此可以得出：SH-PMLSM较S-PMLSM在推力、功率因数、电流、效率特性等方面都有较大提高，笔者选取1.5倍过载倍数为额定点，通过分析得出，在额定点附近SH-PMLSM的推力比S-PMLSM提高了约10.61%、电流则减小了约17.34%、功率因数约提高了12.20%、效率约提高了11.71%。

3 不同参数对SH-PMLSM电磁特性的影响

本研究在等永磁体用量前提下，改变SH-PMLSM次级凸铁高度和宽度、次级永磁体磁化方向对单元电机进行仿真，分析其对单元电机推力、电流、功率因数、效率等特性的影响，优化电机的性能。

3.1 改变凸铁高度对电机性能的影响

SH-PMLSM次级永磁体用量不变，本研究改变凸铁高度，仿真得到不同凸铁高度下的电机额定点推力和电流。

不同凸铁高度下的电机额定点推力和电流如表(6，7)所示。

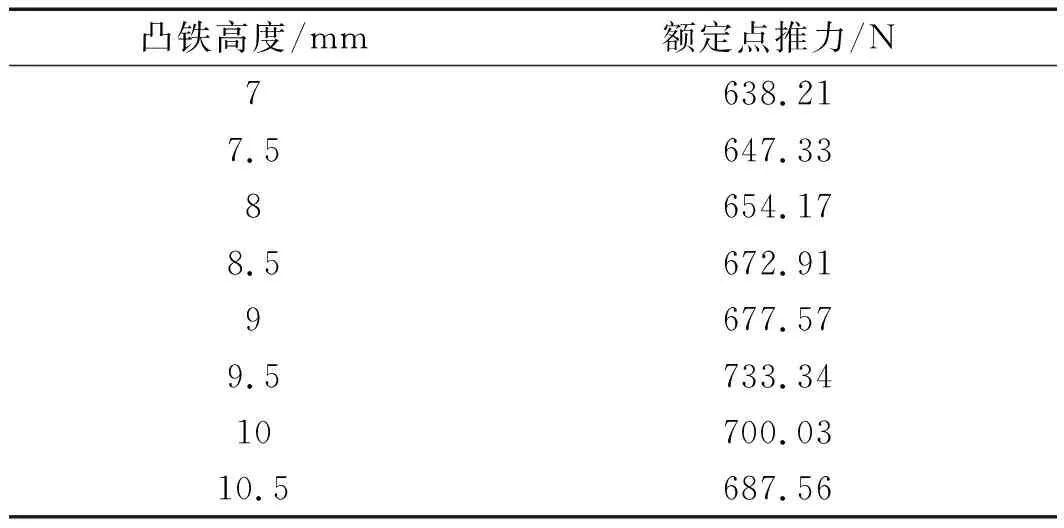
表6 SH-PMLSM不同凸铁高度下的额定点推力

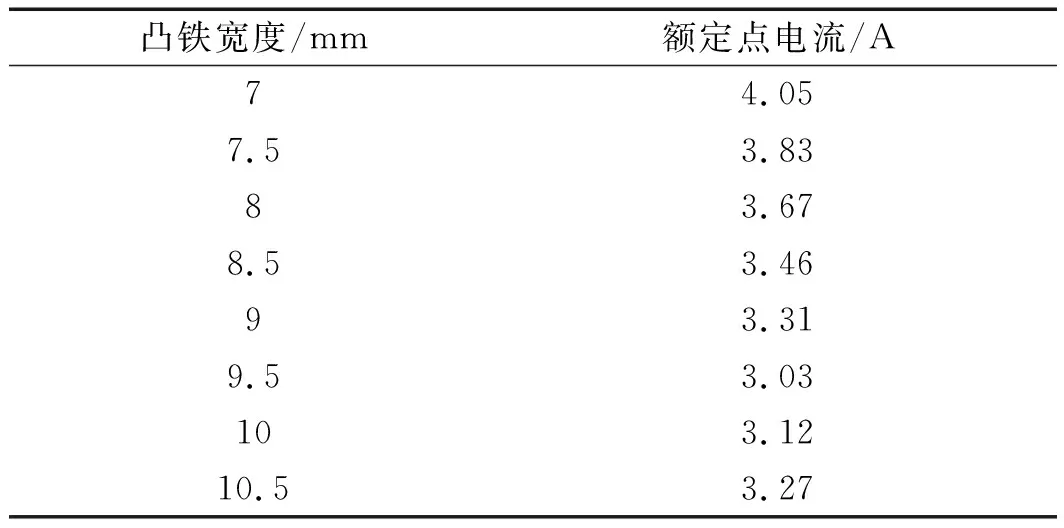
表7 SH-PMLSM不同凸铁高度下的额定点电流

由表(6，7)可以得出：当凸铁高度改变时，SH-PMLSM额定点的推力及电流变化都在9.5 mm处出现了拐点；当电机次级凸铁高度为9.5 mm时，额定点的推力达到最大，而对应的电流则为最小。

3.2 改变凸铁宽度对电机性能的影响

SH-PMLSM等永磁体用量前提下，改变次级凸铁宽度，仿真得到不同凸铁宽度下，单元电机额定点处的推力、推力波动、电流变化情况，结果如表(8～10)所示。

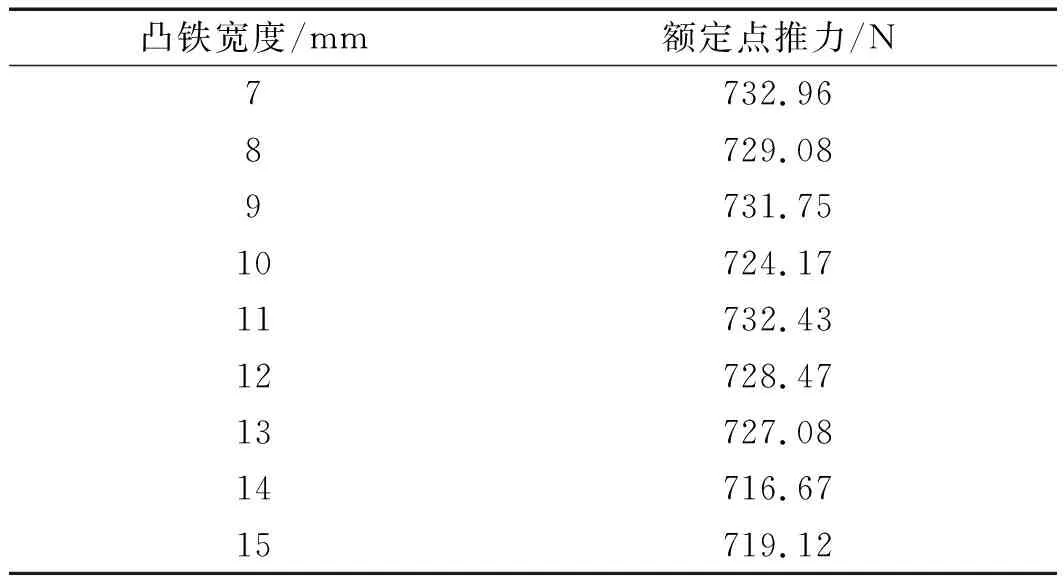
表8 SH-PMLSM不同凸铁宽度下的额定点推力

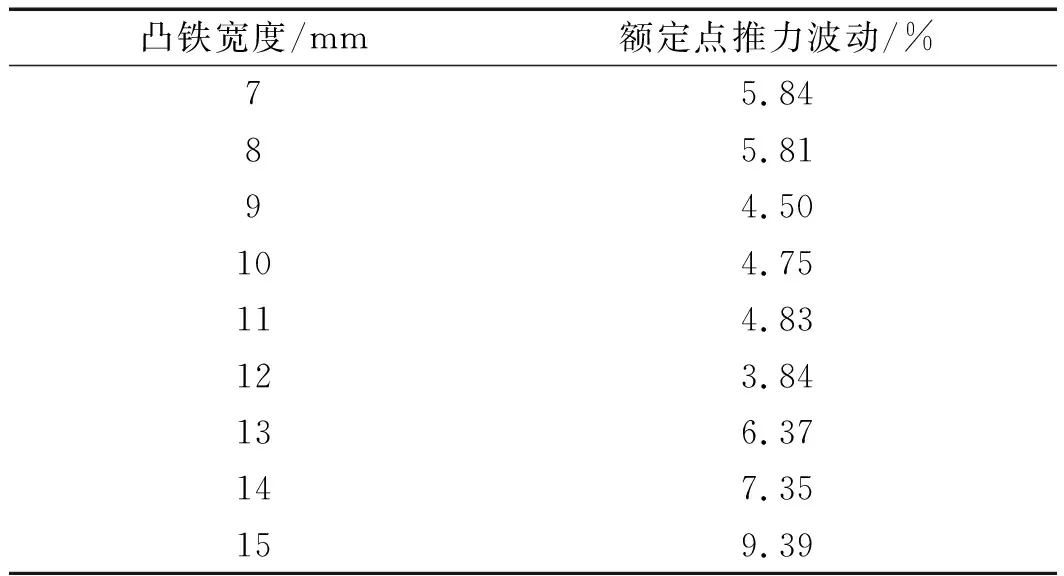
表9 SH-PMLSM不同凸铁宽度下的额定点推力波动

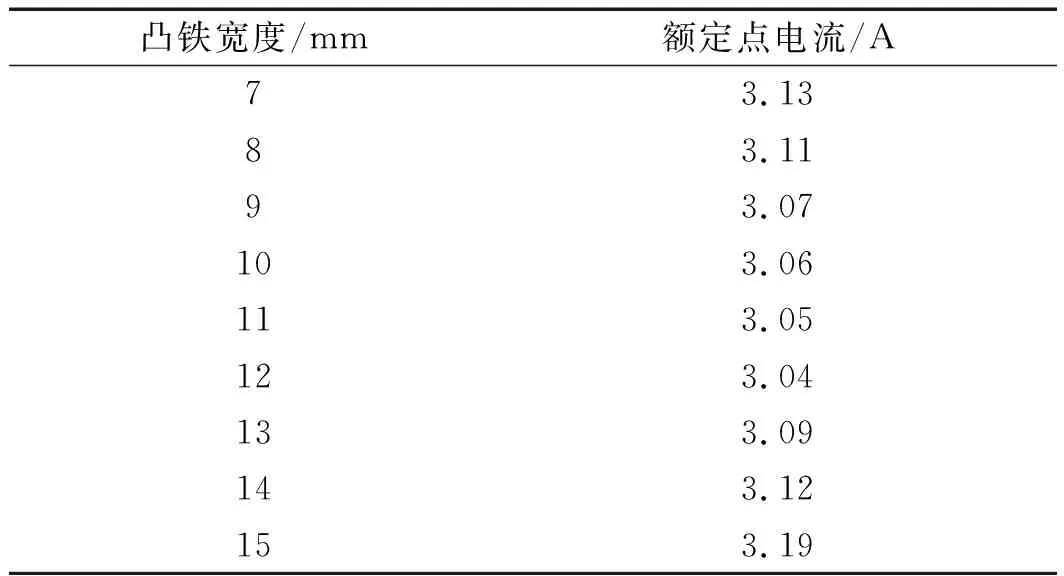
表10 SH-PMLSM不同凸铁宽度下的额定点电流

由以上数据可得出：改变电机次级凸铁宽度对SH-PMLSM推力的影响不大；但结果中推力波动、电流变化则都出现了拐点。综上可得出：当电机凸铁宽度为12 mm时，额定点的推力波动及电流都达到最小值。

3.3 永磁体磁化方向对电机性能的影响

SH-PMLSM单元电机次级磁体结构分为上、下两层：一对极下的磁体排列如图10所示。

图10 一对极下的磁体结构

上层永磁体为Halbach阵列，由两块X方向磁化的永磁体和两块Y方向磁化的永磁体构成；下层一对极分别由两块X方向磁化的永磁体和两块凸铁交替排列组成。

同时改变下层永磁体PM2和PM4的磁化偏转角度(15°、30°、45°、60°)，如图11所示。

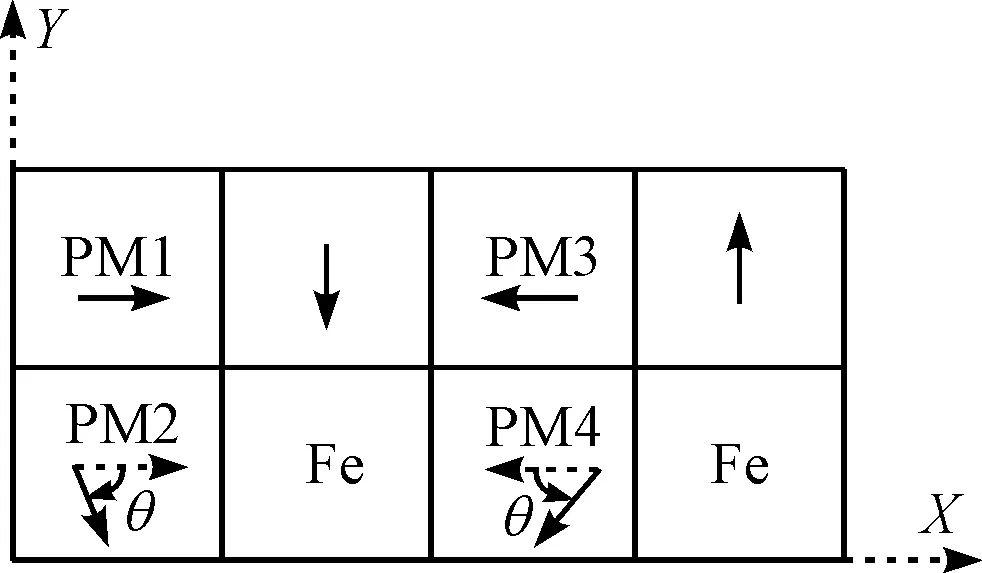
图11 PM2和PM4磁化角度改变

不同磁化方向下电机额定点的推力如表11所示。

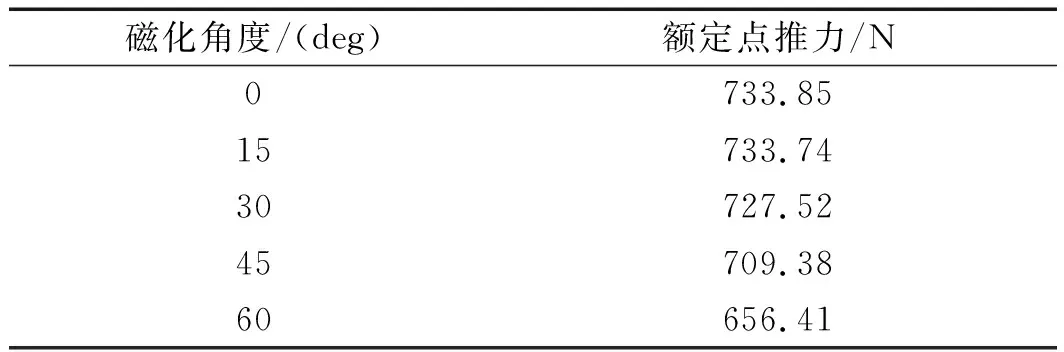
表11 PM2和PM4不同磁化角度下的额定点推力

由表11可知：SH-PMLSM单元电机推力对PM2和PM4磁化方向的变化较为敏感，随着PM2和PM4磁化方向向下偏转，单元电机在额定点处的推力降低较为明显。

本研究改变SH-PMLSM次级上层永磁体PM1和PM3的磁化偏转角度θ，PM1和PM3的磁化方向同时偏转(150、300、450、600)，如图12所示。

图12 改变PM1和PM3磁化角度

SH-PMLSM单元电机额定点推力如表12所示。

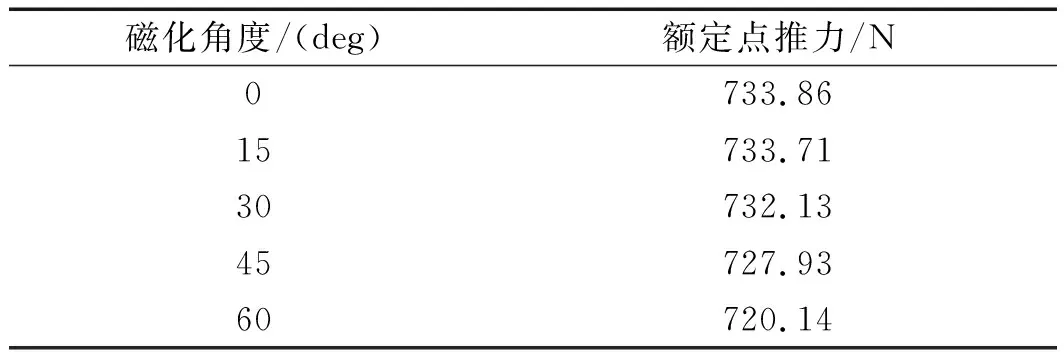
表12 PM1和PM3不同磁化角度下的额定点推力

由此可见：当PM1和PM3磁化方向的偏转角度较小时，变化不明显；偏转角度较大时，变化较为明显；总体而言，随着PM1和PM3磁化方向向下偏转，单元电机额定点推力呈降低趋势。

4 结束语

本文提出并研究了一种凸极Halbach永磁直线同步电机(SH-PMLSM)，分析了电机次级凸极Halbach永磁阵列结构特点和磁场分布；对电机分数槽绕组进行了分析，选定了电机16极15槽的极槽配合方式；确定了SH-PMLSM的主要尺寸；基于有限元建立了SH-PMLSM的单元电机模型，分析了该型电机的静态、稳态特性，以及不同凸铁高度、宽度、永磁体的磁化方向对电机性能的影响。

研究结果表明：由于Halbach阵列良好的磁屏蔽性，SH-PMLSM改善了常规凸极永磁直线电机在提升系统中存在的漏磁较大、推力不足的问题。但该新型电机尚有许多方面有待研究，如推力波动、磁链电感计算、样机制作等。