混合遗传算法在塔吊装载问题中的应用
张 鸽 张 弘李宗亮
(1.西安邮电大学自动化学院 西安 710121)(2.北京建工集团有限责任公司 北京 100055)
1 引言
塔吊以其工作效率高,使用范围广等特点,成为使用最为广泛的建筑工程机械。塔吊资源的调度与运输是建筑项目中不可缺少的环节。目前工地上对塔吊装载物料的分配还处于简单的人工决策阶段,浪费大量时间的同时还经常造成分配不均,从而导致建设项目进度滞后,不得已采取加班保证工期的手段。合理的装载方案不仅可以降低运输成本,而且能够大大提高塔吊的作业效率,有效地提高施工企业的经济效益和竞争力。因此,找到一种合理的塔吊装载方案十分必要。
塔吊的装载问题是一个复杂的工程应用问题,建筑材料的大小、形状、材料是否可以同时装载等都决定了在装载时可以采取的不同策略,也就形成了不同子类别的装载问题。求解装载问题的方法有贪心算法[1]、遗传算法[2]、动态规划算法[3]等,这些算法均能找到问题的最优解,但也均有各自的局限性和缺陷[4]。因此,本文采用一种新的算法—混合遗传算法[5],来求解塔吊装载问题,寻求一种装载总价值最大的解决方法。通过实例验证表明,该混合遗传算法装载总价值大且求解速度、收敛速度快,能够很好地实现物料装载的合理分配。
2 装载问题的数学模型
装载问题的定义:假设某施工现场有n种建筑材料需要用同一塔吊进行装载起吊,其中物料i的重量为wi,该类物料的价值为vi。现在需要求解一种装载方案,寻求对承载总量为W的塔吊,如何运载物料才能使装载的物料总价值最大。
此类装载问题类似于0-1背包问题,即向一个背包中装入该类物品,求解能装入最大价值物品的解决方案。此类问题的求解过程可以看作一系列决策的过程,即决策所给定的物料中哪些应载入塔吊,哪些不能载入塔吊。借助背包问题的基本思想,将本文涉及的问题抽象化,并形式化描述为如下问题:
W>0,wi>0,vi>0(1 ≤i≤n ),要找出另一 n元向量,1表示选用该材料,0表示不选该材料。
由此,塔吊装载问题可以表示为0-1整数规划问题:
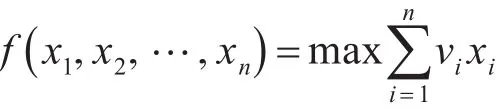
且满足以下两个约束条件:

3 求解装载问题的两种基本算法
3.1 遗传算法求解装载问题
由于装载问题是一个典型的组合最优化问题,遗传算法是解决搜索问题的一种通用算法,它通过模拟自然进化过程搜索到最优解。因此,我们可以将此算法应用于装载问题。遗传算法应用于装载问题时,涉及到约束条件满足下的遗传编码方法,以及选择、交叉、变异操作算子的设计等方面[6]。遗传算法求解塔吊装载问题的基本原理为通过随机方式为物料进行编码,形成初始群体,若载入塔吊,编码为1;不载入塔吊,编码为0。通过适应度函数对每个个体进行数值评价,选出高适应度的个体进行遗传操作,从而形成下一代新的种群。
3.2 贪心算法求解装载问题
常用的贪心准则是价值密度(价值重量比viwi)贪心算法,这种选择准则为从剩余物料中选择可载入塔吊的viwi值最大的物品,这也是最常用的贪心策略[8]。
4 混合遗传算法求解装载问题
4.1 问题描述
简单遗传算法在求解塔吊装载问题的搜索过程中,由于该个体的适应值大大优于当前种群的平均适应值,使进化初期的超常个体可能限制了其他个体进化,根据遗传算法适者生存的原理,使得该个体迅速充满整个种群,种群的多样性大大降低,导致种群的进化停滞,从而出现算法收敛于局部最优解的早熟现象,基于以上问题,本文提出一种将贪心算法与遗传算法相结合的混合遗传算法,应用到塔吊装载问题中,充分利用贪心算法的修正以及遗传算法的择优,不断重复执行选择、杂交和变异,从而得到最优个体,这个个体可能就是装载问题的最优解。
4.2 算法流程图
该混合遗传算法流程图如图1所示。

图1 混合遗传算法流程图
根据塔吊在承载量约束限制之内求解所载物料的最优解和最大总价值。具体步骤如下:
1)基因编码及物料初始化
本文使用等长度的二进制编码对由n个物料xi的值顺序排列构成的装载问题进行遗传编码,编码串中1表示将对应的物料载入塔吊中,0表示不载入。
分别调整纺丝组件压力和改变PE、PA6两组分比例,当纺丝熔体从复合纺丝组件喷丝孔中挤出,达到稳定状态后,剪取喷丝板下约1 m位置的初生丝,用纤维切片器制得纤维截面样品,在双目纤维镜下观察纤维截面形状。继续PE/PA6皮芯型复合纤维FDY纺丝试验,观察纺丝状况变化。
例如“101010”就代表一个解,它表示将第1,3,5号物料载入塔吊中,其他的物料则不载入。
2)编码修复
解决塔吊装载问题的关键是处理好约束条件。我们利用贪心算法的思想对那些不满足约束条件的基因编码串进行修复。其基本思想是优先载入(viwi)较大且 xi=1的物料,直到满足塔吊的承载量约束为止。对于基因编码串中指示应该装入而已经装不下的物料,修改其基因编码串对应的xi为0[9]。这样就可以产生一些新的并且满足塔吊装载问题约束条件的基因编码串。
3)适应度函数
适应度函数是遗传算法进化过程的驱动力,也是进化自然选择的唯一标准[10]。由于对每种物料使用贪心算法修正已保证了不会产生无效的数据,所以在进行物料适应度评价时直接用目标函数值作为适应度函数值,即

4)选择
选择操作的任务就是从父代群体中选取一些个体,遗传到下一代群体[11]。本文采用轮盘赌的方式进行选择[12]。其基本思想是每件物料被选中的概率与其适应度函数值大小成正比[13]。设共有N件物料,物料xi的适应度为 f()xi,则物料 xi的选择概率为

5)交叉
交叉是指把两个父个体的部分结构加以替换重组而产生新的个体[14]。论文采用单点交叉方式,具体操作方法为在基因串中以概率Pc选择一个交叉点,实行交叉时,该点前或后的两个个体的部分结构进行互换,并产生新个体[15]。
为了使求得的解最优且收敛速度快,根据经验本文选用的交叉概率Pc=0.4。
6)变异
变异是指子代基因按小概率(即选择相对较少的个体产生变异,这样即能保证种群的多样性,又不至于过多地丢失父代中有价值的信息)扰动产生的变化[6]。为了求得最优解并且保证种群的多样性,本文中使用一个较小的值如Pm=0.02。
5 实例分析
某施工现场用承载量为2000kg的塔吊装载20件物料,载入的物料不可分割,求使得在塔吊承载量约束限制之内所载物料的最优解和最大总价值。每种物料的重量和价值如表1所示。

表1 物料参数信息表
本文分别用贪心算法、基本遗传算法和基于贪心算法的混合遗传算法来求解塔吊装载问题,3种算法解决装载问题的运行结果如表2所示。算法运行参数设定:交叉概率Pc=0.4,变异概率Pm=0.02,终止进化代数为1000。

表2 3种方法解决装载问题的运行结果比较
从表2看出,采用上述3种方法,在运行参数一定情况下,改进的遗传算法较简单的遗传算法将塔吊的总价值增加了46。进而验证了混合遗传算法在求解塔吊装载问题的可行性。通过程序运行时间的对比,改进后的算法较2种基本算法求解速度更快,验证了混合遗传算法在求解塔吊装载问题的高效性。
基于Matlab软件环境对该装载问题进行了仿真[16],结果如图2所示。(a)和(b)分别为遗传算法和混合遗传算法的仿真图,从图中可以看出,将贪心算法的思想融入到混合遗传算法中,在求解塔吊装载问题时,塔吊的总价值较单一的遗传算法更优,并且求解速度更快。与单一的遗传算法相比,运行速度提高了1/2,相对于贪心算法,运行速度提高了1/5。因此,混合遗传算法相对于贪心算法和基本遗传算法在求解塔吊装载问题上效果更好。

图2 2种算法仿真图
6 结语
塔吊的装载问题一直是建筑行业工程施工的一大难题,是严重影响施工企业的经济效益的一个重要因素。本文应用遗传算法进行优化处理并将贪心算法引入到遗传算法中,避免了在寻优过程中出现局部最优。实例分析表明,在塔吊承载范围内,混合遗传算法实现了对塔吊装载问题的合理分配,且该算法求解速度快,所以,该算法是求解塔吊装载问题的一种有效算法,能有效缓解人工制订塔吊装载物料计划所造成的物料分配不均、浪费时间等现象,提升了塔吊作业效益。

