基于Levy飞行机制的风驱动优化算法
朱祥兵 李垣江,2 王建华 武汉卿
(1.江苏科技大学电子信息学院 镇江 212003)(2.毫米波国家重点实验 南京 210096)
1 引言
风驱动优化(Wind Driven Optimization,WDO)算法是在2010年由Zikri Bayraktar博士等提出的一种基于种群的全局优化算法[1]。该算法对空气质点受力情况进行模拟,研究质点在地球大气层内的运动状况,同时根据牛顿第二定律(F=ma)和理想气体定律(pV=nRT),可以推导求出空气质点的速度和位置更新方程。近几年,风驱动优化算法已经成功应用于许多领域,例如电磁优化领域[2]、图像处理[3]、云资源调度分配[4]、层次规划[5]等。
传统的风驱动算法跟其他智能优化算法一样,容易陷入局部最优极值,特别是在多峰函数优化时,无法从局部最优值中跳出,无法获得理想的全局最优效果。与其他智能算法类似,风驱动算法的改进策略集中在种群的多样性、变异性[6]及寻优策略等方面。文献[7]提出了五种不同的变异机制(小波变异策略、混沌变异策略、非均匀变异策略、高斯变异策略以及柯西变异策略),并与粒子群算法对比分析风驱动优化算法的优化能力,实验结果表明,小波变异风驱动优化(Wind Driven Optimiza⁃tion with Wavelet Mutation,WDOWM)算法具有较强的寻优能力,可有效跳出局部最优,其寻优速率、收敛精度及算法稳定性均优于粒子群优化算法、风驱动优化算法和其他改进算法,但其全局搜索能力仍然有提高的可能。
本文针对上述的风驱动优化算法易陷入局部最优、早熟收敛的问题,在优化过程中有条件的引入 Levy飞行机制[8~9]更新质点位置,提高空气质点的搜索范围和种群多样性,增强其跳出局部最优的能力,从而实现算法的全局优化。
2 风驱动优化算法
2.1 算法介绍
风驱动优化算法是以地球大气中的任一空气质点为研究对象提出的[10]。根据非惯性坐标系中牛顿第二定律并结合理想气体状态方程,可以简化模型得出WDO算法[1]。算法中主要考虑4个力的作用:由高压指向低压的气压梯度力、与气压梯度力发作用的摩擦力、指向地心的重力和地球旋转引起的科氏力[7]。质点的压力值是对空气质点位置的评价,与其他优化算法中的自适应值类似,一般由目标函数迭代计算得到。
设M个空气质点存在于N维中,那么第i个空气质点的位置信息表达式为
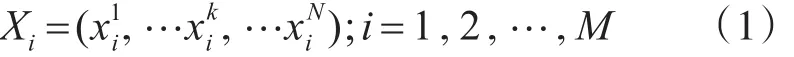


在WDO算法中,空气质点的受力主要由摩擦力,重力,气压梯度力和科氏力组成。式(3)中第一部分代表了空气质点受摩擦力影响,其系数常量a的权重决定对当前质点的速度继承值,根据经验(1-a)不应该超过0.3,正常情况下取[0.8,0.9]。第二部分是重力对质点的影响,是质点对自身当前位置的判断,有助于质点跳出边界和局部最优值,系数g的取值范围[0.6,0.7]。第三部分是气压梯度力对质点的影响,它是一个改进自身位置的过程,初始自己向全局最优位置移动,RT的取值范围在[1,2]。最后一部分是科氏力对质点的影响,将同一指点的其他维度的速度信息借鉴过来,调整自身的速度信息,增强算法的鲁棒性,提高算法性能,系数c的取值范围在0.05~3.6 之间[1]。
2.2 算法过程
WDO算法的实现流程:
1)初始化空气质点的个数和维度,定义最大迭代次数和相关的参数常量,设置搜索边界(位置和速度),设置相应的测试函数。
2)随机初始化各个质点的初始信息(位置和速度),计算初始的压力值并根据压力值的大小升序排列。
3)开始迭代。更新空气质点的速度和位置,计算质点压力值并以升序方式重新排列种群顺序。
4)迭代终止。判断是否满足终止条件,如果不满足就返回步骤3),否则就终止迭代,最后搜索到的最优位置就是最优解。
3 Levy飞行
自然界中很多动物想要在不确定的环境中找到食物,最理想的方式就是采用“Levy飞行”搜索策略,在这种形式的搜索中,短距离的探索性蹦蹦跳跳与偶尔的较长距离行走相间[8]。短距离的行走习惯可以确保动物在对自身周边的环境探索的比较仔细,偶尔的长距离行走可以让动物进入其他环境进行探索,进入更广阔的环境范围。目前,Levy飞行已经被运用于优化领域,比如布谷鸟算法中就用莱维飞行进行位置更新[9]。同时,许多成熟的优化算法也借鉴了Levy飞行机制,改进算法的性能,从而取得了更好的效果[11]。在智能优化算法中使用Levy飞行能扩大搜索范围,增加种群多样性,更容易跳出局部最优值。
使用Levy飞行机制的位置更新方程为[12]
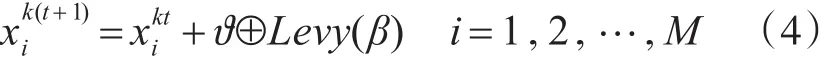
其中:ϑ代表了步长控制量;⊕表示点对点乘法,Levy(β)代表莱维随机搜索路径,同时ϑ和Levy(β)需要满足下列条件:

因为Levy飞行的步长满足一个重尾的概率分布,在用算法编码方面比较复杂,难以实现。所以我们通过Mantegna提出的Mantegna算法来模拟出Levy飞行路径的步长计算公式[13]:

式中:s代表了Levy随机搜索路径Levy(β);β的取值范围在[0,2],通常取 1.5;μ、v是服从式(8)的正态分布随机数:

其中,σμ,σv代表了符合正态分布的标准差,它们的取值满足式(9):
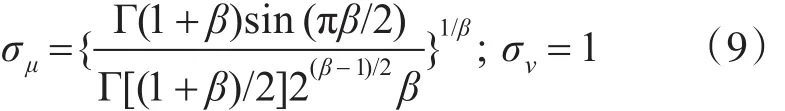
如此就可以模拟出Levy飞行的搜索路径。
4 基于Levy飞行的风驱动优化算法
4.1 算法思想
从WDO算法中,第t次迭代所获得的较好的质点的位置信息可以表示为(i=1,2,…,M),LW⁃DO算法通过一个均匀随机数来确定是否需要Levy飞行进来优化位置信息。
当空气质点在迭代过程中,其速度和位置信息初步更新完毕后,通过随机生成的[0,1]之间的均匀随机数rand来与飞行概率控制变(Levy flight probability,lp)∈[0,1]进行比较,如果小于lp则刚刚更新的位置信息通过式以下飞行公式继续优化:
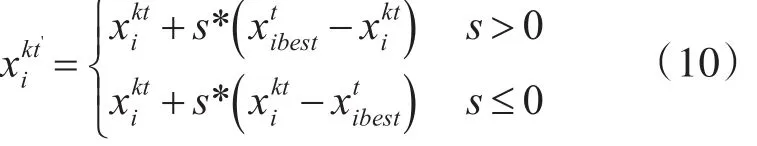
4.2 算法步骤
1)初始化空气质点的个数和维度,定义最大迭代次数和相关的参数常量,设置搜索边界(位置和速度),设置相应的测试函数。
2)随机初始化各个质点的初始信息(位置和速度),计算初始的压力值并根据压力值的大小升序排列。
3)开始迭代,更新空气质点的速度和位置信息,判断速度和位置是否越界,如越界做相应的修正。
4)均匀随机数rand与飞行概率比较lp,如果rand>lp,执行步骤 6),否则执行步骤5)。
5)Levy飞行。通过式(4)开始继续对位置信息进行优化,判断位置是否越界,如越界做相应的修正。计算空气质点的个体压力值并根据压力值的大小做升序排列,更新种群全局最优值glob⁃al_best。
6)迭代终止。判断是否满足终止条件,如果不满足迭代终止。判断是否满足终止条件,如果不满足就返回步骤3),否则就终止迭代,最后搜索到的最优位置就是最优解。
LWDO算法的流程图如图1所示。

图1 基于Levy飞行机制的风驱动优化算法流程图
5 测试仿真
为了测试基于风驱动优化算法(LWDO)的整体性能,将通过Matlab对原始WDO算法、小波变异风驱动优化算法、本文改进算法进行对比分析,从而验证算法的有效性。实验的测试环境建立在In⁃tel(R)Core(TM)i5-2450M CPU@2.50GHz、内存4GB、Windows7操作系统的计算机上,其仿真测试软件为Matlab 2010.b。
如表1所示,本文采用7个比较经典的测试函数。这些测试函数中 f1~f4代表着单峰函数,其中Sphere函数较为简单,用来测试算法的寻优效果;Rosenbrock函数是一个经典且复杂的优化测试函数,其全局最优值位于一条连续的好似长且窄的抛物形态的山谷内,正常较难以找到全局最优值,常用它来测试算法的执行效率;Quadratic和Schwefel函数常被用作检验算法的性能。 f5~f7代表着多峰函数,其中Rastrigin函数Griewank函数类似,都含有较多的局部极小值,常被用来测试算法的寻优效果;Ackley函数提供了一个余弦函数来控制指数函数,局部最优值众多。

表1 测试函数简介
5.1 实验参数设置
在实验过程中,各个算法的种群个数M设置为30,空气质点的维度分别选取10、30,最大的迭代次数设置为200,测试函数的相应搜索范围如表1所示,搜索速度的范围对应于位置搜索范围的百分之一。在标准WDO算法中,常量参数a=0.7,g=0.4,RT=2,c=0.2;LWDO算法中飞行概率主要控制算法前50次迭代过程中寻优曲线的振荡程度,其数值越小,曲线越平稳,在这里取lp=0.2,ϑ0=1,β=1.5;WDOWM算法中,变异概率pm的值与飞行概率相同,取值为0.2;其他参数如ξwm=0.5,gwm=1000[5]。
5.2 实验结果和分析
实验中,3种待测算法的初始化过程相同。采用上述7个测试函数分别对算法的性能进行测试,其独立运行次数为30。最后采用最优压力值(Best Pressure,BP)、平均最优压力值(Mean Best Pressure,MBP)、标准差(Standard Deviation,SD)和平均迭代次数来评价算法的性能。其中BP和MBP体现了算法的寻优精度,SD代表了算法的稳定性,平均迭代次数表示算法的寻优效率。
图2是WDO、LWDO、WDOWM对不同测试函数优化30次的平均最优压力值的曲线,空气质点的维度分别取10和30。表2是对最优压力值、平均最优压力值、标准差的对比结果。表3是对各个算法的迭代次数的统计分析。
根据以上的仿真数据可以总结出以下结论:
1)由表2的最优压力值和平均最优压力值和表3的迭代次数可以看出,对于单峰函数来说,LW⁃DO算法和WDOWM算法比较优秀,在寻优精度上至少领先WDO算法5个数两级,总的来说LWDO的寻优精度比WDOWM好。而且在多峰函数上,LWDO算法的寻优效率远远大于WDOWM和WDO算法,总是领先其他算法20次迭代以上。
2)根据表2中标准差数据可以判断出算法的稳定性能,标准差越小代表稳定性越高,根据表中粗体数据可知:LWDO的算法稳定性最好,WDO算法的稳定性最差。

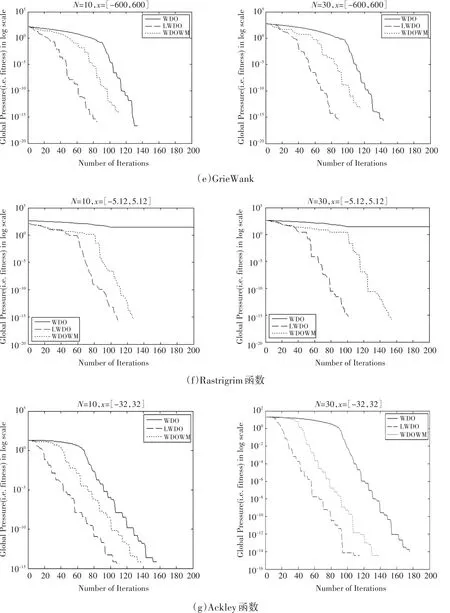
图2 3种不同WDO算法优化测试函数的平均最优压力值曲线
3)图2中,LWDO比其他WDO算法具有更加快速的寻优速率,得到较为满意的结果。在相同迭代次数情况下,对 f1、f4、f5、f6、f7的两种不同维度的仿真结果,实现Levy飞行机制的LWDO算法在任一迭代中都取得较好的结果。
4)由图2可知,在对 f1、f2、f3、f4的计算中,LWDO和WDOWM算法的运算量相近似,比WDO算法的运算量略大,但得到较大寻优精度的提升;而对 f5、f6、f7的优化过程中,LWDO和WDOWM在运算前期比WDO的运算量略大,但其获得理论最优解的速度远超WDO,特别是LWDO只需要将近一半的迭代次数,大大提高了运算速度。
5)结合图2、表2和表3的信息,可以对下面这3种不同算法的寻优性能作出如下判断:LWDO>WDOWM>WDO。无论是从算法的寻优精度、寻优效率和稳定性来看,LWDO算法均有良好的表现,极具应用价值。

表2 仿真数据比较
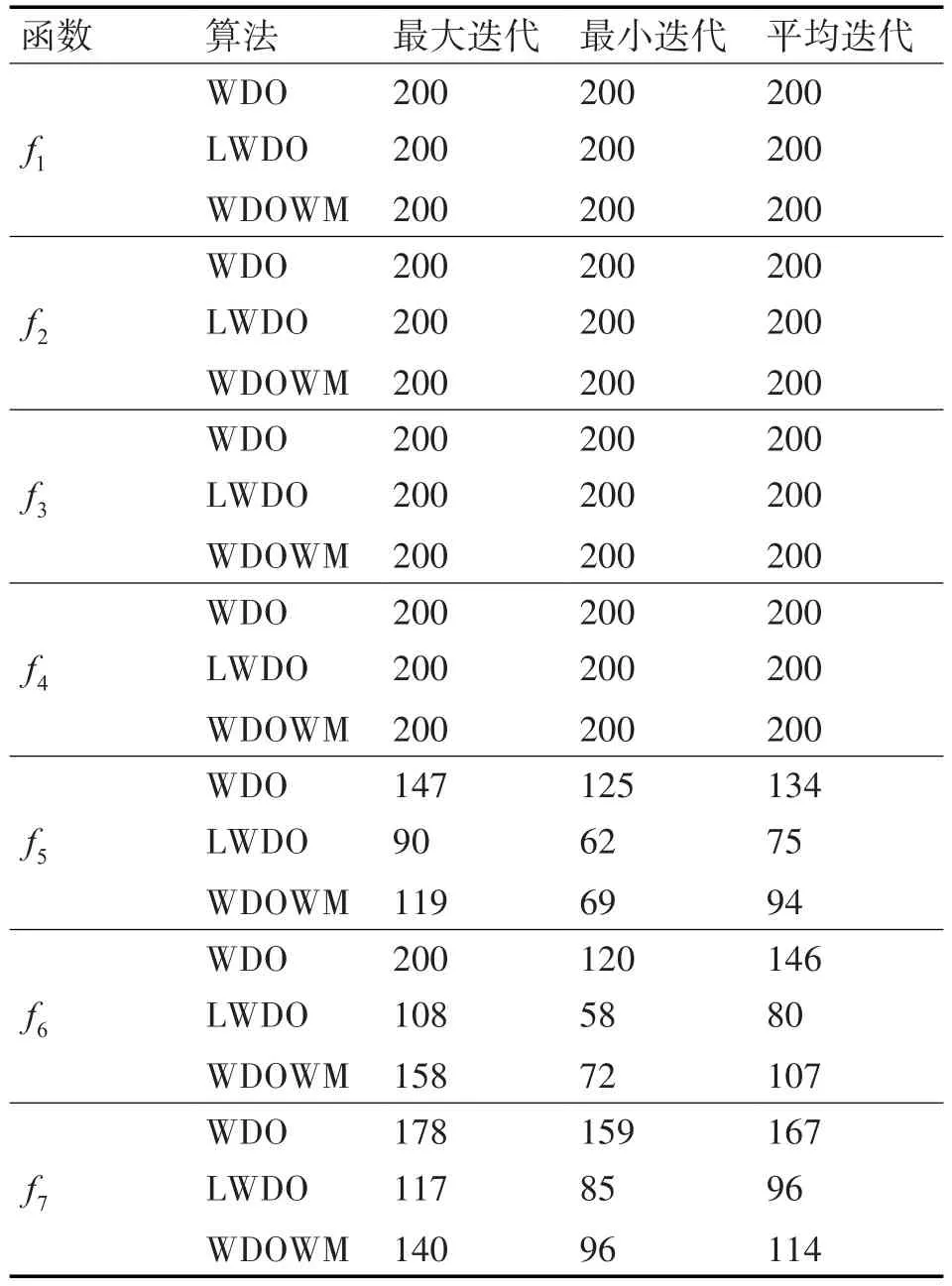
表3 迭代次数比较
6 结语
本文提出一种基于Levy飞行机制的风驱动优化算法(LWDO)。该算法在空气质点初步位置更新完成后通过飞行概率选择性的对质点进行Levy飞行,提高风驱动算法的种群多样性和全局搜索能力。从对标准测试函数的仿真实验可以看出,本文提出的LWDO算法有着较优的收敛精度和收敛速度,不仅提高了算法跳出局部最优的能力,还增强了算法的稳定性,具有较好的应用价值。

