利用落点坐标与运动矢量的脱靶量计算方法

魏 超 黄晓冬

（中国人民解放军92124部队 大连 116023）

1 引言

脱靶量是评价飞行器轨迹精度的一项关键指标，高精度脱靶量计算目前仍然是飞行器攻击地面目标精度考核需要解决的一个难题［1］。脱靶量测量和处理的一个常用方法是光学交会法［2～3］，即用两台以上的光学测量设备获得飞行器攻击目标时飞行器和靶的测角数据，然后按照多站交会法［4～7］计算飞行器和靶的位置坐标，两者作差即可得到脱靶量，而在实际试验时，受光测设备布站地理条件限制和天气状况影响，往往难以达到交会解算的条件。地面接收站能够接收飞行器在空中飞行时的导航数据，对导航数据进行处理可以获得飞行器轨迹参数，求解飞行器轨迹与被攻击目标面的交点也可获得脱靶量。但是实际工况下，受山体、建筑物等遮挡或其它因素影响，造成导航数据在着陆前几秒常发生中断，一般通过将飞行器轨迹外推至目标平面获得脱靶量，其计算精度受导航数据误差的影响很大［8］。

考虑飞行器穿过目标平面后触地形成落点痕迹，试验后对落点进行测量，能够获得该点的大地坐标，由飞行器的导航数据可获取飞行轨迹的倾角、偏角，从而确定了飞行器的来袭方向，从落点中心出发，依据飞行器的运动矢量反向推算飞行器轨迹与攻击目标面的交点，也可获得脱靶量。本文基于这一思想提出了利用落点坐标与运动矢量的脱靶量计算方法，并进行了理论分析和实测计算。

2 脱靶量计算

如图1所示，平面ABCD为目标面，目标中心为O点，飞行器穿过目标面在地面A‘BCD’平面落地形成坑痕，中心点为G，飞行器穿过目标面的点T称为中靶点，EW和SN分别为目标面内过目标中心的东西向和南北向。脱靶量定义为有序数对(r,θ)，其中，r为中靶点T与目标中心O的距离，称之为脱靶量半径，θ为OT与SN的夹角，称之为脱靶量偏向［9］。对导航数据进行处理，得到飞行器轨迹在发射系下的轨迹倾角和偏角，从而可以确定飞行器的入射方向，飞行器最终攻击目标短时间阶段可认为其方向保持不变，以中心G为起始点，根据飞行器飞行的反方向，利用飞行器运动矢量方程逆向推导，求解飞行器轨迹与目标面的交点T，进而可获得脱靶量(r,θ)。

飞行器轨迹倾角λ和偏角σ定义为［10］

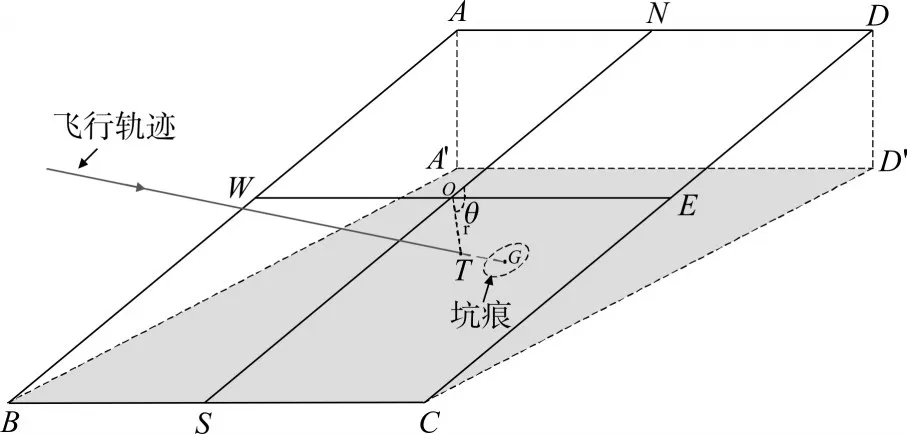
图1 脱靶量示意图

其 中 ，(x˙f,y˙f,z˙f) 为 飞 行 器 在 发 射 系 下 的 速 度 ，，则飞行器在发射系下的运动矢量为

Lf在地心系下的矢量记L，则有

其中，M为发射系到地心系的旋转矩阵［11］：

Bf、Lf、ξf、ηf、Af分别为发射点的纬度、经度、垂线偏差子午分量、垂线偏差卯酉分量、天文射击 方 位 角 ， γf=arcsin{sin[ηfsec(Bf+ξf)]sin(Bf+ξf)}。

验前测量目标面的四个顶点A、B、C、D以及目标中心O的大地坐标，验后测量中心点G的大地坐标。目标中心坐标记为Xo=(xo,yo,zo)T，目标面四顶点A、B、C、D和目标中心O近似在一个平面上，我们任选A、B、C、D中的两个点和目标中心确定目标平面，例如选取O、C、D三个点确定目标平面，C、D两点的坐标分别记为 Xc=(xc,yc,zc)T和Xd=(xd,yd,zd)T，目标平面的单位法线矢量记为n=(nx,ny,nz)T，则有

中靶点T的坐标记为 Xt=(xt,yt,zt)T，由于 Xt位于目标平面上，Xt满足关系式

地心系下的落点坐标记为Xg=(xg,yg,zg)T，根据飞行器的运动矢量L和落点坐标Xg得到关系式

其中，d为落点到中靶点的距离，联合式（2）、（3）和（4）求解中靶点坐标 Xt，可得

获得中靶点坐标 Xt后，脱靶量半径为r=||Xt-Xo||。

目标中心O的经度记为Lo，过目标中心O的大地子午面的单位法线矢量为u=(-sinLo,cosLo,0)T，-⇀----SN和-⇀----WE的单位方向矢量记为 p和 q，则有 p=n×u/||n×u||，q=p×n，令Lr=(Xt-Xo)/r，则Lr为单位向量，其方向从目标中心O指向中靶点T，这样脱靶量偏向的表达式为

3 脱靶量理论精度计算

影响脱靶量计算精度的主要因素是飞行器轨迹倾角偏角误差和落点坐标测量误差，本文主要分析这两个因素对脱靶量半径计算精度的影响［12］。在飞行器轨迹倾角误差dλ偏角误差dσ作用下，脱靶量半径误差dr为

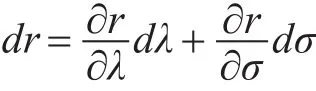
计算 dr需求解 ∂r/∂λ和 ∂r/∂σ ，根据求导法则，有

上式等号右边各项的计算如下

其中，I为3×3的单位矩阵，由式（3）和式（4）得

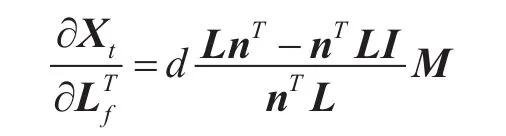
令Lλ=(-sinλ cosλ 0)T，Lσ=(-sinσcosλ-sinσsinλ-cosσ)T，Lλ和 Lσ为单位向量，由式（1）得

设飞行器运动矢量与目标面夹角为α，Lr与L的夹角为 β，则有sinα=nTL，cosβ=LTrL，于是

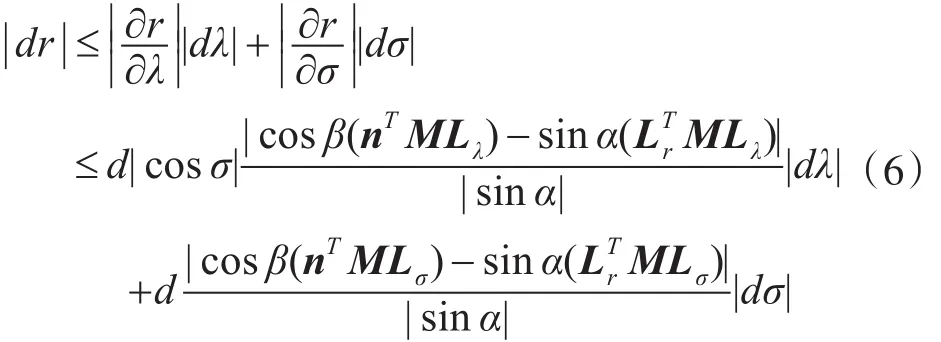
由式（6）可以计算飞行器轨迹倾角偏角误差影响下的脱靶量半径的理论精度。因为M为正交矩阵 ，有，另外，|cosβ|≤|cosα|，由式（6）可得

其中，f为落点中心到目标面的距离，可用上式对脱靶量半径误差的上限进行粗略估计。

下面分析落点坐标误差对脱靶量偏差的影响：

可用上式计算落点坐标误差影响下的脱靶量半径的理论精度。根据式（8）得

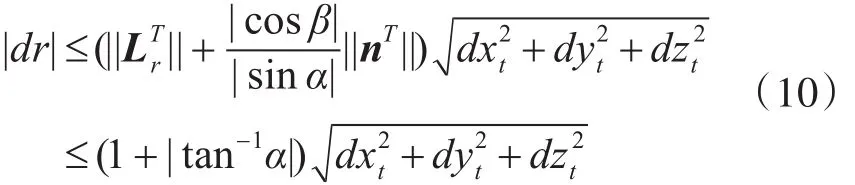
由上式可对脱靶量半径误差的上限进行粗略估计。

4 计算结果及分析

某次飞行器攻击地面目标试验后，对飞行器下传的导航数据进行处理，获取飞行器轨迹的倾角和偏角，人员对地面中心点进行大地测量，获得中心点的大地坐标。依据飞行器轨迹倾角偏角和中心点的大地坐标计算脱靶量，将其与导航数据目标面交会法计算脱靶量的结果作比较，脱靶量半径相差0.404m，脱靶量方位相差0.924°，表明脱靶量计算结果准确可靠。

飞行器轨迹倾角偏角精度取为1°，由式（6）计算飞行器轨迹倾角偏角误差影响下的脱靶量半径的理论精度为0.167m，由式（7）计算的粗略精度为0.420m，飞行器轨迹倾角误差dλ和偏角误差dσ分别在［-1°，1°］变化，采用数值法计算脱靶量半径误差，脱靶量半径误差随飞行器轨迹倾角和偏角误差的变化情况如图2所示，误差最大值为0.165m，接近于理论精度。落点坐标测量精度取为0.2m，由式（9）计算落点坐标误差影响下的脱靶量半径的理论精度为0.353m，由式（10）计算的粗略精度为0.670m，落点坐标误差dxt,dyt,dzt分别在［-0.2m，0.2m］变化，脱靶量半径误差的变化情况如图3所示，误差最大值为0.352，接近于理论精度。

图2 脱靶量半径误差随飞行器轨迹倾角偏角误差的变化

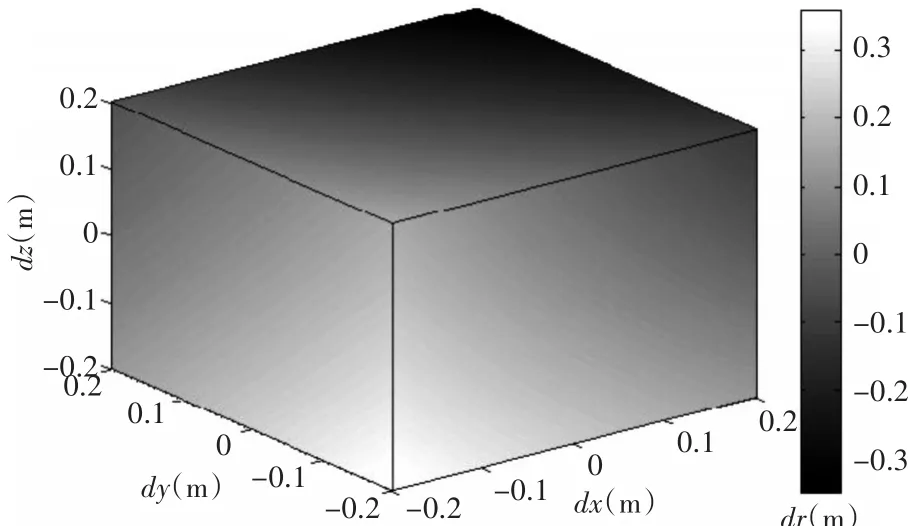
图3 脱靶量半径误差随落点坐标误差的变化

5 结语

文中针对飞行器攻击地面目标试验的脱靶量计算问题，提出了一种利用飞行器运动矢量和落点大地测量坐标计算脱靶量的新方法。该方法依据落点的大地坐标和飞行器最终的运动矢量确定飞行器轨迹，通过求解该轨迹与目标面的交点坐标获得脱靶量。给出了飞行器轨迹倾角、偏角误差和落点坐标测量误差影响下的脱靶量理论精度的计算公式。计算结果证明，脱靶量计算准确可靠，理论精度接近于数值法获得的精度结果，理论精度能够为脱靶量计算精度评定提供可靠的依据。