考虑需求预测误差的PPP项目多目标担保兑付策略研究

， ， ，

(1.华北电力大学 可再生能源学院,北京 102206; 2.华北电力大学 经济管理学院,北京 102206)

1 引言

公私合作(public-private partnership，PPP)模式能够较好地缓解基础设施高速增长所造成的政府财政预算不足问题，近年来在我国得到了快速发展。但由于合作模式的复杂性，PPP项目暴露出了比其他工程项目更高的风险[1]，需求不足风险是PPP项目运营期间所面临的最主要风险之一[2,3]。针对该风险，可通过特许期调整[4～6]、产品价格调整[7,8]或政府担保和补偿机制[9,10]，实现政府部门与私营机构之间收益和风险的动态均衡。但是，特许期调整谈判和监管的成本较高[11]，且忽略了运营资金约束问题使得其应用受限[12]；单一价格调整补偿模式需要考虑公众承受能力约束，补偿效果有限[13]；更常见的方式是针对项目运营过程中的需求不足风险设置担保条款以实现有效吸引私营机构的目的[2,14]。

最低收入担保(minimum revenue guarantee，MRG)是PPP项目中有效应对需求不足风险的常见风险分担机制[3]。但在需求不足情形下，政府方提供的最小收益担保将转变为政府或有债务，推高财政风险。针对上述问题，可通过制定合理的MRG目标，或提高地方政府财政预算管理能力的方式有效应对[15]。例如吴孝灵等[16]基于Stackelberg博弈对政府补偿机制最优设计进行了讨论；Carbonara等[17]提出在确定担保金额时应考虑其产生的或有债务的期望现值限制；谭志加等[18]基于双目标规划模型对收费价格和政府补贴政策的Pareto有效选择问题进行了研究；高颖等[19]针对需求不足风险发生后政府方如何通过需求量补偿机制实现私营机构收益和消费者剩余的帕累托改进进行了研究；刘婷等[3]提出了最低收入担保机制设计原则，并对收入阈值的设计进行了研究等。但上述研究主要集中于如何制定合理的MRG目标，而没有对项目运营期间存在的MRG偿付风险进行深入的研究，值得注意的是，由于受到公众购买能力、地方偿债能力和其他客观因素的影响，前期签订的MRG目标无法得到履行甚至导致项目失败的例子不乏少见[20]，但目前针对财政或有债务进行准确预测和优化支付策略以提高政府财政预算管理能力的研究鲜见[15]。

因此，建立科学合理的量化预测模型，对PPP项目或有债务引起的担保兑付策略进行优化，从而提高预算资金的使用效率和担保兑付率，具有非常重要的现实意义。实践中，由于未来的需求量具有不确定性[12]，需求预测误差被认为是影响收益测算的最重要影响因素[2]。因此，本文在考虑价格调整补偿的基础上，将表征违约风险的担保兑付保证率最高和表征预算资金使用效率的预测兑付额年序列现值总额最低作为多目标函数，构建了PPP项目多目标担保兑付模型(MGP模型)；针对需求预测误差具有模糊性的特征，将担保兑付策略视为模糊事件，引入模糊数学可信性测度对担保兑付保证率这一模糊风险进行量化，并结合遗传算法收敛速度快、求解性能佳的优势，将遗传算法和可信性理论耦合，进一步提出了可信性遗传算法对MGP模型进行求解，为PPP项目担保造成的财政或有债务逐年预测提供量化依据。

2 问题描述和研究假设

2.1 问题描述

本文主要研究政府方提供最低收益担保(MRG)模式下，PPP项目需求不足风险发生时政府方的最优担保兑付策略[3]。实践中，担保兑付策略通常和价格调整补偿措施组合使用，如图1所示。

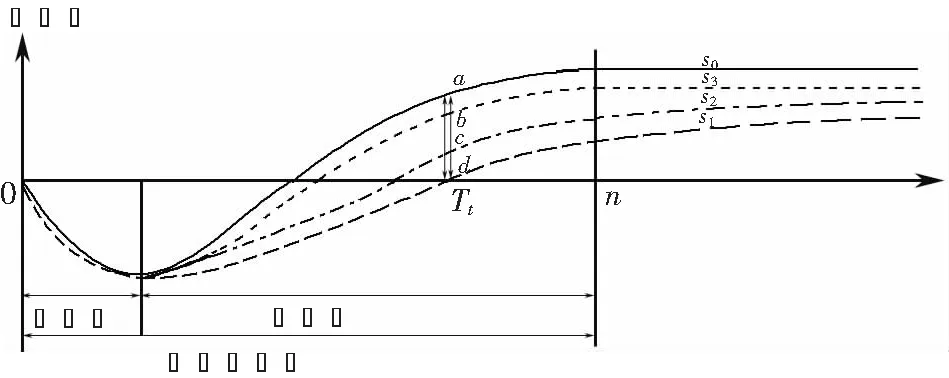
图1 考虑价格调整的担保兑付示意

图中，S0为MRG曲线，S1为未考虑价格调整的实际/预测收益曲线，S2和S3为考虑不同价格调整方案的实际/预测收益曲线，n为特许期年限。按照担保合约，政府方需在每年年末时点(T1,T2,…,Tn)对MRG曲线和实际收益曲线之间的差额进行补偿。以某年末时点Tt(t∈[1,n])为例，假设不考虑价格调整，则政府应兑付的担保金额如图中S0曲线上a点和S1曲线间上d点间差值所示。假设结合价格调整进行补偿，以调价方案1为例，对应收益曲线为S3，此时政府方需兑付的担保金额如图中S0曲线上a点和S3曲线间上b点间差值所示，其余部分通过价格调整的方式得到补偿。此时，在MRG模式下，可提出满足MRG目标的政府担保兑付策略表达式如下

S(t)=Z(P(t),E(t),C(t),Y(t))

(1)

其中S(t)表示预测兑付额年序列，P(t)表示价格调整年序列，E(t)表示项目最小担保收益年序列，C(t)表示成本年序列，Y(t)表示项目实际需求量年序列。

由上述内容可知，预测兑付额年序列现值总额越小，则政府方的预算资金使用效率越高；同时，尽管在运营期内会基于已有实际数据对预测兑付额年序列进行不断更新和修正，误差仍不能完全避免，需要通过担保兑现保证率对预测兑付额年序列的可靠性进行描述。由于在既定价格调整策略下，不同政府担保兑付策略均对应有唯一满足MRG目标年序列的保证率和预测兑付额年序列现值总额，因此，在给定价格调整措施的前提下，可将担保兑现保证率最高和预测兑付额年序列现值总额最低作为多目标函数，对多目标担保兑付策略进行寻优。

2.2 研究假设

为更清晰地对模型进行说明，本文的分析基于以下原则性的假设：

(1)假定项目在全运营周期中具有排它性，不考虑价格弹性对需求量的影响；同时，暂不考虑突发性事件导致项目中止的情况。

(2)按照风险分担原则，运营风险由私营机构承担[1]，因此，假定可参考行业平均成本将预期成本序列C(t)设置为固定数值，即不考虑实际成本风险对收益确认影响。

(3)假定不考虑价格调整审批风险，并假定价格调整序列的调价周期为R年，价格调整幅度为每R年上涨h%，不失一般性，即可认为Tt时点次年起调价格对应有唯一价格调整序列。

3 考虑需求预测误差的PPP项目多目标担保兑付模型(MGP模型)

3.1 模型建立

3.1.1 目标函数

对于不同的担保兑付策略，其预测兑付额年序列现值总额和担保兑付保证率也各不相同，显然，保证率越高，要求的预测兑付额年序列现值总额越高，反之亦然。故两个目标之间存在着矛盾冲突，因此MGP模型目标函数为价格调整序列已知的情况下，寻求最优担保兑付策略，使其满足最低收益担保(MRG)目标年序列的保证率最大，同时满足政府担保兑付策略现值总额最小，可建立目标函数如下

(2)

其中f1为在特许期内满足MRG目标年序列的保证率，Tcg为在特许期内，当前担保兑付策略年序列满足MRG目标年序列的年数，Ttotal为特许期年数；f2为预测兑付额年序列现值总额，St为第t年预测兑付额现值，n为特许期年限。

由前述可知，Tcg是关于价格调整序列P(t)，最小收益担保序列E(t)，成本序列C(t)，政府担保兑付策略S(t)以及需求量预测误差序列ε(t)的函数，即

(3)

其中

gc(f(P(t),E(t),C(t),S(t),ε(t),n))

表示如果该年政府担保兑付策略可以满足最小担保收益，则记为1，否则记为0。f(P(t),E(t),C(t),S(t),ε(t),n)表示该年政府担保兑付策略预测兑付额与实际应兑付额的差值。

3.1.2 约束条件

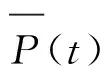
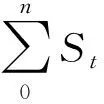
(4)

Stotal为政府接受的预测兑付额年序列现值总额上限，即该项目财政意愿授权支付额度上限。

3.2 基于可信性遗传算法的模型求解

3.2.1 可信性理论

(5)

根据可信性理论，一个模糊事件的可信性定义为可能性和必要性的平均值，当模糊事件可信性为1时，则事件必然成立，而可信性为0时则必然不发生。由于可信性理论修正了传统模糊数学隶属度混乱的问题，通过可信性测度能够准确描述模糊事件的可信程度，其应用已逐步从基础数学扩展到了其他领域[23]。

3.2.2 遗传算法

遗传算法(genetic algorithm)是美国霍兰德教授依据生物进化机制所提出的一种智能算法，基于“物竞天择，适者生存”的法则，通过个体之间的繁衍生息，不断更替进化，得到最优个体。遗传算法基本流程可以简述如下：初始化U个个体，每个个体代表一个决策策略，策略中每个解称为基因，其表达式为X=(x1,x2,…,xu)，其中X为个体，x为个体上的基因，u为决策策略中的维数；确定适应度函数(通常为目标函数)，通过适应度对个体进行排序，将适应度较好的个体保存到下一代，之后通过交叉变异遗传操作来对上述个体进行更新，其中交叉指以一定概率将若干个体进行基因互换，变异指以一定概率将个体基因改变，从而实现更新个体的目的，之后通过不断地循环迭代，输出最终个体。

3.2.3 可信性遗传算法

由于人为认知能力和客观限制，需求预测误差不可避免，并具有一定的模糊性，因此，担保兑付策略的决策可视为模糊事件。根据可信性理论，可信性测度可以用于准确描述模糊事件的可信程度，并且能够有效避免概率论中存在的抽样误差、抽样冗余等问题，故本文采用可信性这一概念来表征目标中的担保兑付保证率，实现模糊风险的量化。在此，担保兑付策略满足最小担保收益的可信性表示为

maxf1=Cr(f(P(t),E(t),C(t),S(t),ε(t),n)≥0)

(6)

考虑到既定可信性要求下可能存在多个担保兑付策略，由于决策变量需要满足既可使得预测兑付额年序列现值总额最小又拥有较高的可信性，每一目标均存在着寻优问题，故实际上是多目标优化问题。遗传算法是一种智能优化算法，能够有效快捷地通过选择、交叉、变异等遗传操作不断对个体适应度进行更新替代，最终输出非劣解集，因此，本文将可信性理论与遗传算法结合，提出可信性遗传算法的模型求解方法，进而得到不同价格下的可信性-担保兑付策略非劣解集，求解步骤如下：

第1步确定特许期期限为n年，计划收益系列值(B1,B2,…,Bn)，最新预测需求量(y01,y02,…,y0n)，确定产品定价取值空间[Pmin,Pmax]，并均匀生成N1个起调定价(P1,P2,…,PN1)，初始化总迭代次数为N2。

第2步初始化N个种群个体(S1,S2,…,SN)，其中某一个体Sj=(sj1,sj2,…,sjn),j∈[1,N]代表在特许期内政府担保兑付系列值；根据预测需求量误差确定隶属度函数μ(x)，本文隶属度函数采用柯西分布函数。

第3步对于某一起始定价Pi，均匀生成误差系列值(ε1,ε2,…,εm)，得到可能的实际需求量系列，并计算得到每一误差系列下的收益差值(g1,g2,…,gn)。

第4步计算每一误差对应的隶属度值，并记vk=μ(u1k)∧μ(u2k)∧…μ(unk)，计算当前担保兑付策略下的可信性。

(7)

其中f(ε)≥0表示当前担保兑付策略满足担保兑付需求；并计算得到当前担保兑付策略下预测兑付额年序列现值总额Stotal。

第5步对每个个体所对应的预测兑付额年序列现值总额和可信性进行非支配排序，采用精英保留策略将N3个个体保留到下一代。

第6步采用交叉变异遗传操作对上述个体进行更新，交叉公式为

(8)

其中(S1,S2,…,SK)为从种群中随机挑选的K个个体，且Σak=1；变异为对某一种群个体上的基因进行重新生成，通过交叉和变异共得到N4个种群个体。

第7步检验是否达到迭代次数，若是，转到第8步，若否，则转到第3步。

第8步检验是否遍历所有起调价格，若是则转到第9步，若否，则转第1步。

第9步输出不同起调价格、不同担保兑付策略下的可信性和预测兑付额年序列现值总额。 其总体计算流程如图2所示。

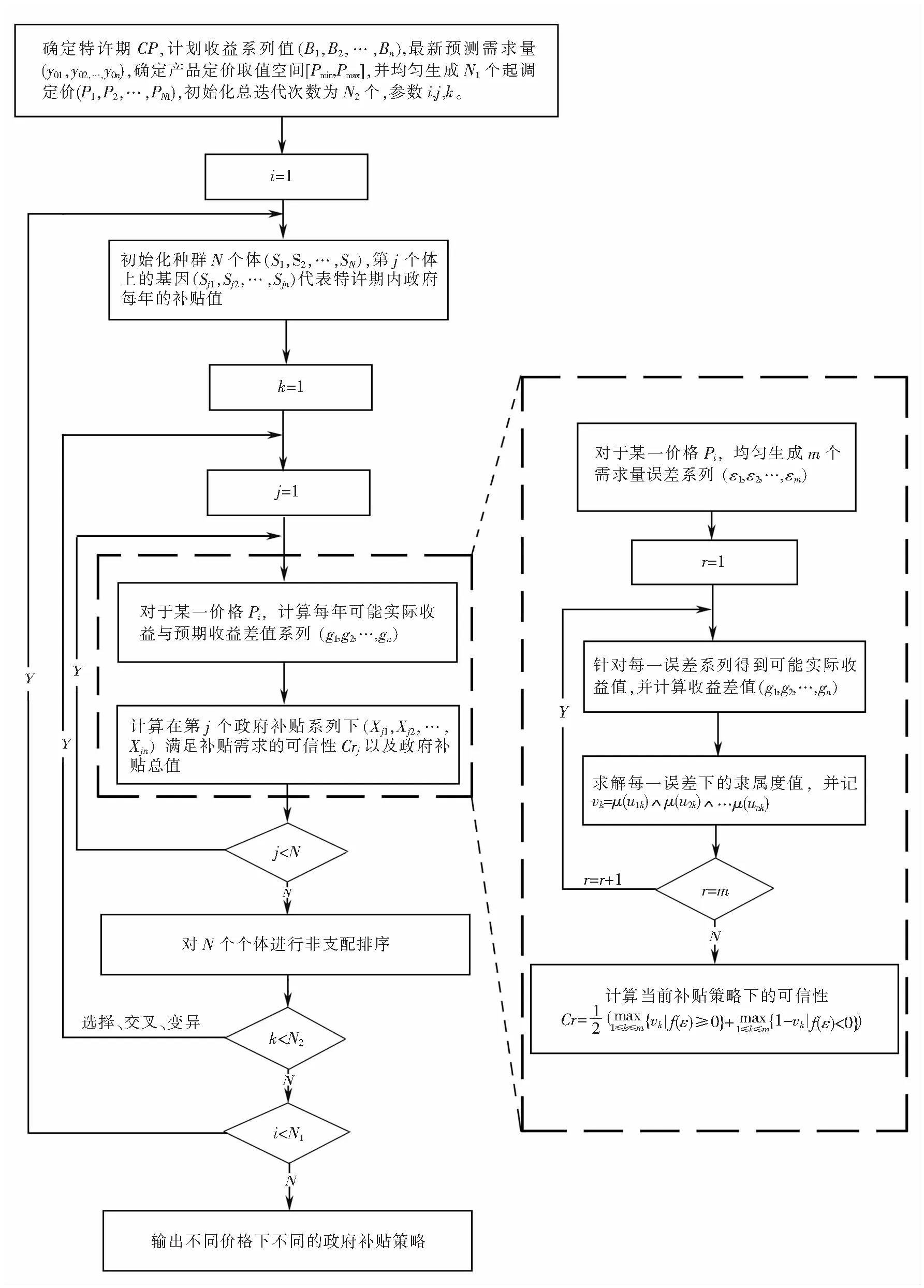
图2 不同定价策略下担保兑付策略计算流程

4 算例

4.1 案例背景

某污水处理厂以PPP模式建设，基础测算数据如表1所示。

表1 污水处理厂测算基础数据

注：固定成本、变动成本和初始定价均为初始运营年数值，资金时间价值参考三年期国债利率。

由于项目实际需求量的不确定性，投产后1～3年期间实际收益低于最低担保收益，期间的实际需求量和计划需求量数据如表2所示。

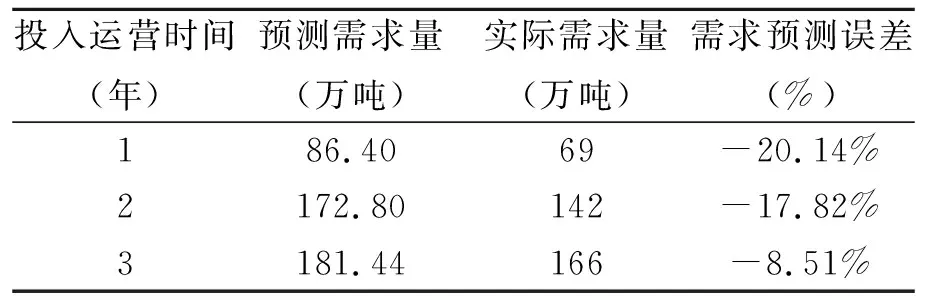
表2 污水处理厂需求量数据

4.2 结果分析

在此以第三年年末时点数为例，对模型应用进行验证。本文选取柯西分布作为需求预测误差的隶属度函数[23]，结合历史数据采用数理统计方法得到其函数形式及参数，如表3所示。

表3 柯西分布函数形式及其参数

求解得到不同起调价格下政府担保兑付策略非劣解集后，选择具有典型性的策略，通过图表直观反映第4年起调价格(P4)、兑付额年序列现值总额(Stotal)和可信性(Cr)的关系，如图3所示。

图3 起调价格-预测兑付额年序列现值总额-可信性

由图3易知，随Stotal或P4的增加，Cr也随之增加；在既定Cr条件下，Stotal和P4存在负相关关系。更进一步，可以看出，在给定P4情况下，当Cr小于0.4时，Stotal的增长变化幅度很小；当Cr位于[0.4,0.9]时，Stotal的增长变化幅度较为明显，但其相对增长幅度小于Cr的相对增长幅度；当Cr大于0.9时，预测Stotal的相对增长幅度显著超过了可信性的相对增长幅度。

更进一步，由于既定P4情况下，任一担保兑付策略都具有唯一的Stotal和Cr，因此，可对P4、Stotal和Cr三者关系展开分析如下：

(1)固定P4，对Stotal和Cr的关系进行分析。以P4为1.15元为例，选择5组不同Cr{1.00,0.90,0.81,0.69,0.50}对应的担保兑付策略进行分析，结果表明，不同Cr对应的预测兑付额年序列变化趋势一致，且Cr越高，变化幅度越趋于稳定。上述5组策略对应的Stotal分别为{2294.98,2169.69,2044.41,1960.89,1821.68 }(单位：万元)，对应的最高预测年兑付额均出现在第13年，分别为{110.88,104.68,98.48,94.35,87.46}(单位：万元)。此时，可认为当Cr为1时，根据可信性遗传算法所求得的非劣策略即为预期应支付的担保兑付年序列的可能上限。

(2)固定Cr，对P4和Stotal的关系进行分析。以Cr为1为例，选择6组不同的P4{1.15,1.20,1.25,1.30,1.35,1.40}(单位：元)，对应的政府担保兑付策略进行分析，结果表明，上述6组策略对应的Stotal分别为{2294.98,2052.57,1809.51,1564.06,1320.77,1078.69}(单位：万元)，对应的最高预测年兑付额均出现在第13年，分别为{110.88, 102.62, 93.66, 85.40, 77.13, 68.87}(单位：万元)。最高预测年兑付额均出现在第13年的原因是，按照计划，第13年计划产量将达到设计产量上限，因此该年的补贴额通常为整个运营期内的最高值。

(3)固定Stotal的约束区间，对P4和Cr的关系进行分析。可筛选出担保兑付策略现值总额相近的不同P4、不同Cr下的政府担保兑付策略集合，例如将筛选条件设置为{Stotal∈[1805,1825],Cr≥0.50,P4≤1.30元}，在此选取有代表性的3组策略，分别为策略1{Stotal=1821.68万元，Cr=0.50，P4=1.15元}， 策略2{Stotal=1824.06万元，Cr=0.80，P4=1.20元}和策略3{Stotal=1809.51万元，Cr=1.00，P4=1.25元}进行分析。结果表明，上述策略中虽然Stotal接近，但P4和Cr存在显著差异，并且各策略预测兑付额年序列的趋势和调整幅度存在一定差异，Cr较高的策略2和策略3的预测兑付额年序列相似度更高，而Cr较低的策略1在第21年至第27年期间的两个调价周期内，与策略2和策略3的预测兑付额年序列变化趋势出现了明显背离。

5 结论与启示

本文针对需求不足情形下由于最小收益担保引起的财政担保兑付策略问题进行了研究。将表征预算资金使用效率的预测兑付额年序列现值总额以及表征违约风险的担保兑现保证率作为多目标函数，建立考虑需求预测误差的PPP项目多目标担保兑付模型；考虑到收益和或有债务测算过程中需求不确定性具有一定的模糊性特征，通过引入模糊数学可信性理论，对担保合同兑现保证率进行量化，并提出了基于可信性遗传算法对模型进行求解。结合案例分析对模型应用进行了验证，对各种既定条件下的政府担保兑付策略进行了求解和分析。结果表明，当可信性位于[0.9,1]区间内时，预测兑付额年序列现值总额对保证率变动的敏感性最高，因此，可考虑将担保合同兑现保证率设置为[0.8,0.9]区间，能够在保证相对较高的担保兑付保证率的同时，有效提高财政预算资金的使用效率。实践中，针对同一区域内普遍存在多个PPP项目担保的情况，可根据项目的实际情况，在对消费者承受能力进行评估的基础上，结合价格调整策略，分别对不同PPP项目的担保合同兑现保证率的约束区间进行设置，从而更好地实现财政授权支付额度的合理安排。综上，考虑需求预测误差的PPP项目多目标担保兑付模型和可信性遗传算法的提出能够为实践中地方财政预算紧张、而预期财政或有债务又需保证偿付的多目标问题提供科学有效的量化决策依据，进而有效提升财政预算资金的使用效率和政府方的财政风险管控能力，对PPP项目的良性发展有着重要意义。